基于电机双轴加载的中小型隧道物理模拟试验系统研制与应用

李元海; 刘德柱; 杨硕

doi:10.11779/CJGE202008022

基于电机双轴加载的中小型隧道物理模拟试验系统研制与应用 English Version

李元海^{1, 2,},
刘德柱²,
杨硕¹

1.
中国矿业大学深部岩土力学与地下工程国家重点实验室江苏　徐州　221116
2.
中国矿业大学力学与土木工程学院,江苏　徐州　221116

基金项目:

国家重点基础研究发展计划（“973”计划）项目 2016CB46905

国家自然科学基金项目 51174197

详细信息

作者简介:
李元海(1969—),男,博士,教授,主要从事岩土工程数字照相量测技术与应用以及地下工程安全分析与稳定性控制机理等方面的研究工作。E-mail：lyh@cumt.edu.cn

中图分类号: TU457
计量
- 文章访问数: 266
- HTML全文浏览量: 10
- PDF下载量: 114
出版历程
- 收稿日期: 2019-10-30
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-07-31

Development and application of physical simulation test system for small and medium-sized tunnels based on biaxial motor loading

1.
State Key Laboratory for Geomechanics & Deep Underground Engineering, Xuzhou 221116, China
2.
School of Mechanics & Civil Engineering, China University of Mining and Technology, Xuzhou 221116, China

摘要

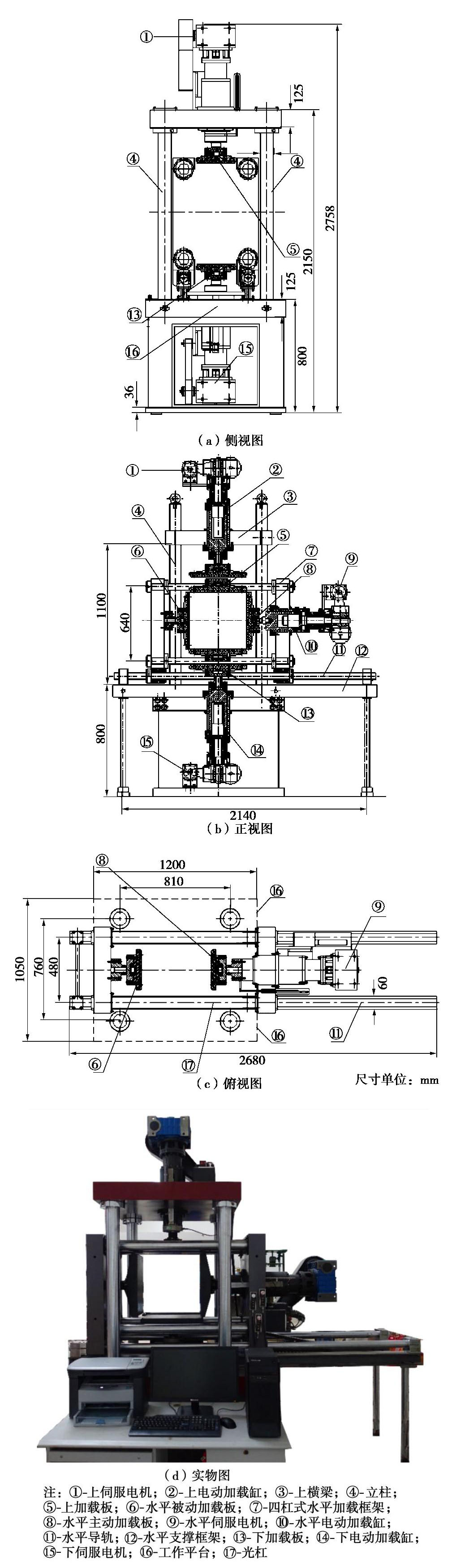
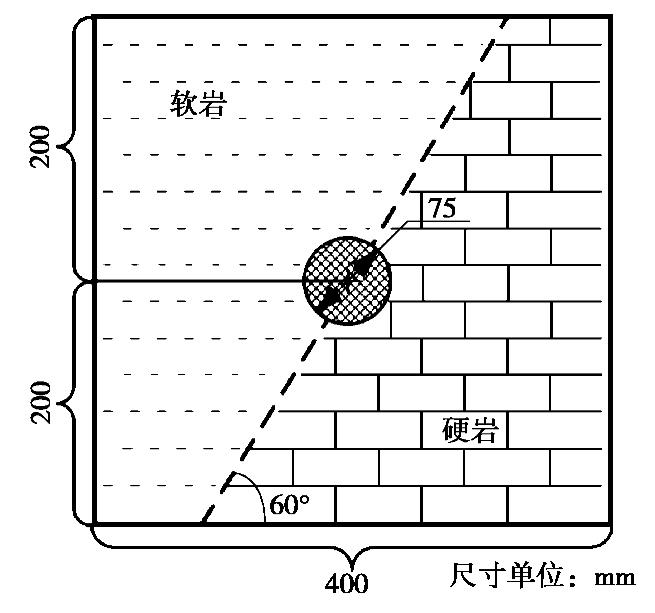
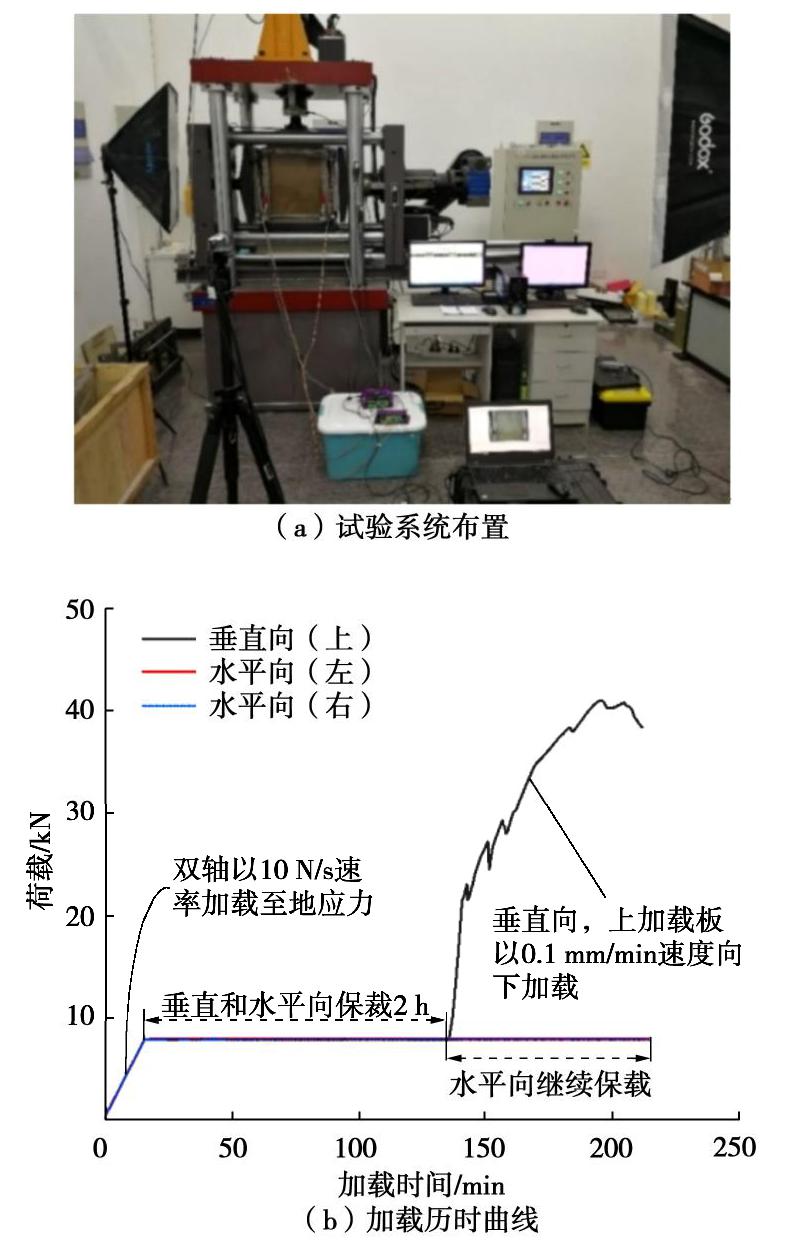
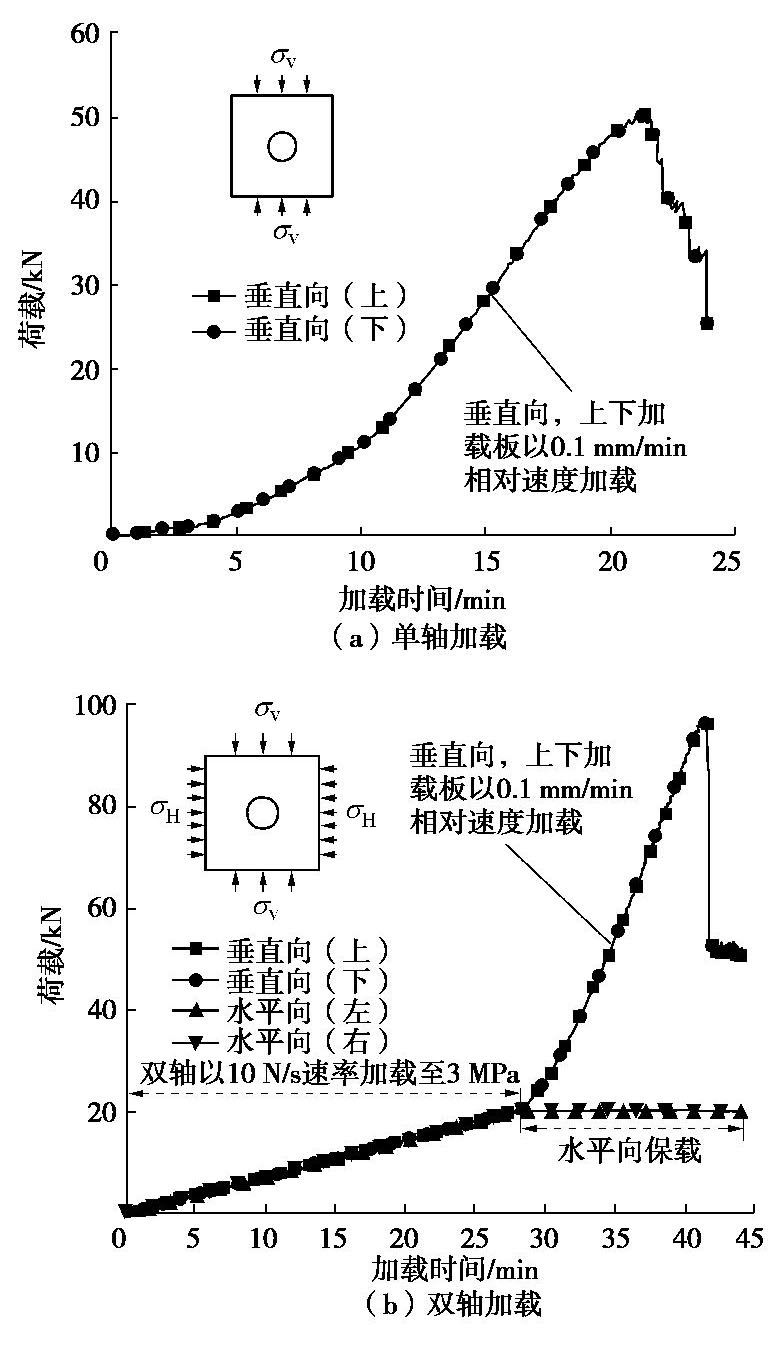
摘要: 为研究深部隧道围岩变形破裂过程及演化机理问题,并针对当前隧道工程试验系统中存在的关键问题,研制了一套结构紧凑、模型尺寸适中、稳压效果良好的双轴电机加载物理模拟试验系统。该系统由框架式反力架、伺服电机加载及控制系统、自行研制的数字照相变形量测系统和开挖辅助装置等部分组成,不仅可以用于中小型隧道物理模拟试验,还可完成普通相似材料的标准或非标准试件的单轴与双轴压缩试验研究等。最后给出类岩石材料单、双轴压缩试验及复合地层相似材料围岩变形破裂试验的应用实例,部分试验结果与类似研究成果基本一致,表明本套试验系统能够满足隧道围岩稳定性等问题研究的需要,同时,试验结果可为相关问题研究提供参考。
- 隧道 /
- 双轴加载 /
- 相似模拟 /
- 模型试验 /
- 数字照相量测
Abstract: To study the failure process of deformation and evolution mechanism of the surrounding rock in deep tunnels, as well as to solve the key problems of the current tunneling test system, a new motor biaxial loading system with compact structure, moderate size and stabilized loading is developed for simulating physical tunnels. The system consists mainly of a frame-type reaction frame, a servo-controlled motor testing system, a self-developed digital photographic deformation measurement system and auxiliary devices for excavation. It can be used for the physical simulation tests on small and medium-sized tunnels and the uniaxial and biaxial compression tests on standard or non-standard specimens made of the common similar materials. Finally, the uniaxial and biaxial compression tests on the rock-like specimens and the simulation experiments to study the deformation evolution of the surrounding rock in mixed strata are performed to verify the feasibility of the test system. Partial experimental results are basically consistent with those of the similar studies, which indicates that the poposed test system meets the needs of studying the stability of the surrounding rock and other issues. Furthermore, the results may also provide reference for the related researches.
- tunnel /
- biaxial loading /
- similar simulation /
- model test /
- digital photogrammetry

HTML全文

0. 引言

随着中国城市化进程的快速推进以及交通运输网络规模的不断扩大,近年来隧道工程建设量大、面广。由于受地质条件、施工技术、使用功能等诸多因素影响,隧道横断面的形状设计复杂多变。例如,宁波地铁4号线工程中采用的类矩形盾构隧道^[1],岩石地层中采用钻爆法施工的直墙拱形隧道^[2]。然而,近年来地下结构震害频发,与圆形隧道相比,非圆隧道由于形状曲率变化导致其地震响应更为复杂。因此,研究非圆等任意断面形状隧道的地震响应,对于指导实际工程抗震设计具有广泛意义。

目前,隧道结构的地震响应分析主要采用数值模拟或模型试验。Amorosi等^[3]建立二维有限单元模型研究了黏性土中浅埋隧道的动力响应；Stamos等^[4]采用频域边界元法求解了三维地下结构的动力响应；Yu等^[5-7]采用多尺度方法分析了长隧道在一致和非一致地震作用下的动力响应规律；袁勇等^[8-9]、禹海涛等^[10]基于多台面振动台模型试验,研究了长大隧道在非一致激励下的地震响应机制。由于数值方法建模工作量大,且计算精度受参数取值影响,而模型试验受台面限制且周期长,因此实际工程设计通常采用拟静力法等简化方法。

深埋隧道的拟静力方法是将地震作用简化为远场剪应力或剪应变,基于简化模型进行静力分析计算^[11]。Bobet^[12]研究表明,当地震的波长大于隧道尺寸的8倍时,地震荷载可简化为准静态荷载,而实际工程中大部分隧道均满足此条件。拟静力法通常分为自由场变形法和地层–结构相互作用法。前者将地震引起的地层变形直接施加在结构上,由于忽略了地层–结构相互作用,因而得到的地震响应往往误差较大；后者合理考虑了地层与结构之间的相互作用关系,故得到的结果更接近实际情况,而且基于该方法的解析解具有计算简便、参数少、耗时少等优点,备受工程设计人员所青睐。如对于圆形隧道,Wang^[13]基于Einstein^[14]等提出的相对刚度法给出了圆形隧道在远场剪应力作用下的最大内力与变形；Penzien等^[15]通过假设地层与结构接触面的应力分布推导出另一个不同形式的解答；Bobet等^[12,16]拓展研究了饱和地层隧道在衬砌界面排水与不排水条件下的地震响应。对于矩形隧道,Penzien^[17]通过忽略了地层与隧道接触面上的法向应力,并基于圆形隧道的变形假设给出了近似解；Huo等^[18]应用复变函数方法,考虑了地层–结构接触面上应力和位移的连续性条件,推导出更为精确的解答。然而,以上基于地层–结构相互作用拟静力方法推导出的解析解,只适用于圆形或矩形等简单形状隧道,尚缺少面向更广泛工程设计的任意断面形状深埋隧道地震响应的解析解。

本文基于地层–结构相互作用的拟静力方法,建立了任意形状深埋隧道横向地震响应分析模型,综合考虑了隧道内部中隔墙的影响,以及地层–结构交界面上不滑移和全滑移两种典型接触条件,采用复变函数与保角映射法,推导出任意形状深埋隧道地震响应的解析解。以有限元数值解为基准,验证了本文方法的有效性和可行性。在此基础上,应用该解析方法分析了地层–结构相对刚度比、地层–结构接触条件、中隔墙刚度等因素对深埋隧道地震响应的影响规律。

1. 模型与假定

本文针对在远场剪应力作用下具有任意形状横断面的隧道结构,计算模型和坐标系统如图1所示。τ为远场剪应力,隧道的对称轴为x轴,L₁为地层与衬砌的接触面,φ为衬砌任一位置点关于x轴的夹角,δ为衬砌厚度。记地层的弹性模量和泊松比为E_g和 $ν_{g}$ ,衬砌的弹性模量和泊松比为E_l和 $ν_{l}$ 。

图 1 远场剪应力作用下的任意形状深埋隧道

Figure 1. Deep tunnel with arbitrary cross-section shapes subjected to far-field shear loading

下载: 全尺寸图片幻灯片

计算分析时的简化假定如下：①地层与衬砌为各向同性线弹性体。②地层与衬砌各处的纵向应变为0,即满足平面应变条件。③隧道横断面具有一个对称轴。④隧道埋深较大,在地震作用下处于远场剪应力状态。剪应力大小为^[15]

$τ = 0.5 E_{g} V_{\max} / [V_{S} (1 + ν_{g})]$ 。

(1)

式中 $V_{\max}$ 为地震动的峰值速度； $V_{S}$ 为场地剪切波速。⑤衬砌的厚度与隧道横断面尺寸相比可以忽略,衬砌假定为壳体,衬砌变形时满足平截面假定。

2. 解析解推导

2.1 保角变换

对于横断面形状比较复杂的隧道,可以使用保角变换将Oxy平面内的隧道映射成 $ζ$ 平面上的单位圆 $Θ = e^{i θ}$ 来分析,如图2所示。保角映射的形式为^[19]

$z = ω (ζ) = R (ζ + \sum_{k = 0}^{n} C_{k} ζ^{- k})$ 。

(2)

图 2 保角变换

Figure 2. Conformal transformation

下载: 全尺寸图片幻灯片

式中 z为oxy平面上一点,z=x+iy；R和C_k为实常数,可通过复合形方法等优化算法由隧道的尺寸和形状确定^[20]。对于任意形状的隧道,都可以获得精度很高的映射函数。由于衬砌采用壳体假设,映射后衬砌的厚度不发生变化。

2.2 地层的应力与位移

根据弹性理论,地层的应力与位移可以由两个复势函数φ(z)和ψ(z)来表示^[21]：

$\begin{array}{l} σ_{x}^{g} + σ_{y}^{g} = 4 Re [φ^{'} (z)], \\ σ_{x}^{g} - σ_{y}^{g} + 2 i τ_{x y}^{g} = 2 [\bar{z} φ^{″} (z) + ψ^{'} (z)], \\ 2 G_{g} (u_{x}^{g} + i u_{y}^{g}) = (3 - 4 ν_{g}) φ (z) - z \bar{φ^{'} (z)} - \bar{ψ (z)} 。 \end{array}}$

(3)

式中, $σ_{x}^{g}$ , $σ_{y}^{g}$ 和 $τ_{x y}^{g}$ 为地层中任一点在oxy坐标系下的应力分量, $u_{x}^{g}$ 和 $u_{y}^{g}$ 为地层中任一点在oxy坐标系下的位移分量, $G_{g}$ 为地层的剪切模量。

地层受远场剪应力τ作用,设由地层–结构相互作用引起的地层位移在无穷远处为0,则地层的复势函数为^[19]

$\begin{array}{l} φ (ω (ζ)) = i φ_{1} (ζ) = i \sum_{k = 1}^{\infty} a_{k} ζ^{- k}, \\ ψ (ω (ζ)) = i τ ω (ζ) + i ψ_{1} (ζ) = i τ ω (ζ) + i \sum_{k = 1}^{\infty} b_{k} ζ^{- k} 。 \end{array}}$

(4)

式中, $a_{k}$ 和 $b_{k}$ 为实数,i为虚数单位。为了简化分析,在计算中只考虑级数中的前N项,并记

$\begin{matrix} X_{k} = a_{k}, & X_{N + k} = b_{k} & (k = 1, 2, \dots, N \end{matrix})$ 。

(5)

将式（4）代入式（3）中,并结合转轴公式^[20]和复合函数的求导法则,可解得 ${ρ, θ}$ 坐标系中开挖面上地层的应力与位移：

$\begin{array}{l} σ_{ρ}^{g} = - 2 Im [{φ^{'}}_{1} (Θ) / ω^{'} (Θ)] + \\ Im {σ^{2} [ω (1 / Θ) {φ^{″}}_{1} (Θ) - ω (1 / Θ) ω^{″} (Θ) {φ^{'}}_{1} (Θ) / ω^{'} (Θ) + \\ ω^{'} (Θ) {ψ^{'}}_{1} (Θ) + τ ω^{'} (Θ) ω^{'} (Θ)]} / ω^{'} (1 / Θ) ω^{'} (Θ), \end{array}$

(6a)

$\begin{array}{l} τ_{ρ θ}^{g} = 1 / ω^{'} (1 / Θ) ω^{'} (Θ) Re {Θ^{2} [ω (1 / Θ) {φ^{″}}_{1} (Θ) - \\ ω (1 / Θ) ω^{″} (Θ) {φ^{'}}_{1} (Θ) / ω^{'} (Θ) + \\ ω^{'} (Θ) {ψ^{'}}_{1} (Θ) + τ ω^{'} (Θ) ω^{'} (Θ)]}, \end{array}$

(6b)

$\begin{array}{l} u_{ρ}^{g} = - 1 / 2 G_{g} | ω^{'} (Θ) | Im {Θ^{- 1} [κ_{g} ω^{'} (1 / Θ) φ_{1} (Θ) + \\ ω (Θ) {φ^{'}}_{1} (1 / Θ) + ω^{'} (1 / Θ) ψ_{1} (1 / Θ) - τ ω^{'} (1 / Θ) ω (1 / Θ)]}, \end{array}$

(6c)

$\begin{matrix} u_{θ}^{g} = 1 / (2 G_{g} | ω^{'} (Θ) |) Re {Θ^{- 1} [κ_{g} ω^{'} (1 / Θ) φ_{1} (Θ) + \\ ω (Θ) {φ^{'}}_{1} (1 / Θ) + ω^{'} (1 / Θ) ψ_{1} (1 / Θ)] - τ ω^{'} (1 / Θ) ω (1 / Θ)} 。 \end{matrix}$

(6d)

式中,各项均为关于 $Θ$ 的Laurent级数,因而将式（2）,（5）代入式（6a）～（6d）中,通过级数运算可以将开挖面上地层的应力与位移表示成如下形式：

$σ_{ρ}^{g}, u_{ρ}^{g}, τ_{ρ θ}^{g}, u_{θ}^{g} ~ \sum_{k = - p_{k}^{(l)}}^{p_{k}^{(l)}} \sum_{j = 1}^{2 N} U_{k j}^{(l)} X_{j} Θ^{k} + \sum_{k = - p_{k}^{(l)}}^{p_{k}^{(l)}} V_{k}^{(l)} Θ^{k}$ ,

(7)

式中,应力与位移的Laurent系数为 $X_{k}$ 的线性组合, $U_{k j}^{(l)}$ 为k阶Laurent级数项中 $X_{j}$ 的系数, $V_{k}^{(l)}$ 为常数。

2.3 衬砌的控制方程

根据壳体理论^[19],衬砌上任一点的轴力T与弯矩M可以表示为

$\begin{array}{l} T = \frac{E_{l} δ}{1 - ν_{l}^{2}} (\frac{d u_{θ}^{l}}{d s} + K u_{ρ}^{l}), \\ M = - \frac{E_{l} δ^{3}}{12 (1 - ν_{l}^{2})} [\frac{d^{2} u_{ρ}^{l}}{d s^{2}} + K^{2} u_{ρ}^{l} - \frac{d K}{d s} u_{θ}^{l}] 。 \end{array}}$

(8)

式中 T和M分别为衬砌任意位置上的轴力与弯矩； $u_{θ}^{l}$ , $u_{ρ}^{l}$ 为 ${ρ, θ}$ 坐标系下的衬砌位移；s为L₁的线长参数；K为衬砌上任一点的曲率,向外弯为正。衬砌的平衡方程为

$\begin{array}{l} d T /d s + K d M /d s + τ_{ρ θ}^{l} = 0, \\ - K T + d^{2} M /d s^{2} + σ_{ρ}^{l} = 0 。 \end{array}}$

(9)

式中, $σ_{ρ}^{l}$ 和 $σ_{ρ}^{l}$ 为 ${ρ, θ}$ 坐标系下的衬砌应力。

将式（8）代入式（9）,有

$\begin{array}{l} d^{2} u_{θ}^{l} /d s^{2} +d (K u_{ρ}^{l}) /d s - K δ^{2} / 12 [d^{3} u_{ρ}^{l} / d s^{3} + \\ d (K^{2} u_{ρ}^{l}) / d s - d (K^{'} u_{θ}^{l}) / d s] = - (1 - ν_{l}^{2}) / (E_{l} δ) τ_{ρ θ}^{l}, \\ K d u_{θ}^{l} / d s + K^{2} u_{ρ}^{l} + δ^{2} / 12 [d^{4} u_{ρ}^{l} /d s^{4} + d^{2} (K^{2} u_{ρ}^{l}) / d s^{2} - \\ d^{2} (K^{'} u_{θ}^{l}) / d s^{2}] = (1 - ν_{l}^{2}) / (E_{l} δ) σ_{ρ}^{l} 。 \end{array}}$

(10)

为了将衬砌在坐标系 ${ρ, θ}$ 中表出,需将式（10）中的各物理量表示为 $Θ$ 的级数。由求导法则,有

$\frac{d}{d s} = \frac{d θ}{d s} \frac{d Θ}{d θ} \frac{d}{d Θ} = \frac{i}{A} \frac{d}{d Θ}$ ,

(11)

式中, $A$ 为曲线的拉梅常数, $A = | ω^{'} (σ) |$ 。 $1 / A$ 和K的表达式可以由式（2）确定,然后将其展开成傅里叶级数。

2.4 边界条件

本文考虑两种典型的地层–结构接触条件：不滑移和全滑移。地层与衬砌不产生相对位移时,应力与位移在接触面上满足连续性条件：

$\begin{array}{l} u_{ρ}^{l} = u_{ρ}^{g}, u_{θ}^{l} = u_{θ}^{g}, \\ σ_{ρ}^{l} = σ_{ρ}^{g}, τ_{ρ θ}^{l} = τ_{ρ θ}^{g} 。 \end{array}}$

(12)

地层–结构间完全滑移时,在接触面上法向应力与法向位移满足连续性条件,切向应力为0,因而有

$\begin{array}{l} u_{ρ}^{l} = u_{ρ}^{g}, \\ σ_{ρ}^{l} = σ_{ρ}^{g} τ_{ρ θ}^{l} = τ_{ρ θ}^{g} = 0 。 \end{array}}$

(13)

需要说明的是,由于深埋隧道受周围岩土体初始自重应力场的作用,即使在地震作用下,衬砌与地层通常不会沿接触面法向脱开,因此可视为接触面上法向应力与法向位移保持连续。

2.5 求解步骤

首先求解地层–结构间不滑移的解,将式（7）,（12）代入式（10）中,并结合式（11）,有

$\begin{array}{l} \sum_{k = M_{1}}^{M_{1}} \sum_{j = 1}^{2 N} {(F_{1})}_{k j} X_{j} Θ^{k} = \sum_{k = M_{1}}^{M_{1}} {(b_{1})}_{k} Θ^{k}, \\ \sum_{k = M_{2}}^{M_{2}} \sum_{j = 1}^{2 N} {(i F_{2})}_{k j} X_{j} Θ^{k} = \sum_{k = M_{2}}^{M_{2}} {(i b_{2})}_{k} Θ^{k} 。 \end{array}}$

(14)

通过比较式（14）等式两边同幂项的系数,可以获得一组线性方程,则待定系数 $x_{k}$ 可以通过求解这个线性方程组得到。

地层–结构间完全滑移时,将衬砌切向位移作傅里叶级数展开,有

$u_{θ}^{l} = \sum_{k = 0}^{N} d_{k} \cos k θ = \frac{1}{2} \sum_{k = 0}^{N} d_{k} (Θ^{k} + Θ^{- k})$ ,

(15)

并记

$X_{2 N + k} = d_{k} (k = 1, 2, 3, \dots, N + 1)$ 。

(16)

将（7）,（13）,（15）代入式（10）中,并结合式（11）,得

$\begin{matrix} \sum_{j = 1}^{3 N + 1} {(F_{3})}_{k j} X_{j} {(b_{3})}_{k} & (k = 0, 1, 2, 3, \dots, N), \\ \sum_{j = 1}^{3 N + 1} {(F_{4})}_{k j} X_{j} {(b_{4})}_{k} & (k = 1, 2, 3, \dots, N), \\ \sum_{j = 1}^{2 N} U_{k j}^{(3)} X_{j} = - V_{k}^{(3)} & (k = 0, 1, 2, 3, \dots, N) 。 \end{matrix}}$

(17)

同样的,通过比较式（7）等式两边同幂项的系数,可以解出所有的待定参数。

具体求解流程归纳如下：①通过式（6）计算式（7）中各参数；②将式（7）代入式（10）,依据不同的接触条件,计算式（14）或式（17）中各参数；③求解式（14）或式（17）,得出待定系数 $X_{k}$ 和 $d_{k}$ ；④将 $x_{k}$ 代入式（7）,得开挖面上地层的应力与位移；⑤地层–结构不滑移时,由式（12）确定衬砌的应力与位移。地层–结构全滑移时,将 $d_{k}$ 代入式（15）得到衬砌的切向位移,再由式（13）得到其余的衬砌应力和位移,地层与衬砌在oxy坐标下的应力与位移可由式（3）,（4）求得；⑥将衬砌的应力和位移代入式（8）,得到衬砌的轴力与弯矩。

2.6 含中隔墙隧道的解答

在远场剪应力的作用下,中隔墙对隧道管片作用为剪力T和弯矩 $M_{1}$ 和 $M_{2}$ ,如图3所示。

图 3 含中隔墙隧道计算简图

Figure 3. Mechanical model for a tunnel with middle wall

下载: 全尺寸图片幻灯片

为了计算集中力（矩）作用在衬砌内部时的响应,使用如下函数来描述集中力（矩）：

$f (θ) = {\begin{matrix} {[ε + \cos k_{a} θ]}^{k_{b}} & (| θ | \leq 10 \sqrt{ε} / k_{a}) \\ 0 & (其它) \end{matrix}$ ,

(18)

式中, $ε = 10^{- 4}$ , $k_{a} = 5$ , $k_{b} = 10^{3}$ , $f (θ)$ 为仅在 $θ = 0$ 附近不为0的函数。

记中隔墙端部剪力为 $T A_{1} f (θ) + T A_{2} f (θ + π)$ ,力矩为 $M_{1} A_{1} f (θ) + M_{2} A_{2} f (θ + π)$ , $A_{1}$ 和 $A_{2}$ 为实参数,由归一化条件确定。

则 $T$ , $M_{1}$ 和 $M_{2}$ 与衬砌位移有如下关系：

$\begin{array}{l} (1 - ν_{l}^{2}) T = 6 i / l [d u_{ρ}^{l} / d s (0) + d u_{ρ}^{l} /d s (π)] + \\ 12 i / l^{2} [u_{θ}^{l} (0) + u_{θ}^{l} (π)], \\ (1 - ν_{l}^{2}) M_{1} = - i [4 d u_{ρ}^{l} /d s (0) + 2 d u_{ρ}^{l} /d s (π)]] + \\ 6 i / l^{2} [u_{θ}^{l} (0) + u_{θ}^{l} (π)], \\ (1 - ν_{l}^{2}) M_{2} = i [2 d u_{ρ}^{l} /d s (0) + 4 d u_{ρ}^{l} /d s (π)] + \\ 6 i / l^{2} [u_{θ}^{l} (0) + u_{θ}^{l} (π)] 。 \end{array}}$

(19)

式中, $i = E I_{m} / l$ , $I_{m}$ 为中隔墙单位纵截面的转动惯量,l为中隔墙长度, $I_{m} = δ_{m}^{3} / 12$ , $δ_{m}$ 为中隔墙厚度。忽略剪力对衬砌管片法向平衡的影响,则中隔墙对衬砌管片的作用可以由如下应力分布表示：

$\begin{matrix} σ_{ρ 0}^{1} = - M_{0} d^{2} f (θ) / d s^{2}, \\ τ_{ρ θ 0}^{1} = - T_{0} d f (θ) / d s - M_{0} K d f (θ) / d s 。 \end{matrix}}$

(20)

将式（9）改为如下形式：

$\begin{array}{l} d T / d s + K d M /d s + τ_{ρ θ}^{l} + τ_{ρ θ 0}^{l} = 0, \\ - K T + d^{2} M /d s^{2} + σ_{ρ}^{l} + σ_{ρ 0}^{l} = 0 。 \end{array}}$

(21)

按照2.5节的计算步骤,在步骤③中联立式（19）,可求得衬砌与地层的应力和位移。

3. 数值验证

建立有限元基准模型来验证本文解析方法的有效性和可行性。选用如下两种不同形状的隧道进行对比验证：不含中隔墙的直墙拱形隧道^[21]和含中隔墙的类矩形隧道^[1]。隧道设防烈度设为Ⅶ,地震动峰值速度 $V_{\max} = 0.13 m/s$ ^[22]。

假设直墙拱形隧道高6 m,宽4.85 m,衬砌厚度 $δ$ 为0.3 m,弹性模量 $E_{l}$ 为30 GPa,泊松比 $ν_{l}$ 为0.2。地层弹性模量 $E_{g}$ 为5 GPa,泊松比 $ν_{g}$ 为0.25,场地剪切波速 $V_{\max} = 800 m/s$ 。

$\begin{matrix} z = ω (ζ) = 3 (ζ - 0.1036 + 0.0873 ζ^{- 1} + 0.0729 ζ^{- 2} - \\ 0.0984 ζ^{- 3} + 0.0384 ζ^{- 4} + 0.0052 ζ^{- 5}) \end{matrix}$ 。

(22)

类矩形隧道高6.49 m,宽11.05 m,衬砌厚度 $δ$ 为0.45 m,中隔墙厚度 $δ_{m}$ 为0.35 m,衬砌弹性模量 $E_{l}$ 为34.5 GPa,泊松比 $ν_{l}$ 为0.2。地层弹性模量 $E_{g}$ 为1 GPa,泊松比 $ν_{g}$ 为0.25,场地剪切波速 $V_{\max} = 200 m/s$ 。隧道映射函数如下：

$\begin{matrix} z = ω (ζ) = 4 .4434(ζ - 0.26173 ζ^{- 1} - 0.0145 ζ^{- 3} + \\ 0.00635 ζ^{- 5} + 0.00193 ζ^{- 7} - 0.00136 ζ^{- 9}) \end{matrix}$ 。

(23)

基于大型通用软件ABAQUS建立相应的有限元模型,采用梁单元模拟衬砌结构,平面应变单元模拟地层。地层–结构间不滑移时,采用绑定约束；地层–结构间全滑移时,法向为硬接触,切向设为Coulomb型接触面。衬砌内边界的切向正应力为 $σ_{θ} = T / δ +$ $M δ / 2 I$ ,式中, $I = δ^{3} / 12$ 。

图4给出了直墙拱形隧道衬砌内边界上归一化切向正应力 $σ_{θ} / τ$ 的分布情况,图5给出了不滑移条件下类矩形隧道中 $σ_{θ} / τ$ 的分布情况,以及考虑初始地应力条件（竖向应力 $σ_{v} = 900 kPa$ ,水平应力 $σ_{h} =$ $630 kPa$ ）时地层–结构交界面上的法向接触应力 $σ_{ρ}$ 分布。根据算例中隧道结构的对称性,取1/2模型进行地震响应分析。

图 4 直墙拱形隧道地震响应对比验证

Figure 4. Comparison of seismic responses of straight-wall-arch shaped tunnel by FEM model and proposed analytical solution

下载: 全尺寸图片幻灯片

图 5 类矩形隧道地震响应对比验证

Figure 5. Comparison of seismic responses of quasi-rectangular tunnel by FEM model and proposed analytical solution

下载: 全尺寸图片幻灯片

对比本文解析解与有限元数值解可以看出,分析结果均吻合较好,从而验证了本文解析解的正确性。此外,解析解与数值解均表明地震作用下隧道-地层接触面法向接触应力总为压应力,进一步说明了地层与结构沿法向不会脱开,也即交界面上的法向应力和法向位移保持连续性。

4. 参数敏感性分析

在以上验证算例的基础上,选取了地层–结构相对刚度比和中隔墙厚度进行参数敏感性分析,并研究了隧道形状和地层–结构接触条件对隧道地震响应的影响程度。

4.1 地层–结构相对刚度比的影响

在基于相对刚度法的圆形隧道解析解中,引入了压缩比和柔度比来描述地层–结构相对刚度,其中柔度比被认为对地震响应有较大影响^[13]。参照圆形隧道^[12,16],定义非圆隧道的柔度比如下：

$F = \frac{E_{g} R^{3} (1 - ν_{l}^{2})}{E_{l} I (1 - ν_{g}^{2})}$ 。

(24)

图6给出了直墙拱形隧道衬砌内边界上归一化切向正应力的最大值与柔度比的关系,以及归一化法向位移最大值 $u_{ρ}^{l} / u_{free field} = 2 G u_{ρ}^{l} / τ R$ 与柔度比的关系, $u_{free field}$ 为与O点距离R处的自由场位移。可见随着柔度比增大,隧道的应力响应减小。当柔度比较小时,即对于软土地层,隧道应力响应随柔度比的增大降低较快,而地层–结构之间的不滑移或全滑移接触边界则对隧道地震响应影响较小。当柔度比较大时,如对于岩石地层,隧道应力响应的最大值对地层–结构相对刚度较不敏感,地层–结构不滑移时的响应略大于全滑移时的响应。隧道的位移响应与内力响应变化规律相反,即随着柔度比的增大而增大,且全滑移条件下的衬砌最大位移大于不滑移条件下的位移。而在衬砌接近刚体即柔度比趋近于0时,位移响应接近于0。

图 6 柔度比对隧道最大内力响应和位移响应的影响

Figure 6. Effects of flexibility ratio on maximum stress and displacement responses of tunnel

下载: 全尺寸图片幻灯片

4.2 中隔墙厚度的影响

通过改变类矩形隧道验证算例中的中隔墙厚度,探究中隔墙厚度对隧道地震响应的影响。图7给出了不同中隔墙厚度下隧道内边界切向应力分布,中隔墙厚度与衬砌管片厚度的比值分别取0,0.5,1.0,1.5,2.0。从中可以看出中隔墙厚度变化对衬砌内力分布的影响局限在中隔墙端部附近,在远离端部处中隔墙的影响可以忽略不计。当厚度比大于1.5时,中隔墙端部处的内力响应超过了不含中隔墙时的最大内力。因此,在含中隔墙隧道的抗震设计中,对于中隔墙厚度相对衬砌管片较大时,应重点关注中隔墙对隧道最大地震响应的放大作用。

图 7 中隔墙厚度对衬砌内力分布的影响

Figure 7. Effects of thickness of the middle wall on stress distribution of lining

下载: 全尺寸图片幻灯片

5. 结论

本文针对目前工程设计对非圆隧道抗震简化分析方法的实际需求,采用复变函数法推导出任意形状深埋隧道地震响应的解析解,并考虑了地层-隧道不滑移与全滑移两种接触条件以及隧道含中隔墙的影响。通过与有限元基准模型的计算结果对比,验证了本文所推导解析解的正确性。本文所提出的解析解可以简便、快速地对具有任意形状横断面的隧道结构进行抗震安全性评估,为实际工程隧道结构抗震设计与分析提供了实用有效的解析方法。

应用该解析解开展了多因素影响分析,结果表明：

（1）地层与结构的柔度比越大,隧道的内力响应越小,而位移响应越大,且相比岩层隧道,土层隧道的地震响应对柔度比的变化更敏感。

（2）相比地层–结构全滑移条件（Full-slip）,地层-结构不滑移条件（No-slip）下隧道衬砌的内力响应较大而位移响应较小。因此,在土层尤其是软土地层修建隧道时,结构设计应重点关注隧道的抗震安全性。

（3）对比有无中隔墙隧道的抗震分析表明,中隔墙对隧道内力的影响仅局限于中隔墙与隧道相接端部附近,且中隔墙厚度越大,中隔墙端部附近的内力响应越大。对于类矩形隧道,当中隔墙厚度超过衬砌厚度的1.5倍时,中隔墙的存在将显著增大了隧道衬砌的最大内力响应,因此隧道抗震设计时应重点考虑中隔墙的影响。

需要说明的是,本文所推导出的解析解仅针对任意截面隧道结构的地震响应特性,该地震响应解析解还需要与初始静力工况计算结果进行组合,从而应用于实际工程指导隧道结构设计。

图 1 试验系统结构设计及实物图

Figure 1. Diagram and photo of testing system

下载: 全尺寸图片幻灯片

图 2 模型箱实物图

Figure 2. Photos of model box

下载: 全尺寸图片幻灯片

图 3 试件模具图

Figure 3. Mold of specimen

下载: 全尺寸图片幻灯片

图 4 隧道掘进装置及开挖示意图

Figure 4. Tunnel-boring machine and schematic of excavation

下载: 全尺寸图片幻灯片

图 5 相似模型试验地层模型图

Figure 5. Formation combination of simulation experiments

下载: 全尺寸图片幻灯片

图 6 模型试验系统布置及加载历时曲线图

Figure 6. Layout of similar model test system and characteristic curves of loading curves

下载: 全尺寸图片幻灯片

图 7 单双轴试验加载历时曲线

Figure 7. Stress-time curves of uniaxial and biaxial compression tests

下载: 全尺寸图片幻灯片

图 8 单轴压缩试件破坏模式与位移矢量图

Figure 8. Failure modes of uniaxial compression and diagram of displacement vector

下载: 全尺寸图片幻灯片

图 9 双轴压缩试件破坏模式与位移矢量图

Figure 9. Failure modes of biaxial compression and diagram of displacement vector

下载: 全尺寸图片幻灯片

表 1 岩石力学参数

Table 1 Mechanical parameters of rock

岩石类型	抗压强度 $σ_{c}$ /MPa	抗拉强度 $σ_{t}$ /MPa	弹性模量E/GPa	泊松比 $ν$	密度 $ρ$ /(kg·m^-3)
软岩	0.20	0.05	0.19	0.29	1452
硬岩	0.58	0.09	0.51	0.26	1529

下载: 导出CSV

表 2 复合地层围岩破坏及分析

Table 2 Analysis of surrounding rock in mix strata

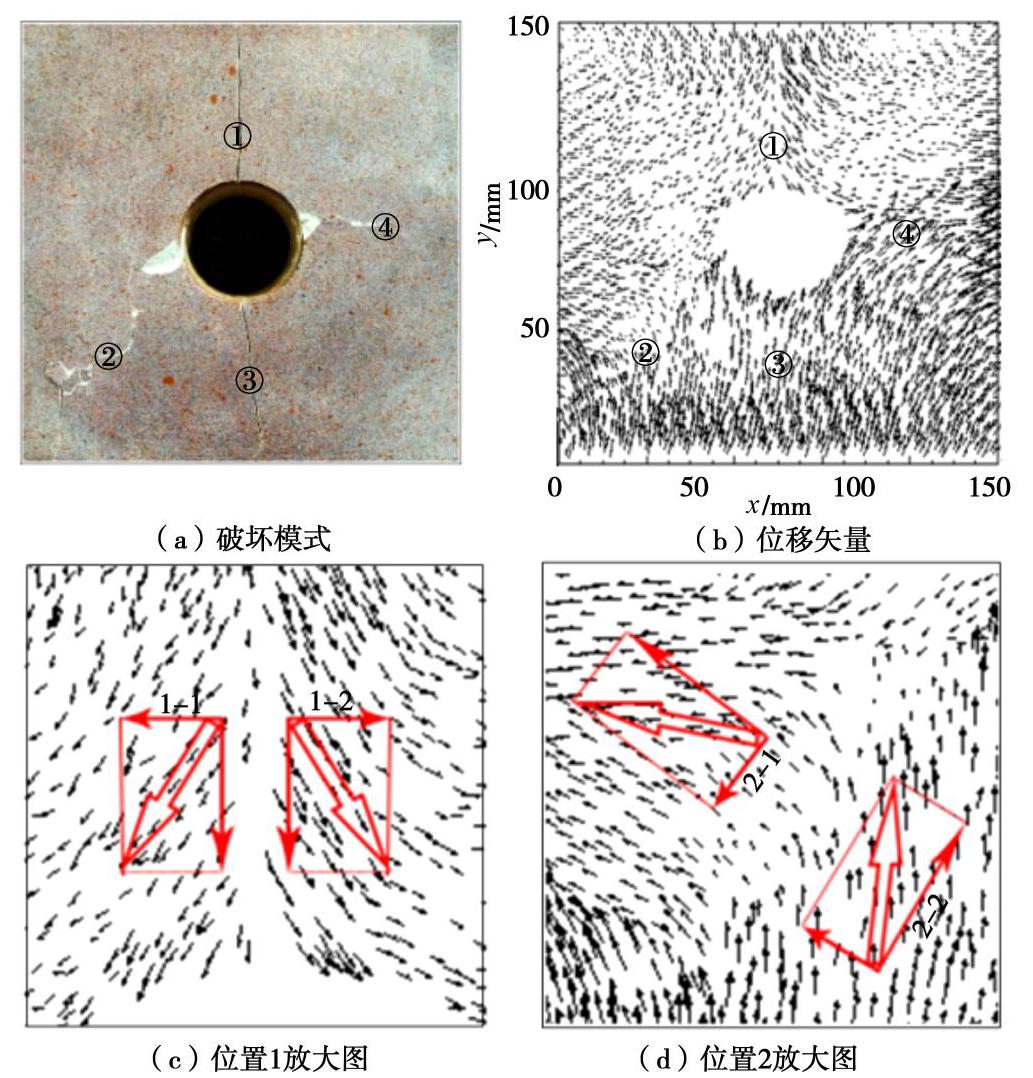
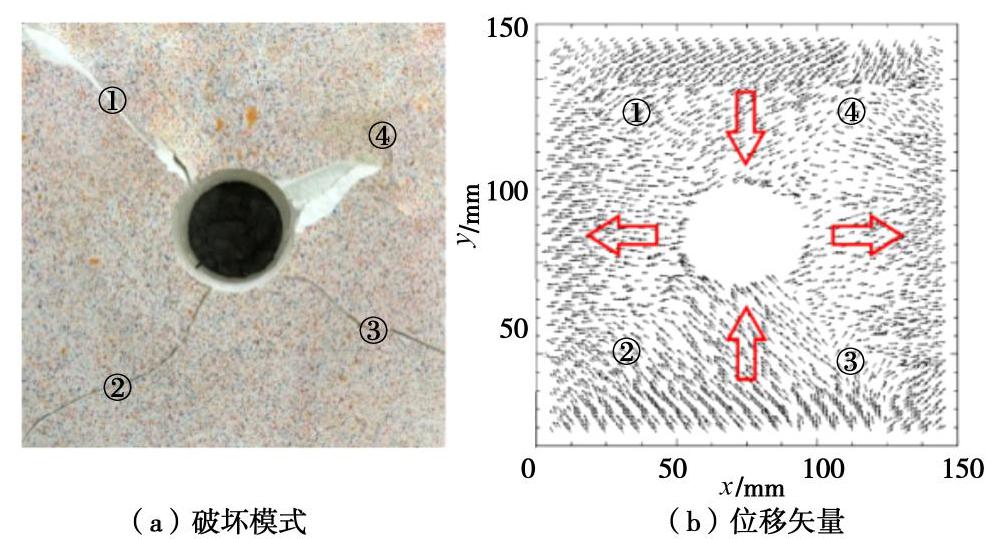
类型	试验过程中	围岩破裂时
围岩图像
位移矢量
位移云图

下载: 导出CSV

表 3 模型材料基本力学参数

Table 3 Basic mechanical parameters of model materials

抗压强度 $σ_{c}$ /MPa	弹性模量E/GPa	泊松比 $ν$	黏聚力c/MPa	内摩擦角ϕ/(°)
7.82	2.16	0.12	2.40	18.4

下载: 导出CSV

表 4 本文试件破坏模式与既有研究对比

Table 4 Comparison of sample failure modes with previous studies

试验	PFC模拟结果^[14]	本文试验结果
单轴压缩
双轴压缩

下载: 导出CSV

参考文献(14)

[1]	李术才, 刘钦, 李利平, 等. 隧道施工过程大比尺模型试验系统的研制及应用[J]. 岩石力学与工程学报, 2011, 30(7): 1368-1374. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201107010.htm LI Shu-cai, LIU Qin, LI Li-ping, et al. Development of large-scale geomechanical model test system for tunnel construction and it's application[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1368-1374. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201107010.htm
[2]	沈泰. 地质力学模型试验技术的进展[J]. 长江科学院院报, 2001, 18(5): 32-36. https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB200105007.htm SHEN Tai. Development of geomechanic model experiment techniques[J]. Journal of Yangtze River Scientific Research Institute, 2001, 18(5): 32-36. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB200105007.htm
[3]	陈安敏, 顾金才, 沈俊, 等. 岩土工程多功能模拟试验装置的研制及应用[J]. 岩石力学与工程学报, 2004, 23(3): 372-378. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200403002.htm CHEN An-min, GU Jin-cai, SHEN Jun, et al. Development and application of multifunctional apparatus for geotechnical engineering model tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(3): 372-378. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200403002.htm
[4]	王汉鹏, 李术才, 郑学芬, 等. 地质力学模型试验新技术研究进展及工程应用[J]. 岩石力学与工程学报, 2009, 28(增刊1): 2765-2771. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2009S1029.htm WANG Han-peng, LI Shu-cai, ZHENG Xue-fen, et al. Geo-mechanical model test new technology research development and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 2765-2771. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2009S1029.htm
[5]	李元海, 杜建明, 刘毅. 隧道工程物理模拟试验技术现状与趋势分析[J]. 隧道建设(中英文), 2018, 38(1): 11-21. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201801002.htm LI Yuan-hai, DU Jian-ming, LIU Yi. The present situation and development trend of physical simulation experiment technology about tunnel engineering[J]. Tunnel Construction, 2018, 38(1): 11-21. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201801002.htm
[6]	张强勇, 陈旭光, 林波, 等. 高地应力真三维加载模型试验系统的研制及其应用[J]. 岩土工程学报, 2010, 32(10): 1588-1593. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201010020.htm ZHANG Qiang-yong, CHEN Guang-xu, LIN Bo, et al. Development and application of high-geostress true 3D loading geomechanics model test system[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(10): 1588-1593. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201010020.htm
[7]	SEOKWON J, JONGWOO K, YOUNGHO S, et al. Effect of a fault and weak plane on the stability of a tunnel in rock a scaled model test and numerical analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(3): 1-6.
[8]	李英杰, 张顶立, 宋义敏, 等. 软弱破碎深埋隧道围岩渐进性破坏试验研究[J]. 岩石力学与工程学报, 2012, 31(6): 1138-1147. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201206008.htm LI Ying-jie, ZHANG Ding-li, SONG Yi-min, et al. Experimental research of progressive damage of surrounding rock for soft fractured deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1138-1147. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201206008.htm
[9]	KIANI M, AKHLAGHI T, GHALANDARZADEH A. Experimental modeling of segmental shallow tunnels in alluvial affected by normal faults[J]. Tunnelling and Underground Space Technology, 2016, 51: 108-119.
[10]	李元海, 林志斌. 透明岩体相似物理模拟试验新方法研究[J]. 岩土工程学报, 2015, 37(11): 2030-2039. LI Yuan-hai, LIN Zhi-bin. Innovative experimental method based on development of transparent rock mass materials for physical tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(11): 2030-2039. (in Chinese)
[11]	LI Y H, TANG X J, YANG S, et al. Evolution of the broken rock zone in the mixed ground tunnel based on the DSCM[J]. Tunnelling and Underground Space Technology, 2019, 84: 248-258.
[12]	李元海, 靖洪文, 曾庆友. 岩土工程数字照相量测软件系统开发与应用[J]. 岩石力学与工程学报, 2006, 25(增刊2): 3859-3866. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2006S2081.htm LI Yuan-hai, JING Hong-wen, ZENG Qing-you. Development and application of digital photogrammetry software package for geotechnical engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3859-3866. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2006S2081.htm
[13]	张乾兵, 朱维申, 孙林锋, 等. 数字照相量测在大型洞群模型试验中的应用研究[J]. 岩土工程学报, 2010, 32(3): 447-452. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201003026.htm ZHANG Qian-bing, ZHU Wei-shen, SUN Lin-feng, et al. Application of digital photogrammetric techniques in 3D model tests on large caverns[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(3): 447-452. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201003026.htm
[14]	黎崇金, 李夕兵, 李地元. 含孔洞大理石岩破坏特性的颗粒流分析[J]. 工程科学学报, 2017, 39(12): 1791-1801. LI Chong-jin, LI Xi-bing, LI Di-yuan. Particle flow analysis of fracture characteristics of marble with a single hole[J]. Journal of Engineering Science, 2017, 39(12): 1791-1801. (in Chinese)

施引文献(17)

期刊类型引用(11)

1.	袁金秀，朱正国，王道远，崔光耀，马济文，宋宝禄，田小路，章浩天. 跨导热断层隧道动力响应及震害机理分析. 铁道工程学报. 2025(01): 69-76 . 百度学术
2.	张艳. 基于衬砌混凝土等级对输水隧洞地震响应影响数值模拟. 黑龙江水利科技. 2024(02): 121-123+140 . 百度学术
3.	张文杰，魏懿，于啸波. 基于Midas的双线盾构隧道抗震性能研究. 黑龙江工业学院学报(综合版). 2024(12): 140-147 . 百度学术
4.	黄娟，龙浩风，周世杰，施成华. 地震作用下大断面隧道衬砌结构的动力损伤特性. 华南理工大学学报(自然科学版). 2023(04): 124-134 . 百度学术
5.	张卜，卢立东，钟紫蓝，姬若愚，杜修力. 竖井结构初衬及二次衬砌竖向地震响应解析解. 西安建筑科技大学学报(自然科学版). 2023(02): 196-204 . 百度学术
6.	金波，田俊彤，方棋洪. 浅埋海底隧道围岩应力复势函数显式解. 力学学报. 2023(07): 1505-1516 . 百度学术
7.	丁文其，丁浩，门燕青，马非，马少坤，王士民，王万平，王帅帅，王圣涛，王亚琼，王传武，王树英，王剑宏，王智佼，毛锦波，方勇，邓涛，叶飞，申志军，田方正，付艳斌，冯冀蒙，吕勇刚，任锐，刘大刚，刘帅，刘永胜，刘学增，闫治国，孙文昊，孙纬宇，阳军生，李亚隆，李科，李然，李鹏飞，杨华，何伟，闵凡路，汪成兵，汪波，宋天田，张冬梅，张成平，张杨，张国柱，张俊儒，张亮亮，张高乐，张稳军，陈文尹，陈建忠，陈枰良，陈健，林志，罗彦斌，竺维彬，金大龙，周熙俊，郑余朝，官林星，房倩，封坤，赵清碧，胡斌，柳献，禹海涛，钟祖良，贺维国，耿萍，晏启祥，徐平，凌同华，高攀，郭卫社，黄阜，黄俊，黄清飞，曹校勇，龚彦峰，龚琛杰，梁庆国，董飞，韩兴博，傅金阳，曾艳华，管晓明，潘勇. 中国交通隧道工程学术研究综述·2022. 中国公路学报. 2022(04): 1-40 . 百度学术
8.	周耀强，石文广，唐欣薇，杨轩. 考虑动水压力的输水隧洞-层状地基地震响应分析. 水利水电技术(中英文). 2022(08): 101-111 . 百度学术
9.	赵辰洋，罗毛毛，邱静怡，倪芃芃，赵锋烽. 盾构隧道施工引起地层变形预测方法综述. 隧道与地下工程灾害防治. 2022(03): 31-46 . 百度学术
10.	肖鑫华. 基于数值模拟对深埋引水隧洞地震响应研究. 水利科技与经济. 2022(12): 105-109+115 . 百度学术
11.	禹海涛，陈功. 深部富水岩石拱形隧道地震响应解析解. 中南大学学报(自然科学版). 2021(08): 2783-2792 . 百度学术