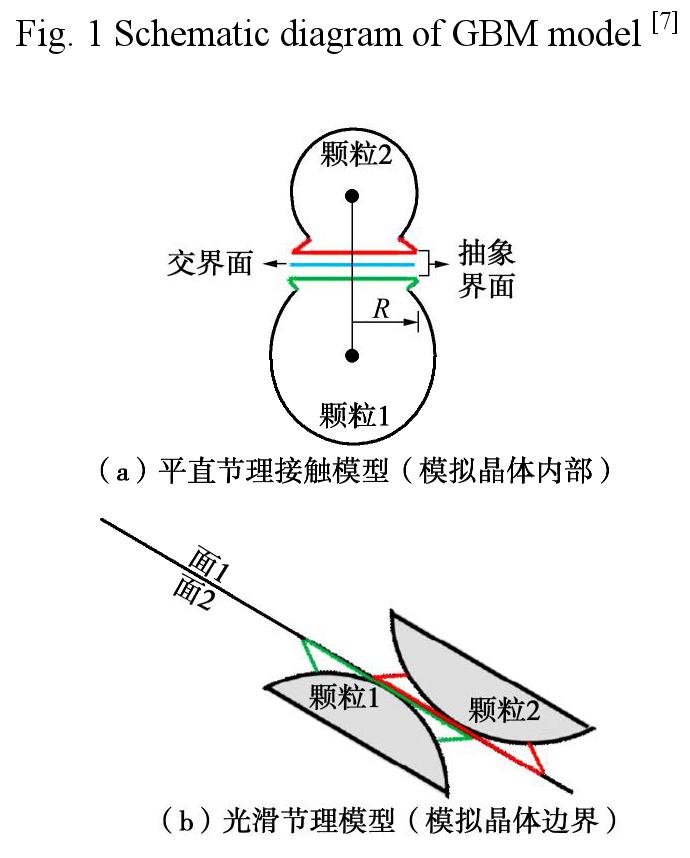
Influence of meso-structure heterogeneity on granite strength and deformation with particle flow code
-
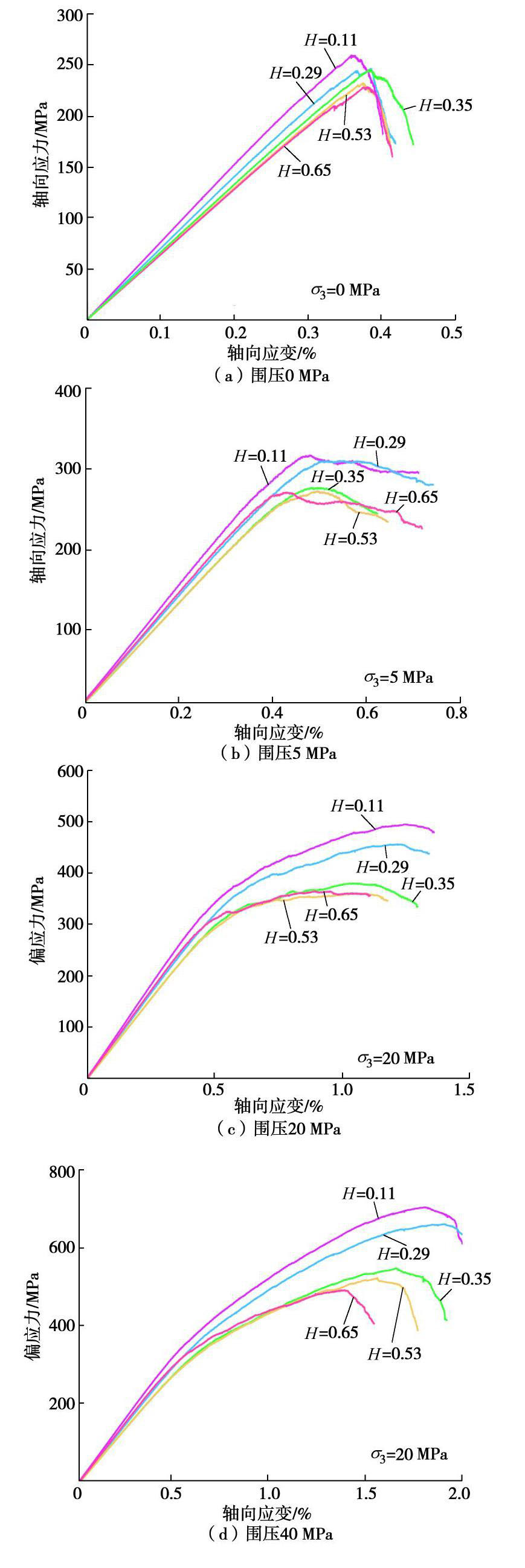
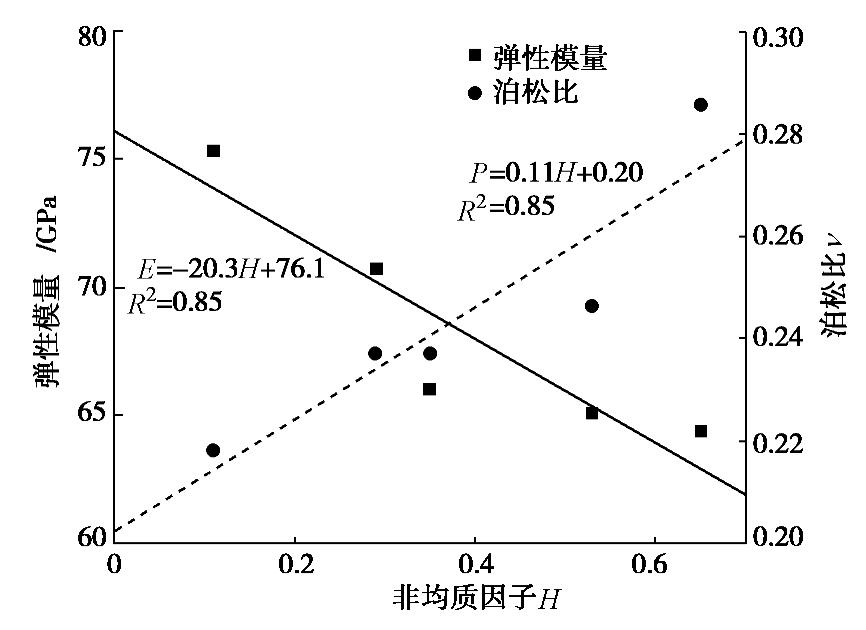
摘要: 基于等效晶质模型建模方法,利用颗粒流软件PFC2D实现对花岗岩细观结构的重建,开展了一系列不同围压下的花岗岩常规三轴压缩试验研究。揭示了晶体粒径分布所造成的细观结构上的非均质性和Mohr–Coulomb强度准则和Hoek–Brown强度准则中各参数的关系以及对岩石脆性的影响。研究结果表明,非均质性对岩样受压加载情况下的应力–应变曲线具有显著的影响。随着非均质因子增加,岩石由均质变为非均质,弹性模量逐渐减小,泊松比增加。随着非均质性因子的增加,岩石抗压强度减小、内聚力增加、内摩擦角减小。对同一类花岗岩而言,Mohr–Coulomb强度准则和Hoek–Brown强度准则中各参数的取值并非恒定,而是一定程度上依赖于内部的细观结构。当岩石细观结构变化时,两种强度准则中的参数也随之改变。细观结构的非均质性对岩石的脆性指标影响较大,随着非均质性因子的增加,岩石脆性指标减小。Abstract: By reconstructing the meso-structure of granite using the particle flow software PFC2D based on the grain-based model, a series of conventional triaxial compression tests on granite under different confining pressures are carried out. The relationship between the heterogeneity of the meso-structure caused by crystal size distribution and the parameters of Mohr-Coulomb strength criterion and Hoek-Brown strength criterion as well as the brittleness of rock is revealed. The heterogeneity has a significant effect on the stress-strain curve of rock specimens under pressure loading. As the heterogeneity factor increases, the rock changes from homogeneous to heterogeneous, the elastic modulus decreases, and the Poisson's ratio increases. As the heterogeneity factor increases, the compressive strength of the rock decreases, the cohesive force increases, and the internal friction angle decreases. For the same type of granite, the values of the Mohr-Coulomb strength criterion and the Hoek-Brown strength criterion are not constant, but depend to some extent on the internal meso-structure. When the meso-structure of the rock changes, the parameters in the two strength criteria also change. The heterogeneity of the meso-structure has a great influence on the brittleness index of rock. With the increase of heterogeneity factor, the brittleness index decreases.
-
Keywords:
- heterogeneity /
- strength /
- deformation /
- granite /
- particle flow code /
- grain-based model
-
0. 引言
近年来,由于地下水、盐的迁移和全球气温升高等物理现象改变了土体的蠕变机理。使土体在地基处理、水利工程和道路桥梁工程中会出现不稳定的非均匀沉降,从而对工程建设和使用防护产生了一系列的影响[1-3]。
目前,对不含盐土体蠕变模型的研究已经较为成熟。现有的理论模型主要以经验模型、元件模型和弹黏塑性模型为主,并且三者都能够很好地描述在指定条件下土体的蠕变行为[4-6]。其中,Yin等[7-9]在等时间线和弹-黏塑性理论为基础建立了一维蠕变模型,该模型的本构理论简单,参数少并容易获得。此外还将其推广到一维应力松弛及三维应力状态下的蠕变和应力松弛。但是该模型不能描述盐渍土中土颗粒与孔隙溶液间离子相互作用关系及对蠕变效应的影响。
盐渍土是土中含有可溶性盐类,且盐分浓度较高的一类特殊土。而有关盐渍土固结蠕变的试验研究主要集中在氯盐渍土中。从采用完全侧限条件下的固结蠕变试验到三轴条件下的等压蠕变、剪切蠕变和应变率试验,并在此基础上采用盐溶液饱和后的冻结砂、黏土等岩土材料展开了一系列的研究讨论[10-14]。在与盐渍土相关的本构理论研究中,学者们提出了能够描述饱和状态下孔隙溶液与土颗粒相互作用的概念模型和分形模型。并以渗透吸力为媒介桥梁,作为描述盐渍土中化学力学耦合的重要指标。Barbour等[15]认为在盐溶液饱和后的土体中,由于土体的渗透性导致有效应力的增加,并且提出将有效应力和渗透吸力作为应力状态变量来描述土体的力学性质。Shivananda[16]、Rao等[17]分别讨论了外来盐对孔隙溶液渗透吸力的影响和Van't Hoff方程在有无Van't Hoff因子时计算值与试验值的误差范围。并且明确了在恒定荷载作用下,采用氯化钠和蒸馏水饱和后试样的应变差可以通过渗透吸力的增加来预测试样的渗透诱导固结。Xu等[18]在上述理论的基础上采用分形理论描述了Van't Hoff方程中的渗透系数,提出了一种新的有效应力计算方法。
通过渗透吸力来描述岩土材料中化学-力学耦合性质已经成为研究盐渍土本构的一种有效研究方法。但是现有的理论主要是通过浓液的溶度来反映土水体系的化学性质,无法实现孔隙溶液中化学离子的定量描述,并且相关研究也主要集中在饱和氯盐中。因此本文对分别采用蒸馏水、氯化钠溶液和硫酸钠溶液饱和后的试样进行了固结蠕变试验,讨论了硫酸盐渍土与氯盐渍土的固结蠕变特性。在Van't Hoff方程中引入Pitzer离子相互作用模型,实现了土颗粒与孔隙溶液间的离子相互作用描述。在Yin-Graham一维蠕变模型的框架下建立了饱和盐渍土的一维蠕变模型,并结合蠕变试验结果,对原有模型和改进模型进行了详细的对比分析。
1. 试验条件与结果
1.1 试样制作
试验用土取自兰州七里河区。邴慧等[19]研究表明,洗盐对土颗粒粒组和土体结构影响较为明显。因此表1给出了洗盐后土样的物理性质指标。
表 1 洗盐后土样的物理性质指标Table 1. Physical properties of soil samples after salt washing初始孔隙比e0 颗粒相对密度 液限 wL /%塑限 wP /%塑限指数 IP 土粒粒组含量/% d ≤0.005 mm 0.005 mm<d<0.075 mm d ≥0.075 mm 0.66 2.7 28.2 18.4 9.8 20.33 71.11 8.56 试验在杠杆式中压固结仪上进行,数据采集通过电子位移计和数据采集仪共同工作,不仅保证了采集数据的精度,也保证了数据采集的连续性。土样制做的主要步骤为:洗盐(蒸馏水)—风干—碾碎过筛(0.5 mm)—配水制样(无盐试样)—风干,主要步骤严格按照《土工试验方法标准》的要求。试样尺寸的大小为:直径6.18 cm,高度2 cm;制样含水率为16.88%,干密度为1.641 g/cm3。
试样饱和时先将干燥土样安放完成,然后向固结仪水槽中注一定浓度的盐溶液后立即加载。饱和溶液根据是否含盐与易溶盐种类分为蒸馏水、硫酸钠溶液和氯化钠溶液;其中硫酸钠和氯化钠溶液的浓度分设了3组,其质量摩尔浓度分别为0.6,1.2,1.8 mol/kg。其次硫酸盐渍土对应上述质量摩尔浓度的质量分数分别为7.6%,14.6%,20.4%,氯盐渍土对应上述质量摩尔浓度的质量分数分别为3.4%,6.6%,9.5%。在试验过程中为了保持溶液浓度、试验温度(
25℃±1℃ )和饱和程度不变,在试验过程中设置了防止溶剂蒸发和保温隔热装置,并且在加载周期内保证水槽水位基本不变。1.2 试验结果
(1)固结试验
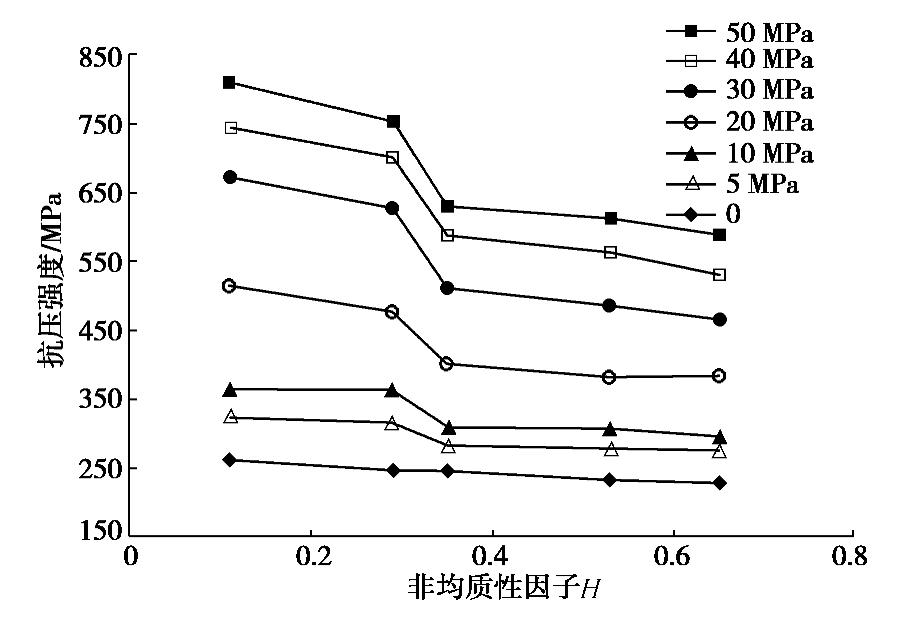
固结回弹试验结合土样的物理特性将加荷卸荷顺序设计为50,100,200,300,400,800,1600,800,400,300,200 kPa,每级荷载持续时间为24 h。图1给出了采用不同溶液饱和下的固结试验结果。从图1中发现非盐渍土与盐渍土的固结曲线存在明显的差异,而且采用硫酸钠和氯化钠溶液饱和后的盐渍土固结曲线也有所不同。通过观察图1发现,易溶盐对压缩变形的影响是贯穿于整个固结回弹过程中的。从而导致了在不同固结应力下,相同浓度的同类盐渍土对压缩变形的贡献是基本相等的。这与图1所表现出在50~1600 kPa的固结曲线和1600~200 kPa的回弹曲线几乎平行的结果相符合。这也证实了孔隙溶液的变化不会改变土体的压缩系数、压缩指数与回弹再压缩指数[13-14]。
(2)蠕变试验
蠕变是土体的超静孔隙水压力消散后,有效应力不变的情况下土体继续被压缩的宏观表象。也可以认为是在排水固结过程中发生的次固结压缩。图2描述了土样分别在蒸馏水、硫酸钠和氯化钠溶液饱和下的恒载蠕变情况。其中图2(a)~(c)分别是在200,400,800 kPa作用下的蠕变过程,直观地反映了盐渍土与非盐渍土蠕变行为的差异。
对比同一荷载情况下3种孔隙溶液饱和后的蠕变情况,发现孔隙溶液中盐分的存在增大了土体的初始蠕变变形与最终蠕变量。而这种增大的程度与含盐种类和含盐量息息相关。其次,盐渍土与非盐渍土的蠕变稳定时间明显不同,但是不同种类盐渍土的蠕变稳定时间在试验中没有表现出较为明显的差异。当荷载为200 kPa时,蒸馏水饱和下的蠕变时间大约在4.8 d,而由盐溶液饱和后的蠕变时间为6 d左右。表明土体盐渍化后的蠕变性明显要强于非盐渍化。同时还发现在盐溶液浓度为1.8 mol/kg时,经硫酸钠和氯化钠溶液饱和后的试验结果恰好与0.6和1.2 mol/kg的结果相反,同时在400,800 kPa和固结试验中也表现出了类似的结果。造成这种现象的原因可能是当浓度超过1.2 mol/kg时,由于硫酸钠溶液的活度小于氯化钠溶液,从而导致氯盐渍土表现出稍强的固结蠕变特性。
对比同盐类和盐度的盐渍土在不同荷载下的蠕变结果发现:随着荷载的增大,蠕变变形越大,并且蠕变稳定所需要的时间越长。当浓度为1.2 mol/kg时荷载为200,800 kPa下的蠕变稳定时间分别为5.8,6.1 d。
2. 饱和盐渍土的一维蠕变模型
2.1 渗透吸力
土中的吸力由基质吸力和渗透吸力(溶质吸力)组成,而在饱和土中一般认为总吸力等于渗透吸力。渗透吸力是由于孔隙水中溶解盐的存在导致土体中孔隙水化学势的降低,其实质是通过土体内外的渗透压,使土体内部出现负的孔隙水压力,从而导致有效应力的增加(图3)。
π=νRTcϕ, (1) 式中,
R 为通用的摩尔气体常数,R=8.32 J/mol⋅k ,T 为绝对K氏温度(T=298.15K),c 为孔隙溶液的浓度(mol/L ),ϕ 为溶质渗透系数,可根据Pitzer[22-23]提出的电解质渗透系数公式计算。当孔隙溶液只有一种溶质(MX)时:ϕ=1+|zMzX|fϕ+2mvMvXvBMXϕ+2m2(vMvX)3/2vCMXϕ, (2) 式中,
zM,zX 分别为电解质阳离子M和阴离子X的电荷数;v 为盐溶解后的总离子数,vM 为阳离子的离子总数,vX 为阴离子的离子总数,即v=vM+vX ;m 为盐溶液的质量摩尔浓度;fϕ 为Debye-Hückel项;BMXϕ 和CMXϕ 是离子相互作用系数。表2给出温度在298.15K时,采用式(1)计算氯盐渍土和硫酸盐渍土在不同浓度时的渗透吸力大小。将其与Van't Hoff方程计算结果和Fredlund等[24]采用滤纸法测试结果进行了比较。说明该公式不仅明确了土粒与孔隙溶液间化学-力学耦合效应的离子作用,而且有效地改善了使用Van't Hoff方程计算时随浓度增大而产生的较大误差。
表 2 298.15K时不同浓度氯化钠和硫酸钠溶液的渗透吸力Table 2. Osmotic suctions of sodium chloride and sodium sulfate solutions with different concentrations at 298.15K(kPa) 浓度/(mol·L-1) NaCl Na2SO4 0.2 915.11 1119.33 0.5 2281.01 2597.24 0.6 2742.22 3067.43 1.2 5593.46 5787.71 1.6 7584.01 7559.54 1.7 8093.60 8000.32 1.8 8608.10 8440.47 2.0 9651.91 9310.95 2.2 蠕变方程
土体的固结蠕变由可恢复的瞬时变形和不可恢复的延时变形组成。其中瞬时变形是完全弹性的,延时变形是黏性变形和塑性变形的总和,并且黏性变形和塑性变形是同时发生的。因此,基于上述假设,Yin等[7-8]给出了非盐渍土的一维蠕变方程:
εz=εepz0+λV0ln(σ∗zσ∗z0)+ξV0ln(tt0)。 (3) 式中
σ∗z 为有效应力;εepz0 为黏性应变为零时的弹塑性应变,即σ∗z=σ∗z0 时对应的应变;V0 为土体的初始比体积,V0=1+e0 ;λ/V0 为参考时间线的斜率;ξ/V0 为蠕变曲线在εz−lnt 中直线段的斜率;t=t0+te ,t0 ,te 分别为参考时间和等效时间。饱和盐渍土在轴向荷载作用下的应力状态变量可以理解为由传统的有效应力和颗粒孔隙间的净排斥力组成,且两部分应力可以看成一个应力状态变量。其中可以通过渗透压将颗粒间的排斥应力变化与流体间的渗透吸力联系起来,满足了渗透吸力作为应力状态变量的一致性条件[15-18]。因此饱和盐渍土的总有效应力由传统有效应力和有效渗透应力组成,即
σ∗=σ∗z+σ∗π。 (4) 式中
σ∗z 为传统的有效应力,其值由Terzaghi提出的饱和土的有效应力原理计算,即σ∗z=σz−uw ;σ∗π 为有效渗透应力,σ∗π=χπ ,χ 是量纲为“1”的参数,且0<χ<1 。将式(4)代入式(3)可得到改进的饱和盐渍土一维蠕变模型:
εz=εep0+λV0ln(σ∗σ∗0)+ξV0lntt0。 (5) 3. 模型参数
本文是在Yin-Graham模型的框架上考虑了盐渍土中孔隙盐溶液的有效渗透应力对固结蠕变的贡献;因此模型参数包含了原有的Yin-Graham模型参数外(
σ∗0 ,εep0 ,λ/V0 ,ξ/V0 ,t0 ),还新增了描述渗透应力的参数(χ ,fϕ ,BMXϕ ,CMXϕ )。3.1 Yin-Graham模型参数
基本参数
σ∗0 ,εep0 和λ/V0 可以通过24 h固结试验测得,其中λ=Δe/[ln(σ∗/σ∗0)] ,由试验结果得到λ 的值不随孔隙溶液改变。图4分别给出了σ∗0 和λ 的取值方法,其中根据图1的试验结果和σ∗0 的取值方法发现σ∗0 受土中含盐种类和含盐量的影响显著,故不同溶液饱和下的σ∗0 也不尽相同,而εep0 为σ∗=σ∗0 时的应变。t0 为参考时间,取t0=10 min 。盐渍土的蠕变系数
ξ/V0 不是一个定值,它会随着荷载和含盐量的变化而改变。表3给出了400 kPa和800 kPa作用下的计算结果,结果显示蠕变系数与压缩指数、回弹指数不同,它会随着荷载和渗透吸力的增大而增大。表 3 模型参数Table 3. Model parameters孔隙溶液 浓度m/(mol·kg-1) σ∗0 /kPa蠕变系数 ξ/V CMXϕ /(kg2⋅mol−2 )fϕ /(kg⋅mol)12 BMXϕ /(kg⋅mol−1 )400 kPa 800 kPa 蒸馏水 0 79 0.03053 0.03284 0 0 0 氯化钠 0.6 77.12 0.03146 0.03634 0.00106 -0.1572 0.1307 1.2 71.05 0.03494 0.03730 -0.1853 0.1054 1.8 61.21 0.03626 0.03859 -0.2012 0.0944 硫酸钠 0.6 75.09 0.03306 0.03655 -0.00483 -0.2012 0.1098 1.2 69.26 0.03466 0.03710 -0.2267 0.0670 1.8 64.40 0.03552 0.03827 -0.2401 0.0550 3.2 有效渗透应力参数
有效渗透应力是渗透吸力的宏观表达,而渗透吸力又通过渗透系数和溶液浓度描述盐渍土的化学物理性质。因此参数包含了模型参数
χ 和离子相互作用参数(fϕ ,BMXϕ ,CMXϕ )。并且都是在恒定的体积、温度和化学状态下的拟合参数与试验参数。其中fϕ 和BMXϕ 采用下式计算[22]:fϕ=−AϕI1/21+θI1/2, I=(1/2)∑miz2i, (6) BMXϕ=DMX0+DMX1exp(α1I1/2)+DMX2exp(α2I1/2)。 (7) 式中
Aϕ 为Debye-Hückel参数,当温度等于25℃时,Aϕ=0.392 kg−1/2⋅mol−1/2 ;I 为离子强度;θ 为恒定常数,θ=1.2kg1/2/mol1/2 ;mi 为离子i 的质量摩尔浓度,mi=vim ;BMXϕ 的数值是由离子强度I 所决定的,当电解质为一价型时BMXϕ 值取前两项;此时α1=2 ;DMX0 ,DMX1 ,DMX2 是盐溶液中溶质阴阳离子决定的相互作用参数[25]。χ 是表征渗透吸力转化为有效渗透应力的效率参数。当χ=1 时,表示盐渍土的渗透吸力完全转化为有效渗透应力,即所有的溶液离子都与土颗粒发生反应。而χ=0 时,表明盐渍土中的易溶盐离子都没有与土粒相互反应。显然这两种极限状态是不存在的,因此认为χ∈(0,1) 。图5是在相同条件下参数χ 的不同取值情况,发现参数χ 的敏感性在计算蠕变变形时表现的不强,而本文通过模型计算与试验结果拟合分析,确定χ=0.15 。4. 模型验证
通过改进模型和Yin-Graham模型对饱和盐渍土和非盐渍土恒载蠕变结果进行对比分析。验证了改进模型对预测饱和盐渍土一维蠕变行为的有效性。
图6为400,800 kPa下饱和非盐渍土的蠕变试验结果与Yin-Graham蠕变方程式(3)计算结果的对比情况。根据图示结果发现,采用Yin-Graham一维蠕变模型能够很好地预测饱和非盐渍土的蠕变行为。
图7,8为分别采用硫酸钠溶液和氯化钠溶液饱和后的恒载蠕变试验结果及使用方程式(3),(5)计算结果的对比情况。从图中可以发现采用Yin-Graham蠕变方程式(3)无法准确预测饱和盐渍土的蠕变行为,总是小于试验结果。采用改进模型式(5)不仅能够在其数值上预测饱和盐渍土的蠕变效应,而且还能够在详细描述饱和盐渍土化学力学耦合效应的同时预测不同类饱和盐渍土的蠕变特性。
图7是饱和硫酸盐渍土的蠕变结果。对比分析了相同轴向荷载作用下和同浓度溶液饱和下的模拟结果。发现Yin-Graham模型在孔隙溶液较低时,其计算结果与试验结果很接近,而且随着轴向荷载的增加计算误差也有所减小。从总体上讲,计算误差的大小同盐渍土孔隙溶液浓度呈正比,而与轴向荷载成反比。图8是饱和氯盐渍土的模拟结果,表现出与硫酸钠盐渍土相同的规律。所以在低浓度高承载作用时,饱和盐渍土的蠕变应变量可以采用Yin-Graham模型预测。但是在较高浓度的饱和盐渍土中,Yin-Graham模型的适用性有所降低。此类现象正好同图1,2固结蠕变试验结果和表3渗透理论的结果相一致。
5. 结论
首先通过固结蠕变试验,分析了盐渍土与非盐渍土、硫酸盐渍土与氯盐渍土的固结蠕变特性。然后基于Pitzer离子相互作用模型和Van't Hoff方程,完善了饱和盐渍土中化学力学耦合效应的描述。并在Yin-Graham模型的基础上,建立了饱和盐渍土的蠕变模型。此外还将模型与试验结果进行了比较,得到以下3点结论。
(1)相同的土粒粒组、荷载和温度条件下,盐渍土较非盐渍土表现出更强的蠕变性;而硫酸盐渍土与氯盐渍土也表现出不同的固结蠕变效应,并且在高、低浓度时的固结蠕变行为表现出相反的结果。
(2)改进的Van't Hoff方程不仅能够更深层次地反映饱和盐渍土中易溶盐的离子化学性质,也降低了使用传统Van't Hoff方程的计算误差;为建立盐渍土本构模型提供了帮助。
(3)改进后的Yin-Graham一维蠕变模型,不仅能够描述饱和盐渍土中物理化学相互作用,而且可以更加有效地反应其蠕变行为。
-
表 1 GBM模型细观参数表
Table 1 Meso-scopic parameters of GBM model
种类 颗粒基本参数 晶体内部细观参数(平直节理接触模型) 晶体边界细观参数(光滑节理接触模型) 最小粒径/mm 半径比 密度/(g·cm-3) 刚度比 模量/GPa 模量/GPa 刚度比 抗拉强度/MPa 黏聚力/MPa 内摩擦角/(°) 法向刚度/(GPa·m-1) 切向刚度/(GPa·m-1) 抗拉强度/MPa 黏聚力/MPa 内摩擦角/(°) 石英 0.3 1.66 2.65 3.5 168 168 3.5 170 170 50 40000 10000 20 20 20 钾长石 0.3 1.66 2.56 1.5 140 140 1.5 145 145 35 斜长石 0.3 1.66 2.63 1.5 140 140 1.5 146 146 35 黑云母 0.3 1.66 3.05 1.0 100 100 1.0 85 85 30 表 2 室内试验[15]和本文模型宏观力学参数对比表
Table 2 Comparison of macroscopic mechanical parameters between experimental data[15] and numerical simulation results
试验类型 单轴抗压强度/MPa 弹性模量/GPa 泊松比 抗拉强度/MPa 室内 200±22 69±5.8 0.26±0.04 7.4±1.04 本文 245.8 66.0 0.24 10.2 表 3 强度准则拟合参数
Table 3 Fitting parameters of strength criterion
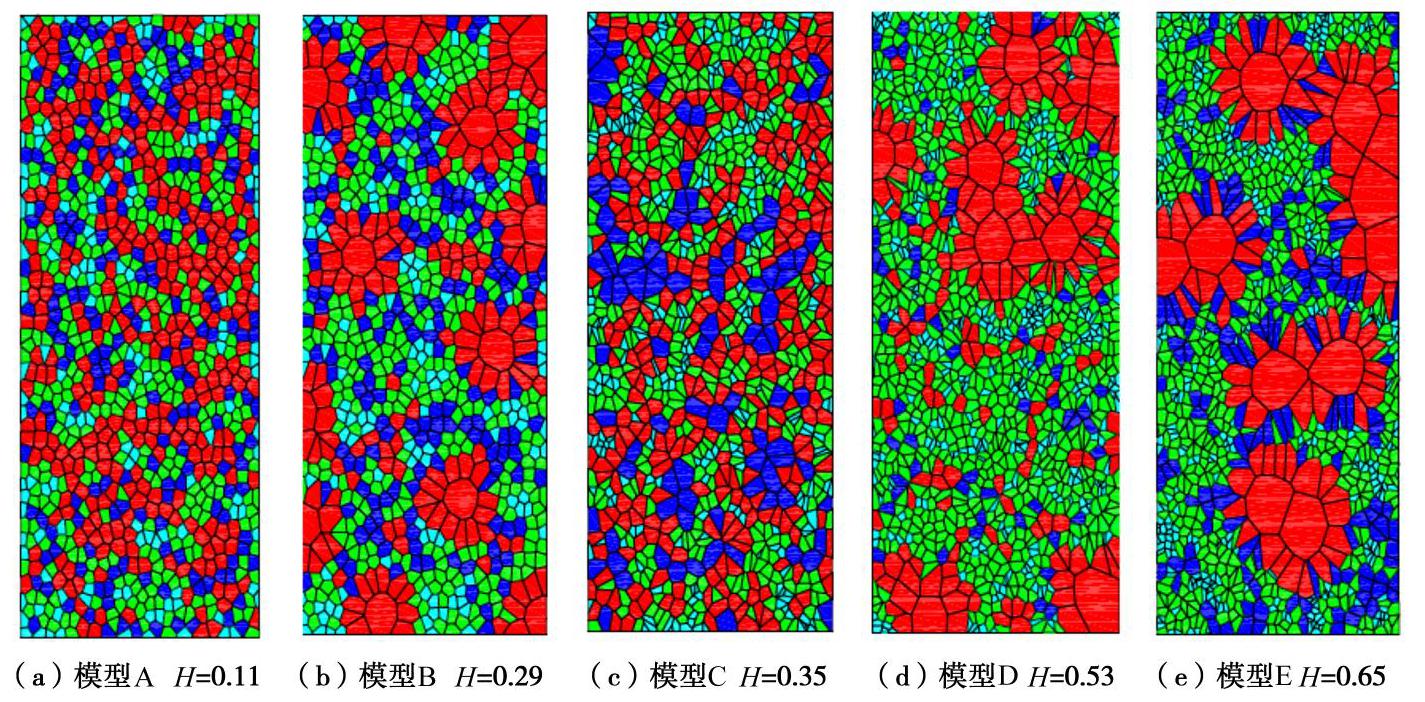
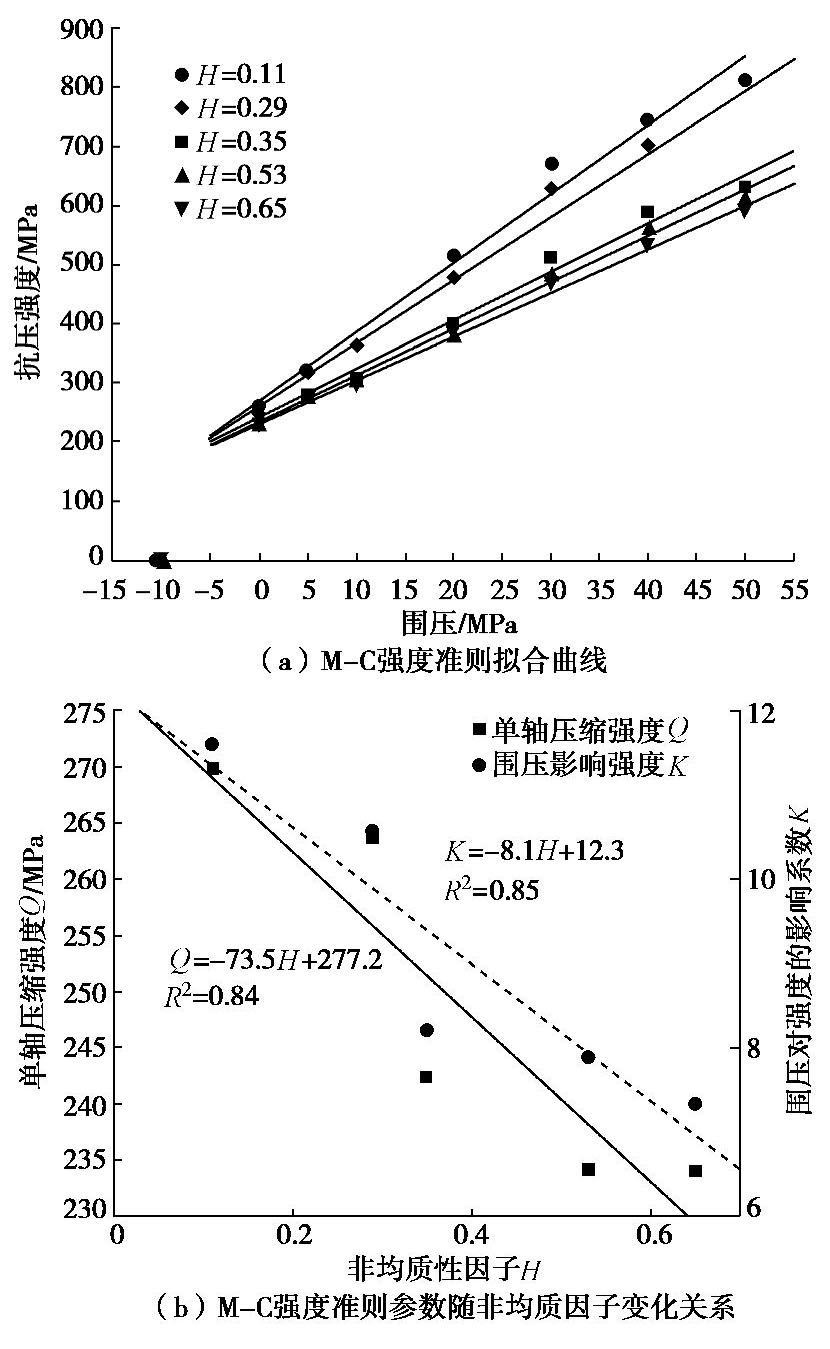
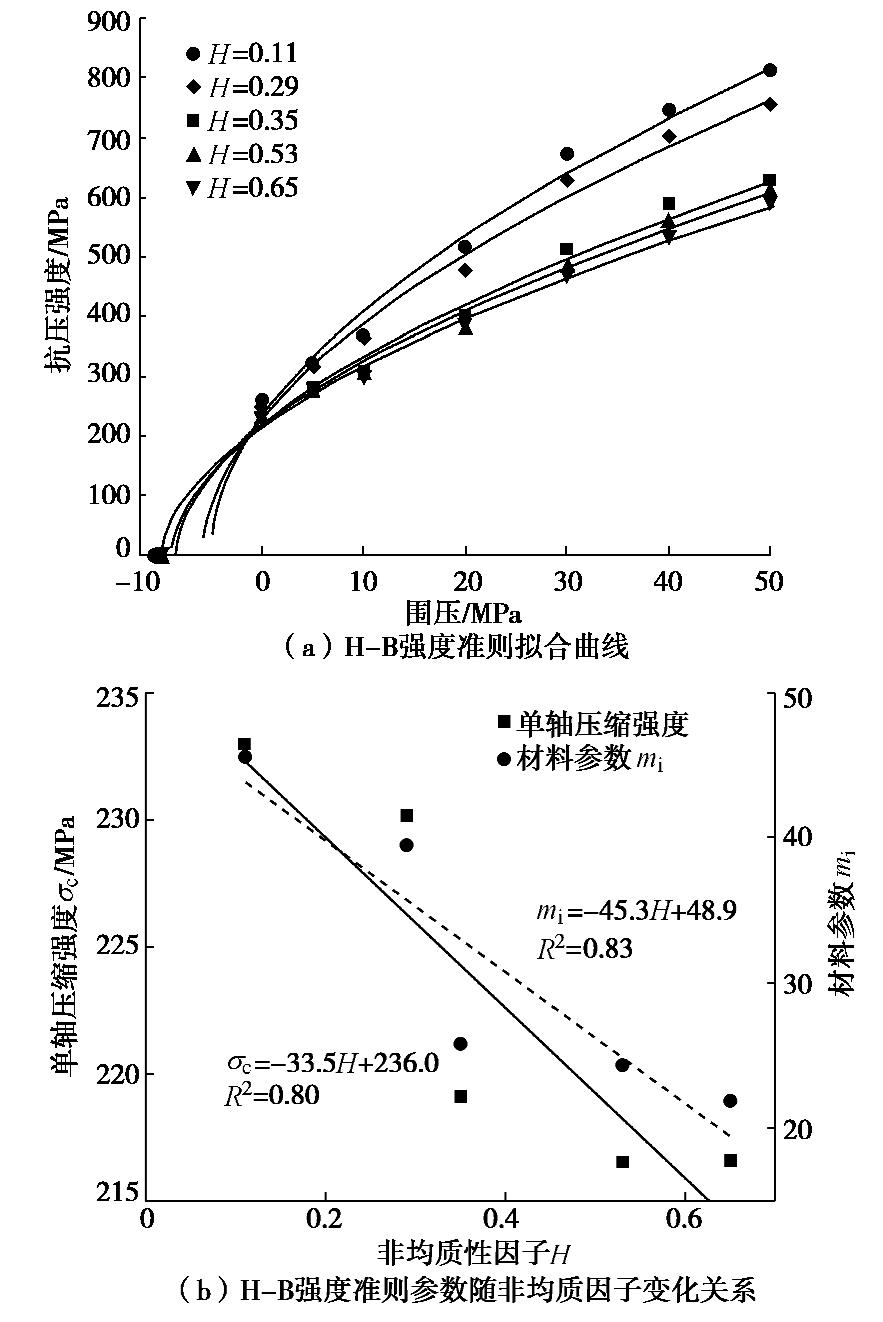
模型 非均质因子H M-C准则 H-B准则 Q/MPa K R2 σc /MPami R2 A 0.11 269.9 11.6 0.98 233.0 45.6 0.98 B 0.29 263.7 10.6 0.98 230.2 39.5 0.98 C 0.35 242.3 8.2 0.98 219.1 25.8 0.98 D 0.53 234.2 7.9 0.99 216.5 24.3 0.98 E 0.65 234.0 7.3 0.99 216.6 21.9 0.99 -
[1] WANG J. High-level radioactive waste disposal in China: update 2010[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 2(1): 5-15.
[2] 尤明庆. 围压对岩石试样强度的影响及离散性[J]. 岩石力学与工程学报, 2014, 33(5): 929-937. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201405008.htm YOU Ming-qing. Effect of confining pressure on strength scattering of rock specimen[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(5): 929-937. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201405008.htm
[3] TANG C A, LIU H, LEE P, et al. Numerical studies of the influence of microstructure on rock failure in uniaxial compression-Part I: Effect of heterogeneity[J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(4): 555-569.
[4] LAN H, MARTIN C D, HU B. Effect of heterogeneity of brittle rock on micromechanical extensile behavior during compression loading[J]. Journal of Geophysical Research Solid Earth, 2010, 115, B01202.
[5] POTYONDY D O. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364. doi: 10.1016/j.ijrmms.2004.09.011
[6] POTYONDY D O. A grain-based model for rock: approaching the true microstructure[C]//Proceedings of the Rock Mechanics in the Nordic Countries, 2010, Kongsberg: 225-234.
[7] 胡训健, 卞康, 刘建, 等. 细观结构的非均质性对花岗岩蠕变特性影响的离散元模拟研究[J]. 岩石力学与工程学报, 2019, 38(10): 2069-2083. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910013.htm HU Xun-jian, BIAN Kang, LIU Jian, et al. Discrete element simulation study on the influence of microstructure heterogeneity on the creep characteristics of granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(10): 2069-2083. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910013.htm
[8] PENG J, WONG L N Y, TEH C I. Influence of grain size heterogeneity on strength and microcracking behavior of crystalline rocks[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(2): 1054-1073. doi: 10.1002/2016JB013469
[9] LIU G, CAI M, HUANG M. Mechanical properties of brittle rock governed by micro-geometric heterogeneity[J]. Computers and Geotechnics, 104: 358-372. doi: 10.1016/j.compgeo.2017.11.013
[10] 水利水电工程岩石试验规程:SL264—2001[S]. 2001. Rock Test Regulations for Water Conservancy and Hydropower Engineering: SL264—2001[S]. 2001. (in Chinese)
[11] HOEK E, BROWN E T. Empirical strength criterion for rock masses[J]. ASCE Journal of Geotechnical Engineering Division, 1980, 106(GT9): 1013-1035.
[12] MARTIN C D, CHANDLER N A. The progressive fracture of Lac du Bonnet granite[J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts, 1994, 31(6): 643-659.
[13] ZHANG Q, ZHU H H, ZHANG L Y, et al. Effect of micro-parameters on the Hoek-Brown strength parameter mi for intact rock using particle flow modeling[C]//The 46th US Rock Mechanics Geomechanics Symposium, 2012, Chicago: 2187-2193.
[14] 周辉, 孟凡震, 刘海涛, 等. 花岗岩脆性破坏特征与机制试验研究[J]. 岩石力学与工程学报, 2014, 33(9): 1822-1827. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201409013.htm ZHOU Hui, MENG Fan-zhen, LIU Hai-tao, et al. Experimental study on characteristics and mechanism of brittle failure of granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1822-1827. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201409013.htm
[15] MARTIN C D. The Strength of Massive Lac du Bonnet Granite Around Underground Opening[D]. Winnipeg: University of Manitoba, 1993.
[16] ZHOU J, LAN H X, ZHANG L Q, et al. Novel grain-based model for simulation of brittle failure of Alxa porphyritic granite[J]. Engineering Geology, 2019, 251: 100-114. doi: 10.1016/j.enggeo.2019.02.005
[17] Itasca Consulting Group Inc. PFC, Version 5.0[M]. Minneapolis: Itasca Consulting Group Inc., 2014: 1-2.
[18] JI P Q, ZHANG X P, ZHANG Q. A new method to model the non-linear crack closure behavior of rocks under uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 112: 171-183. doi: 10.1016/j.ijrmms.2018.10.015
[19] 陈国庆, 赵聪, 魏涛, 等. 基于全应力–应变曲线及起裂应力的岩石脆性特征评价方法[J]. 岩石力学与工程学报, 2018, 37(1): 51-59. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801005.htm CHEN Guo-qing, ZHAO Cong, WEI Tao, et al. Evaluation method of rock brittle characteristics based on full stress-strain curve and crack initiation stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 51-59. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801005.htm
[20] 李斌. 高围压条件下岩石破坏特征及强度准则研究[D]. 武汉: 武汉科技大学, 2015. LI Bin. Study on Rock Failure Characteristics and Rock Strength Criteria under High Confining Pressure[D]. Wuhan: Wuhan University of Science and Technology, 2015. (in Chinese)
[21] LUAN X, DI B, WEI J, et al. Laboratory measurements of brittleness anisotropy in synthetic shale with different cementation[C]//Proceedings of the 2014 SEG Annual Meeting. Denver, Society of Exploration Geophysicists, 2014: 3005-3009.
[22] HUCKA V, DAS B. Brittleness determination of rocks by different methods[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1974, 11(10): 389-392. doi: 10.1016/0148-9062(74)91109-7
[23] 韩振华, 张路青, 周剑, 等. 矿物粒径对花岗岩单轴压缩特性影响的试验与模拟研究[J]. 工程地质学报, 2019, 27(3): 497-504. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201903005.htm HAN Zhen-hua, ZHANG Lu-qing, ZHOU Jian, et al. Uniaxial compression test and numerical studies of grain size effect on mechanical properties of granite[J]. Journal of Engineering Geology, 2019, 27(3): 497-504. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201903005.htm
-
期刊类型引用(2)
1. 范雷,余美万,邬爱清,向前. 层间错动带水力耦合抗剪强度特性演化规律研究. 岩土力学. 2023(07): 1959-1970 .  百度学术
百度学术
2. 武倩宇,韩登林,张吉振,王晨晨,任晓海,林珍珍,苏苗苗,朱亚玲,张娟. 页岩储层中颗粒尺寸效应对微裂缝发育的影响:以威远地区志留系龙马溪组页岩储层为例. 中南大学学报(自然科学版). 2022(09): 3603-3614 .  百度学术
百度学术
其他类型引用(1)



 下载:
下载: