薄层充填岩石节理剪胀特性试验研究

肖维民; 余欢; 朱占元; 李锐; 刘伟超

doi:10.11779/CJGE202008015

薄层充填岩石节理剪胀特性试验研究 English Version

肖维民^{1, 2,},
余欢^{1, 2},
朱占元^{1, 2, ,},
李锐^{1, 2},
刘伟超^{1, 2}

1.
四川农业大学土木工程学院,四川　都江堰　611830
2.
四川农业大学村镇建设防灾减灾四川省高等学校工程研究中心,四川　都江堰　611830

基金项目:

国家自然科学基金项目 41877195

国家自然科学基金项目 41502242

详细信息

作者简介:
肖维民(1983—),男,博士,副教授,主要从事节理岩体力学和水力学等方面的教学和科研工作。E-mail：sicauxwm@163.com

通讯作者:
朱占元, E-mail：zhuzyuan910@163.com

中图分类号: TU43
计量
- 文章访问数: 300
- HTML全文浏览量: 23
- PDF下载量: 125
出版历程
- 收稿日期: 2019-10-19
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-07-31

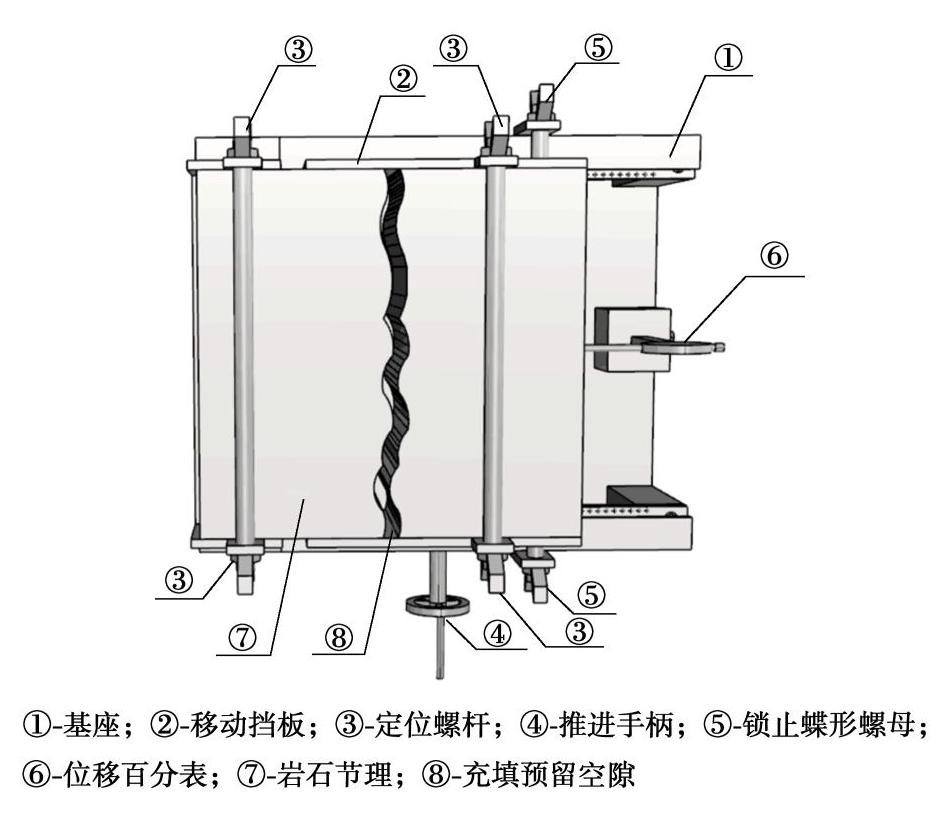
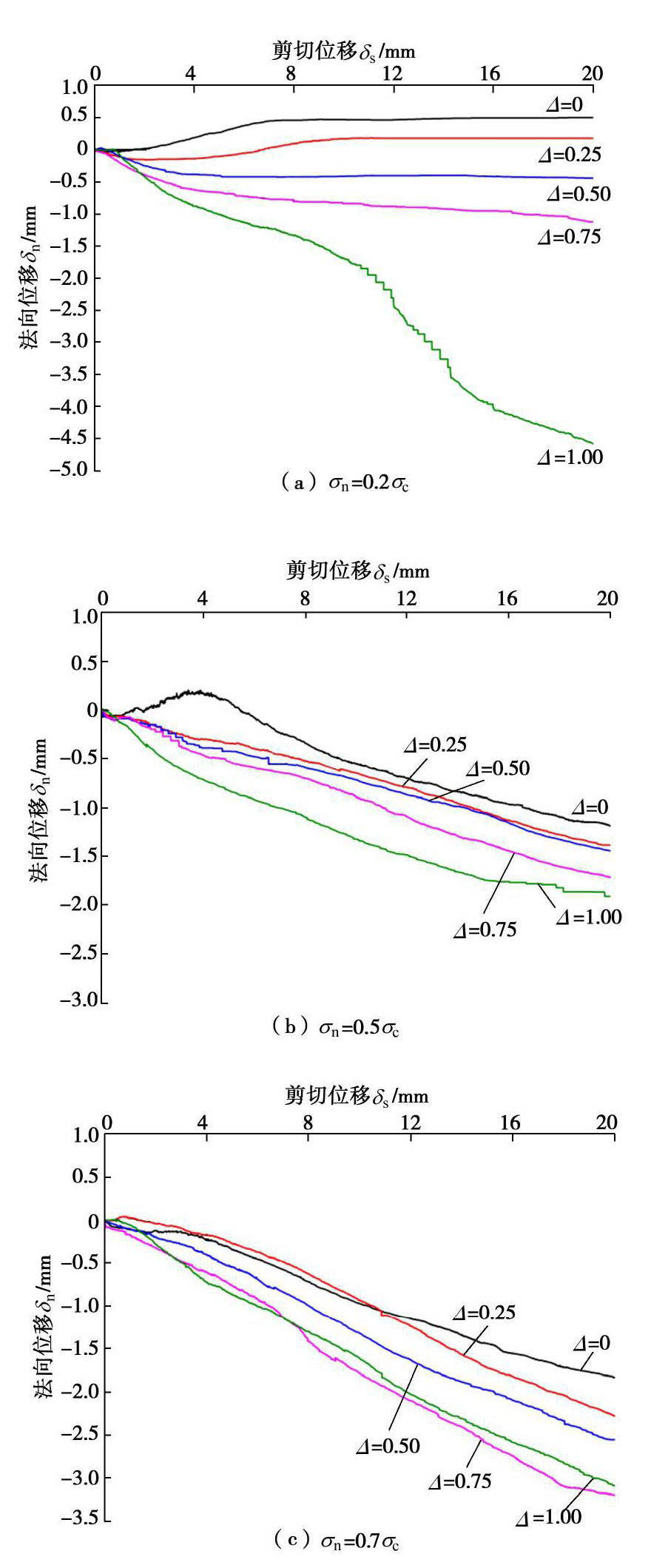
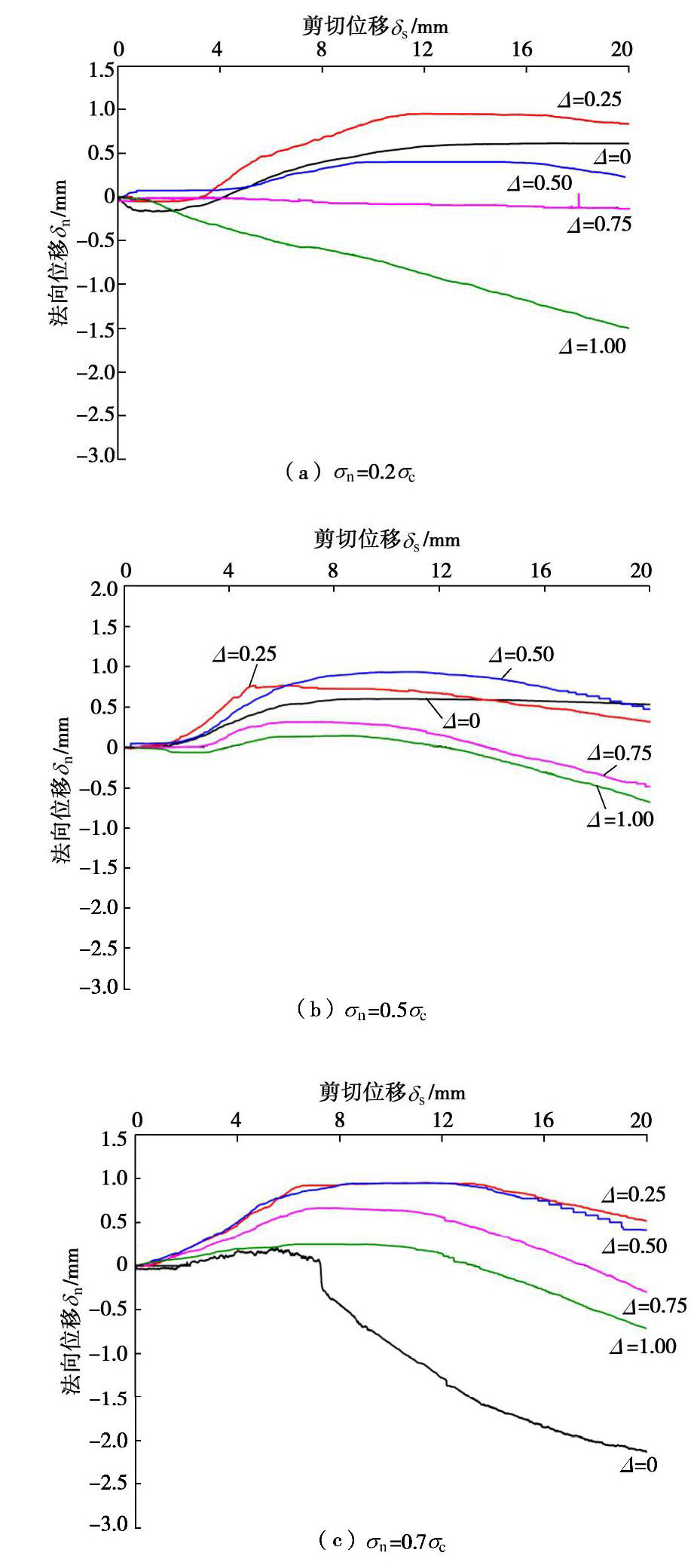
Experimental study on shear dilatancy characteristics of thinly-infilled rock joints

XIAO Wei-min^{1, 2,},
YU Huan^{1, 2},
ZHU Zhan-yuan^{1, 2, ,},
LI Rui^{1, 2},
LIU Wei-chao^{1, 2}

1.
School of Civil Engineering, Sichuan Agricultural University, Dujiangyan 611830, China
2.
Sichuan Higher Education Engineering Research Center for Disaster Prevention and Mitigation of Village Construction, Sichuan Agricultural University, Dujiangyan 611830, China

摘要

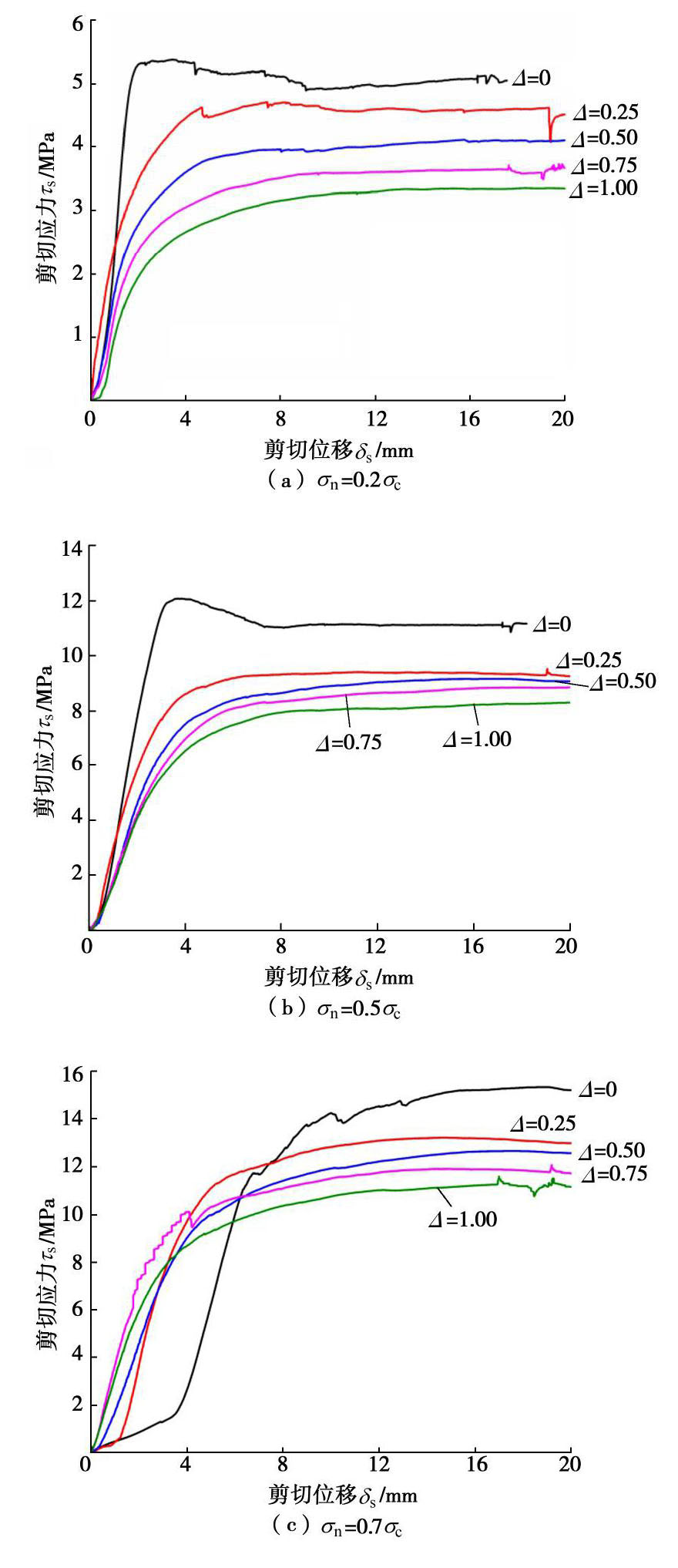
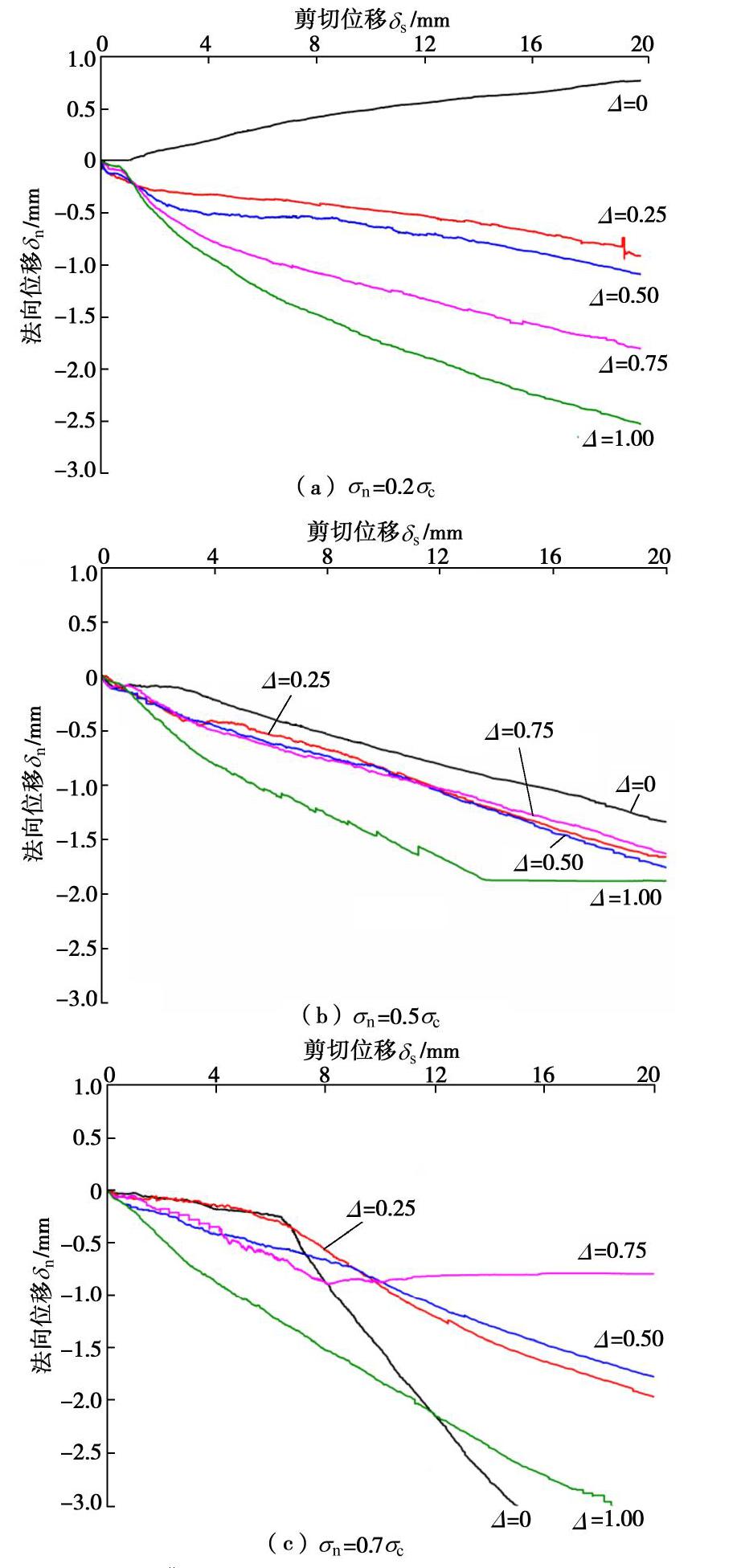
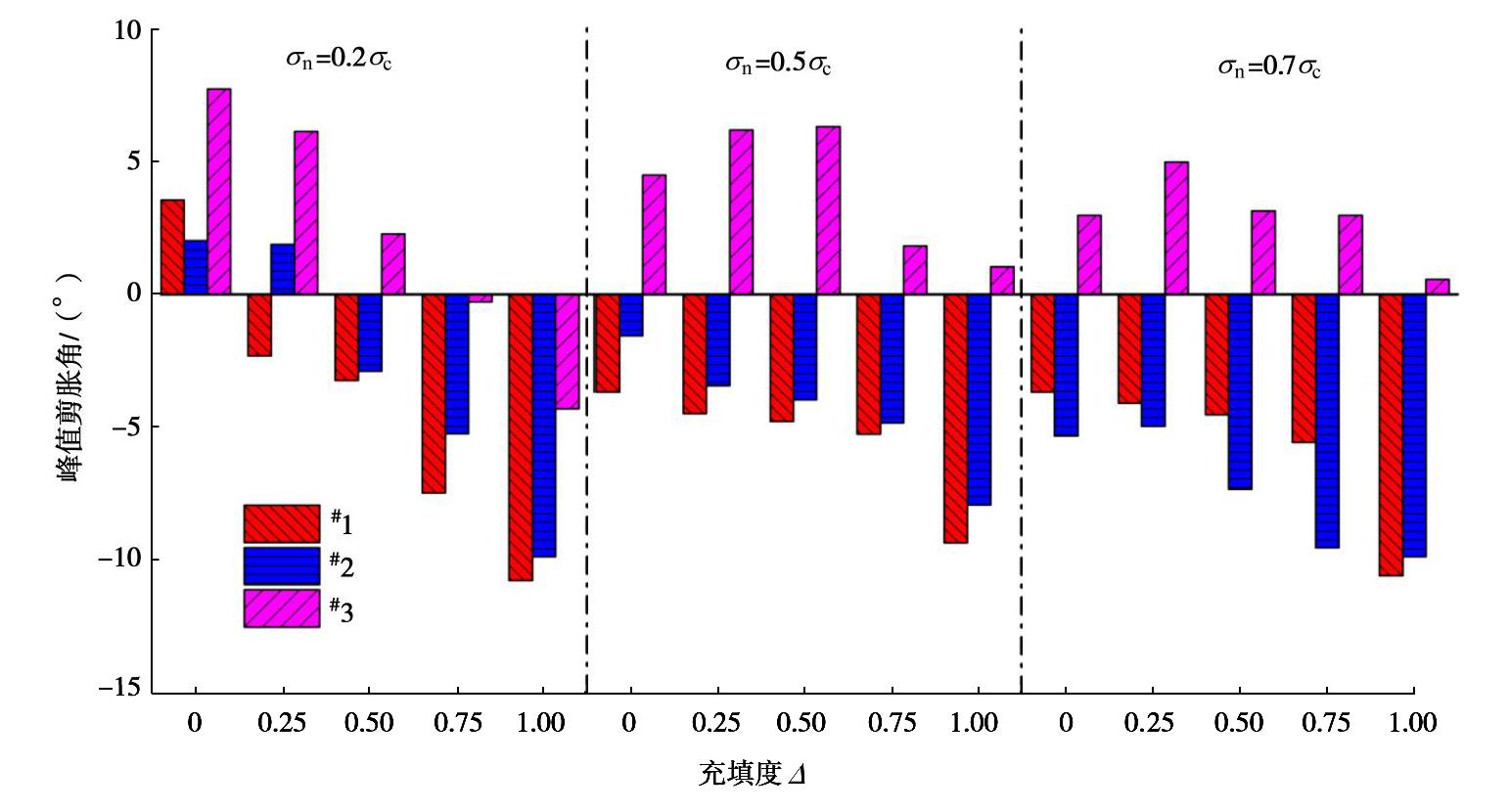
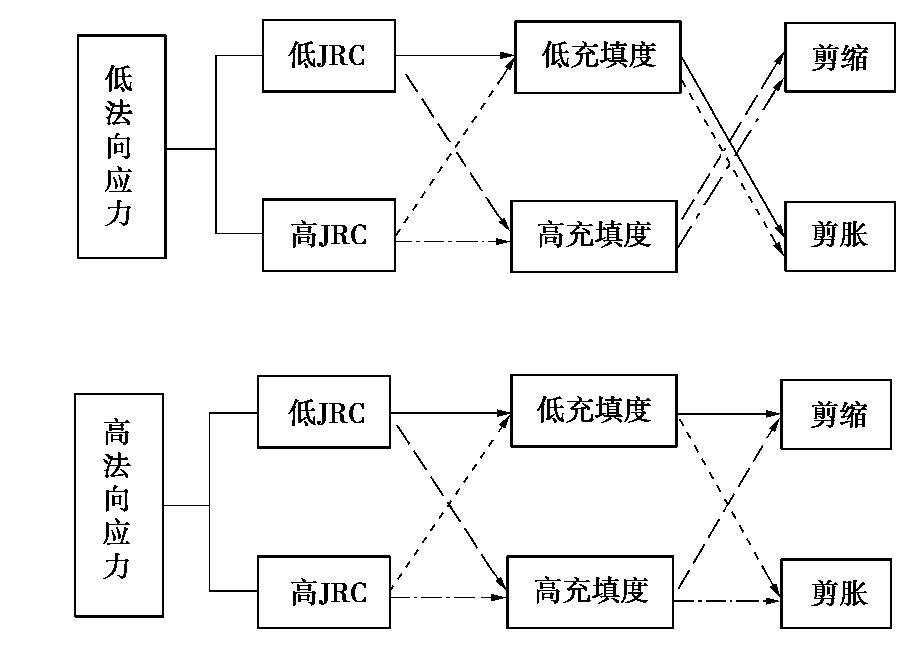
摘要: 岩石节理剪胀特性是影响节理渗流的重要因素,主要受节理表面粗糙性和法向应力的影响。而对于充填岩石节理而言,其剪胀特性还受到充填介质的影响。为了研究薄层充填岩石节理的剪胀特性,首先制备了3组具有Barton标准剖面线形貌特征、充填度 $Δ$ =0.00,0.25,0.50,0.75及1.00的薄层充填模拟岩石节理试件,然后在低、中、高三级法向应力下进行直剪试验,得到了薄层充填岩石节理试件法向位移–剪切位移曲线及其破坏特征。结果表明：在低法向应力条件下,节理表面粗糙性和充填度共同影响薄层充填岩石节理试件的剪胀特性,而在中高法向应力条件下,节理表面粗糙性是影响其剪胀特性的关键因素；薄层充填岩石节理破坏特征包含充填介质的剪切挤碎和节理上下表面粗糙凸起体被剪断两种,且随着充填度的增加,充填介质剪切挤碎逐渐占主导地位,成为薄层充填岩石节理试件的主要破坏特征。在此基础上,考虑充填介质对节理表面粗糙度系数JRC的弱化作用,建立了薄层充填岩石节理峰值剪胀角随充填度呈指数变化的经验关系式,并通过直剪试验数据和已有文献数据对其适用性进行了初步分析。
- 岩石力学 /
- 薄层充填岩石节理 /
- 直剪试验 /
- 剪胀 /
- 充填度
Abstract: The shear dilatancy has a significant effect on the seepage properties of rock joints, which is influenced by the roughness and normal stress acting on the rock joint surface. However, except for joint the surface roughness and normal stress, the infills also have an important effect on the shear dilatancy of infilled rock joints. So, in order to investigate the shear dilatancy of thinly-infilled rock joints, three groups of specimens which have the same surface roughness as Barton's standard profiles and different infill thicknesses are prepared firstly. Then the direct shear tests are performed on these specimens under three levels of normal stress, and the normal displacement vs. shear displacement curves and failure characteristics of thinly-infilled rock joints are obtained. The results show that the shear dilatancy is influenced by both the surface roughness and the infill thickness under low normal stress condition, whereas the surface roughness is the key factor influencing the shear dilatancy under middle and high levels of the normal stress. Furthermore, the failure modes of specimens include the shear and crush of infill particles and the shear of surface asperities, and the former failure mode becomes dominant with the increase of infill thickness. Then an empirical exponential expression is proposed to describe the peak shear dilatancy angle of thinly-infilled rock joints quantitatively by considering the weakening effect of infills on joint surface roughness, which is validated preliminarily by the direct shear test results and published data in literatures.
- rock mechanics /
- thinly-infilled rock joint /
- direct hear test /
- shear dilatancy /
- infill ratio

HTML全文

0. 引言

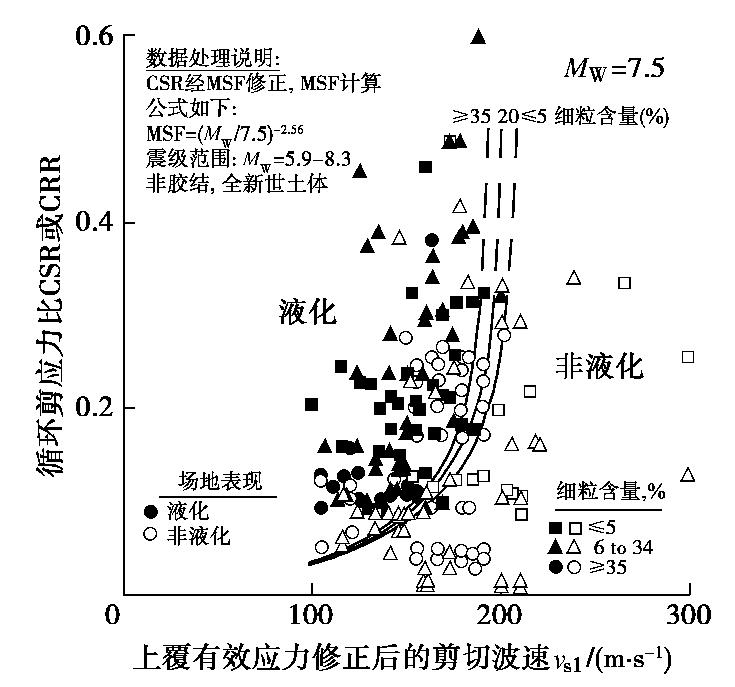
对于饱和砂土地震液化触发判别问题,应用最广泛的Seed简化判别方法主要建立在包含液化宏观震害现象、地震动加速度记录和场地原位测试指标三要素的地震液化实例数据和液化分界线的基础上^[1-3]。以基于原位剪切波速测试指标的液化实例为例,图1给出了地震液化和非液化实例,以及区分液化与否的分界线^[4]。由于强震液化事件彻底破坏易液化土体原有结构性,导致了消除液化土层既往沉积作用的“时钟重置”效应,使得震后获得的场地原位测试指标与真正控制场地抗液化性能的震前土体工程力学特性不对应。考虑到针对地震液化场地的原位测试一般发生在震后数天或数月甚至更长的时间里,图1中地震液化实例数据的剪切波速和相应的液化分界线可能存在与测试时间相关的系统误差。因此,研究震后易液化场地饱和砂土土层的剪切波速（或其它原位测试指标）随时间的变化规律,对正确认识现有基于原位测试指标的液化判别简化方法的可靠性并对震后测试指标进行合理修正具有重要的科学意义。

图 1 基于剪切波速的地震液化实例数据与分界线

Figure 1. v_s-based field case histories and liquefaction boundary curves

下载: 全尺寸图片幻灯片

土体在自然沉积过程中或者经受外荷载剧烈扰动后,其刚度和强度等工程力学参数在恒定应力状态下随时间变化的现象被称为“时间效应”,且该变化可以通过原位测试指标（例如,SPT、CPT和V_s）体现^[5-7]。例如,Andrus等^[8]通过静力触探与剪切波速的经验关系获得了原位砂土剪切波速和完全扰动后剪切波速的比值MEVR,初步揭示了地质时间尺度上的砂土时间效应（见图2）；周燕国等^[9]结合剪切波速（剪切模量）的Hardin公式^[10]和静力触探测试,提出了砂土时间效应的表征指标A_I,并利用不同地质年代砂土实测数据对其表征能力进行了检验。然而,上述研究主要面向地质沉积年代和土性测试指标的经验关系,关注数万年到数十万年甚至更长的地质时间尺度,并没有考虑地质沉积年代中可能受到的各种扰动（如强震事件）对土体工程力学特性的影响。以图2为例,深色椭圆圈内的数据并不符合图中拟合斜线的趋势,而这个时间范围（10^-1～10² a）正是实际工程服役寿命或者高烈度区强震重现周期的范围。Pavlenko等^[11]研究1995年神户地震中场地刚度演化问题,发现液化使得场地刚度急剧降低,但在震后较长一段时间内无法恢复到地震液化前的值。可见,对于实际工程,震后较短的时间尺度内场地土体的时间效应更具有工程意义,是影响易液化场地在余震中的地震响应和再液化可能性的重要因素。

图 2 土体测量与估算剪切波速比的时变趋势

Figure 2. Time variation of measured to estimated velocity ratio

下载: 全尺寸图片幻灯片

针对上述问题,本文对新西兰基督城的REHS强震台站在2010—2011年间的若干强震记录的尾波进行水平与竖向谱比（HVSR）分析,获得了该台站所在的易液化场地在地震前后小应变剪切刚度随时间的发展规律。在此基础上,提出了综合考虑主固结和次固结作用的震后饱和砂土小应变刚度计算模型,并合理预测了REHS台站场地震后刚度恢复变化过程。

1. 场地条件与强震台站记录分析

HVSR方法通过对强震台站的三向加速度记录进行分析得到场地卓越频率以及场地土层结构分布,相比于其它场地频率分析方法,HVSR方法相对简单,能够基本消除震源和传播路径的影响,得到的场地卓越频率更可靠^[12-13]。场地的卓越频率与场地平均剪切波速的关系可表示为^[14]

$v_{savg} = 4 H f$ 。

(1)

式中, $v_{savg}$ 为场地平均剪切波速,H为场地土层厚度,f为场地卓越频率。

根据弹性理论,土体小应变剪切模量表达为

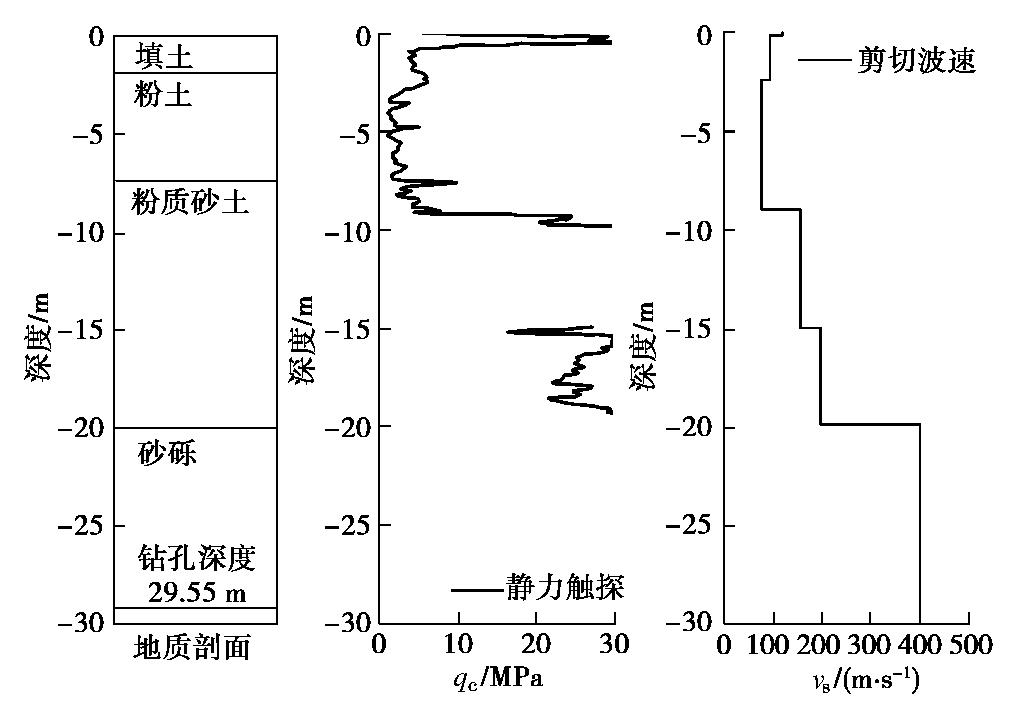
$G_{\max} = ρ \cdot v_{s}^{2}$ 。

(2)

本文针对新西兰基督城CBD区的REHS台站（见图3）,通过触发液化的强震本身和之后发生余震的加速度记录的尾波信号,获得场地卓越频率,根据式（1）,（2）分析从2010年以来3次强震事件之后场地刚度随时间变化规律。REHS台站所处场地的上覆软弱土层厚度约为20 m,存在较厚的饱和粉质砂土层和洁净砂土层,下卧刚度较大的砂卵石层（见图4）,是较典型的易液化场地^[15]。

图 3 基督城REHS强震台站位置（来源：www.nzgd.org.nz）

Figure 3. REHS strong motion station at Christchurch (source: www.nzgd.org.nz)

下载: 全尺寸图片幻灯片

图 4 REHS台站场地土层信息

Figure 4. Soil profile at REHS station site

下载: 全尺寸图片幻灯片

本文采用Geopsy软件进行HVSR分析,该软件能够多窗口同时计算H/V谱比和上覆土层的卓越频率f,并计算它们的平均值和方差。H/V谱比曲线的峰值对应的频率即为该尾波窗口时间对应的卓越频率。图5是尾波窗口选取和计算结果示意图,其中黑色实线代表所有窗口的平均值,两条虚线分别代表它的上、下限,竖向灰色条状区域代表了平均峰值所在的频率段。采用地震动记录的尾波进行HVSR分析获得场地卓越频率需满足一定的条件,即首先要保证主震后的选取的余震强度足够小,一是为了避免该余震事件对场地刚度恢复过程产生额外的显著影响,二是为了尾波段对应场地土体处于小应变弹性应变响应状态；其次,为保证数据处理结果的可靠性,均要求H/V谱比值大于2.0,而且卓越频率的误差在±0.3 Hz以内。

图 5 地震尾波HVSR谱比分析

Figure 5. HVSR analysis of seismic coda wave

下载: 全尺寸图片幻灯片

2. 震后场地小应变刚度演化规律

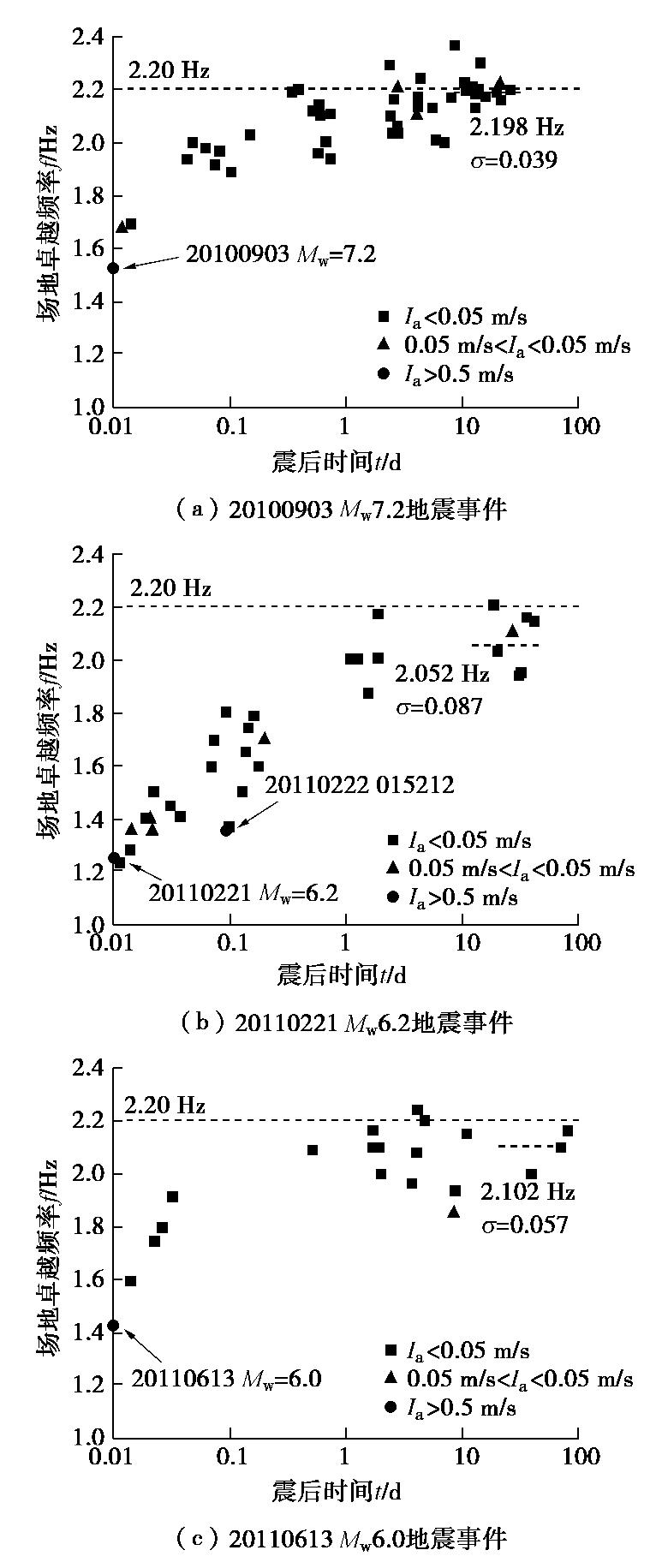
图6给出了REHS台站场地2010年至2011年间3次强震后场地卓越频率随时间的发展情况。考虑到每次强震事件之后大部分余震在台站的地震动强度都很小,可以忽略其对震后场地的进一步扰动作用。每张图上方的黑色虚线代表2010年9月3日M_w7.2地震事件之前场地的卓越频率（f_i=2.20 Hz）,由2010年大震之前的小震记录进行HVSR分析得到；右上角红色虚线表示强震事件后场地的稳定值,可视为下次强震前的场地卓越频率初始值。由图6可见,每次强震后场地刚度恢复至相对稳定的状态所需要的时间基本一致（为数天到数十天）,而且场地稳定后的卓越频率均值接近但低于最初的水平（即2.20 Hz）。

图 6 震后场地卓越频率时变规律

Figure 6. Evolution of fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

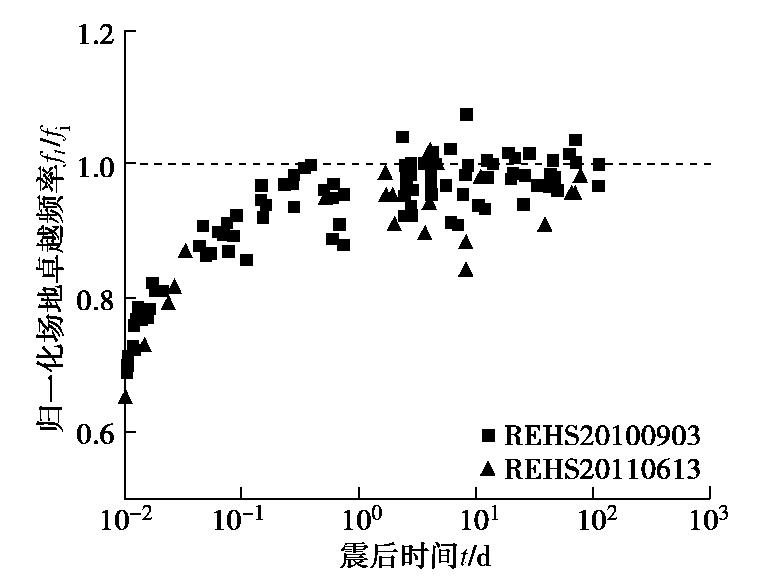
由图6（b）可见,20110221 M_w6.2地震事件中场地卓越频率受到强余震地震历史的影响,因此图7仅将图6（a）和（c）的归一化场地卓越频率（f/f_i）随时间发展规律归纳在一起。由图7可见,震后场地刚度恢复速率基本一致,呈现对数形式的增长,这与PENG等^[16-17]的研究发现类似。而基督城场地小应变刚度在震后10～100 d会有显著的恢复。根据Downes等^[18]的研究,2010年距上次基督城发生强震液化的时间间隔接近100 a,可以认为基督城典型易液化场地的新近沉积时间（或液化的重现周期）为100 a左右,所以尽管REHS台站场地的砂土层刚度在液化后的数月内会有较大的恢复,但仍小于震前水平。需要指出的是,在基督城的其它强震台站（如CBGS和CCCC台站）场地也观测到了类似规律^[19]。另外,注意到图7中同一时间对应的频率数据存在一定离散性,原因包括：首先,HVSR方法不能完全消除震源及传播路径的影响；其次,地震动加速度信号（尤其是小震事件）信噪比水平不同；再次,地下水位的季节性升降等环境变化带来的可能影响。

图 7 震后场地归一化卓越频率变化规律

Figure 7. Evolution of normalized fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

3. 饱和砂土震后小应变刚度计算模型

需要注意,Andrus等^[8]将砂土的MEVR参数用于剪切模量的时间效应修正,这种修正主要反映数十万年甚至更久的由于颗粒胶结引起的时间效应,不能合理反映砂土液化后短期内刚度的变化规律（即孔压消散与次固结引起的时间效应）,而大部分震后实例调查的原位测试均是在这一时间段获得的；其次,这种修正对特定地震和场地数据的依赖性较大,数据十分有限,规律的一般性不强。本节基于饱和砂土的主固结与次固结过程,提出了考虑有效应力变化和砂土颗粒间接触力均质化（包括孔隙比变化）这两个主要因素的震后饱和砂土小应变刚度计算模型。

3.1 主固结影响函数

首先考虑由孔压消散和孔隙变化引起的剪切模量增量,可采用Hardin公式表示土体小应变剪切模量与土体孔隙比及有效应力的关系：

$G_{\max} = A \cdot F (e) {({σ^{'}}_{m})}^{n}$ ,

(3)

式中,G_max为砂土小应变剪切模量,A为结构性参数,F(e)为孔隙比方程, ${σ^{'}}_{m}$ 为平均有效应力,n约等于0.5。

平均固结度U通常定义为

$U = \frac{S_{ct}}{S_{c \infty}}$ ,

(4)

式中,S_ct为地基某时刻的主固结变形,S_c∞为地基的最终主固结变形。

根据太沙基一维固结理论,平均固结度U为

$U = 1 - \sum_{m = 1}^{\infty} \frac{2}{M^{2}} e^{- M^{2} T_{v}}$ 。

(5)

式中,竖向固结时间因子T_v为

$T_{v} = \frac{k_{v} t}{H^{2} γ_{w} m_{v}}$ ,

(6)

式中,k_v为土的竖向渗透系数,t为固结时间,H为土层厚度, $γ_{w}$ 为水的重度,m_v为土体体积压缩模量。

设砂土震后初始孔隙比为e₀,主固结完成后孔隙比为e_c∞,固结中土体孔隙比为e_ct,则由式（4）可以得到土体平均固结度：

$U = \frac{e_{0} - e_{ct}}{e_{0} - e_{c \infty}}$ 。

(7)

超静孔压比与砂土有效应力的关系如下：

$1 - r_{u} (t) = {[\frac{{σ^{'}}_{m, t}}{{σ^{'}}_{m,i}}]}^{2}$ ,

(8)

式中, $r_{u} (t)$ 为t时刻砂土的超静孔压比, ${σ^{'}}_{m, t}$ 为t时刻砂土的有效应力, ${σ^{'}}_{m,i}$ 为砂土的初始最大有效应力。

考虑到在主固结阶段砂土剪切模量增长主要由有效应力增加和孔隙比减小引起的,而结构性变化的影响很小。因此本文假设砂土主固结过程中结构性参数A不变,结合式（3）,（7）,（8）得到砂土震后剪切模量随时间的变化函数如下：

$\frac{G_{pc} (t)}{G_{R}} = \frac{F (e_{0} - U e_{0} + U e_{c \infty})}{F (e_{c \infty})} {[1 - \frac{p_{0}}{σ^{'}} (1 - U)]}^{0.5}$ ,

(9)

式中,G_pc(t)为任意固结时刻的砂土小应变剪切模量,G_R为砂土在参考时间时的小应变剪切模量,一般参考时间t_R大于主固结时间t_p。

3.2 次固结影响函数

砂土次固结过程中,颗粒间接触力均质化（包括孔隙比减小）也是引起砂土刚度随时间增长的一个重要因素^[20-21]。本文采用Howie等^[22]基于室内试验提出的经验公式加以描述：

$\frac{G_{sc} (t)}{G_{R}} = 1 + \frac{Δ G}{G_{R}} \cdot \lg (\frac{t}{t_{R}})$ ,

(10)

式中,t为固结时间,t_R为参考时间,G_sc(t)为任意固结时刻的小应变剪切模量,G_sc,R为在参考时间的小应变剪切模量, $Δ G$ /G_sc,R为剪切模量增长速率,对于特定的土体需根据室内固结试验确定。

3.3 饱和砂土震后小应变刚度计算模型

在震后一定的时间段,砂土剪切模量变化受上述两个因素共同影响,本文假设这两种机理相互独立,结合式（9）,（10）得

$\frac{G (t)}{G_{R}} = 1 + \frac{Δ G_{pc} (t)}{G_{R}} + \frac{Δ G_{sc} (t)}{G_{R}}$ 。

(11)

式（11）结合 $G = ρ v_{s}^{2}$ 和 $v_{s} = 4 H f$ 可得到场地卓越频率随随时间发展的函数：

$\frac{f (t)}{f_{R}} = \sqrt{\frac{G (t)}{G_{R}}}$ 。

(12)

根据现有围绕基督城场地的研究成果,式（12）的参数取值如下：该场地上覆软弱土层厚20 m,主要由砂土和粉土组成,排水条件良好^[15]；根据CPT测试的I_c和渗透系数的经验关系^[23]取土层平均渗透系数k_v=2.5×10^-5 m/s；土层的平均压缩模量由动力触探锤击数与压缩模量的经验关系^[24]得到,取E_s=15.0 MPa；土层初始平均超静孔压比取p₀=0.8。另外,假设震后场地刚度需要经历震前同样的沉积时间才能恢复至2010年9月3日强震液化事件之前的震前值,则参考时间取为t_R=100 a。

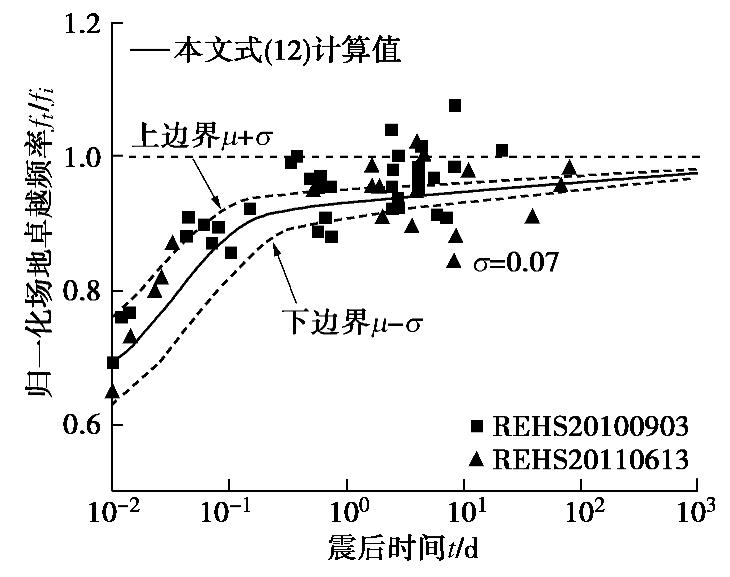
根据式（12）计算得到基督城REHS台站场地液化后基频随时间的发展规律如图8中的曲线所示,图中上、下两条边界线代表由于参数取值带来的标准差。由图8可见,该计算模型对图6（a）,（c）中的两次强震数据的预测效果较好,能够考虑震后一定时间内饱和砂土刚度的恢复规律。

图 8 震后刚度发展函数预测效果

Figure 8. Prediction of post-earthquake stiffness function

下载: 全尺寸图片幻灯片

4. 结论

为研究震后饱和砂土场地原位测试指标变化规律及其与震前值的差异,本文针对新西兰基督城的典型易液化场地,开展了从实际场地卓越频率监测分析到砂土小应变刚度计算模型的研究。主要结论如下：

（1）针对基督城系列强震,对REHS强震台站记录信号进行HVSR分析,揭示了震后场地刚度整体呈现指数形式的增长规律。场地小应变刚度会在震后经过数天的快速恢复后进入相对稳定的缓慢上升期。对于震前沉积时间较久的场地,场地刚度在震后短时间内难以恢复到震前水平,现有基于震后原位调查获得的液化实例数据应当根据震后原位测试时间进行适当的修正。

（2）假设震后场地刚度需要经历震前同样的沉积时间才能恢复至震前值,基于主固结与次固结过程提出了具有物理意义的饱和砂土震后小应变刚度计算模型,可估算基督城典型易液化场地在强震后平均小应变刚度随时间的发展规律。该计算模型为将特定场地的震后原位测试指标（如剪切波速）修正到对应的震前值提供了一种有效手段。

注意到本文所揭示的震后场地小应变刚度演化规律和所建议的计算模型及参数主要针对新西兰基督城场地,有必要进一步研究更多的其它地震和场地刚度演化规律,并获取各类易液化场地和土体参数,才能为将液化实例中的震后原位测试指标修正到震前原状土的对应值提供定量依据,提高当前基于液化实例调查的地震液化简化判别方法的准确性。

图 1 模拟岩石节理试件制备

Figure 1. Preparation of artificial rock joint specimens

下载: 全尺寸图片幻灯片

图 2 石英砂充填装置示意图

Figure 2. Schematic diagram of a device for filling quartz sands

下载: 全尺寸图片幻灯片

图 3 YZW50岩石剪切试验机

Figure 3. YZW50 rock shear system

下载: 全尺寸图片幻灯片

图 4 ^#1试件剪切应力–剪切位移曲线

Figure 4. Shear stress vs. shear displacement curves of specimen No.1

下载: 全尺寸图片幻灯片

图 5 ^#1试件法向位移–剪切位移曲线

Figure 5. Normal displacement vs. shear displacement curves of specimen No.1

下载: 全尺寸图片幻灯片

图 6 ^#2试件法向位移–剪切位移曲线

Figure 6. Normal displacement vs. shear displacement curves of specimen No.2

下载: 全尺寸图片幻灯片

图 7 ^#3试件法向位移–剪切位移曲线

Figure 7. Normal displacement vs. shear displacement curves of specimen No.3

下载: 全尺寸图片幻灯片

图 8 薄层充填岩石节理试件典型剪切破坏特征

Figure 8. Typical failure properties of thinly-infilled rock joints

下载: 全尺寸图片幻灯片

图 9 3组薄层充填岩石节理试件峰值剪胀角汇总结果

Figure 9. Summary of peak dilation angles of three groups of thinly-infilled rock joint specimens

下载: 全尺寸图片幻灯片

图 10 薄层充填岩石节理剪胀特性影响因素分析

Figure 10. Influencing factors of dilation property of thinly-infilled rock joints

下载: 全尺寸图片幻灯片

图 11 试验数据拟合分析曲线

Figure 11. Fitting curve of experimental data

下载: 全尺寸图片幻灯片

图 12 充填粉煤灰模拟岩石节理试件拟合曲线

Figure 12. Fitting curve of fly-ash-infilled artificial rock joints

下载: 全尺寸图片幻灯片

表 1 Barton标准节理剖面线^[2]

Table 1 Standard joint profiles proposed by Barton

编号	序号	JRC₀	平均起伏差h/mm
^#1	5	8~10	7.98
^#2	6	10~12	10.96
^#3	8	14~16	12.93

下载: 导出CSV

表 2 净水泥浆基本力学参数

Table 2 Basic mechanical parameters of cement slurry

参数	黏聚力c/MPa	内摩擦角φ/(°)	单轴抗压强度 $σ_{c}$ /MPa	弹性模量E/MPa
数值	10.35	27.89	28.3	3140

下载: 导出CSV

表 3 薄层充填岩石节理试件峰值抗剪强度试验结果

Table 3 Peak shear strengths of thinly-infilled rock joints

法向应力 $σ_{n}$	充填度	峰值抗剪强度τ_f / MPa
法向应力 $σ_{n}$	充填度	^#1	^#2	^#3
0.2 $σ_{c}$	0.00	5.378	6.290	7.654
	0.25	4.712	5.231	5.815
	0.50	4.121	4.277	4.933
	0.75	3.738	3.906	3.926
	1.00	3.209	3.298	3.414
0.5 $σ_{c}$	0.00	12.096	11.079	14.496
	0.25	9.541	10.008	11.091
	0.50	9.173	9.411	10.426
	0.75	8.869	8.902	9.176
	1.00	8.307	8.501	8.392
0.7 $σ_{c}$	0.00	15.353	15.402	15.493
	0.25	13.231	14.278	15.026
	0.50	12.672	13.499	13.738
	0.75	12.093	12.163	12.321
	1.00	11.610	12.222	11.277

下载: 导出CSV

表 4 薄层充填岩石节理试件峰值剪胀角试验值

Table 4 Results of peak dilation angle of thinly-infilled rock joint specimens

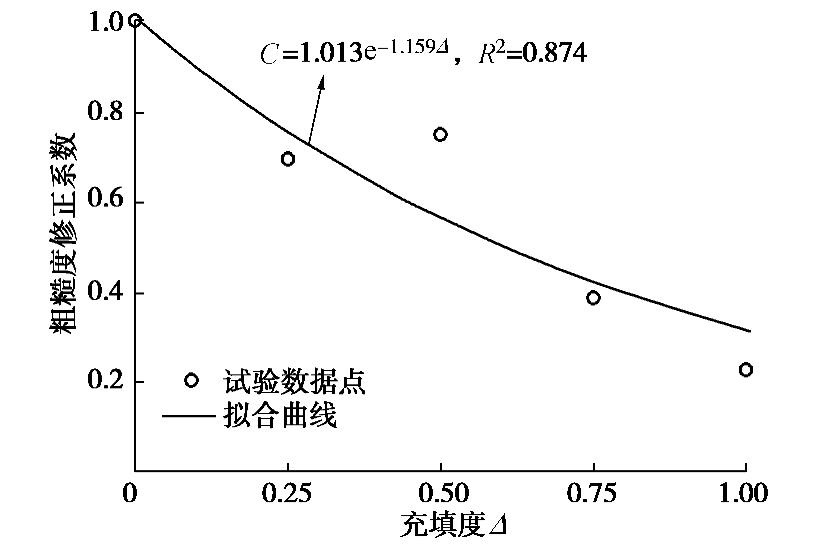
试件编号	充填度 $Δ$	峰值剪胀角d_n/(°)
试件编号	充填度 $Δ$	0.2 $σ_{c}$	0.5 $σ_{c}$	0.7 $σ_{c}$
^#1	0.00	3.552	-1.789	-3.676
	0.25	-2.310	-4.487	-4.099
	0.50	-3.239	-4.779	-4.534
	0.75	-7.480	-5.261	-5.566
	1.00	-10.772	-9.348	-10.585
^#2	0.00	2.022	-1.559	-5.333
	0.25	1.884	-3.432	-4.967
	0.50	-2.889	-3.961	-7.340
	0.75	-5.241	-4.836	-9.531
	1.00	-9.871	-7.925	-9.875
^#3	0.00	7.744	4.491	2.973
	0.25	6.141	6.197	4.986
	0.50	2.279	6.320	3.149
	0.75	-0.276	1.836	2.987
	1.00	-4.309	1.046	0.567

下载: 导出CSV

表 5 薄层充填岩石节理试件峰值剪胀角试验值

Table 5 Results of peak dilation angle of thinly-infilled rock joints

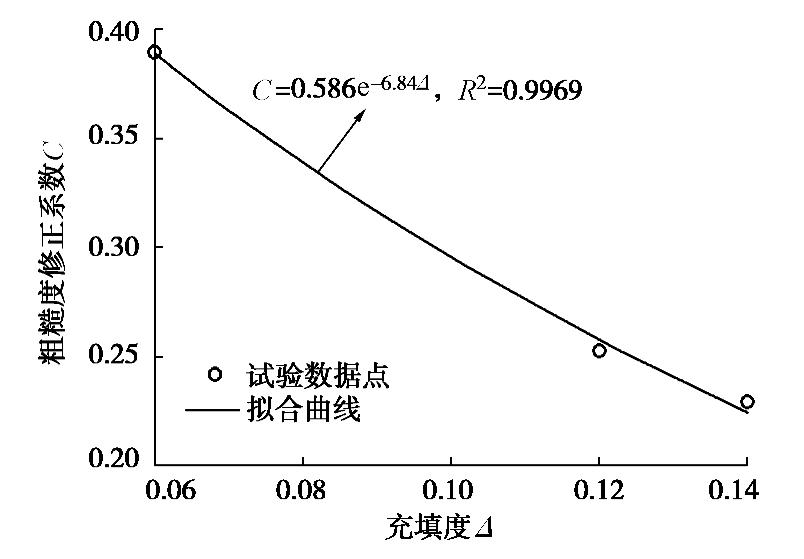
σ_n/kPa	Δ	d_nfilled
50	0.06	7.22
	0.14	4.25
	0.28	-0.15
	0.78	-1.90
	1.11	-5.25
100	0.12	3.92
	0.30	-1.53
	0.42	2.44
	0.69	-3.33
	1.11	-5.27

下载: 导出CSV

表 6 充填节理试件基本力学参数

Table 6 Mechanical parameters of infilled rock joint specimens

密度/(g·cm^-3)	单轴抗压强度/MPa	基本摩擦角/(°)	节理粗糙度JRC₀
1.85	3.5	30	10.04

下载: 导出CSV

参考文献(29)

[1]	夏才初. 工程岩体节理力学[M]. 上海: 同济大学出版社, 2002. XIA Cai-chu. Engineering Jointed Rock Mechanics[M]. Shanghai: Tongji University Press, 2002. (in Chinese)
[2]	BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics and Rock Engineering, 1977, 10(1/2): 1-54.
[3]	SCHNEIDER H J. The friction and deformation behavior of rock joints[J]. Rock Mechanics and Rock Engineering, 1976, 8(3): 169-185.
[4]	LEE Y K, PARK J W, SONG J J. Model for the shear behavior of rock joints under CNL and CNS conditions[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 70(9): 252-263.
[5]	GHAZVINIAN A H, TAGHICHIAN A, HASHEMI M, et al. The shear behavior of bedding planes of weakness between two different rock types with high strength difference[J]. Rock Mechanics and Rock Engineering, 2010, 43(1): 69-87. doi: 10.1007/s00603-009-0030-8
[6]	ASADOLLAHI P, TONON F. Constitutive. model for rock fractures Revisiting Bartons empirical model[J]. Engineering Geology 2010, 113(1/2/3/4): 11-32.
[7]	BARTON N, BANDIS S, BAKHTAR K. Strength, deformation and conductivity coupling of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics abstracts, 1985, 22(3): 121-140.
[8]	ESAKI T, DU S, MITANI Y, IKUSADA K, et al. Development of a shear-flow test apparatus and determination of coupled properties for a single rock joint[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(5): 641-650. doi: 10.1016/S0148-9062(99)00044-3
[9]	OLSSON R, BARTON N. An improved model for hydromechanical coupling during shearing of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 317-329. doi: 10.1016/S1365-1609(00)00079-4
[10]	LEE H S, CHO T F. Hydraulic characteristics of rough fractures in linear flow under normal and shear load[J]. Rock Mechanics and Rock Engineering, 2002, 35(4): 299-318. doi: 10.1007/s00603-002-0028-y
[11]	赵延林, 王卫军, 万文, 等. 节理剪胀耦合的岩体渗透特性数值研究与经验公式[J]. 煤炭学报, 2013, 38(1): 91-96. doi: 10.13225/j.cnki.jccs.2013.01.004 ZHAO Yan-lin, WANG Wei-jun, WAN Wen, et al. Numerical study of joint shear dilatation coupling seepage characteristic of rock mass and experiential formula[J]. Journal of China Coal Society, 2013, 38(1): 91-96. (in Chinese) doi: 10.13225/j.cnki.jccs.2013.01.004
[12]	赵延林, 万文, 王卫军, 等. 随机形貌岩石节理剪切–渗流数值模拟和剪胀–渗流模型[J]. 煤炭学报, 2013, 38(12): 2133-2139. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201312008.htm ZHAO Yan-lin, WAN Wen, WANG Wei-jun, et al. Shear-seepage numerical simulation and shear dilatancy- seepage model of rock joint with random morphology[J]. Journal of China Coal Society, 2013, 38(12): 2133-2139. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201312008.htm
[13]	夏才初, 喻强锋, 钱鑫, 等. 常法向刚度条件下岩石节理剪切–渗流特性试验研究[J]. 岩土力学, 2020, 41(1): 57-66. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001008.htm XIA Cai-chu, YU Qiang-feng, QIAN Xin, et al. Experimental study on shear-flow behavior of rock joints under constant normal stiffness[J]. Rock and Soil Mechanics, 2020, 41(1): 57-66. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001008.htm
[14]	BARTON N. A Review of the Shear Strength of Filled Discontinuities in Rock[R]. Oslo: Norwegian Geotechnical Institute, 1974.
[15]	PAPALIANGAS T, HENCHER S R, LUMSDEN A C, et al. The effect of frictional fill thickness on the shear strength of rock discontinuities[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(2): 81-91.
[16]	PHIEN-Wej N, SHRESTHA U B, RANTUCCI G. Effect of infill thickness on shear behaviour of rock joints[C]//Proceedings of the International Conference on Rock Joints, 1990, Loen: 289-294.
[17]	许江, 邬君宇, 刘义鑫, 等. 不同充填度下岩体剪切−渗流耦合试验研究[J]. 岩土力学, 2019, 40(9): 3416-3424, 3434. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909014.htm XU Jiang, WU Jun-yu, LIU Yi-xin, et al. Experimental study on shear-seepage of coupled properties for rock mass under different filling degrees[J]. Rock and Soil Mechanics, 2019, 40(9): 3416-3424, 3434. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909014.htm
[18]	INDRARATNA B, HAQUE A, AZIZ N. Shear behavior of idealized filled joints under constant normal stiffness[J]. Géotechnique, 1999, 49(3): 331-355. doi: 10.1680/geot.1999.49.3.331
[19]	INDRARATNA B, WELIDENIYA H S, BROWN E T. A shear strength model for idealized filled joints under constant normal stiffness[J]. Géotechnique, 2005, 55(3): 215-226. doi: 10.1680/geot.2005.55.3.215
[20]	INDRARATNA B, OLIVEIRA D A F, BROWN E T. A shear-displacement criterion for soil-filled rock discontinuities[J]. Géotechnique, 2010, 60(8): 623-633. doi: 10.1680/geot.8.P.094
[21]	INDRARATNA B, PREMADASA W, BROWN E T. Shear behaviour of rock joints with unsaturated infill[J]. Géotechnique, 2013, 63(15): 1356-1360. doi: 10.1680/geot.12.P.065
[22]	MIRZAGHORBANALI A, NEMCIK J, AZIZ N. Effects of cyclic loading on the shear behaviour of infilled rock joints under constant normal stiffness conditions[J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1373-1391. doi: 10.1007/s00603-013-0452-1
[23]	SHRIVASTAVA A K, RAO K S. Physical modeling of shear behavior of infilled rock joints under CNL and CNS boundary conditions[J]. Rock Mechanics and Rock Engineering, 2018, 51(1): 101-118. doi: 10.1007/s00603-017-1318-8
[24]	HAN G S, JING H W, JIANG Y J, et al. Effect of cyclic loading on the shear behaviours of both unfilled and infilled rough rock joints under constant normal stiffness conditions[J]. Rock Mechanics and Rock Engineering, 2020, 53(1): 31-57. doi: 10.1007/s00603-019-01866-w
[25]	International Society for Rock Mechanics Commission on Standardization of Laboratory and Field Tests. Suggested methods for the quantitative description of discontinuities in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1978, 15(6): 319-368.
[26]	李锐, 肖维民. 基于Barton标准剖面线精细数字化处理的岩石节理JRC计算新公式研究[J]. 岩石力学与工程学报, 2018, 37(增刊1): 3515-3522. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2018S1042.htm LI Rui, XIAO Wei-min. Study on a new equation for calculating JRC based on fine digitization of standard profiles proposed by Barton[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(S1): 3515-3522. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2018S1042.htm
[27]	LADANYI B, ARCHAMBAULT G. Shear strength and deformability of filled indented joints[C]//Proceedings of International Symposium on Geotechnics of Structurally Complex Formations, 1977, Capri: 317-326
[28]	土工试验方法标准：GB/T 50123—2019[S]. 2019. Standard for Geotechnical Testing Method: GB/T 50123—2019[S]. 2019. (in Chinese)
[29]	TSE R, CRUDEN D M. Estimating joint roughness coefficients[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1979, 16(5): 303-307. doi: 10.1016/0148-9062(79)90241-9

施引文献(2)

期刊类型引用(2)

1.	刘志文，王媛，董琪，高山. 不连续界面渗流的堤防防渗膜防渗效果模拟研究. 人民黄河. 2024(06): 48-53+67 . 百度学术
2.	张升，兰鹏，苏晶晶，熊海斌. 基于PINNs算法的地下水渗流模型求解及参数反演. 岩土工程学报. 2023(02): 376-383+443-444 . 本站查看