软土区双线盾构施工引起的土体变形及孔压研究

丁智; 洪哲浩; 冯丛烈; 魏新江; 徐涛; 王涛

doi:10.11779/CJGE202008011

软土区双线盾构施工引起的土体变形及孔压研究 English Version

丁智^{1, 2,},
洪哲浩¹,
冯丛烈¹,
魏新江¹,
徐涛²,
王涛³

1.
浙大城市学院土木工程系,浙江　杭州　310015
2.
澳门大学土木与环境工程系,澳门　999078
3.
中设设计集团股份有限公司,江苏　南京　210014

基金项目:

国家自然科学基金项目 51508506

浙江省自然科学基金联合基金（重点项目） LHZ20E080001

浙江省重点研发计划项目 2020C01102

杭州市科技计划项目 20191203B44

详细信息

作者简介:
丁智(1983—),男,博士,副教授,主要从事轨道交通施工及运营对周边环境影响研究方面的科研工作。E-mail：dingz@zucc.edu.cn

中图分类号: TU43
计量
- 文章访问数: 311
- HTML全文浏览量: 17
- PDF下载量: 172
出版历程
- 收稿日期: 2019-10-15
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-07-31

Soil deformation and excess pore water pressure caused by excavation of twin-bored tunnels in soft soil

1.
Department of Civil Engineering, Zhejiang University City College, Hangzhou 310015, China
2.
Department of Civil and Environmental Engineering, University of Macau, Macao 999078, China
3.
China Design Group Corporation Limited, Nanjing 210014, China

摘要

摘要: 以杭州地铁2号线某盾构区间工程为背景,推导饱和软土双线盾构掘进引起的土体变形及孔压理论解,结合实际工程参数分析土体及超孔压变化规律；控制切口附加推力、盾壳摩擦力和盾尾注浆压力的取值,研究不同施工参数对土体竖向变形的影响。结果表明：盾构接近研究断面时,施工参数对土体变形的影响较大；当双线盾构推进通过研究断面一定距离后,其施工引起的横向地表位移变化和切口附加推力作用下的超孔压变化趋于稳定；盾壳摩擦力对孔压的影响范围主要集中在盾构穿越一半长度内；当双线盾构远离研究断面后,盾尾注浆作用产生的超孔压力趋近于0；研究结果可为杭州软土区类似盾构工程提供指导建议。
- 软土 /
- 双线盾构隧道 /
- 盾构施工 /
- 土体变形 /
- 孔压变化
Abstract: The theoretical solutions for the soil deformation and excess pore water pressure caused by excavation of twin-bored tunnels in saturated soft soil are given. The data from a project of twin-bored tunnels of the Hangzhou Metro Line 2 is used to validate these solutions. The effects of additional thrust, friction between the shield and the soil and tail void grouting on the vertical deformation of the soil are investigated. It is shown that when the shield is close to the reference section, the influence of such parameters on the soil deformation is great. After the shield passing the reference section for a certain distance, the lateral displacement of the ground surface and the excess pore water pressure tend to be stable. The influence of the friction between the shield and the soil on the excess pore water pressure is limited within half the length that the shield has passed. When the shield leaves the reference section, the excess pore water pressure generated by the tail void grouting approaches 0. The research may provide guidance for future tunnel projects in similar soft soil as in Hangzhou.
- soft soil /
- twin-bored tunnel /
- shield tunneling /
- soil deformation /
- pore pressure change

HTML全文

0. 引言

在地铁隧道建设的诸多施工方法中,盾构法因施工速度较快以及对环境影响较小等特点成为首选,但其施工时仍会对周围土体产生一定程度的扰动,引起应力重分布,并在土体中产生超孔隙水压力,进而导致土体变形。一旦变形量超过警戒值,就会威胁到邻近建筑物及地下管线等结构的安全^[1]。

现有关于盾构施工引起土体变形及孔压变化的研究方法主要有实测分析法、数值模拟法和理论计算法。

（1）实测分析法

Peck^[2]、Attewell等^[3]、Mair等^[4]、Zhao等^[5]通过大量的实测数据进行反分析,验证了地表沉降槽服从正态分布理论并对沉降槽宽度系数的取值进行了统计。Chen等^[6]对杭州地铁1号线实测数据进行分析,得到土体竖直位移、深层水平位移及超孔隙压力随盾构掘进的变化规律。丁智等^[7]对软土区双线盾构施工引起的地表变形进行现场实测,分析地表变形规律及双线Peck公式在软土地区的适用性,研究土体损失率的取值。潘泓等^[8]通过动态监测小曲率半径段转弯盾构施工引起的土体分层沉降、水平位移、孔隙水压力的变化,分析了小曲率半径转弯隧道盾构掘进对紧邻土体的扰动规律。

（2）数值模拟法

Oh等^[9]通过三维有限元模拟研究盾尾注浆压力对隧道长期沉降的影响,提出了长期沉降不仅由土体损失引起还与隧道周围的土体压缩变形有关。Li等^[10]采用三维建模分析盾构隧道与周围土体的变形关系,验证了不同路径的垂直位移以及孔隙压力分布均受土层性质影响。宋锦虎等^[11]通过建立三维流固耦合模型计算了施工参数引起的隧道周围超孔压,并与现场实测值进行对比。Luo等^[12]、Li等^[13]基于Biot理论及流变力学理论建立三维流固耦合模型,并进一步预测了盾构掘进引起的土体变形与孔压变化规律。

（3）理论计算法

Sagaseta^[14]将隧道开挖所导致的土体损失等效为圆柱体,采用镜像法原理推导出地表变形计算公式。Verruijt等^[15]在Sagaseta方法基础上,采用均匀径向土体移动模型,同时考虑地层损失及椭圆变形,推导了土体变形的二维解。Loganathan等^[16]针对Verruijt解,利用Lee等^[17]提出的“间隙系数”的概念,采用更为合理的椭圆形非等量土体移动模型,得出了新的二维解。Guo等^[18]在Verruijt等^[15]的理论解基础上,考虑了地表水的分布及作用,结合等效刚度原理得到双线盾构施工引起的土体变形计算公式。魏纲等^[19]基于双线平行盾构施工中由土体损失引起的土体变形二维解推导出三维解析解,分别计算了双线盾构掘进引起的土体变形。陈春来等^[20]建立了修正的三维Peck公式,考虑了先行隧道施工对后行隧道的影响因素,计算并叠加了先后行线隧道施工引起的土体沉降。

然而以上研究大部分将土体视为单相介质,实际上土体是由固、液、气三相物质所组成,因此对于饱和土变形须考虑孔隙水压力的消散所引起的相关变形。现有关于饱和土体单圆盾构施工引起的土体变形及孔压理论解研究仅见文献[1],且缺少饱和土双线盾构掘进引起的地表变形及孔隙水压力理论计算分析及相应研究。本文以杭州地铁丰潭路站—古翠路站盾构隧道区间工程为背景,推导出饱和土双线盾构掘进引起的土体变形及孔压理论解,研究不同施工参数对土体竖向变形的影响；研究成果可为今后类似工程提供理论参考。

1. 理论解研究

1.1 假定及模型

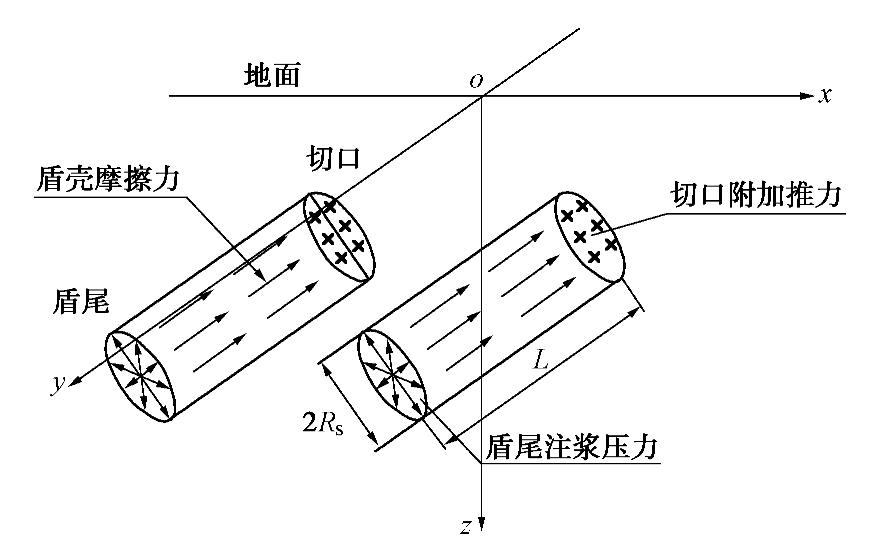
盾构在掘进时是动态变化的,且其位置变化十分复杂,为了便于理论公式推导和计算,笔者对盾构掘进过程作以下假定：①土体均质且各向同性；②假定盾构始终水平（平行于y轴）掘进；③盾构掘进过程中只考虑盾构机的切口附加推力、盾壳的摩擦力及盾尾的注浆压力影响；④盾构机切口的附加推力及盾壳的摩擦力均匀作用于掘进面及盾壳表面；⑤盾尾注浆压力沿盾尾半径方向均匀作用,且范围仅在盾构机后方1.2 m（单环管片宽度）内；⑥仅考虑盾构在半无限空间位置上的掘进变化。

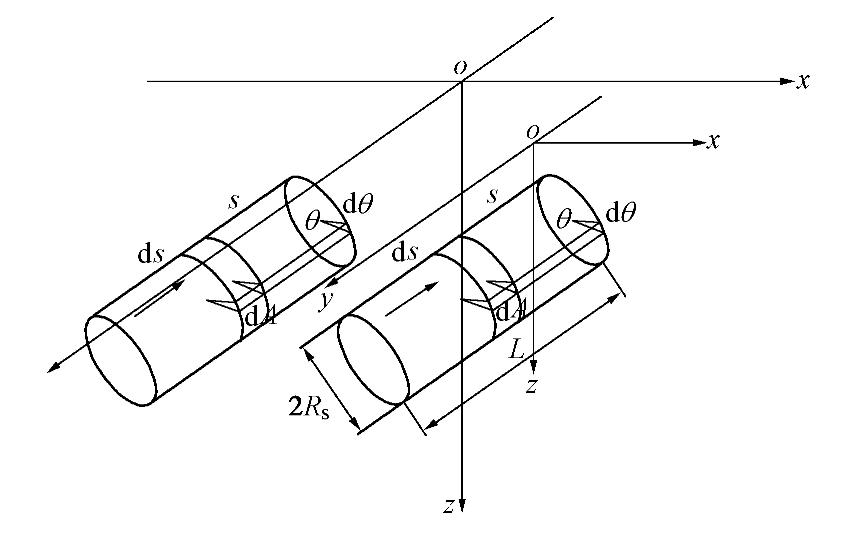
绘制双线盾构推进的力学模型如图1所示,假定图中右线隧道上的盾构机位于xoz（即y=0平面）进行开挖；左线隧道上的盾构机位于y=0平面的对称面进行开挖；左右线隧道盾构机推进方向均平行于y轴。

图 1 双线隧道盾构掘进力学模型图

Figure 1. Double-tunnel shield tunneling model

下载: 全尺寸图片幻灯片

1.2 集中力作用下土体变形和超孔压解

陈振建^[21]针对Biot固结变形,通过McNamee位移函数^[22]求解得到控制其变形的计算方程式,再使用Hankel变换^[23]推导得出土体内部某一任意点分别受到垂直及水平方向力时土体竖向变形和孔隙水压力的初始解。

土体内部h处受垂直方向力F作用的土体竖向变形为

$\begin{matrix} μ_{z v} = \frac{F}{8 π G} {\frac{r^{2} + 2 {(z - h)}^{2}}{{[r^{2} + {(z - h)}^{2}]}^{3 / 2}} + \\ \frac{2 h^{4} + 3 h^{2} r^{2} + r^{4} + 4 h z (3 h^{2} + r^{2})}{{[r^{2} + {(z + h)}^{2}]}^{5 / 2}} + \\ \frac{z^{2} (20 h^{2} + 3 r^{2}) + 12 h z^{3} + 2 z^{4}}{{[r^{2} + {(z + h)}^{2}]}^{5 / 2}}} \end{matrix}$ 。

(1)

超孔压解为

$\begin{matrix} p_{v} = \frac{F}{4 π} {- \frac{h - z}{{[r^{2} + {(z - h)}^{2}]}^{3 / 2}} + \frac{h + z}{{[r^{2} + {(z + h)}^{2}]}^{3 / 2}} + \\ \frac{2 h [- r^{2} + 2 {(h + z)}^{2}]}{{[r^{2} + {(z + h)}^{2}]}^{5 / 2}}} \end{matrix}$ 。

(2)

式中 μ_zv为垂直力作用下z方向的土体位移（m）；p_v为垂直力引起的超孔压（kPa）；G为剪切弹性模量（kPa）；r为力作用点与土体单元的水平距离（m）。

土体内部h处受水平方向力F作用土体竖向变形为

$\begin{matrix} μ_{z h} = \frac{F r \cos θ}{8 π G} {\frac{z - h}{{[r^{2} + {(z - h)}^{2}]}^{3 / 2}} + \\ \frac{z - h}{{[r^{2} + {(z + h)}^{2}]}^{3 / 2}} - \frac{6 h z (z + h)}{{[r^{2} + {(z + h)}^{2}]}^{5 / 2}}} \end{matrix}$ ；

(3)

超孔压解为

$\begin{matrix} P_{h} = \frac{F r \cos θ}{4 π} {- \frac{1}{{[r^{2} + {(z - h)}^{2}]}^{3 / 2}} - \\ \frac{1}{{[r^{2} + {(z + h)}^{2}]}^{3 / 2}} + \frac{6 h z (z + h)}{{[r^{2} + {(z + h)}^{2}]}^{5 / 2}}} \end{matrix}$ 。

(4)

式中 μ_zh为水平力作用下z方向的土体位移（m）； $P_{h}$ 为水平力引起的超孔压（kPa）；θ为力作用点与土单元连线同集中力在水平面上的夹角。

1.3 盾构施工引起的土体变形和超孔压解

丁智等^[1]基于饱和土集中力作用下土体变形和孔压解,通过积分和公式推导,提出了盾构施工引起的土体变形和超孔压解。

具体积分原理及计算公式见下：

（1）双线盾构隧道切口附加推力引起的土体变形和超孔压解

对于双线盾构隧道,其周围土体因受到盾构机切口附加推力的作用,会产生竖向变形和超孔压。其积分原理如图2所示。

图 2 切口附加推力积分示意图

Figure 2. Diagram of incision additional thrust integral

下载: 全尺寸图片幻灯片

图2中,针对切口附近任意dA,将其受到的力微分 $d F = q r d r d θ$ ,其坐标系为 $x' y' z'$ ,土体内研究点埋设深度 $h = z_{0} - r cos θ$ ,转化坐标系后代入式（3）,（4）得到土体竖向位移和超孔压的微分表达式为

$\begin{matrix} d μ_{z - q} = \frac{q r y d r d θ}{8 π G} [\frac{z + r \sin θ - z_{0}}{R_{1}^{3}} + \\ \frac{z + r \sin θ - z_{0}}{R_{2}^{3}} - \frac{6 (z_{0} - r \sin θ) z (z - r \sin θ + z_{0})}{R_{2}^{5}}] \end{matrix}$ ,

(5)

$d P_{q} = \frac{q r y d r d θ}{4 π} [- \frac{1}{R_{1}^{3}} - \frac{1}{R_{2}^{3}} + \frac{6 (z_{0} - r \sin θ) (z - r \sin θ + z_{0})}{R_{2}^{5}}],$

(6)

式中,

$\begin{array}{l} R_{1} = \sqrt{{(x - r \cos θ)}^{2} + y^{2} + {(z_{0} - r \sin θ - z)}^{2}}, \\ R_{2} = \sqrt{{(x - r \cos θ)}^{2} + y^{2} + {(z_{0} - r \sin θ + z)}^{2}}, \end{array}}$

(7)

式中,q为切口附加推力（kN/m²）,μ_z-q为土体在q作用下的竖直方向位移（m）,P_q为土体在q作用下的超孔压（kPa）,z₀为隧道轴线埋深（m）,R_s为盾构开挖半径（m）。

将式（5）,（6）进行积分可得到q引起的任意点（x,y,z）的土体变形和超孔压解：

$μ_{z - q} = \int_{0}^{2 π} \int_{0}^{R_{s}} d μ_{z - q}$ ,

(8)

$P_{q} = \int_{0}^{2 π} \int_{0}^{R_{s}} d P_{q}$ 。

(9)

（2）双线盾构隧道盾壳摩擦力引起的土体变形和超孔压解

双线盾构隧道盾壳与土体之间的摩擦力f引起的土体位移和超孔压与切口附加推力q类似,其原因是q和f均为平行于y轴方向上的力。其积分原理见图3。

图 3 盾壳摩擦力积分示意图

Figure 3. Diagram of shield shell friction integral

下载: 全尺寸图片幻灯片

图3中,ds是盾壳上任一微元体,将其受到的力微分 $d F = f R_{s} d s d θ$ ,土体内部研究点位于 $x^{'} y^{'} z^{'}$ 坐标轴内,埋设深度 $h = z_{0} - r cos θ$ ,转化坐标系后代入式（3）,（4）得到土体竖向位移和超孔压的微分表达式为

$\begin{matrix} d μ_{z - f} = \frac{f R_{s} (y - s) d s d θ}{8 π G} \cdot \\ [\frac{z + R_{s} \sin θ - z_{0}}{R_{1}^{3}} + \frac{z + R_{s} \sin θ - z_{0}}{R_{2}^{3}} - \\ \frac{6 (z_{0} - R_{s} \sin θ) z (z - R_{s} \sin θ + z_{0})}{R_{2}^{5}}] \end{matrix}$ ,

(10)

$\begin{matrix} d P_{f} = \frac{f R_{s} (y - s) d s d θ}{4 π} [- \frac{1}{R_{1}^{3}} - \frac{1}{R_{2}^{3}} + \\ \frac{6 (z_{0} - R_{s} \sin θ) (z - R_{s} \sin θ + z_{0})}{R_{2}^{5}}] \end{matrix}$ ,

(11)

式中,

$\begin{array}{l} R_{1} = \sqrt{{(x - R_{s} \cos θ)}^{2} + {(y - s)}^{2} + {(z_{0} - R_{s} \sin θ - z)}^{2}}, \\ R_{2} = \sqrt{{(x - R_{s} \cos θ)}^{2} + {(y - s)}^{2} + {(z_{0} - R_{s} \sin θ + z)}^{2}}, \end{array}}$

(12)

式中,f为盾壳摩擦力（kN/m²）,μ_z-f为土体在f作用下的竖直方向位移（m）,P_f为土体在f作用下的超孔压（kPa）,L为盾构机长度（m）。

将式（10）,（11）进行积分可得到f引起的任一研究点（x,y,z）的土体变形和超孔压解：

$μ_{z - f} = \int_{0}^{2 π} \int_{0}^{L} d μ_{z - f}$ ,

(13)

$P_{f} = \int_{0}^{2 π} \int_{0}^{L} d P_{f}$ 。

(14)

（3）双线盾构隧道盾尾注浆压力引起的土体变形和超孔压解

双线盾构隧道在同步注浆时产生的压力p可按竖直方向和水平方向分解为p_v和p_h,由于受到p_h作用下土体产生的竖向位移相较于p_v作用下很小,故在积分时不将p_h纳入盾尾注浆压力中而用p_v的值来代替盾尾注浆压力。积分原理如图4所示。

图 4 盾尾注浆压力积分示意图

Figure 4. Diagram of shield tail grouting pressure integral

下载: 全尺寸图片幻灯片

针对盾尾处任意微元体dA,将其受到的力微分dF=pR_sdsdθ（F_h微分为dF_h=pR_scosθdsdθ,F_v微分为dF_v=pR_ssinθdsdθ）,土体内部研究点其坐标位于坐标轴内,埋设深度h=z₀-rcosθ,转化坐标系后代入式（1）,（2）得到土体竖向位移和超孔压的微分表达式为

(15)

$\begin{array}{l} d P_{p_{v}} = \frac{p_{v} R_{s} s i n θ d s d θ}{4 π} {- \frac{z - R_{s} \sin θ - z_{0}}{R_{1}^{3}} + \frac{z - R_{s} \sin θ + z_{0}}{R_{2}^{3}} + \\ \frac{2 (z_{0} - R_{s} \sin θ) [{(x - R_{s} \cos θ)}^{2} + {(y - L - s)}^{2} - 2 {(z_{0} - R_{s} \sin θ + z)}^{2}]}{R_{2}^{5}}}, \end{array}$

(16)

式中,

$\begin{array}{l} R_{1} = \sqrt{{(x - R_{s} \cos θ)}^{2} + {(y - L - s)}^{2} + {(z_{0} - R_{s} \sin θ - z)}^{2}}, \\ R_{2} = \sqrt{{(x - R_{s} \cos θ)}^{2} + {(y - L - s)}^{2} + {(z_{0} - R_{s} \sin θ + z)}^{2}}, \end{array}}$

(17)

式中 p_v为盾尾注浆压力竖直分力（kN/m²）； $μ_{z - p_{v}}$ 为土体在p_v作用下的竖直方向位移（m）； $p_{p_{v}}$ 为土体在p_v作用下的超孔压（kPa）；M为盾构机单环长度（m）。

将公式（15）,（16）进行积分可得到p引起的任一研究点（x,y,z）的土体变形和超孔压解：

$μ_{z - p_{v}} = \int_{0}^{2 π} \int_{0}^{M} d μ_{z - p_{v}}$ ,

(18)

$P_{p_{v}} = \int_{0}^{2 π} \int_{0}^{M} d P_{p_{v}}$ 。

(19)

（4）双线盾构隧道土体损失引起的土体变形

Sagaseta^[14]提出了地表在周围土体损失的情况下会产生变形：

$s_{z_{f}} = \frac{V_{s_{f}}}{2 π} \frac{z_{0}}{x^{2} + z_{0}^{2}} [1 + \frac{y}{\sqrt{x^{2} + y^{2} + z_{0}^{2}}}]$ ,

(20)

$s_{z_{t}} = \frac{V_{s_{t}}}{2 π} \frac{z_{0}}{x^{2} + z_{0}^{2}} [1 + \frac{y - L}{\sqrt{x^{2} + {(y - L)}^{2} + z_{0}^{2}}}]$ ,

(21)

式中, $s_{z_{f}}$ 为在土体损失影响下土体产生的竖向位移, $s_{z_{t}}$ 为在盾尾间隙影响下土体产生的竖向位移, $V_{s_{f}}$ , $V_{s_{t}}$ 为开挖面与盾尾的地层损失。

2. 现场工程及地质条件

2.1 工程概况

本文以丰潭路站—古翠路站盾构区间实际工程为依托,工程概况如下：丰古区间主体位于杭州市西湖区,双线隧道线路呈东西向敷设,总长度为1007.25 m,其中上行线全长503.386 m,下行线全长503.866 m,埋深为7.78～9.66 m。上、下行线盾构施工均采用日本石川岛土压平衡盾构,其外径D_s=6.34 m,主机长L=8.58 m。隧道衬砌结构为装配式钢筋混凝土管片,采用错缝拼接,纵向及环向均采用高强度抗弯螺栓连接,管片内径5.5 m,外径6.2 m,环宽1.2 m,厚0.35 m。

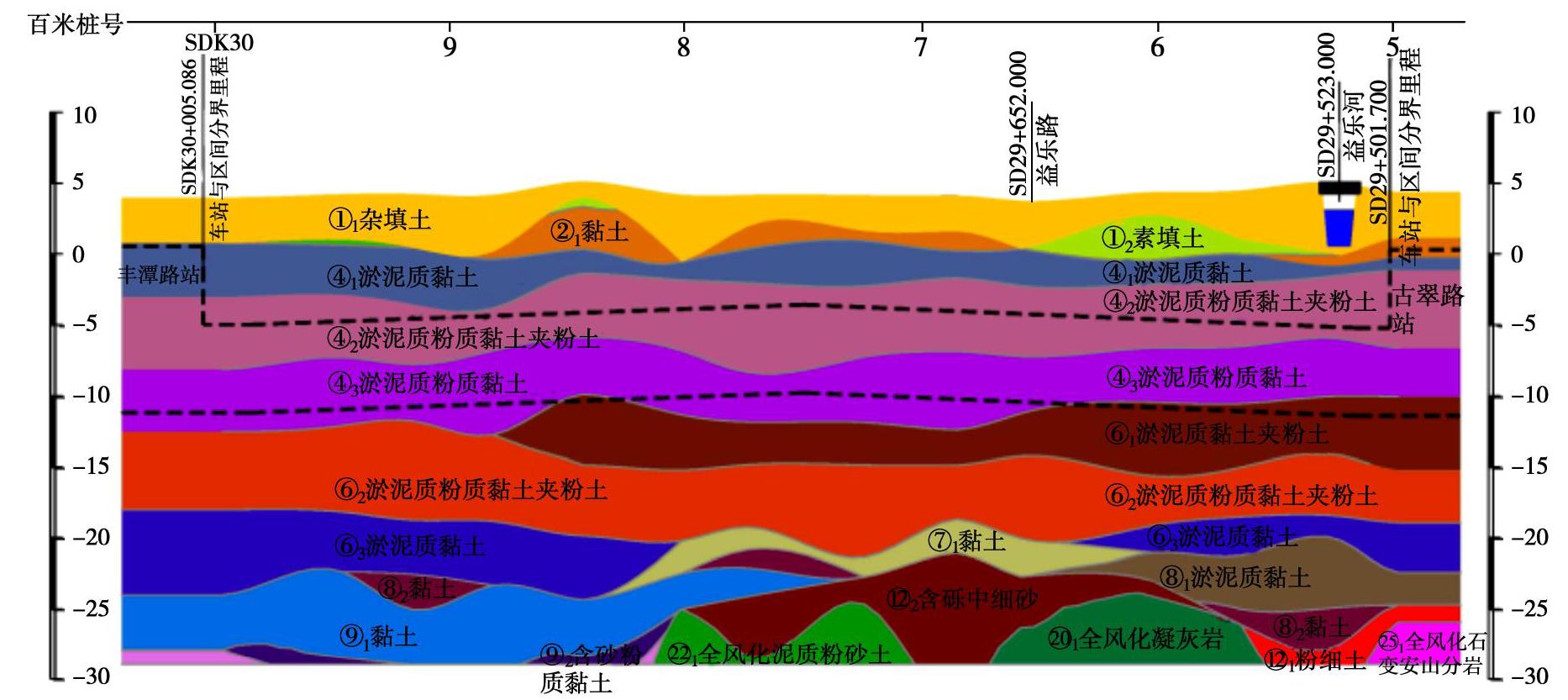
2.2 地质条件

本试验研究对象盾构下穿地质剖面如图5所示。盾构主要穿越土层如下：①₁杂填土,①₂素填土,②₁黏土,④₁淤泥质黏土,④₂淤泥质粉质黏土夹粉土,④₃淤泥质粉质黏土,⑥₁淤泥质黏土夹粉土。本试验盾构下穿均为软弱地层,具有低强度、低渗透性、高压缩性的特点,场地主要土层的物理力学参数如表1。

图 5 盾构掘进地质剖面示意图

Figure 5. Schematic diagram of shield underlying geological section

下载: 全尺寸图片幻灯片

表 1 各层土体参数

Table 1. Parameters of soil strata

主要土层	含水率w/%	重度γ/(kN·m^-3)	黏聚力c/kPa	内摩擦角φ/(°)	压缩模量E_S/MPa
①₁杂填土	—	18.0	8.0	12.0	3.0
①₁素填土	—	18.5	10.0	10.0	2.5
②₁黏土	33.7	18.0	12.0	14.0	4.5
④₁淤泥质黏土	46.0	17.6	7.0	13.0	1.6
④₁淤泥质粉质黏土夹粉土	36.5	18.3	8.0	20.0	3.5
④₁淤泥质粉质黏土	42.1	18.0	9.0	15.0	3.0
⑥₁淤泥质黏土夹粉土	40.1	17.8	12.0	16.0	3.8

下载: 导出CSV

| 显示表格

3. 计算结果分析

3.1 参数取值

盾构掘进过程中,切口附加推力q、盾壳摩擦力f以及盾尾注浆压力p的取值方法如下。

将盾构掘进至开挖面轴线时的压力值与这一位置的土压力初始设定值（水平方向平行于y轴）的差作为切口附加推力q。

盾壳摩擦力f为

$f = \frac{1 + K_{0}}{2} u R_{s} Z_{0}$ ,

(22)

式中,μ为盾壳与周围土体间摩擦产生的摩擦力系数,取值见文献[24],K₀为静止土压力系数,R_s为盾构半径（m）,Z₀为隧道轴线埋深（m）。

盾构通过后由于盾尾与土体存在一定的空隙,会使周围土体出现应力释放,逐渐向隧道轴线方向移动,进而产生变形。考虑释放的应力影响后,采用下述公式对盾尾注浆压力p进行取值：

$p = p_{g} - 0.3 σ_{0}$ ,

(23)

式中,p_g为实际注浆压力（kPa）, $σ_{0}$ 为注浆处土压力初始值（kPa）。

本文以监测断面SD160为研究断面,计算时所需参数数值：盾构半径R_s=3.1 m；盾构机长度L=8.58 m；土体剪切模量G=4 MPa；隧道轴线埋深Z₀=12.76 m。采用上述的计算方法得到的3种施工参数数值分别为：盾壳摩擦力f=39.35 kPa；切口附加推力q=75.07 kPa；盾尾注浆压力p=226.32 kPa。

3.2 地表变形分析

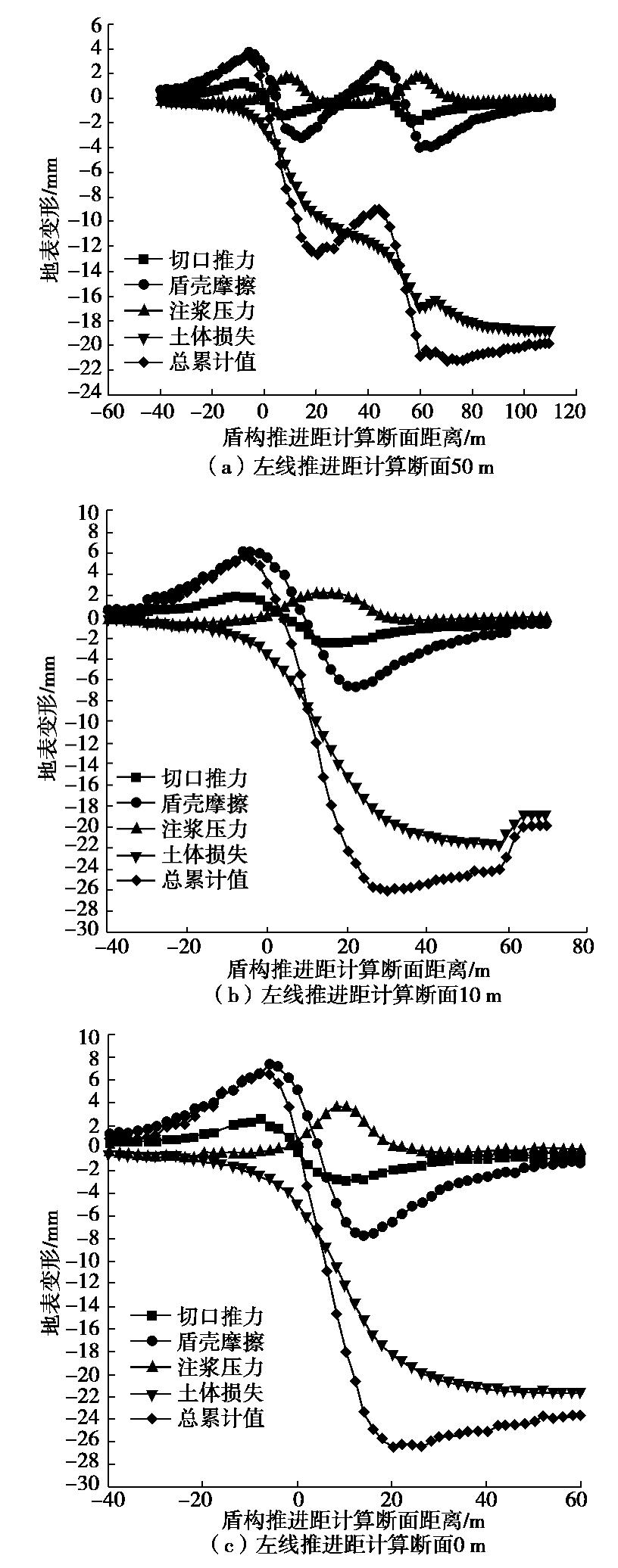
地表变形计算结果如图6（a）～（c）所示。随着左线距计算断面越近,在切口附加推力q、盾壳摩擦力f、盾尾注浆压力p、土体损失 $V_{s}$ 各参数作用下双线盾构施工引起的地表变形逐渐增加。当左线距计算断面0 m时,由切口附加推力q引起的地表隆起和沉降最大值为左线距计算断面50 m时的2.12倍和1.66倍；由盾壳摩擦力f引起的地表隆起和沉降最大值分别为左线距计算断面50 m时的1.97倍和1.96倍；由盾尾注浆压力p引起的地表隆起和沉降最大值为左线距计算断面50 m时的2.21倍和1.44倍；由土体损失 $V_{s}$ 引起的地表沉降最大值为左线距计算断面50 m时的1.15倍；总累计值为左线距计算断面50 m时的1.25倍。地表变形在左线未到达计算断面时,均出现了双峰的形状,其原因是左右线掘进均对周围土体产生扰动,而由于左线为后行线,土体在二次扰动的作用下,其峰值要大于右线。

图 6 双线盾构施工引起的纵向地表变形

Figure 6. Deformations of longitudinal surface caused by double-shield construction

下载: 全尺寸图片幻灯片

结合图6（c）分析,当双线盾构推进至距研究断面0 m（即刚好掘进至研究断面所在环号）时,切口附加推力q施工引起的地表变形关于纵轴呈反对称形状。盾构切削处地表为隆起状态,隆起峰值出现在双线盾构到达前9 m处,为2.7 mm；盾壳摩擦力f施工引起的地表变形关于SD160断面呈反对称形状,左半部分为隆起,右半部分为沉降,且隆起与沉降的峰值相同,均为7.5 mm；切口附加推力q施工引起的地表变形整体呈隆起状态,其隆起变形关于横轴y=10呈对称形状,隆起峰值出现在双线盾构距研究断面9.5 m处,为4 mm。当双线盾构推进至距研究断面距离超过10 m时,在切口附加推力q和盾壳摩擦力f作用下地表变形较大,且切口附加推力q作用下的地表变形量约为盾壳摩擦力f作用下的1/2。双线盾构推进距研究断面距离超过20 m后,地表在切口附加推力q和盾壳摩擦力f作用下产生的沉降出现回弹现象（这一阶段受同步注浆影响）,最终趋于稳定,而从图中可以看出该时段的地表变形主要是由土体损失引起的。

且如图6（a）～（c）所示,在双线盾构隧道掘进过程中,地表隆起主要由盾构机摩擦力、开挖面附加推力以及盾尾注浆压力过大所导致,且盾壳摩擦力占比较大；地表沉降主要由盾尾土体损失所导致,因此在实际施工中可根据盾构机推进位置不同分阶段控制施工参数,进而控制相应地表变形。尤其在双线盾构机尾部,应严格控制盾构管片形状及保证盾尾注浆压力的稳定,提高管片拼装精度避免管片产生脱离现象,尽可能减小盾尾土体损失。

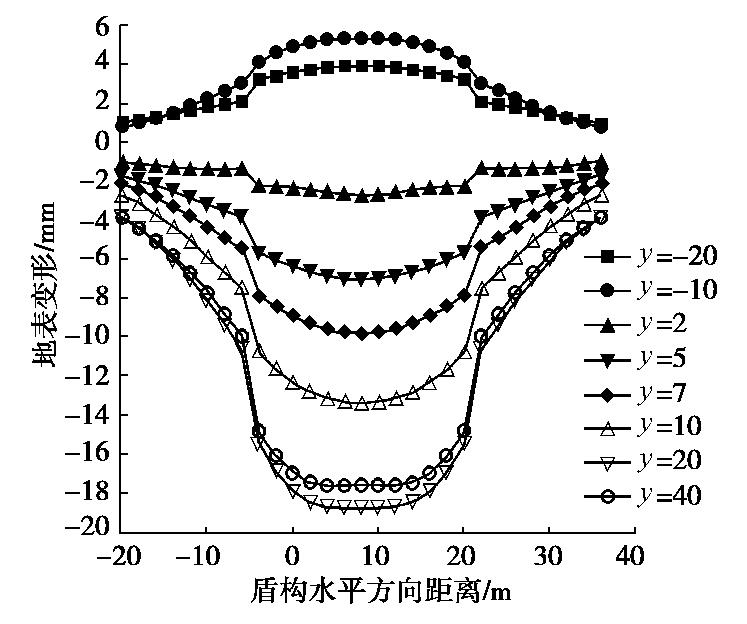
图7表明双线盾构施工参数引起的横向地表位移,随着盾构距研究断面距离的增大而增大。地表横向变形峰值出现在y=20时,为18.67 mm。当双线盾构未掘进至SD160断面时,施工引起的横向地表位移为隆起变形,通过时横向地表变形迅速发展为沉降。当双线盾构推进至研究断面20 m后,其引起的横向地表位移稳定在-19 mm左右。这与文献[6,7,25]的实测数据变化规律基本一致：当盾构掘进至测点4R_s～6 R_s时,地面出现隆起变形；盾构机通过测点下方时,地面开始产生沉降变形；盾尾远离测点约3R_s～4R_s后,地面沉降达到瞬时沉降的峰值；且随着时间的增加受扰动的土体会产生排水固结,地面又逐渐开始产生一定程度的沉降变形。这也验证了本文理论解的正确性。且和单线盾构隧道相比,双线平行隧道掘进引起的沉降槽宽度明显增加,但地表沉降曲线仍呈对称性,这主要是由于本文左、右线土体损失取相同值的原因所致。

图 7 双线盾构施工引起的横向地表变形

Figure 7. Deformations of lateral surface caused by double-shield construction

下载: 全尺寸图片幻灯片

3.3 超孔隙水压力分析

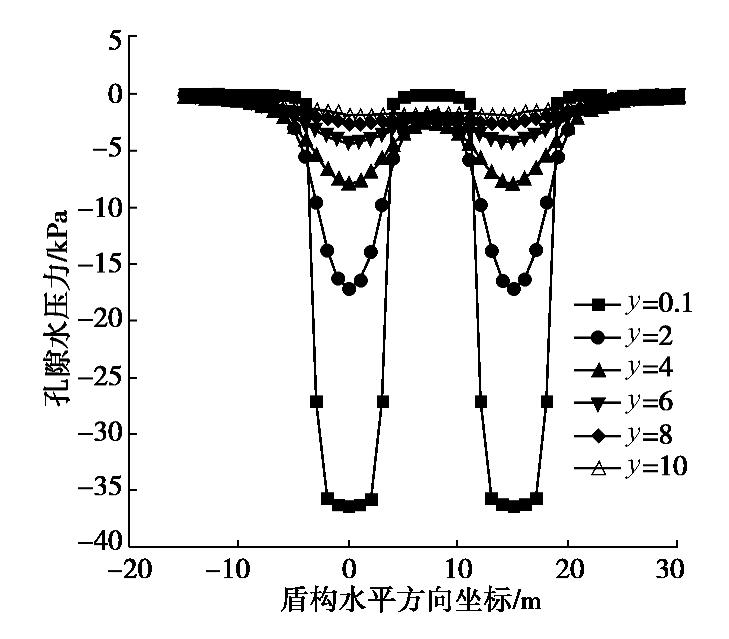
分析图8可得,双线盾构施工切口附加推力引起的水平轴线孔压曲线关于横坐标L=8.5 m（即盾构机长度）呈对称形状。双线盾构施工中切口附加推力q产生的孔压值随着盾构离研究断面的距离增加而迅速下降。当盾构刚离开SD160断面0.1m时,切口附加推力q作用下产生的孔压为36 kPa,当盾构距研究断面为2 m时,切口附加推力q作用下产生的孔压下降到17 kPa。由此可见盾构刚离开时对孔压变化的影响较大。当双线盾构通过研究断面4 m后,切口附加推力q作用下的孔压变化趋于稳定。

图 8 双线盾构施工切口附加推力引起的水平轴线孔压变化

Figure 8. Variation of horizontal axis pore pressure caused by additional thrust of double-shield construction

下载: 全尺寸图片幻灯片

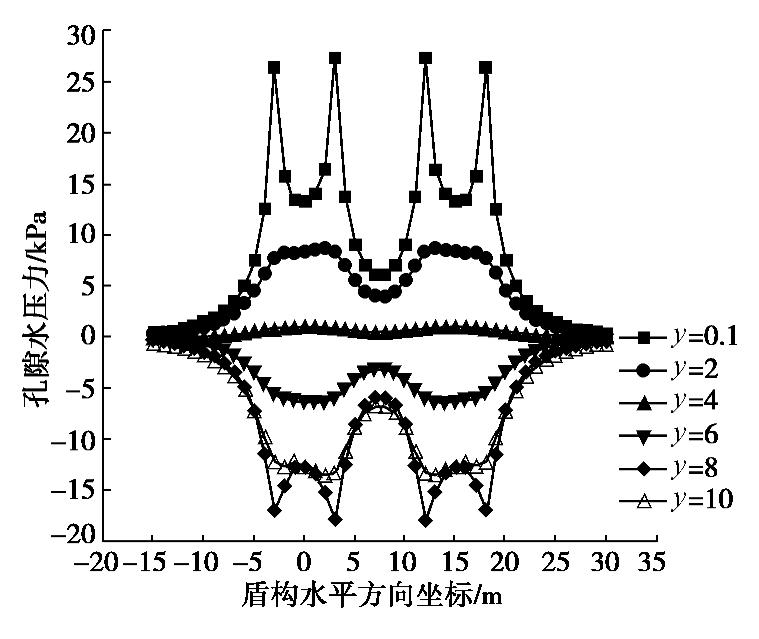
由图9可知,双线盾构施工盾壳摩擦力引起的水平轴线孔压曲线同样呈对称分布,其峰值出现在盾构推进至测点的位置。对于在双线盾构施工中盾壳摩擦力f作用下产生的孔压,当盾构距SD160断面为4 m即大约是盾构机长度的1/2时,其对应的曲线在图中近似为一条水平线,其原因是研究断面左右孔压相抵消,而双线盾构在掘进时有水平距离,故叠加后呈对称形状,整体孔隙水压力数值近似为0。并且在盾壳摩擦力f作用下产生的孔压影响范围主要集中在盾构穿越一半长度的±4 m内。

图 9 双线盾构施工盾壳摩擦力引起的水平轴线孔压变化

Figure 9. Variation of horizontal axis pore pressure caused by friction of shield shell of double-line shield construction

下载: 全尺寸图片幻灯片

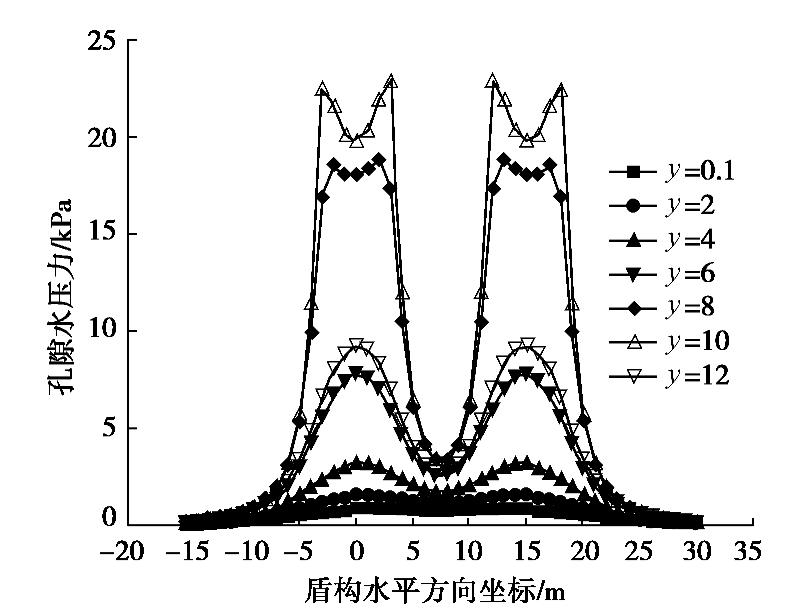
观察图10可得其曲线关于横坐标L=8.5 m（即盾构机长度）呈现对称分布,这一规律与之前曲线类似,符合双线平行隧道的特点。针对双线盾构施工中盾尾注浆压力p作用下产生的孔压,当盾构距断面6 m后,因p作用产生的孔压迅速增大,而当盾构距断面12 m后,p作用产生的孔压力数值基本稳定降至0。

图 10 双线盾构施工盾尾注浆压力引起的水平轴线孔压变化

Figure 10. Variation of horizontal axis pore pressure caused by grouting pressure at shield tail of double-line shield construction

下载: 全尺寸图片幻灯片

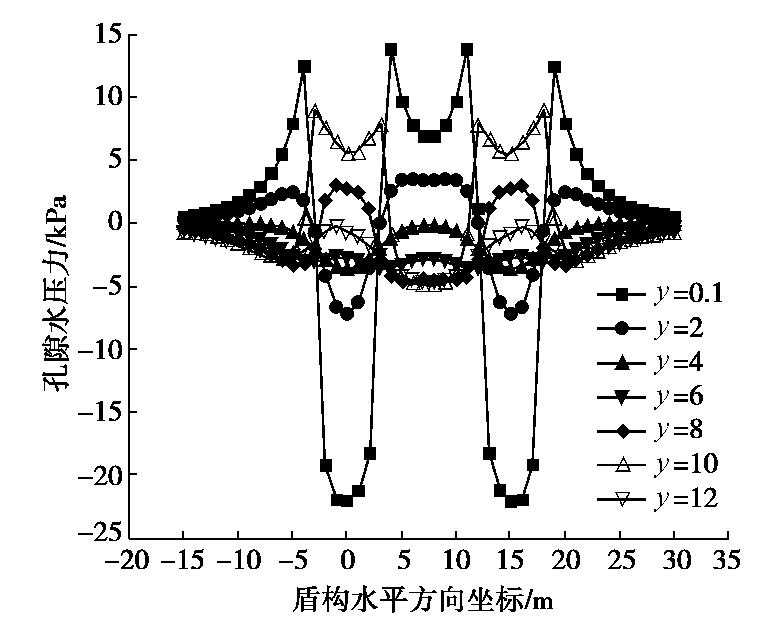
将由切口附加推力q、盾壳摩擦力f和盾尾注浆压力p作用产生的孔压值叠加,绘制孔压累计变化曲线如图11。分析可知,双线盾构开挖引起的孔压峰值主要出现在盾构刚到达和刚离开研究断面时。切口附加推力q和盾壳摩擦力f是盾构未推进至研究断面前孔压变化的主要影响因素,盾尾注浆压力p和盾壳摩擦力f是盾构离开研究断面后孔压变化的主要影响因素。由此可在盾构掘进中分阶段控制施工参数,保证孔隙水压力值不出现异常变化。

图 11 双线盾构3种施工参数引起的水平轴线孔压累计变化

Figure 11. variation of horizontal axis pore pressure caused by three construction parameters of double-line shield

下载: 全尺寸图片幻灯片

且由图8～11理论分析结果可知,双线盾构施工引起的土体超孔隙水压力变化可分为4个阶段：①盾构机刀盘接近前,会产生比较大的负孔压,主要原因是切口附近的土体向盾构隧道内涌入,而外围的水却补给不及时所导致,即刀盘切削土体时产生卸荷作用出现负的孔压。②刀盘通过后至R_s距离期间,土体受盾构机施工的挤压作用及机身摩擦力作用,孔压值明显增加。③盾尾临近时,受到补偿注浆压力的作用,孔压值再次升高。④盾尾通过后,由于盾尾空隙的影响,孔压值会产生明显下降的现象。这与文献[8]的孔压实测变化规律基本吻合,这也进一步验证了本文理论解的正确性。

4. 结论

（1）左线盾构距计算断面越近,施工参数对地表变形的影响也就越大,由开挖面附加推力、盾构机身摩擦力及盾尾注浆压力引起的地表变形在左线未到达计算断面时,均出现了双峰的形状。

（2）双线盾构到达前,横向地表位移以隆起为主,通过时迅速向沉降发展,盾尾通过一定距离后达到瞬时沉降的峰值,且沉降槽宽度相比单线隧道明显增加。

（3）盾壳摩擦力作用的孔压影响范围主要集中在盾构穿越一半长度的±4 m内；当双线盾构通过研究断面4 m后,切口附加推力引起的孔压变化趋于稳定；当双线盾构距计算断面12 m后,由盾尾注浆压力产生的孔压力数值趋近于0。

（4）双线盾构施工引起的土体超孔隙水压力响应可分为4个阶段,包括刀盘接近前、刀盘通过后开始至通过一定距离期间、盾尾临近时以及盾尾通过后。

限于篇幅,关于双线盾构隧道掘进距离不一致、左右线土体损失取不同值以及不同直径盾构掘进引起的土体变形及孔压分布规律将另撰文分析。

图 1 双线隧道盾构掘进力学模型图

Figure 1. Double-tunnel shield tunneling model

下载: 全尺寸图片幻灯片

图 2 切口附加推力积分示意图

Figure 2. Diagram of incision additional thrust integral

下载: 全尺寸图片幻灯片

图 3 盾壳摩擦力积分示意图

Figure 3. Diagram of shield shell friction integral

下载: 全尺寸图片幻灯片

图 4 盾尾注浆压力积分示意图

Figure 4. Diagram of shield tail grouting pressure integral

下载: 全尺寸图片幻灯片

图 5 盾构掘进地质剖面示意图

Figure 5. Schematic diagram of shield underlying geological section

下载: 全尺寸图片幻灯片

图 6 双线盾构施工引起的纵向地表变形

Figure 6. Deformations of longitudinal surface caused by double-shield construction

下载: 全尺寸图片幻灯片

图 7 双线盾构施工引起的横向地表变形

Figure 7. Deformations of lateral surface caused by double-shield construction

下载: 全尺寸图片幻灯片

图 8 双线盾构施工切口附加推力引起的水平轴线孔压变化

Figure 8. Variation of horizontal axis pore pressure caused by additional thrust of double-shield construction

下载: 全尺寸图片幻灯片

图 9 双线盾构施工盾壳摩擦力引起的水平轴线孔压变化

Figure 9. Variation of horizontal axis pore pressure caused by friction of shield shell of double-line shield construction

下载: 全尺寸图片幻灯片

图 10 双线盾构施工盾尾注浆压力引起的水平轴线孔压变化

Figure 10. Variation of horizontal axis pore pressure caused by grouting pressure at shield tail of double-line shield construction

下载: 全尺寸图片幻灯片

图 11 双线盾构3种施工参数引起的水平轴线孔压累计变化

Figure 11. variation of horizontal axis pore pressure caused by three construction parameters of double-line shield

下载: 全尺寸图片幻灯片

表 1 各层土体参数

Table 1 Parameters of soil strata

主要土层	含水率w/%	重度γ/(kN·m^-3)	黏聚力c/kPa	内摩擦角φ/(°)	压缩模量E_S/MPa
①₁杂填土	—	18.0	8.0	12.0	3.0
①₁素填土	—	18.5	10.0	10.0	2.5
②₁黏土	33.7	18.0	12.0	14.0	4.5
④₁淤泥质黏土	46.0	17.6	7.0	13.0	1.6
④₁淤泥质粉质黏土夹粉土	36.5	18.3	8.0	20.0	3.5
④₁淤泥质粉质黏土	42.1	18.0	9.0	15.0	3.0
⑥₁淤泥质黏土夹粉土	40.1	17.8	12.0	16.0	3.8

下载: 导出CSV

参考文献(25)

[1]	丁智, 王凡勇, 魏新江, 等. 饱和土盾构施工引起的三维土体变形及孔隙水压力研究[J]. 岩石力学与工程学报, 2018, 37(9): 2189-2199. doi: 10.13722/j.cnki.jrme.2018.0356 DING Zhi, WANG Fan-yong, WEI Xin-jiang, et al. Three-dimensional deformation and pore pressure caused by shield construction in saturated soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(9): 2189-2199. (in Chinese) doi: 10.13722/j.cnki.jrme.2018.0356
[2]	PECK R B. Deep excavations and tunneling in soft ground[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, 1969, Mexico: 225-281.
[3]	ATTEWELL P B, FARMER I W. Ground deformations resulting from shield tunnelling in london clay[J]. Canadian Geotechnical Journal, 1974, 11(3): 380-395. doi: 10.1139/t74-039
[4]	MAIR R J, TAYLOR R N, BRACEGIRDLEA . Subsurface settlement profiles above tunnels in clays[J]. Géotechnique, 1993, 43(2): 315-320. doi: 10.1680/geot.1993.43.2.315
[5]	ZHAO W, JIA P, ZHU L, et al. Analysis of the additional stress and ground settlement induced by the construction of double-o-tube shield tunnels in sandy soils[J]. Applied Sciences, 2019, 9(7): 1399. doi: 10.3390/app9071399
[6]	CHEN R P, ZHU J, LIU W, et al. Ground movementinduced by parallel EPB tunnels in silty soils[J]. Tunnelling and Underground Space Technology, 2011, 26(1): 163-171.
[7]	丁智, 王凡勇, 魏新江. 软土双线盾构施工地表变形实测分析与预测[J]. 浙江大学学报(工学版), 2019, 53(1): 66-73. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201901007.htm DING Zhi, WANG Fan-yong, WEI Xin-jiang. Prediction and analysis of surface deformation caused by twin shield construction in soft soil[J]. Journal of Zhejiang University (Engineering Science Edition), 2019, 53(1): 66-73. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201901007.htm
[8]	潘泓, 苏文渊, 翟国林, 等. 小曲率半径转弯隧道盾构施工扰动实测分析[J]. 岩石力学与工程学报, 2017, 36(4): 1024-1031. doi: 10.13722/j.cnki.jrme.2016.0869 PAN Hong, SU Wen-yuan, HUO Guo-lin, et al. Soil disturbance induced by shield advancing through a small radius path[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(4): 1024-1031. (in Chinese) doi: 10.13722/j.cnki.jrme.2016.0869
[9]	OH J Y, PARK H, KIM D, et al. Study on the effect of tail void grouting on the short-and long-term surface settlement in the shield TBM Tunneling using numerical analysis[J]. Journal of Korean Tunnelling and Underground Space Association, 2017, 19(2): 265-281. doi: 10.9711/KTAJ.2017.19.2.265
[10]	LI Y, CUI Z D, TAN J. Numerical simulation of longitudinal settlement of shield tunnel in the coastal city Shanghai[J]. Marine Georesources & Geotechnology, 2017, 35(3): 365-370.
[11]	宋锦虎, 缪林昌, 戴仕敏, 等. 盾构施工对孔压扰动的三维流固耦合分析[J]. 岩土工程学报, 2013, 35(2): 302-312. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201302016.htm SONG Jin-hu, MIAO Lin-chang, DAI Shi-min, et al. 3D coupled mechanical and hydraulic analysis of pore water pressure disturbed by shield tunnelling[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 302-312. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201302016.htm
[12]	LUO Z J, LI Z, TAN J, et al. Three-dimensional fluid–soil full coupling numerical simulation of ground settlement caused by shield tunneling[J]. European Journal of Environmental and Civil Engineering, 2018, 26(1): 1-15.
[13]	LI Z, LUO Z J, XU C H, et al. 3D fluid-solid full coupling numerical simulation of soil deformation induced by shield tunneling[J]. Tunnelling and Underground Space Technology, 2019, 90(8): 174-182.
[14]	SAGASETA C. Analysis of undrained soil deformation due to ground loss[J]. Géotechnique, 1987, 37(3): 301-320. doi: 10.1680/geot.1987.37.3.301
[15]	VERRUIJT A, BOOKER J. R. Surface settlement due to deformation of a tunnel in an elastic half plane[J]. Géotechnique, 1996, 46(4): 753-756 doi: 10.1680/geot.1996.46.4.753
[16]	LOGANATHAN N, POULOS H G. Analysis prediction for tunneling-induced ground movement in clays[J]. Journal of Geotechnicaland Geo-environmental Engineering, 1998, 124(9): 846-856. doi: 10.1061/(ASCE)1090-0241(1998)124:9(846)
[17]	LEE K M, ROWE R K, LO K Y. Subsidence owing to tunneling(I): estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 29(6): 929-940. doi: 10.1139/t92-104
[18]	GUO C X, GUAN X M, SHI LL, et al. The influence of earth pressure balanced shield tunnel underpassing coastal water body on stratum deformation[J]. Journal of Coastal Research, 2018, 83(S0): 237-246.
[19]	魏纲, 庞思远. 双线平行盾构隧道施工引起的三维土体变形研究[J]. 岩土力学, 2014, 35(9): 2562-2568. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201409020.htm WEI Gang, PANG Si-yuan. Study of three-dimensional soil deformation caused by double-line parallel shield tunnel construction[J]. Rock and Soil Mechanics, 2014, 35(9): 2562-2568. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201409020.htm
[20]	陈春来, 赵城丽, 魏纲, 等. 基于Peck公式的双线盾构引起的土体沉降预测[J]. 岩土力学, 2014, 35(8): 2212-2218. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201408013.htm CHEN Chun-lai, ZHAO Cheng-li, WEI Gang, et al. Prediction of soil settlement induced by double-line shield tunnel based on peck formula[J]. Rock and Soil Mechanics, 2014, 35(8): 2212-2218. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201408013.htm
[21]	陈振建. 半无限饱和土内部作用集中力的初值解[J]. 水利水运科学研究, 2000(2): 33-38. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY200002006.htm CHEN Zhen-jian. Initial solution of semi-infinite saturated soil loaded by internal concentrated force[J]. Journal of Nanjing Hydraulic Research Institute, 2000(2): 33-38. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY200002006.htm
[22]	MCNAMME J, GIBSON R E. Displacement function and linear transform applied to diffusion through porous elastic media[J]. Quarterly Journal of Mechanics and Applied Mathematics, 1960, 13(1): 98-111.
[23]	SNEDDON I N. Fourier Transforms[M]. New York: McGraw-Hill, 1951: 52-57.
[24]	许宏发, 吴华杰, 郭少平, 等. 桩土接触面单元参数分析[J]. 探矿工程(岩土钻掘工程), 2002(5): 10-12. https://www.cnki.com.cn/Article/CJFDTOTAL-TKGC200205003.htm XU Hong-fa, WU Hua-jie, GUO Shao-ping, et al. Study on the parameters of pile soil contact surface element[J]. Prospecting Engineering (Rock and Soil Drilling Engineering), 2002(5): 10-12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TKGC200205003.htm
[25]	魏新江, 周洋, 魏纲. 土压平衡盾构掘进参数关系及其对地层位移影响的试验研究[J]. 岩土力学, 2013, 34(1): 73-79. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201301010.htm WEI Xin-jiang, ZHOU Yang, WEI Gang. Research of EPB shield tunneling parameter relations and their influence on stratum displacement[J]. Rock and Soil Mechanics, 2013, 34(1): 73-79. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201301010.htm

施引文献(31)

期刊类型引用(19)

1.	王利波. 穿越粉质黏土与粉砂混合地层盾构姿态控制优化研究. 江西建材. 2025(01): 263-265+269 . 百度学术
2.	李崇学. 软土地层工况下隧道盾构施工技术研究. 建筑机械. 2024(01): 84-88 . 百度学术
3.	王刚，张津钰，吕杨. 双线盾构隧道下穿铁路路基施工过程数值模拟. 施工技术(中英文). 2024(03): 42-48 . 百度学术
4.	王刚，张津钰，吕杨. 软土场地双线盾构地铁隧道施工数值模拟分析. 施工技术(中英文). 2024(03): 35-41 . 百度学术
5.	赵云，王超伟，陈樟龙，张卫民，凌道盛，肖昭然. 非饱和半空间受埋置集中力作用初值解. 土木工程学报. 2024(05): 76-85 . 百度学术
6.	李远帆，王媛，任杰，董琪，陈龙，王志奎. 泥水盾构隧道地层渗透压力的确定及规律研究. 人民黄河. 2024(05): 138-144 . 百度学术
7.	蔡晓明，潘泓，骆冠勇，曹洪. 大直径盾构施工引起的软土竖向变形计算研究. 河南理工大学学报(自然科学版). 2023(01): 185-193 . 百度学术
8.	王烨晟，吴勇，赵良云，李伟，姜宜杰，赵焕，丁智. 城市地下工程盾构施工风险分级管控平台研发与应用分析. 现代隧道技术. 2023(01): 76-89+106 . 百度学术
9.	袁侨蔚，刘远明，黄城，欧洵. 上软下硬地层盾壳摩擦对地表变形的影响. 中国水运(下半月). 2023(03): 92-93 . 百度学术
10.	彭书琪，王亮. 航道疏浚工程施工中疏浚船舶组合应用. 中国水运. 2023(06): 93-94 . 百度学术
11.	丁智，冯丛烈，董毓庆，徐涛，张默爆. 先行、后行盾构不同位置施工对土体变形影响研究. 铁道学报. 2022(03): 158-170 . 百度学术
12.	孙阳，刘蒙蒙，宋德威，徐振扬，余杰. 半封闭地下空间中盾构掘进对土体的扰动分析. 三峡大学学报(自然科学版). 2022(03): 55-61 . 百度学术
13.	刘玉辉，武保华，贾宾. 养护条件对预制盾构管片混凝土力学性能及微观形貌的影响. 中国港湾建设. 2022(04): 34-38 . 百度学术
14.	李婷，姜谙男，张峰瑞，钟越，徐波. 节理岩体对盾构开挖稳定性和地层损失率的影响. 工业建筑. 2022(03): 29-37 . 百度学术
15.	李平，鹿庆蕊，李栋伟，高金贺，张敏思. 软土地区盾构隧道施工稳定性研究. 公路工程. 2022(04): 70-77+110 . 百度学术
16.	周洁. 大直径泥水盾构机滚动角纠偏技术. 安徽建筑. 2021(01): 164-166 . 百度学术
17.	胡指南，孟祥飞，刘志春，林攀，王煦霖. 双线盾构扩建地铁车站的插管冻结法及施工力学特性研究. 隧道建设(中英文). 2021(04): 579-587 . 百度学术
18.	丁智，董毓庆，张霄，马少俊. 盾构姿态变化对管片影响与控制研究及展望. 科学技术与工程. 2021(21): 8745-8756 . 百度学术
19.	刘磊. 软弱土地层下双线隧道盾构施工引起的地表沉降及其敏感性分析. 建筑结构. 2021(S2): 1707-1712 . 百度学术