地铁车站结构端部效应影响范围研究

王国波; 郝朋飞; 孙富学

doi:10.11779/CJGE202008008

地铁车站结构端部效应影响范围研究 English Version

王国波^{1, 2,},
郝朋飞¹,
孙富学^2, ,

1.
武汉理工大学道路桥梁与结构工程湖北省重点实验室,湖北　武汉　430070
2.
温州大学建筑工程学院,浙江　温州　325000

基金项目:

国家自然科学基金项目 51878529

国家自然科学基金项目 51678465

武汉理工大学研究生优秀学位论文培育项目 2018-YS-044

详细信息

作者简介:
王国波(1979—),男,博士,教授,主要从事工程结构抗震分析方面的研究和教学工作。E-mail：wgb16790604@126.com

通讯作者:
孙富学, E-mail：sunfuxue@163.com

中图分类号: TU43
计量
- 文章访问数: 268
- HTML全文浏览量: 21
- PDF下载量: 155
出版历程
- 收稿日期: 2019-12-01
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-07-31

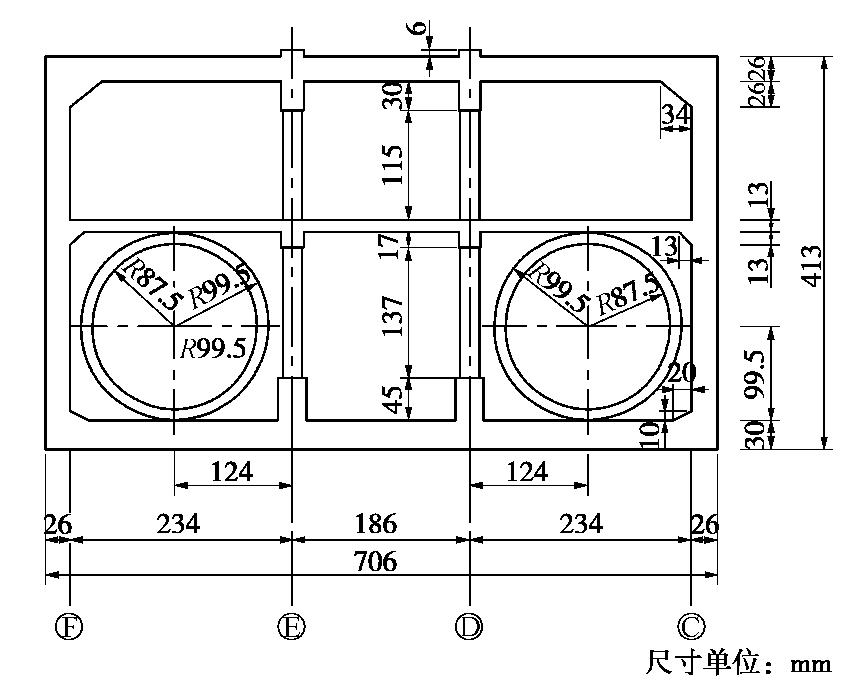
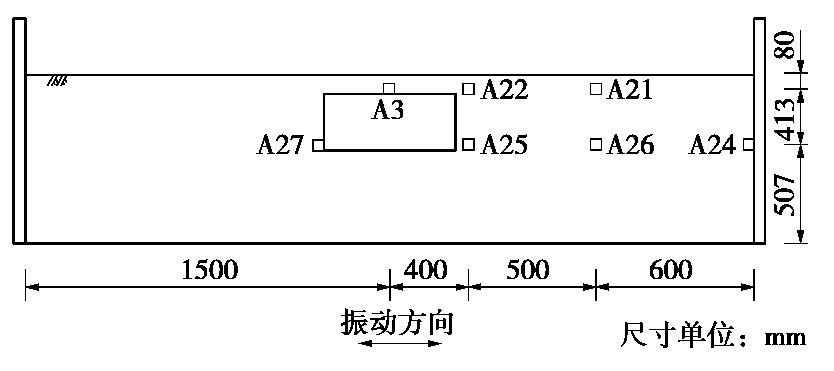
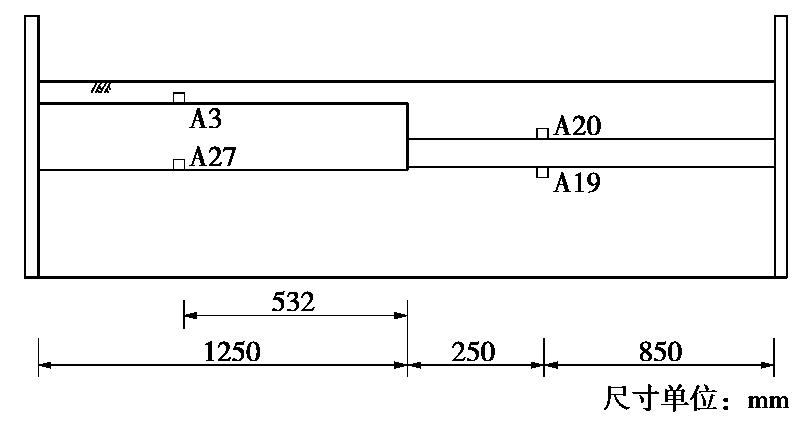
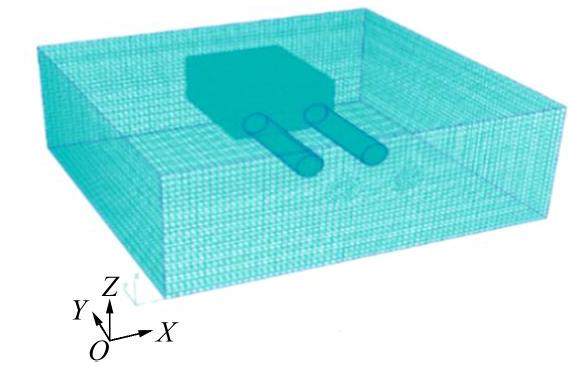
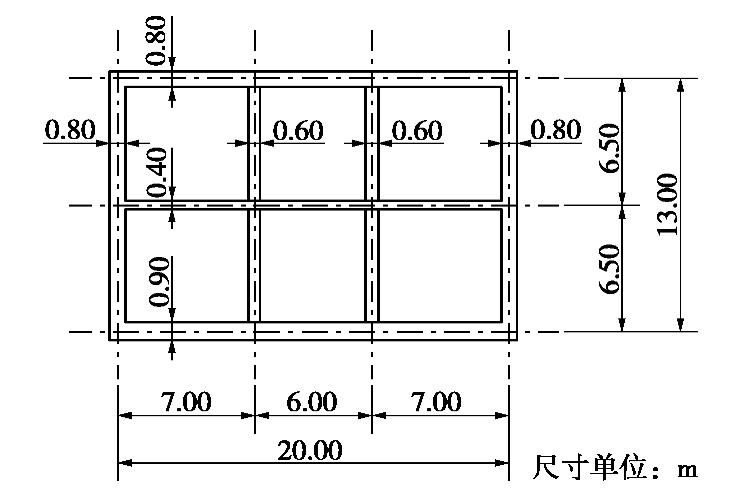
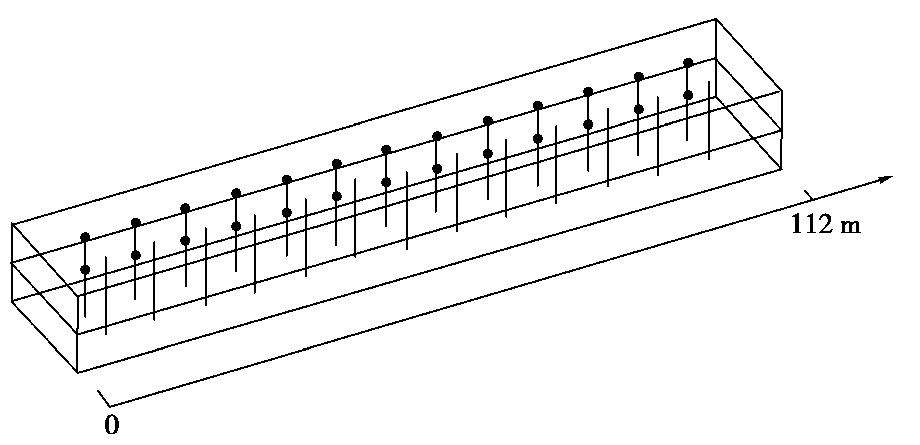
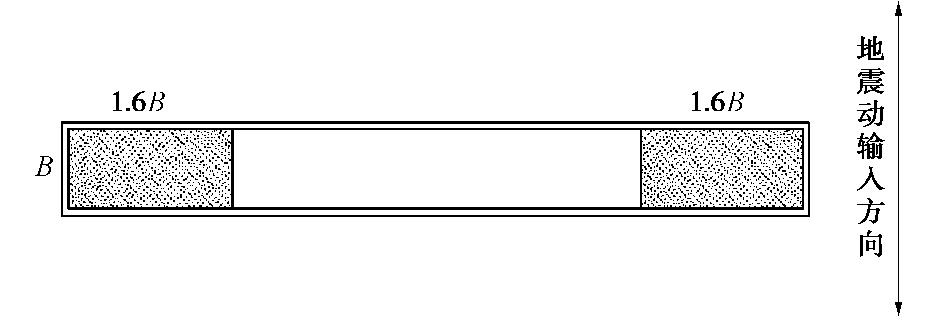
Spatial influence scope of end wall of metro station structures

1.
Hubei Key Laboratory of Roadway, Bridge & Structure Engineering, Wuhan University of Technology, Wuhan 430070, China
2.
College of Civil Engineering and Architecture, Wenzhou University, Wenzhou 325000, China

摘要

摘要: 常规的地铁车站抗震设计均是选择跨中截面按平面问题进行计算分析和设计,但在靠近车站前后端墙的区域必然受端墙及区间隧道的影响,从而应考虑其空间效应,即端墙的端部效应。基于对地铁车站及区间隧道振动台试验的数值模拟,验证数值模型的合理性,然后对地铁车站结构端部空间影响范围进行一系列的数值分析,主要考虑地铁车站结构跨数及层数、土体参数、地震波类型及幅值以及区间隧道数量的影响。计算分析结果表明：车站结构的跨数、层数以及区间隧道的数量均会对地铁车站端部影响范围产生一定的影响,车站结构端部影响范围最大的为2层3跨车站,其影响范围为1.6B（B为结构宽度）；地铁车站结构端部效应影响范围与其自身结构特性相关,而受土体参数和地震波类型及幅值影响较小,同时对比分析表明采用柱端弯矩作为端部影响范围的评价指标更为合理。
- 地铁车站 /
- 区间隧道 /
- 端部效应 /
- 地震响应
Abstract: The conventional seismic design of metro stations is to select the mid-span section for calculation analysis and design based on plane problem. However, the spatial effect of end walls must be considered because the area close to the front and rear end walls will inevitably be affected by the end walls and running tunnels. This effect is also called the end wall effect. The rationality of the numerical model is verified based on the numerical simulation of shaking table tests on metro stations and running tunnels firstly. Then a series of parameter analysis is performed on the spatial influence scope of the end wall of the metro station structures, which mainly includes the influences of the number of spans and layers of the metro station structures, soil parameters, seismic wave types and amplitudes, and the number of running tunnels. The calculation and analysis results show that the number of spans, the number of layers and the number of tunnels of the station structures will have certain effect on end walls influence scope. The largest influence area of end wall is the station with 2 layers and 3 spans, and the influence range is 1.6B (B is the structure width). The influence range of end wall effect is related to their own structural characteristics, but they are less affected by the soil parameters and seismic wave types and amplitudes. At the same time, the comparative analysis shows that it is more reasonable to use column end bending moment as evaluation indexes for end wall influence range analysis.
- metro station /
- running tunnel /
- end wall effect /
- seismic response

HTML全文

0. 引言

近年来,由于地下水、盐的迁移和全球气温升高等物理现象改变了土体的蠕变机理。使土体在地基处理、水利工程和道路桥梁工程中会出现不稳定的非均匀沉降,从而对工程建设和使用防护产生了一系列的影响^[1-3]。

目前,对不含盐土体蠕变模型的研究已经较为成熟。现有的理论模型主要以经验模型、元件模型和弹黏塑性模型为主,并且三者都能够很好地描述在指定条件下土体的蠕变行为^[4-6]。其中,Yin等^[7-9]在等时间线和弹-黏塑性理论为基础建立了一维蠕变模型,该模型的本构理论简单,参数少并容易获得。此外还将其推广到一维应力松弛及三维应力状态下的蠕变和应力松弛。但是该模型不能描述盐渍土中土颗粒与孔隙溶液间离子相互作用关系及对蠕变效应的影响。

盐渍土是土中含有可溶性盐类,且盐分浓度较高的一类特殊土。而有关盐渍土固结蠕变的试验研究主要集中在氯盐渍土中。从采用完全侧限条件下的固结蠕变试验到三轴条件下的等压蠕变、剪切蠕变和应变率试验,并在此基础上采用盐溶液饱和后的冻结砂、黏土等岩土材料展开了一系列的研究讨论^[10-14]。在与盐渍土相关的本构理论研究中,学者们提出了能够描述饱和状态下孔隙溶液与土颗粒相互作用的概念模型和分形模型。并以渗透吸力为媒介桥梁,作为描述盐渍土中化学力学耦合的重要指标。Barbour等^[15]认为在盐溶液饱和后的土体中,由于土体的渗透性导致有效应力的增加,并且提出将有效应力和渗透吸力作为应力状态变量来描述土体的力学性质。Shivananda^[16]、Rao等^[17]分别讨论了外来盐对孔隙溶液渗透吸力的影响和Van't Hoff方程在有无Van't Hoff因子时计算值与试验值的误差范围。并且明确了在恒定荷载作用下,采用氯化钠和蒸馏水饱和后试样的应变差可以通过渗透吸力的增加来预测试样的渗透诱导固结。Xu等^[18]在上述理论的基础上采用分形理论描述了Van't Hoff方程中的渗透系数,提出了一种新的有效应力计算方法。

通过渗透吸力来描述岩土材料中化学-力学耦合性质已经成为研究盐渍土本构的一种有效研究方法。但是现有的理论主要是通过浓液的溶度来反映土水体系的化学性质,无法实现孔隙溶液中化学离子的定量描述,并且相关研究也主要集中在饱和氯盐中。因此本文对分别采用蒸馏水、氯化钠溶液和硫酸钠溶液饱和后的试样进行了固结蠕变试验,讨论了硫酸盐渍土与氯盐渍土的固结蠕变特性。在Van't Hoff方程中引入Pitzer离子相互作用模型,实现了土颗粒与孔隙溶液间的离子相互作用描述。在Yin-Graham一维蠕变模型的框架下建立了饱和盐渍土的一维蠕变模型,并结合蠕变试验结果,对原有模型和改进模型进行了详细的对比分析。

1. 试验条件与结果

1.1 试样制作

试验用土取自兰州七里河区。邴慧等^[19]研究表明,洗盐对土颗粒粒组和土体结构影响较为明显。因此表1给出了洗盐后土样的物理性质指标。

表 1 洗盐后土样的物理性质指标

Table 1. Physical properties of soil samples after salt washing

初始孔隙比e₀	颗粒相对密度	液限 $w_{L}$ /%	塑限 $w_{P}$ /%	塑限指数 $I_{P}$	土粒粒组含量/%
初始孔隙比e₀	颗粒相对密度	液限 $w_{L}$ /%	塑限 $w_{P}$ /%	塑限指数 $I_{P}$	$d$ ≤ $0 .005 mm$	$0 .005 mm< d <0 .075 mm$	$d$ ≥ $0 .075 mm$
0.66	2.7	28.2	18.4	9.8	20.33	71.11	8.56

下载: 导出CSV

| 显示表格

试验在杠杆式中压固结仪上进行,数据采集通过电子位移计和数据采集仪共同工作,不仅保证了采集数据的精度,也保证了数据采集的连续性。土样制做的主要步骤为：洗盐（蒸馏水）—风干—碾碎过筛（0.5 mm）—配水制样（无盐试样）—风干,主要步骤严格按照《土工试验方法标准》的要求。试样尺寸的大小为：直径6.18 cm,高度2 cm；制样含水率为16.88%,干密度为1.641 g/cm³。

试样饱和时先将干燥土样安放完成,然后向固结仪水槽中注一定浓度的盐溶液后立即加载。饱和溶液根据是否含盐与易溶盐种类分为蒸馏水、硫酸钠溶液和氯化钠溶液；其中硫酸钠和氯化钠溶液的浓度分设了3组,其质量摩尔浓度分别为0.6,1.2,1.8 mol/kg。其次硫酸盐渍土对应上述质量摩尔浓度的质量分数分别为7.6%,14.6%,20.4%,氯盐渍土对应上述质量摩尔浓度的质量分数分别为3.4%,6.6%,9.5%。在试验过程中为了保持溶液浓度、试验温度（ $25 ℃ \pm 1 ℃$ ）和饱和程度不变,在试验过程中设置了防止溶剂蒸发和保温隔热装置,并且在加载周期内保证水槽水位基本不变。

1.2 试验结果

（1）固结试验

固结回弹试验结合土样的物理特性将加荷卸荷顺序设计为50,100,200,300,400,800,1600,800,400,300,200 kPa,每级荷载持续时间为24 h。图1给出了采用不同溶液饱和下的固结试验结果。从图1中发现非盐渍土与盐渍土的固结曲线存在明显的差异,而且采用硫酸钠和氯化钠溶液饱和后的盐渍土固结曲线也有所不同。通过观察图1发现,易溶盐对压缩变形的影响是贯穿于整个固结回弹过程中的。从而导致了在不同固结应力下,相同浓度的同类盐渍土对压缩变形的贡献是基本相等的。这与图1所表现出在50～1600 kPa的固结曲线和1600～200 kPa的回弹曲线几乎平行的结果相符合。这也证实了孔隙溶液的变化不会改变土体的压缩系数、压缩指数与回弹再压缩指数^[13-14]。

图 1 不同盐溶液饱和下的固结试验结果

Figure 1. Consolidation test results under saturation of different salt solutions

下载: 全尺寸图片幻灯片

（2）蠕变试验

蠕变是土体的超静孔隙水压力消散后,有效应力不变的情况下土体继续被压缩的宏观表象。也可以认为是在排水固结过程中发生的次固结压缩。图2描述了土样分别在蒸馏水、硫酸钠和氯化钠溶液饱和下的恒载蠕变情况。其中图2（a）～（c）分别是在200,400,800 kPa作用下的蠕变过程,直观地反映了盐渍土与非盐渍土蠕变行为的差异。

图 2 不同孔隙溶液饱和下的蠕变试验结果

Figure 2. Creep test results under saturation of different pore solutions

下载: 全尺寸图片幻灯片

对比同一荷载情况下3种孔隙溶液饱和后的蠕变情况,发现孔隙溶液中盐分的存在增大了土体的初始蠕变变形与最终蠕变量。而这种增大的程度与含盐种类和含盐量息息相关。其次,盐渍土与非盐渍土的蠕变稳定时间明显不同,但是不同种类盐渍土的蠕变稳定时间在试验中没有表现出较为明显的差异。当荷载为200 kPa时,蒸馏水饱和下的蠕变时间大约在4.8 d,而由盐溶液饱和后的蠕变时间为6 d左右。表明土体盐渍化后的蠕变性明显要强于非盐渍化。同时还发现在盐溶液浓度为1.8 mol/kg时,经硫酸钠和氯化钠溶液饱和后的试验结果恰好与0.6和1.2 mol/kg的结果相反,同时在400,800 kPa和固结试验中也表现出了类似的结果。造成这种现象的原因可能是当浓度超过1.2 mol/kg时,由于硫酸钠溶液的活度小于氯化钠溶液,从而导致氯盐渍土表现出稍强的固结蠕变特性。

对比同盐类和盐度的盐渍土在不同荷载下的蠕变结果发现：随着荷载的增大,蠕变变形越大,并且蠕变稳定所需要的时间越长。当浓度为1.2 mol/kg时荷载为200,800 kPa下的蠕变稳定时间分别为5.8,6.1 d。

2. 饱和盐渍土的一维蠕变模型

2.1 渗透吸力

土中的吸力由基质吸力和渗透吸力（溶质吸力）组成,而在饱和土中一般认为总吸力等于渗透吸力。渗透吸力是由于孔隙水中溶解盐的存在导致土体中孔隙水化学势的降低,其实质是通过土体内外的渗透压,使土体内部出现负的孔隙水压力,从而导致有效应力的增加（图3）。

图 3 饱和盐渍土中渗透吸力示意图

Figure 3. Schematic diagram of osmotic suction in saturated saline soils

下载: 全尺寸图片幻灯片

渗透吸力可由Van't Hoff方程^{[18, 21]}给出：

$π = ν R T c ϕ$ ,

(1)

式中, $R$ 为通用的摩尔气体常数, $R = 8 .32$ $J/mol \cdot k$ , $T$ 为绝对K氏温度（T=298.15K）, $c$ 为孔隙溶液的浓度（ $mol/L$ ）, $ϕ$ 为溶质渗透系数,可根据Pitzer^[22-23]提出的电解质渗透系数公式计算。当孔隙溶液只有一种溶质（MX）时：

$ϕ = 1+ | z_{M} z_{X} | f_{ϕ} + 2 m \frac{v_{M} v_{X}}{v} B_{ϕ}^{MX} + 2 m^{2} \frac{{(v_{M} v_{X})}^{3 / 2}}{v} C_{ϕ}^{MX}$ ,

(2)

式中, $z_{M}, z_{X}$ 分别为电解质阳离子M和阴离子X的电荷数； $v$ 为盐溶解后的总离子数, $v_{M}$ 为阳离子的离子总数, $v_{X}$ 为阴离子的离子总数,即 $v = v_{M} + v_{X}$ ； $m$ 为盐溶液的质量摩尔浓度； $f_{ϕ}$ 为Debye-Hückel项； $B_{ϕ}^{MX}$ 和 $C_{ϕ}^{MX}$ 是离子相互作用系数。

表2给出温度在298.15K时,采用式（1）计算氯盐渍土和硫酸盐渍土在不同浓度时的渗透吸力大小。将其与Van't Hoff方程计算结果和Fredlund等^[24]采用滤纸法测试结果进行了比较。说明该公式不仅明确了土粒与孔隙溶液间化学-力学耦合效应的离子作用,而且有效地改善了使用Van't Hoff方程计算时随浓度增大而产生的较大误差。

表 2 298.15K时不同浓度氯化钠和硫酸钠溶液的渗透吸力

Table 2. Osmotic suctions of sodium chloride and sodium sulfate solutions with different concentrations at 298.15K (kPa)

浓度/(mol·L^-1)	$NaCl$	Na₂SO₄
0.2	915.11	1119.33
0.5	2281.01	2597.24
0.6	2742.22	3067.43
1.2	5593.46	5787.71
1.6	7584.01	7559.54
1.7	8093.60	8000.32
1.8	8608.10	8440.47
2.0	9651.91	9310.95

下载: 导出CSV

| 显示表格

2.2 蠕变方程

土体的固结蠕变由可恢复的瞬时变形和不可恢复的延时变形组成。其中瞬时变形是完全弹性的,延时变形是黏性变形和塑性变形的总和,并且黏性变形和塑性变形是同时发生的。因此,基于上述假设,Yin等^[7-8]给出了非盐渍土的一维蠕变方程：

$ε_{z} = ε_{z 0}^{ep} + \frac{λ}{V_{0}} \ln (\frac{σ_{z}^{*}}{σ_{z 0}^{*}}) + \frac{ξ}{V_{0}} \ln (\frac{t}{t_{0}})$ 。

(3)

式中 $σ_{z}^{*}$ 为有效应力； $ε_{z 0}^{ep}$ 为黏性应变为零时的弹塑性应变,即 $σ_{z}^{*} = σ_{z 0}^{*}$ 时对应的应变； $V_{0}$ 为土体的初始比体积, $V_{0} = 1 + e_{0}$ ； $λ / V_{0}$ 为参考时间线的斜率； $ξ / V_{0}$ 为蠕变曲线在 $ε_{z} - \ln t$ 中直线段的斜率； $t = t_{0} + t_{e}$ , $t_{0}$ , $t_{e}$ 分别为参考时间和等效时间。

饱和盐渍土在轴向荷载作用下的应力状态变量可以理解为由传统的有效应力和颗粒孔隙间的净排斥力组成,且两部分应力可以看成一个应力状态变量。其中可以通过渗透压将颗粒间的排斥应力变化与流体间的渗透吸力联系起来,满足了渗透吸力作为应力状态变量的一致性条件^[15-18]。因此饱和盐渍土的总有效应力由传统有效应力和有效渗透应力组成,即

$σ^{*} = σ_{z}^{*} + σ_{π}^{*}$ 。

(4)

式中 $σ_{z}^{*}$ 为传统的有效应力,其值由Terzaghi提出的饱和土的有效应力原理计算,即 $σ_{z}^{*} = σ_{z} - u_{w}$ ； $σ_{π}^{*}$ 为有效渗透应力, $σ_{π}^{*} = χ π$ , $χ$ 是量纲为“1”的参数,且 $0 < χ < 1$ 。

将式（4）代入式（3）可得到改进的饱和盐渍土一维蠕变模型：

$ε_{z} = ε_{0}^{ep} + \frac{λ}{V_{0}} \ln (\frac{σ^{*}}{σ_{0}^{*}}) + \frac{ξ}{V_{0}} \ln \frac{t}{t_{0}}$ 。

(5)

3. 模型参数

本文是在Yin-Graham模型的框架上考虑了盐渍土中孔隙盐溶液的有效渗透应力对固结蠕变的贡献；因此模型参数包含了原有的Yin-Graham模型参数外（ $σ_{0}^{*}$ , $ε_{0}^{ep}$ , $λ / V_{0}$ , $ξ / V_{0}$ , $t_{0}$ ）,还新增了描述渗透应力的参数（ $χ$ , $f_{ϕ}$ , $B_{ϕ}^{M X}$ , $C_{ϕ}^{M X}$ ）。

3.1 Yin-Graham模型参数

基本参数 $σ_{0}^{*}$ , $ε_{0}^{ep}$ 和 $λ / V_{0}$ 可以通过24 h固结试验测得,其中 $λ = Δ e / [\ln (σ^{*} / σ_{0}^{*})]$ ,由试验结果得到 $λ$ 的值不随孔隙溶液改变。图4分别给出了 $σ_{0}^{*}$ 和 $λ$ 的取值方法,其中根据图1的试验结果和 $σ_{0}^{*}$ 的取值方法发现 $σ_{0}^{*}$ 受土中含盐种类和含盐量的影响显著,故不同溶液饱和下的 $σ_{0}^{*}$ 也不尽相同,而 $ε_{0}^{ep}$ 为 $σ^{*} = σ_{0}^{*}$ 时的应变。 $t_{0}$ 为参考时间,取 $t_{0} = 10 min$ 。

图 4 参数示意图

Figure 4. Schematic diagram of parameters

下载: 全尺寸图片幻灯片

盐渍土的蠕变系数 $ξ / V_{0}$ 不是一个定值,它会随着荷载和含盐量的变化而改变。表3给出了400 kPa和800 kPa作用下的计算结果,结果显示蠕变系数与压缩指数、回弹指数不同,它会随着荷载和渗透吸力的增大而增大。

表 3 模型参数

Table 3. Model parameters

孔隙溶液	浓度m/(mol·kg^-1)	$σ_{0}^{*}$ /kPa	蠕变系数 $ξ / V$		$C_{ϕ}^{MX}$ /( ${kg}^{2} \cdot {mol}^{- 2}$ )	$f_{ϕ}$ / ${(kg \cdot mol)}^{\frac{1}{2}}$	$B_{ϕ}^{MX}$ /( $kg \cdot {mol}^{- 1}$ )
孔隙溶液	浓度m/(mol·kg^-1)	$σ_{0}^{*}$ /kPa	400 kPa	800 kPa	$C_{ϕ}^{MX}$ /( ${kg}^{2} \cdot {mol}^{- 2}$ )	$f_{ϕ}$ / ${(kg \cdot mol)}^{\frac{1}{2}}$	$B_{ϕ}^{MX}$ /( $kg \cdot {mol}^{- 1}$ )
蒸馏水	0	79	0.03053	0.03284	0	0	0
氯化钠	0.6	77.12	0.03146	0.03634	0.00106	-0.1572	0.1307
	1.2	71.05	0.03494	0.03730		-0.1853	0.1054
	1.8	61.21	0.03626	0.03859		-0.2012	0.0944
硫酸钠	0.6	75.09	0.03306	0.03655	-0.00483	-0.2012	0.1098
	1.2	69.26	0.03466	0.03710		-0.2267	0.0670
	1.8	64.40	0.03552	0.03827		-0.2401	0.0550

下载: 导出CSV

| 显示表格

3.2 有效渗透应力参数

有效渗透应力是渗透吸力的宏观表达,而渗透吸力又通过渗透系数和溶液浓度描述盐渍土的化学物理性质。因此参数包含了模型参数 $χ$ 和离子相互作用参数（ $f_{ϕ}$ , $B_{ϕ}^{MX}$ , $C_{ϕ}^{MX}$ ）。并且都是在恒定的体积、温度和化学状态下的拟合参数与试验参数。其中 $f_{ϕ}$ 和 $B_{ϕ}^{MX}$ 采用下式计算^[22]：

$f_{ϕ} = - A_{ϕ} \frac{I^{1 / 2}}{1 + θ I^{1 / 2}}, I = (1/2) \sum m_{i} z_{i}^{2},$

(6)

$B_{ϕ}^{MX} = D_{0}^{MX} + D_{1}^{MX} \exp (α_{1} I^{1 / 2}) + D_{2}^{MX} \exp (α_{2} I^{1 / 2})$ 。

(7)

式中 $A_{ϕ}$ 为Debye-Hückel参数,当温度等于25℃时, $A_{ϕ} = 0 {.392 kg}^{- 1 / 2} \cdot {mol}^{- 1 / 2}$ ； $I$ 为离子强度； $θ$ 为恒定常数, $θ = 1 .2 {kg}^{1 / 2} / {mol}^{1 / 2}$ ； $m_{i}$ 为离子 $i$ 的质量摩尔浓度, $m_{i} = v_{i} m$ ； $B_{ϕ}^{MX}$ 的数值是由离子强度 $I$ 所决定的,当电解质为一价型时 $B_{ϕ}^{MX}$ 值取前两项；此时 $α_{1} = 2$ ； $D_{0}^{MX}$ , $D_{1}^{MX}$ , $D_{2}^{MX}$ 是盐溶液中溶质阴阳离子决定的相互作用参数^[25]。

$χ$ 是表征渗透吸力转化为有效渗透应力的效率参数。当 $χ = 1$ 时,表示盐渍土的渗透吸力完全转化为有效渗透应力,即所有的溶液离子都与土颗粒发生反应。而 $χ = 0$ 时,表明盐渍土中的易溶盐离子都没有与土粒相互反应。显然这两种极限状态是不存在的,因此认为 $χ \in (0, 1)$ 。图5是在相同条件下参数 $χ$ 的不同取值情况,发现参数 $χ$ 的敏感性在计算蠕变变形时表现的不强,而本文通过模型计算与试验结果拟合分析,确定 $χ =0 .15$ 。

图 5 参数的敏感性分析

Figure 5. Sensitivity analysis of parameters

下载: 全尺寸图片幻灯片

4. 模型验证

通过改进模型和Yin-Graham模型对饱和盐渍土和非盐渍土恒载蠕变结果进行对比分析。验证了改进模型对预测饱和盐渍土一维蠕变行为的有效性。

图6为400,800 kPa下饱和非盐渍土的蠕变试验结果与Yin-Graham蠕变方程式（3）计算结果的对比情况。根据图示结果发现,采用Yin-Graham一维蠕变模型能够很好地预测饱和非盐渍土的蠕变行为。

图 6 蒸馏水饱和下的蠕变试验结果与Yin-Graham模型计算结果

Figure 6. Creep test results of saturated distilled water and calculated results of Yin-Graham model curves

下载: 全尺寸图片幻灯片

图7,8为分别采用硫酸钠溶液和氯化钠溶液饱和后的恒载蠕变试验结果及使用方程式（3）,（5）计算结果的对比情况。从图中可以发现采用Yin-Graham蠕变方程式（3）无法准确预测饱和盐渍土的蠕变行为,总是小于试验结果。采用改进模型式（5）不仅能够在其数值上预测饱和盐渍土的蠕变效应,而且还能够在详细描述饱和盐渍土化学力学耦合效应的同时预测不同类饱和盐渍土的蠕变特性。

图 7 硫酸钠溶液饱和下的蠕变试验与模型计算结果

Figure 7. Creep tests and model results under saturation of sodium sulfate solution

下载: 全尺寸图片幻灯片

图 8 氯化钠溶液饱和下的蠕变试验与模型计算结果

Figure 8. Creep tests and model results under saturation of sodium chloride solution

下载: 全尺寸图片幻灯片

图7是饱和硫酸盐渍土的蠕变结果。对比分析了相同轴向荷载作用下和同浓度溶液饱和下的模拟结果。发现Yin-Graham模型在孔隙溶液较低时,其计算结果与试验结果很接近,而且随着轴向荷载的增加计算误差也有所减小。从总体上讲,计算误差的大小同盐渍土孔隙溶液浓度呈正比,而与轴向荷载成反比。图8是饱和氯盐渍土的模拟结果,表现出与硫酸钠盐渍土相同的规律。所以在低浓度高承载作用时,饱和盐渍土的蠕变应变量可以采用Yin-Graham模型预测。但是在较高浓度的饱和盐渍土中,Yin-Graham模型的适用性有所降低。此类现象正好同图1,2固结蠕变试验结果和表3渗透理论的结果相一致。

5. 结论

首先通过固结蠕变试验,分析了盐渍土与非盐渍土、硫酸盐渍土与氯盐渍土的固结蠕变特性。然后基于Pitzer离子相互作用模型和Van't Hoff方程,完善了饱和盐渍土中化学力学耦合效应的描述。并在Yin-Graham模型的基础上,建立了饱和盐渍土的蠕变模型。此外还将模型与试验结果进行了比较,得到以下3点结论。

（1）相同的土粒粒组、荷载和温度条件下,盐渍土较非盐渍土表现出更强的蠕变性；而硫酸盐渍土与氯盐渍土也表现出不同的固结蠕变效应,并且在高、低浓度时的固结蠕变行为表现出相反的结果。

（2）改进的Van't Hoff方程不仅能够更深层次地反映饱和盐渍土中易溶盐的离子化学性质,也降低了使用传统Van't Hoff方程的计算误差；为建立盐渍土本构模型提供了帮助。

（3）改进后的Yin-Graham一维蠕变模型,不仅能够描述饱和盐渍土中物理化学相互作用,而且可以更加有效地反应其蠕变行为。

图 1 地铁车站接头结构模型

Figure 1. Structural model for joints in subway stations

下载: 全尺寸图片幻灯片

图 2 地铁车站接头结构剖面图

Figure 2. Cross-section view of joints of subway station

下载: 全尺寸图片幻灯片

图 3 加速度传感器布置图（③轴剖面）

Figure 3. Arrangement of acceleration sensors (③ axial section)

下载: 全尺寸图片幻灯片

图 4 加速度传感器布置（垂直振动方向）

Figure 4. Arrangement of acceleration sensors (vertical vibration direction)

下载: 全尺寸图片幻灯片

图 5 有限元模型示意图

Figure 5. Schematic diagram of finite element model

下载: 全尺寸图片幻灯片

图 6 振动台台面实测波加速度时程及频谱曲线

Figure 6. Time-history and spectral curves of measured wave acceleration on shaking table

下载: 全尺寸图片幻灯片

图 7 0.11g上海人工波工况下测点加速度时程与频谱曲线的试验与模拟结果对比

Figure 7. Comparison between experimental and simulated results of acceleration time-history and spectral curves at measured points under 0.11g Shanghai artificial wave

下载: 全尺寸图片幻灯片

图 8 0.11gEl-Centro工况下测点加速度时程与频谱曲线的试验与模拟结果对比

Figure 8. Comparison between experimental and simulated results of acceleration time-history and spectral curves at measured points under 0.11g El-Centro conditions

下载: 全尺寸图片幻灯片

图 9 0.51gEl-Centro工况下测点加速度时程与频谱曲线的试验与模拟结果对比

Figure 9. Comparison between experimental and simulated results of acceleration time-history and spectral curves at measured points under 0.51gEl-Centro conditions

下载: 全尺寸图片幻灯片

图 10 标准工况2层3跨地铁车站截面图

Figure 10. Cross-sectional view of a subway station with 2 floors and 3 spans under standard conditions

下载: 全尺寸图片幻灯片

图 11 3层3跨–4孔区间隧道结构有限元模型图

Figure 11. Finite element model for a three-story, three-span and four-hole tunnel structure

下载: 全尺寸图片幻灯片

图 12 不同工况的地铁车站截面示意图（m）

Figure 12. Schematic cross-sections of subway stations under different working conditions（m）

下载: 全尺寸图片幻灯片

图 13 地震波时程及频谱图

Figure 13. Time histories and spectra of seismic waves

下载: 全尺寸图片幻灯片

图 14 2层3跨地铁车站测点布置图

Figure 14. Arrangement of measuring points of a metro station with 2 layers and 3 spans

下载: 全尺寸图片幻灯片

图 15 地铁车站参考柱柱顶加速度时程曲线

Figure 15. Time-history curve of top of reference column of subway station

下载: 全尺寸图片幻灯片

图 16 不同跨数的地铁车站结构地震响应以及其与参考点比值沿车站长度方向变化曲线

Figure 16. Seismic responses of a subway station structure with different spans and its ratio to reference point along length of the station

下载: 全尺寸图片幻灯片

图 17 不同层数的地铁车站结构地震响应以及其与参考点比值沿车站长度方向变化曲线

Figure 17. Seismic responses of a subway station structure with different layers and its ratio to reference point along length of station

下载: 全尺寸图片幻灯片

图 18 不同土层参数中的地铁车站结构地震响应以及其与参考点比值沿车站长度方向变化曲线

Figure 18. Curves of seismic response of subway station structure with different soil layer parameters and ratio to reference point along station

下载: 全尺寸图片幻灯片

图 19 不同地震波作用下地铁车站结构地震响应以及其与参考点比值沿车站长度方向变化曲线

Figure 19. Seismic responses of subway station structure under different seismic waves and its ratio to reference point along length of the station

下载: 全尺寸图片幻灯片

图 20 不同区间隧道数量的地铁车站结构地震响应以及其与参考点比值沿车站长度方向变化曲线

Figure 20. Seismic response of subway station structure with different number of tunnels and its ratio to the reference point along the length of the station

下载: 全尺寸图片幻灯片

图 21 地铁车站端部空间影响范围

Figure 21. Spatial influence scopes of end wall of subway station

下载: 全尺寸图片幻灯片

表 1 模型结构及模型土材料参数

Table 1 Material parameters of model structure and model soil

材料参数	密度/(kg·m^-3)	弹性模量/MPa	泊松比	剪切模量/MPa
模型土	1760	30.8	0.4	11
微粒混凝土	2100	9800	0.2	—

下载: 导出CSV

表 2 材料参数表

Table 2 Material parameters

材料	土层厚度/m	密度/(kg·m^-3)	弹性模量/MPa	泊松比	波速/(m·s^-1)	A	2B	γ_r
软土	60	1800	209	0.45	200	1	0.77	0.00123
硬土	60	1900	790	0.30	400	1	0.76	0.00074
基岩	10	2200	1320	0.20	500	1	0.68	0.00177
混凝土	—	2500	30000	0.20	—	—	—	—

下载: 导出CSV

表 3 计算工况表

Table 3 Calculation conditions

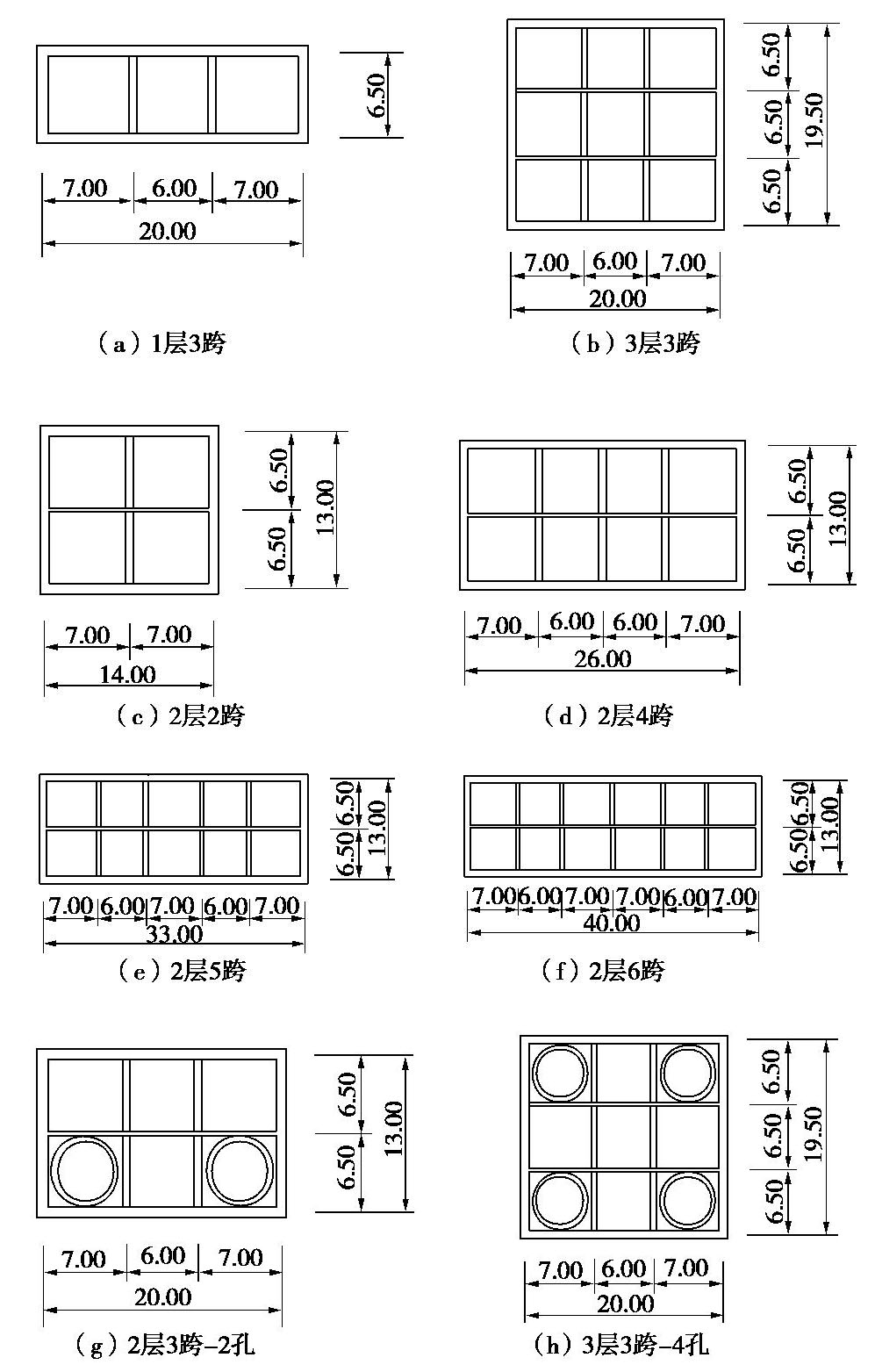
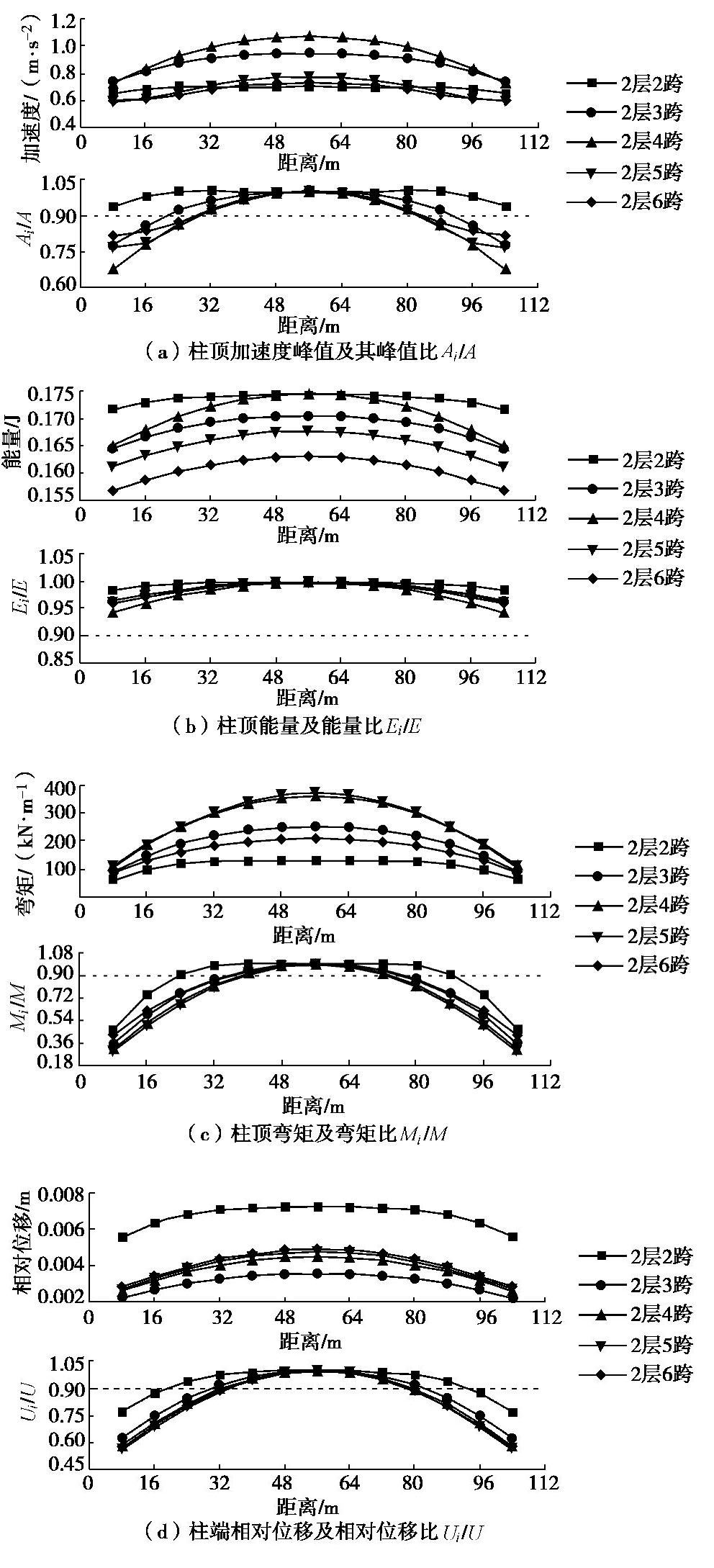
工况	车站结构	地震波	土体参数	区间隧道	备注
1	2层3跨	0.1g El-Centro波	软土	无区间隧道	标准工况
2	2层2跨	0.1g El-Centro波	软土	无区间隧道	车站跨数的影响
3	2层4跨
4	2层5跨
5	2层6跨
6	1层3跨	0.1g El-Centro波	软土	无区间隧道	车站层数的影响
7	3层3跨	0.1g El-Centro波	软土	无区间隧道	车站层数的影响
8	2层3跨	0.1g El-Centro波	硬土	无区间隧道	土性参数的影响
9	2层3跨	0.4g El-Centro波	软土	无区间隧道	地震波类型、幅值的影响
10	2层3跨	0.1g Kobe波	软土	无区间隧道	地震波类型、幅值的影响
11	2层3跨–2孔	0.1g El-Centro波	软土	2孔区间隧道	区间隧道的影响
12	3层3跨–4孔	0.1g El-Centro波	软土	4孔区间隧道	区间隧道的影响

下载: 导出CSV

表 4 不同跨数地铁车站端部影响范围

Table 4 Influence ranges of end wall of metro station with different spans

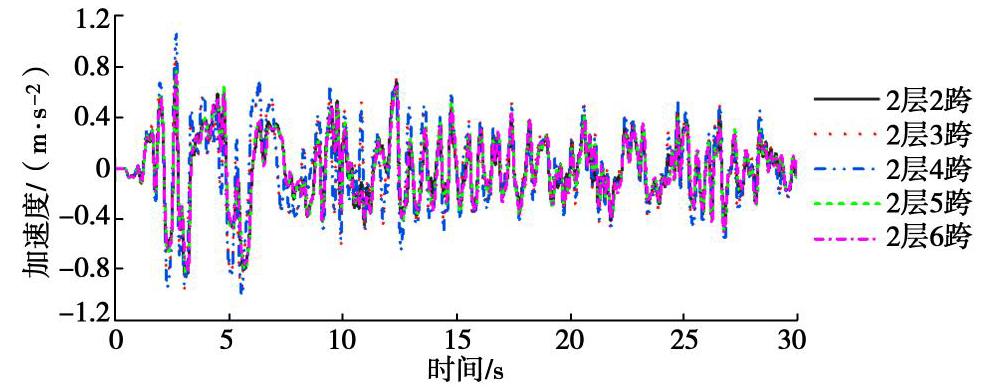
车站结构形式	车站宽度B/m	不同评价指标下的端部影响范围/m				最大影响范围
车站结构形式	车站宽度B/m	加速度	能量	弯矩	相对位移	最大影响范围
2层2跨	14	0	0	16	16	1.1B
2层3跨	20	16	0	32	24	1.6B
2层4跨	26	24	0	32	32	1.2B
2层5跨	32	24	0	32	32	1.0B
2层6跨	40	24	0	32	32	0.8B

下载: 导出CSV

表 5 不同层数地铁车站端部影响范围

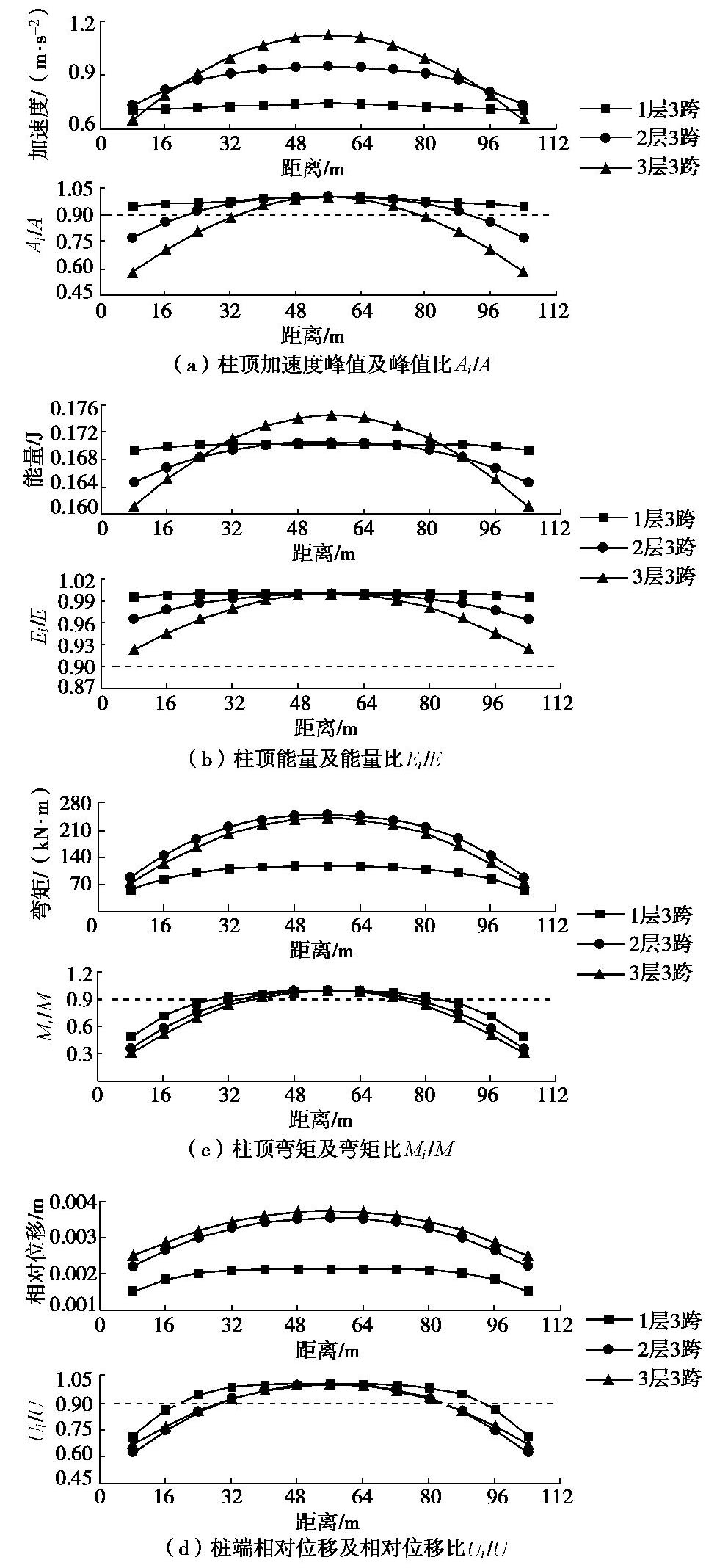
Table 5 Influence ranges of end wall of metro station with different layers

车站结构形式	车站宽度B/m	不同评价指标下的端部影响范围/m				最大影响范围
车站结构形式	车站宽度B/m	加速度	能量	弯矩	相对位移	最大影响范围
1层3跨	20	0	0	24	16	1.2B
2层3跨	20	16	0	32	24	1.6B
3层3跨	20	32	0	32	24	1.6B

下载: 导出CSV

表 6 不同土层参数中地铁车站端部影响范围

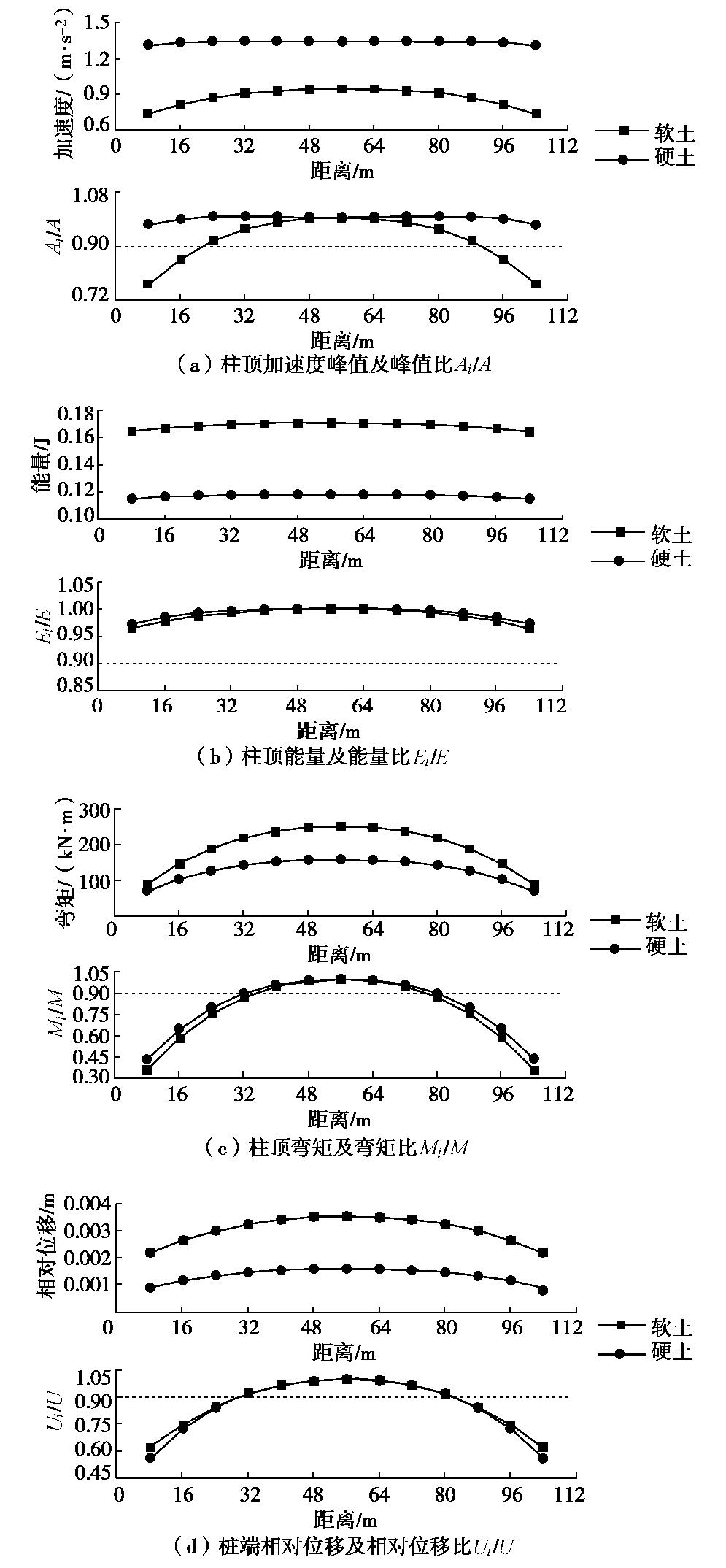
Table 6 Influence ranges of end wall of metro station with different soil layer parameters

土体参数	车站宽度B/m	不同评价指标下的端部影响范围/m				最大影响范围
土体参数	车站宽度B/m	加速度	能量	弯矩	相对位移	最大影响范围
软土	20	16	0	32	24	1.6B
硬土	20	0	0	32	24	1.6B

下载: 导出CSV

表 7 不同地震波作用下地铁车站端部影响范围

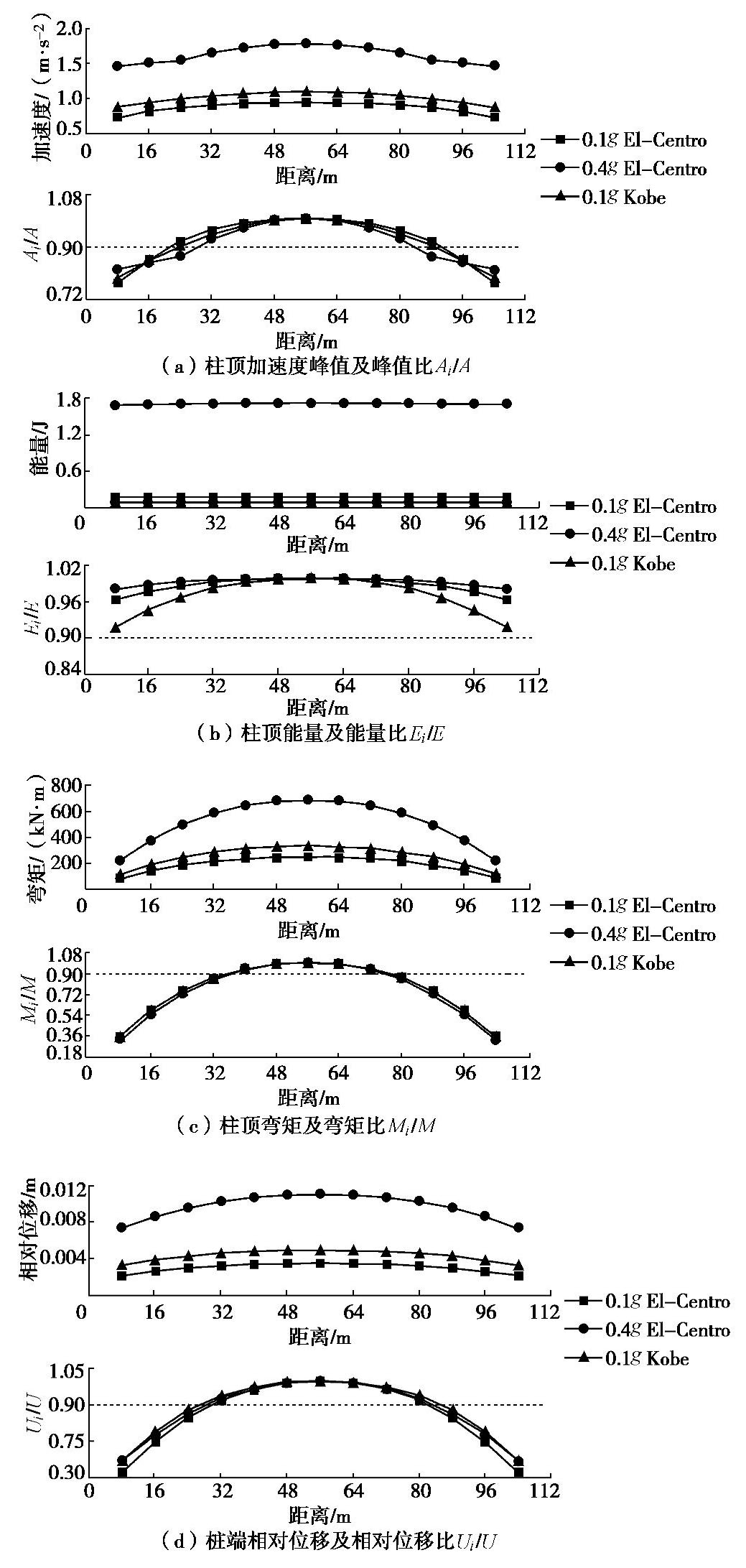
Table 7 Influence ranges of end wall of metro station under different seismic waves

地震波类型	车站宽度B/m	不同评价指标下的端部影响范围/m				最大影响范围
地震波类型	车站宽度B/m	加速度	能量	弯矩	相对位移	最大影响范围
0.1g El Centro	20	16	0	32	24	1.6B
0.4g El Centro	20	24	0	32	24	1.6B
0.1g Kobe	20	16	0	32	24	1.6B

下载: 导出CSV

表 8 不同区间隧道数量的地铁车站端部影响范围

Table 8 Influence ranges of end wall of metro station with different number of tunnels

车站结构形式	车站宽度B/m	不同评价指标下的端部影响范围/m				最大影响范围
车站结构形式	车站宽度B/m	加速度	能量	弯矩	相对位移	最大影响范围
2层3跨	20	16	0	32	24	1.6B
2层3跨–2孔	20	0	0	24	16	1.2B
3层3跨	20	32	0	32	24	1.6B
3层3跨–4孔	20	32	0	32	32	1.6B

下载: 导出CSV

参考文献(12)

[1]	ZLATANOVIĆ E, LUKIĆ D Č, PROLOVIĆ V, et al. Comparative study on earthquake-induced soil–tunnel structure interaction effects under good and poor soil conditions[J]. European Journal of Environmental and Civil Engineering, 2015, 19(8): 1000-1014. doi: 10.1080/19648189.2014.992548
[2]	庄海洋, 王修信, 陈国兴. 软土层埋深变化对地铁车站结构地震反应的影响规律研究[J]. 岩土工程学报, 2009, 31(8): 1258-1266. doi: 10.3321/j.issn:1000-4548.2009.08.017 ZHUANG Hai-yang, WANG Xiu-xin, CHEN Guo-xing. Earthquake responses of subway station with different depths of soft soil[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(8): 1258-1266. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.08.017
[3]	陈磊, 陈国兴, 毛昆明. 框架式地铁车站结构大地震近场地震反应特性的三维精细化非线性分析[J]. 岩土工程学报, 2012, 34(3): 490-496. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201203020.htm CHEN Lei, CHEN Guo-xing, MAO Kun-ming. 3D refined nonlinear analysis of seismic response characteristics of frame metro station under near-field strong ground motion of large earthquake[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(3): 490-496. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201203020.htm
[4]	王国波. 软土地铁车站结构三维地震响应计算理论与方法的研究[D]. 上海: 同济大学, 2007. WANG Guo-bo. Study on Calculation Theory and Method of Three Dimensional Seismic Response of Subway Station Structures in Soft Soil[D]. Shanghai: Tongji University, 2007. (in Chinese)
[5]	MOK C M, VALLENAS J, ZHANG M, et al. End Wall Effect for Underground Structures: Three-Dimensional Dynamic Soil-Structure Interaction Parametric Study[C]//Proceedings of 100th Anniversary Earthquake Conference Commemorating the 1906 San Francisco Earthquake. 2006.
[6]	HOSSEINI M, ROUDSARI M T. Minimum effective length and modified criteria for damage evaluation of continuous buried straight steel pipelines subjected to seismic waves[J]. Journal of Pipeline Systems Engineering and Practice, 2014, 6(4): 04014018.
[7]	陈清军, 李文婷. 地铁车站–隧道–土相互作用体系地震反应[J]. 地震工程与工程振动, 2018, 38(4): 9-15. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201804002.htm CHEN Qing-jun, LI Wen-ting. Seismic responses analysis of subway station-tunnels-soil-interaction system[J]. Earthquake Engineering and Engineering Vibration, 2018, 38(4): 9-15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201804002.htm
[8]	建筑抗震设计规范：GB 50011—2010[S]. 2010. Code for seismic design of buildings: GB 50011—2010[S]. 2010. (in Chinese)
[9]	季倩倩. 地铁车站结构振动台模型试验研究[D]. 上海: 同济大学, 2002. JI Qian-qian. Shaking Table Testing on Underground Subway Station Structures[D]. Shanghai: Tongji University, 2002. (in Chinese)
[10]	MA Xian-feng, WANG Guo-bo, WU Jun, et al. Experimental study on the seismic response of subway station in soft ground[J]. Journal of Earthquake and Tsunami, 2017, 11(5): 1750020-1-27. doi: 10.1142/S1793431117500208
[11]	赵丁凤, 阮滨, 陈国兴, 等. 基于Davidenkov骨架曲线模型的修正不规则加卸载准则与等效剪应变算法及其验证[J]. 岩土工程学报, 2017, 39(5): 888-895. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705018.htm ZHAO Ding-feng, RUAN Bin, CHEN Guo-xing, et al. Validation of modified irregular loading-unloading rules based on Davidenkov skeleton curve and its equivalent shear strain algorithm implemented in ABAQUS[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(5): 888-895. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705018.htm
[12]	BARD P Y, CHAZELAS J L, GUÉGUEN P, et al. Site-City Interaction[M]. Dordrecht: Springer, 2008: 91-114.

施引文献(3)

期刊类型引用(2)

1.	范雷，余美万，邬爱清，向前. 层间错动带水力耦合抗剪强度特性演化规律研究. 岩土力学. 2023(07): 1959-1970 . 百度学术
2.	武倩宇，韩登林，张吉振，王晨晨，任晓海，林珍珍，苏苗苗，朱亚玲，张娟. 页岩储层中颗粒尺寸效应对微裂缝发育的影响：以威远地区志留系龙马溪组页岩储层为例. 中南大学学报(自然科学版). 2022(09): 3603-3614 . 百度学术