平面P波入射下海底衬砌隧道地震响应解析分析

朱赛男; 李伟华; LeeVincent W; 赵成刚

doi:10.11779/CJGE202008006

平面P波入射下海底衬砌隧道地震响应解析分析 English Version

1.
北京交通大学土木建筑工程学院,北京　100044
2.
University of Southern California,Los Angeles, CA 90089-2531, USA

基金项目:

国家重点基础研究发展计划（“973”计划）项目 2015CB057800

国家自然科学基金项目 51378058

详细信息

作者简介:
朱赛男(1990—),女,博士研究生,主要从事岩土地震工程方面的研究工作。E-mail：15115293@bjtu.edu.cn

通讯作者:
李伟华, E-mail：whli@bjtu.edu.cn

中图分类号: TU435
计量
- 文章访问数: 323
- HTML全文浏览量: 40
- PDF下载量: 121
出版历程
- 收稿日期: 2019-10-11
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-07-31

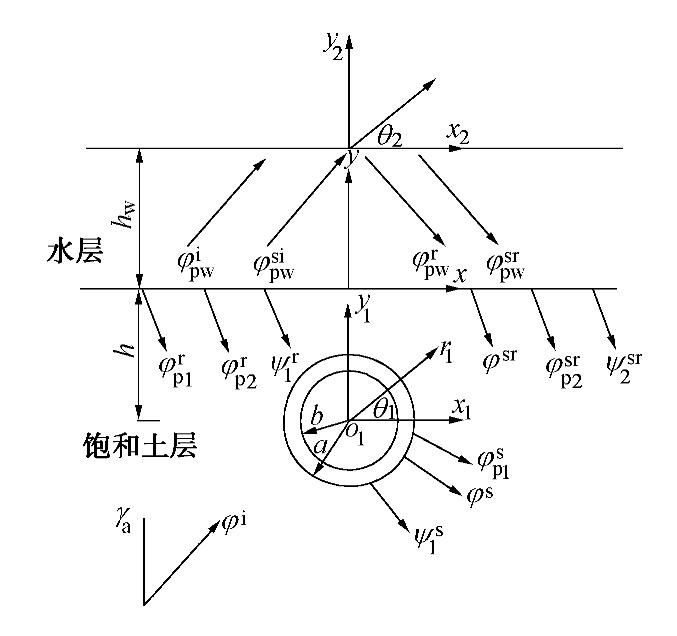
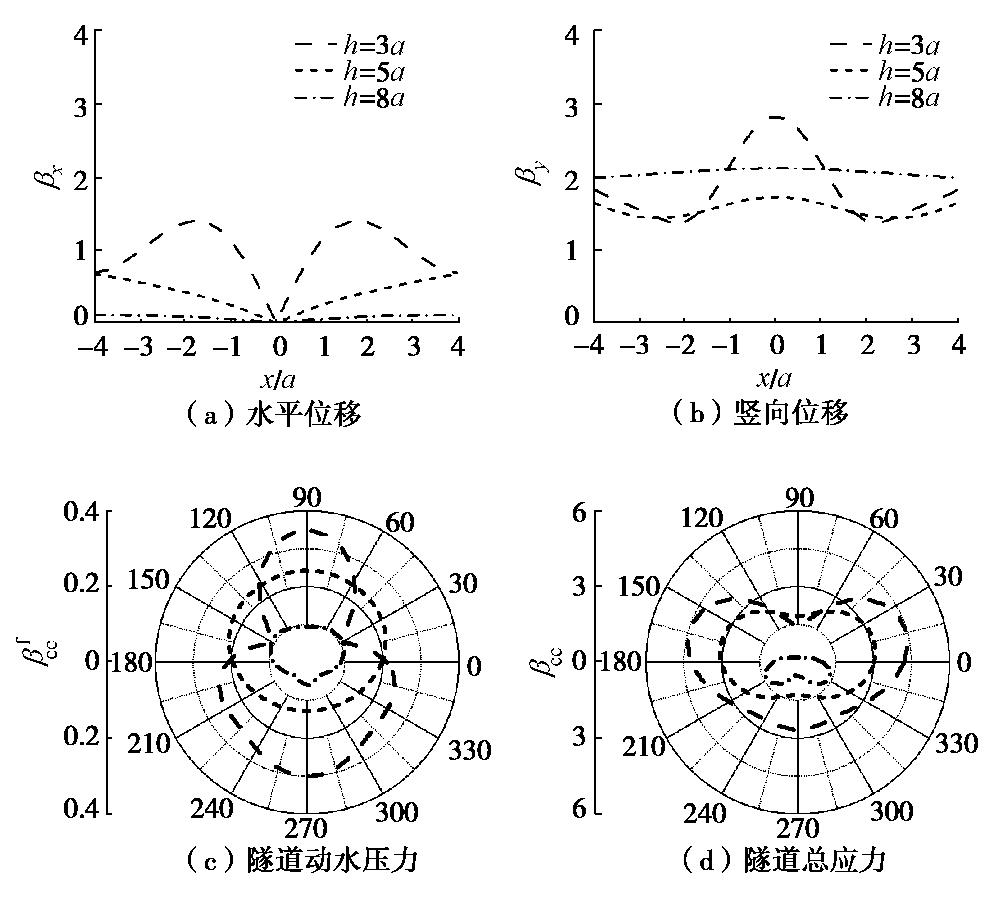
Seismic response of undersea lining tunnels under incident plane P waves

1.
School of Civil Engineering and Architecture, Beijing Jiaotong University, Beijing 100044, China
2.
University of Southern California, Los Angeles, CA 90089-2531, USA

摘要

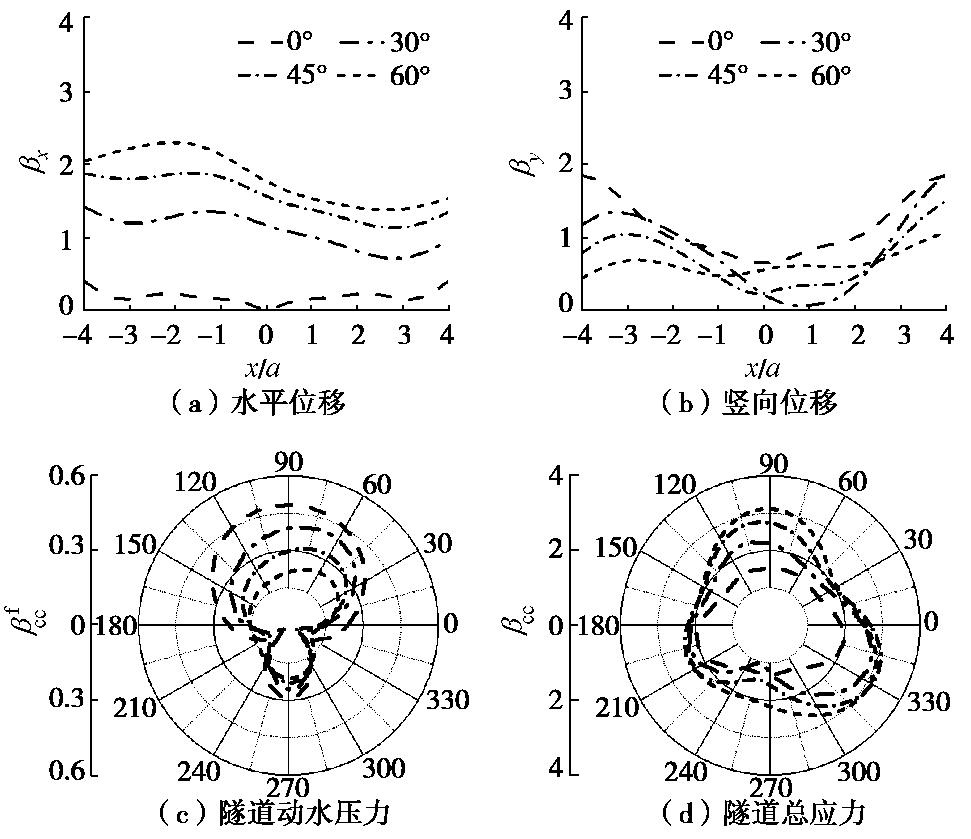
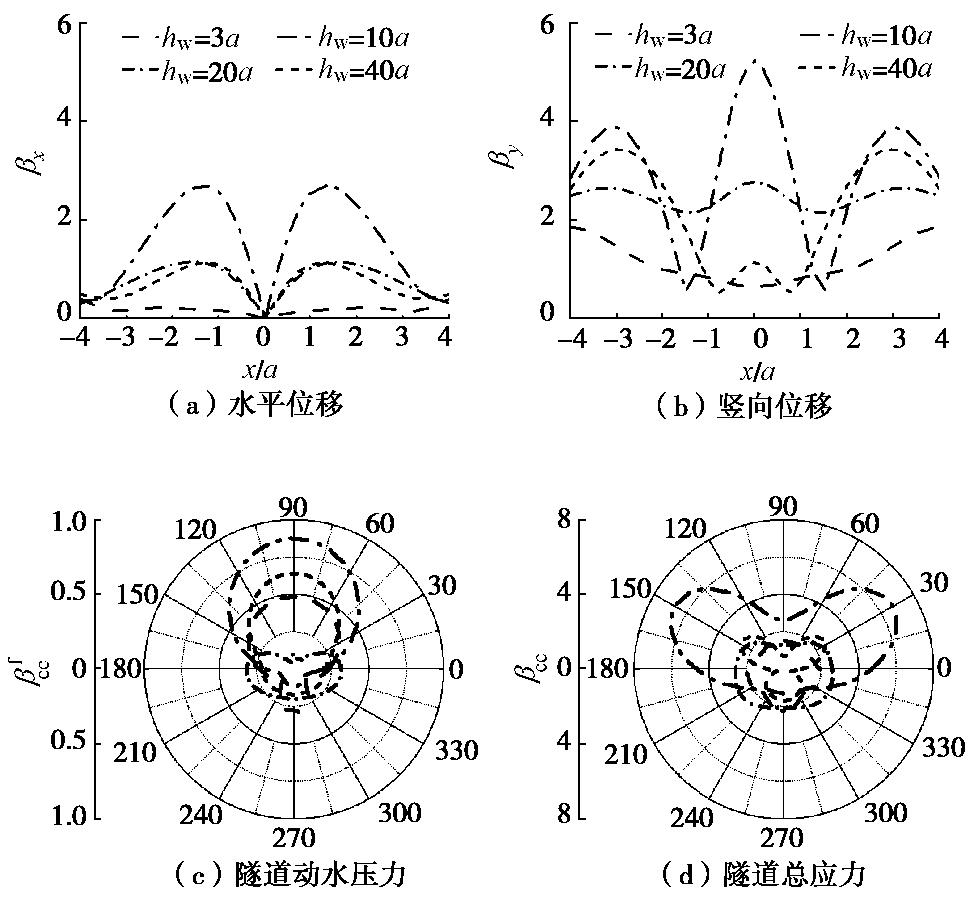
摘要: 基于Biot流体饱和多孔介质和理想流体介质波动理论,采用Hankel函数积分变换法（HFITM）,在考虑水下饱和土的流固耦合及水–土–结构动力相互作用条件下,给出海底衬砌隧道对平面P波散射问题的解析解。Hankel函数积分变换法能够较好地处理半空间表面边界条件,避免了传统研究中的“大圆弧假定”。在解析解的基础上,计算分析了入射角度、入射频率、海水水深和隧道埋深等因素对场地位移和隧道应力的影响。结果表明：入射角度、入射频率、海水水深和隧道埋深对场地位移和隧道应力影响明显；入射角不同时,场地水平位移和隧道动水压力随着入射角的增加而增加,竖向位移和隧道总应力随着入射角的增加而减小；入射频率不同时,隧道应力随着频率的增加而明显减小；海水水深不同时,水深为10倍隧道半径时的场地位移和隧道应力最大；隧道埋深不同时,场地位移和隧道应力随着埋深的增加而减小。
- 海底衬砌隧道 /
- 平面P波 /
- 散射问题 /
- 地震响应 /
- 解析解
Abstract: Based on the wave theory of fluid-saturated porous media by Biot and the ideal wave theory of fluid media, considering the conditions of fluid-solid coupling of undersea saturated soil and seawater-saturated soil-structure dynamic interaction, using the Hankel function integral transformation method (HFITM), an analytical solution is obtained for the scattering problem of incident P waves for an undersea lining tunnel. The Hankel function integral transformation method can better deal with the surface boundary conditions of half space, avoiding the "big arc assumption" in the traditional researches. Based on the analytical solution, the effects of incident angle and incident frequency of P waves, depth of seawater and buried depth of tunnel on site displacement and stress are calculated and analyzed. The results show that the incident angle of P waves, incident infrequency, depth of seawater and buried depth of tunnel have obvious influences on site displacement and tunnel stress. The horizontal displacement of the site and hydrodynamic pressure of the tunnel increase with the increment of incident angle, and the vertical displacement and total tunnel stress decrease with the increment of incident angle. The tunnel stress decreases significantly with the increase of the incident frequency. The site displacement and tunnel stress are the largest when the water depth is 10 times the tunnel radius. The site displacement and tunnel stress decrease with the increasing buried depth.
- undersea lining tunnel /
- plane P wave /
- scattering problem /
- seismic response /
- analytical solution

HTML全文

0. 引言

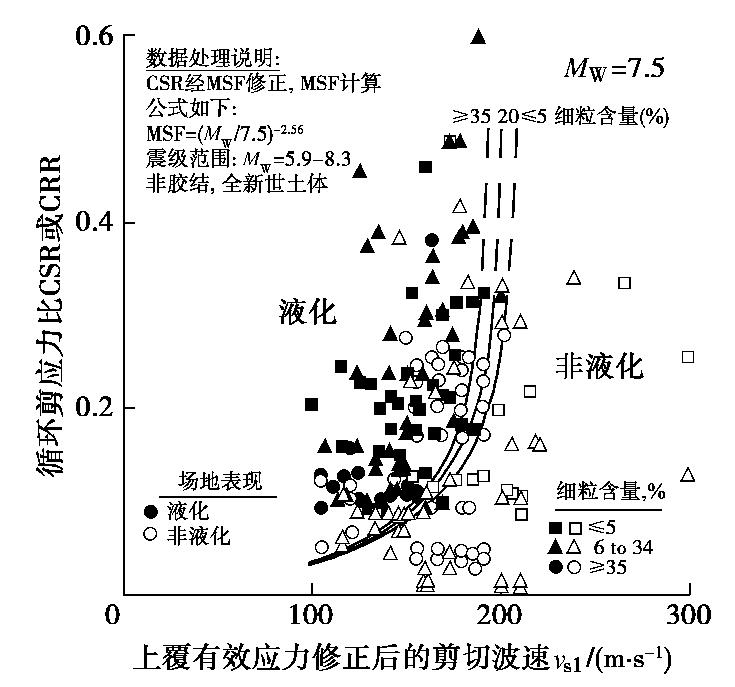
对于饱和砂土地震液化触发判别问题,应用最广泛的Seed简化判别方法主要建立在包含液化宏观震害现象、地震动加速度记录和场地原位测试指标三要素的地震液化实例数据和液化分界线的基础上^[1-3]。以基于原位剪切波速测试指标的液化实例为例,图1给出了地震液化和非液化实例,以及区分液化与否的分界线^[4]。由于强震液化事件彻底破坏易液化土体原有结构性,导致了消除液化土层既往沉积作用的“时钟重置”效应,使得震后获得的场地原位测试指标与真正控制场地抗液化性能的震前土体工程力学特性不对应。考虑到针对地震液化场地的原位测试一般发生在震后数天或数月甚至更长的时间里,图1中地震液化实例数据的剪切波速和相应的液化分界线可能存在与测试时间相关的系统误差。因此,研究震后易液化场地饱和砂土土层的剪切波速（或其它原位测试指标）随时间的变化规律,对正确认识现有基于原位测试指标的液化判别简化方法的可靠性并对震后测试指标进行合理修正具有重要的科学意义。

图 1 基于剪切波速的地震液化实例数据与分界线

Figure 1. v_s-based field case histories and liquefaction boundary curves

下载: 全尺寸图片幻灯片

土体在自然沉积过程中或者经受外荷载剧烈扰动后,其刚度和强度等工程力学参数在恒定应力状态下随时间变化的现象被称为“时间效应”,且该变化可以通过原位测试指标（例如,SPT、CPT和V_s）体现^[5-7]。例如,Andrus等^[8]通过静力触探与剪切波速的经验关系获得了原位砂土剪切波速和完全扰动后剪切波速的比值MEVR,初步揭示了地质时间尺度上的砂土时间效应（见图2）；周燕国等^[9]结合剪切波速（剪切模量）的Hardin公式^[10]和静力触探测试,提出了砂土时间效应的表征指标A_I,并利用不同地质年代砂土实测数据对其表征能力进行了检验。然而,上述研究主要面向地质沉积年代和土性测试指标的经验关系,关注数万年到数十万年甚至更长的地质时间尺度,并没有考虑地质沉积年代中可能受到的各种扰动（如强震事件）对土体工程力学特性的影响。以图2为例,深色椭圆圈内的数据并不符合图中拟合斜线的趋势,而这个时间范围（10^-1～10² a）正是实际工程服役寿命或者高烈度区强震重现周期的范围。Pavlenko等^[11]研究1995年神户地震中场地刚度演化问题,发现液化使得场地刚度急剧降低,但在震后较长一段时间内无法恢复到地震液化前的值。可见,对于实际工程,震后较短的时间尺度内场地土体的时间效应更具有工程意义,是影响易液化场地在余震中的地震响应和再液化可能性的重要因素。

图 2 土体测量与估算剪切波速比的时变趋势

Figure 2. Time variation of measured to estimated velocity ratio

下载: 全尺寸图片幻灯片

针对上述问题,本文对新西兰基督城的REHS强震台站在2010—2011年间的若干强震记录的尾波进行水平与竖向谱比（HVSR）分析,获得了该台站所在的易液化场地在地震前后小应变剪切刚度随时间的发展规律。在此基础上,提出了综合考虑主固结和次固结作用的震后饱和砂土小应变刚度计算模型,并合理预测了REHS台站场地震后刚度恢复变化过程。

1. 场地条件与强震台站记录分析

HVSR方法通过对强震台站的三向加速度记录进行分析得到场地卓越频率以及场地土层结构分布,相比于其它场地频率分析方法,HVSR方法相对简单,能够基本消除震源和传播路径的影响,得到的场地卓越频率更可靠^[12-13]。场地的卓越频率与场地平均剪切波速的关系可表示为^[14]

$v_{savg} = 4 H f$ 。

(1)

式中, $v_{savg}$ 为场地平均剪切波速,H为场地土层厚度,f为场地卓越频率。

根据弹性理论,土体小应变剪切模量表达为

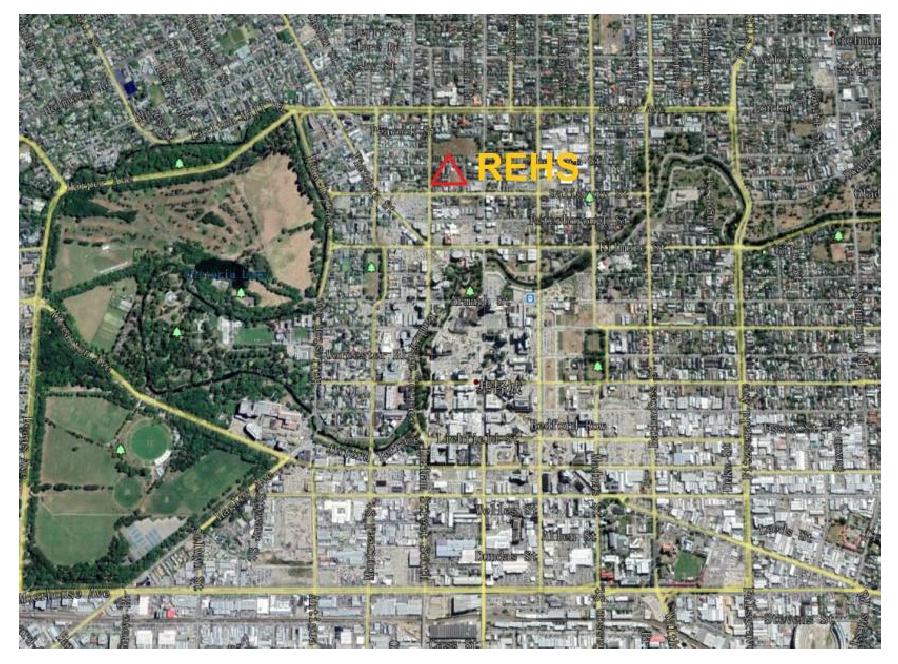
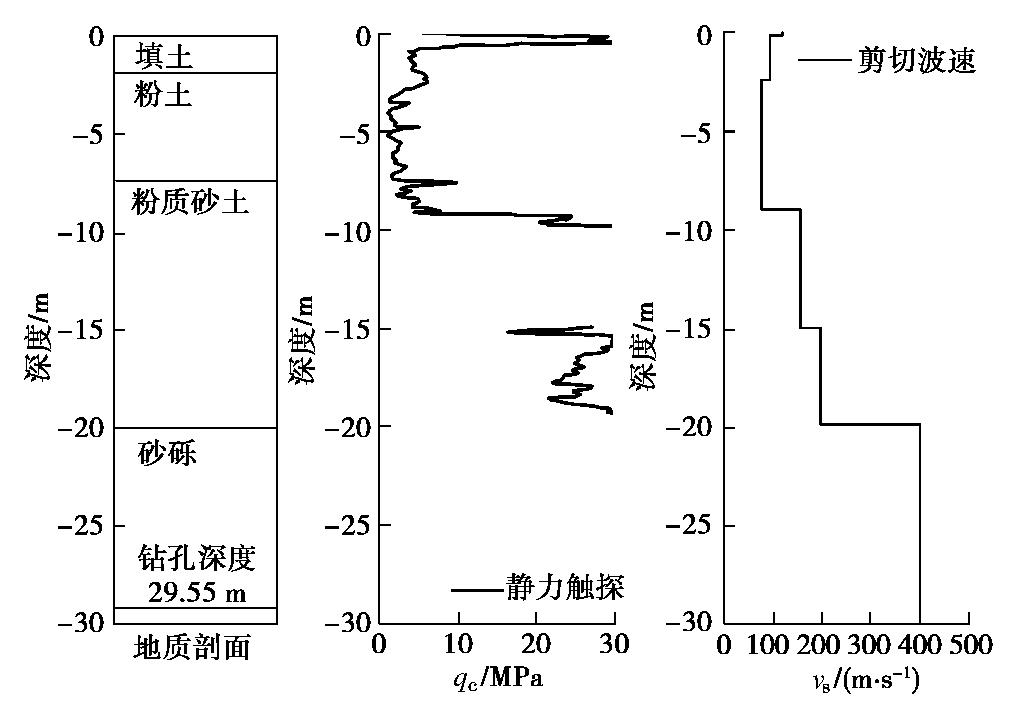
$G_{\max} = ρ \cdot v_{s}^{2}$ 。

(2)

本文针对新西兰基督城CBD区的REHS台站（见图3）,通过触发液化的强震本身和之后发生余震的加速度记录的尾波信号,获得场地卓越频率,根据式（1）,（2）分析从2010年以来3次强震事件之后场地刚度随时间变化规律。REHS台站所处场地的上覆软弱土层厚度约为20 m,存在较厚的饱和粉质砂土层和洁净砂土层,下卧刚度较大的砂卵石层（见图4）,是较典型的易液化场地^[15]。

图 3 基督城REHS强震台站位置（来源：www.nzgd.org.nz）

Figure 3. REHS strong motion station at Christchurch (source: www.nzgd.org.nz)

下载: 全尺寸图片幻灯片

图 4 REHS台站场地土层信息

Figure 4. Soil profile at REHS station site

下载: 全尺寸图片幻灯片

本文采用Geopsy软件进行HVSR分析,该软件能够多窗口同时计算H/V谱比和上覆土层的卓越频率f,并计算它们的平均值和方差。H/V谱比曲线的峰值对应的频率即为该尾波窗口时间对应的卓越频率。图5是尾波窗口选取和计算结果示意图,其中黑色实线代表所有窗口的平均值,两条虚线分别代表它的上、下限,竖向灰色条状区域代表了平均峰值所在的频率段。采用地震动记录的尾波进行HVSR分析获得场地卓越频率需满足一定的条件,即首先要保证主震后的选取的余震强度足够小,一是为了避免该余震事件对场地刚度恢复过程产生额外的显著影响,二是为了尾波段对应场地土体处于小应变弹性应变响应状态；其次,为保证数据处理结果的可靠性,均要求H/V谱比值大于2.0,而且卓越频率的误差在±0.3 Hz以内。

图 5 地震尾波HVSR谱比分析

Figure 5. HVSR analysis of seismic coda wave

下载: 全尺寸图片幻灯片

2. 震后场地小应变刚度演化规律

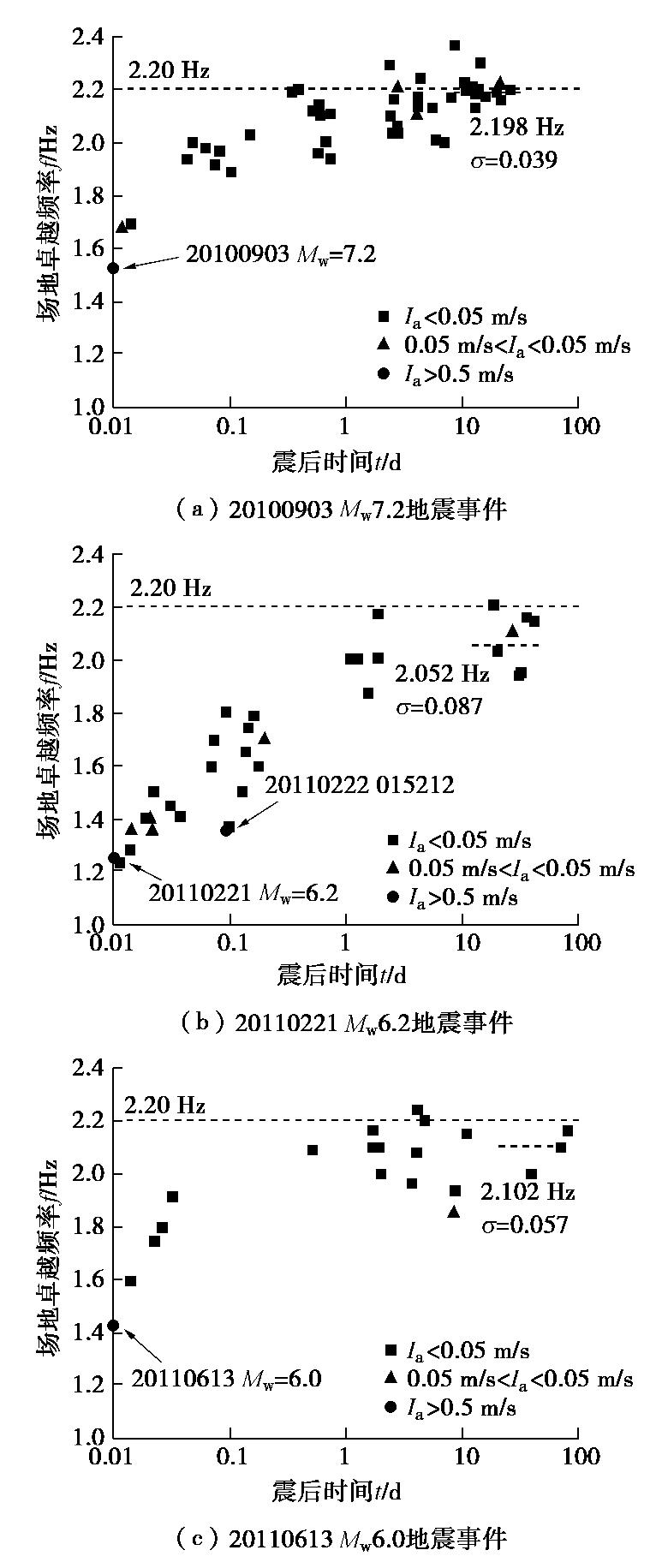
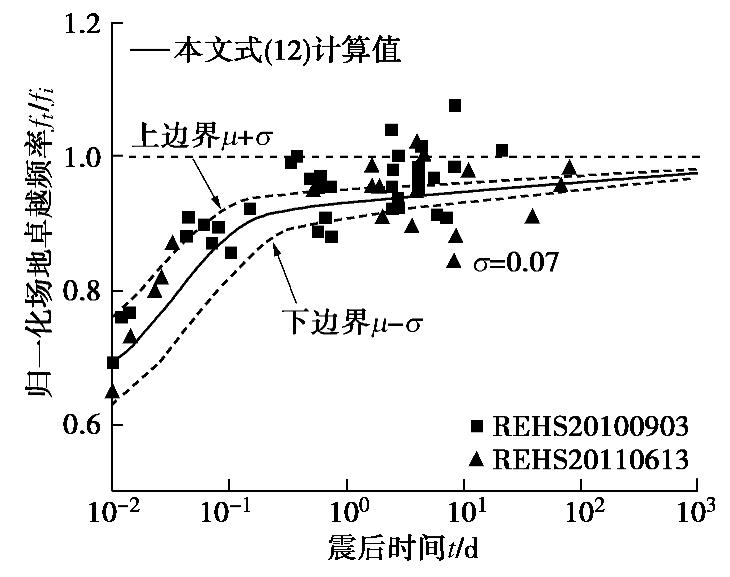
图6给出了REHS台站场地2010年至2011年间3次强震后场地卓越频率随时间的发展情况。考虑到每次强震事件之后大部分余震在台站的地震动强度都很小,可以忽略其对震后场地的进一步扰动作用。每张图上方的黑色虚线代表2010年9月3日M_w7.2地震事件之前场地的卓越频率（f_i=2.20 Hz）,由2010年大震之前的小震记录进行HVSR分析得到；右上角红色虚线表示强震事件后场地的稳定值,可视为下次强震前的场地卓越频率初始值。由图6可见,每次强震后场地刚度恢复至相对稳定的状态所需要的时间基本一致（为数天到数十天）,而且场地稳定后的卓越频率均值接近但低于最初的水平（即2.20 Hz）。

图 6 震后场地卓越频率时变规律

Figure 6. Evolution of fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

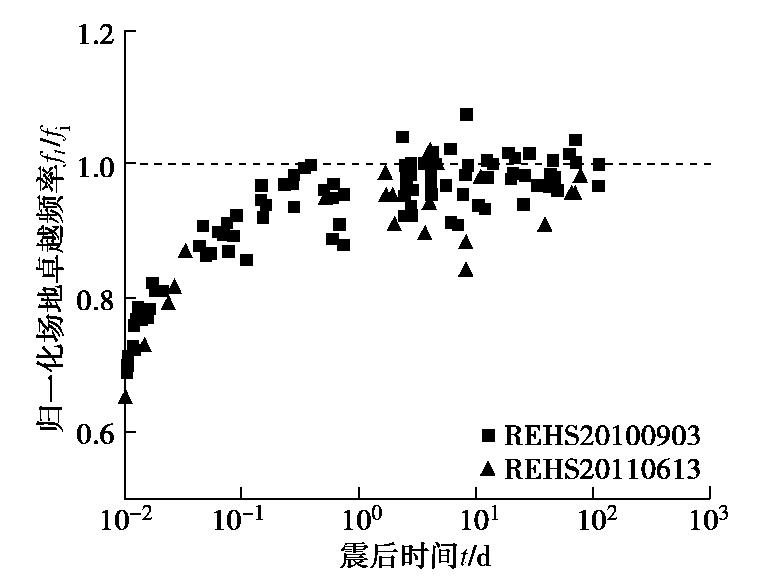
由图6（b）可见,20110221 M_w6.2地震事件中场地卓越频率受到强余震地震历史的影响,因此图7仅将图6（a）和（c）的归一化场地卓越频率（f/f_i）随时间发展规律归纳在一起。由图7可见,震后场地刚度恢复速率基本一致,呈现对数形式的增长,这与PENG等^[16-17]的研究发现类似。而基督城场地小应变刚度在震后10～100 d会有显著的恢复。根据Downes等^[18]的研究,2010年距上次基督城发生强震液化的时间间隔接近100 a,可以认为基督城典型易液化场地的新近沉积时间（或液化的重现周期）为100 a左右,所以尽管REHS台站场地的砂土层刚度在液化后的数月内会有较大的恢复,但仍小于震前水平。需要指出的是,在基督城的其它强震台站（如CBGS和CCCC台站）场地也观测到了类似规律^[19]。另外,注意到图7中同一时间对应的频率数据存在一定离散性,原因包括：首先,HVSR方法不能完全消除震源及传播路径的影响；其次,地震动加速度信号（尤其是小震事件）信噪比水平不同；再次,地下水位的季节性升降等环境变化带来的可能影响。

图 7 震后场地归一化卓越频率变化规律

Figure 7. Evolution of normalized fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

3. 饱和砂土震后小应变刚度计算模型

需要注意,Andrus等^[8]将砂土的MEVR参数用于剪切模量的时间效应修正,这种修正主要反映数十万年甚至更久的由于颗粒胶结引起的时间效应,不能合理反映砂土液化后短期内刚度的变化规律（即孔压消散与次固结引起的时间效应）,而大部分震后实例调查的原位测试均是在这一时间段获得的；其次,这种修正对特定地震和场地数据的依赖性较大,数据十分有限,规律的一般性不强。本节基于饱和砂土的主固结与次固结过程,提出了考虑有效应力变化和砂土颗粒间接触力均质化（包括孔隙比变化）这两个主要因素的震后饱和砂土小应变刚度计算模型。

3.1 主固结影响函数

首先考虑由孔压消散和孔隙变化引起的剪切模量增量,可采用Hardin公式表示土体小应变剪切模量与土体孔隙比及有效应力的关系：

$G_{\max} = A \cdot F (e) {({σ^{'}}_{m})}^{n}$ ,

(3)

式中,G_max为砂土小应变剪切模量,A为结构性参数,F(e)为孔隙比方程, ${σ^{'}}_{m}$ 为平均有效应力,n约等于0.5。

平均固结度U通常定义为

$U = \frac{S_{ct}}{S_{c \infty}}$ ,

(4)

式中,S_ct为地基某时刻的主固结变形,S_c∞为地基的最终主固结变形。

根据太沙基一维固结理论,平均固结度U为

$U = 1 - \sum_{m = 1}^{\infty} \frac{2}{M^{2}} e^{- M^{2} T_{v}}$ 。

(5)

式中,竖向固结时间因子T_v为

$T_{v} = \frac{k_{v} t}{H^{2} γ_{w} m_{v}}$ ,

(6)

式中,k_v为土的竖向渗透系数,t为固结时间,H为土层厚度, $γ_{w}$ 为水的重度,m_v为土体体积压缩模量。

设砂土震后初始孔隙比为e₀,主固结完成后孔隙比为e_c∞,固结中土体孔隙比为e_ct,则由式（4）可以得到土体平均固结度：

$U = \frac{e_{0} - e_{ct}}{e_{0} - e_{c \infty}}$ 。

(7)

超静孔压比与砂土有效应力的关系如下：

$1 - r_{u} (t) = {[\frac{{σ^{'}}_{m, t}}{{σ^{'}}_{m,i}}]}^{2}$ ,

(8)

式中, $r_{u} (t)$ 为t时刻砂土的超静孔压比, ${σ^{'}}_{m, t}$ 为t时刻砂土的有效应力, ${σ^{'}}_{m,i}$ 为砂土的初始最大有效应力。

考虑到在主固结阶段砂土剪切模量增长主要由有效应力增加和孔隙比减小引起的,而结构性变化的影响很小。因此本文假设砂土主固结过程中结构性参数A不变,结合式（3）,（7）,（8）得到砂土震后剪切模量随时间的变化函数如下：

$\frac{G_{pc} (t)}{G_{R}} = \frac{F (e_{0} - U e_{0} + U e_{c \infty})}{F (e_{c \infty})} {[1 - \frac{p_{0}}{σ^{'}} (1 - U)]}^{0.5}$ ,

(9)

式中,G_pc(t)为任意固结时刻的砂土小应变剪切模量,G_R为砂土在参考时间时的小应变剪切模量,一般参考时间t_R大于主固结时间t_p。

3.2 次固结影响函数

砂土次固结过程中,颗粒间接触力均质化（包括孔隙比减小）也是引起砂土刚度随时间增长的一个重要因素^[20-21]。本文采用Howie等^[22]基于室内试验提出的经验公式加以描述：

$\frac{G_{sc} (t)}{G_{R}} = 1 + \frac{Δ G}{G_{R}} \cdot \lg (\frac{t}{t_{R}})$ ,

(10)

式中,t为固结时间,t_R为参考时间,G_sc(t)为任意固结时刻的小应变剪切模量,G_sc,R为在参考时间的小应变剪切模量, $Δ G$ /G_sc,R为剪切模量增长速率,对于特定的土体需根据室内固结试验确定。

3.3 饱和砂土震后小应变刚度计算模型

在震后一定的时间段,砂土剪切模量变化受上述两个因素共同影响,本文假设这两种机理相互独立,结合式（9）,（10）得

$\frac{G (t)}{G_{R}} = 1 + \frac{Δ G_{pc} (t)}{G_{R}} + \frac{Δ G_{sc} (t)}{G_{R}}$ 。

(11)

式（11）结合 $G = ρ v_{s}^{2}$ 和 $v_{s} = 4 H f$ 可得到场地卓越频率随随时间发展的函数：

$\frac{f (t)}{f_{R}} = \sqrt{\frac{G (t)}{G_{R}}}$ 。

(12)

根据现有围绕基督城场地的研究成果,式（12）的参数取值如下：该场地上覆软弱土层厚20 m,主要由砂土和粉土组成,排水条件良好^[15]；根据CPT测试的I_c和渗透系数的经验关系^[23]取土层平均渗透系数k_v=2.5×10^-5 m/s；土层的平均压缩模量由动力触探锤击数与压缩模量的经验关系^[24]得到,取E_s=15.0 MPa；土层初始平均超静孔压比取p₀=0.8。另外,假设震后场地刚度需要经历震前同样的沉积时间才能恢复至2010年9月3日强震液化事件之前的震前值,则参考时间取为t_R=100 a。

根据式（12）计算得到基督城REHS台站场地液化后基频随时间的发展规律如图8中的曲线所示,图中上、下两条边界线代表由于参数取值带来的标准差。由图8可见,该计算模型对图6（a）,（c）中的两次强震数据的预测效果较好,能够考虑震后一定时间内饱和砂土刚度的恢复规律。

图 8 震后刚度发展函数预测效果

Figure 8. Prediction of post-earthquake stiffness function

下载: 全尺寸图片幻灯片

4. 结论

为研究震后饱和砂土场地原位测试指标变化规律及其与震前值的差异,本文针对新西兰基督城的典型易液化场地,开展了从实际场地卓越频率监测分析到砂土小应变刚度计算模型的研究。主要结论如下：

（1）针对基督城系列强震,对REHS强震台站记录信号进行HVSR分析,揭示了震后场地刚度整体呈现指数形式的增长规律。场地小应变刚度会在震后经过数天的快速恢复后进入相对稳定的缓慢上升期。对于震前沉积时间较久的场地,场地刚度在震后短时间内难以恢复到震前水平,现有基于震后原位调查获得的液化实例数据应当根据震后原位测试时间进行适当的修正。

（2）假设震后场地刚度需要经历震前同样的沉积时间才能恢复至震前值,基于主固结与次固结过程提出了具有物理意义的饱和砂土震后小应变刚度计算模型,可估算基督城典型易液化场地在强震后平均小应变刚度随时间的发展规律。该计算模型为将特定场地的震后原位测试指标（如剪切波速）修正到对应的震前值提供了一种有效手段。

注意到本文所揭示的震后场地小应变刚度演化规律和所建议的计算模型及参数主要针对新西兰基督城场地,有必要进一步研究更多的其它地震和场地刚度演化规律,并获取各类易液化场地和土体参数,才能为将液化实例中的震后原位测试指标修正到震前原状土的对应值提供定量依据,提高当前基于液化实例调查的地震液化简化判别方法的准确性。

图 1 分析模型

Figure 1. Analysis model

下载: 全尺寸图片幻灯片

图 2 退化饱和土衬砌隧道模型

Figure 2. Degradation to model for saturated soil lining tunnel

下载: 全尺寸图片幻灯片

图 3 不同入射角下的场地位移和隧道应力

Figure 3. Site displacements and tunnel stresses under different incident angles

下载: 全尺寸图片幻灯片

图 4 不同频率下的场地位移和隧道应力

Figure 4. Site displacements and tunnel stresses under different incident frequencies

下载: 全尺寸图片幻灯片

图 5 不同水深的场地位移和隧道应力

Figure 5. Site displacements and tunnel stresses under different depths of seawater

下载: 全尺寸图片幻灯片

图 6 不同隧道埋深的场地位移和隧道应力

Figure 6. Site displacements and tunnel stresses under different buried depths of tunnel

下载: 全尺寸图片幻灯片

参考文献(26)

[1]	朱镜清, 周建. 海底隧道体系地震反应分析方法[J]. 地震工程与工程振动, 1992, 12(2): 90-98. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199202009.htm ZHU Jing-qing, ZHOU Jian. A seismic analysis method of undersea tunnels[J]. Earthquake Engineering and Engineering Vibration, 1992, 12(2): 90-98. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199202009.htm
[2]	朱镜清, 李金成. 海水对海底地震动的影响问题[C]//中国地震学会第四次学术大会论文摘要集, 1992, 北京. ZHU Jing-qing, LI Jin-cheng. Problem of effects of seawater onundersea ground seismic motion[C]//Proc of China Seismological Society of the 4th Academic Conference, 1992, Beijing. (in Chinese)
[3]	朱镜清, 周建. 海底地震动估计的一个流体力学基础[J]. 地震工程与工程振动, 1991, 11(3): 87-93. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199103007.htm ZHU Jing-qing, ZHOU Jian. A fluid mechanics basis for estimating undersea ground motion[J]. Earthquake Engineering and Engineering Vibration, 1991, 11(3): 87-93. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199103007.htm
[4]	朱镜清, 周建, 朱达力. 海底淤泥层对海洋工程地震作用环境的影响问题[J]. 地震工程与工程振动, 1999, 19(3): 1-6. doi: 10.3969/j.issn.1000-1301.1999.03.001 ZHU Jing-qing, ZHOU Jian, ZHU Da-li. Problem of effects of seafloor silt on earthquake action environment of ocean engineering[J]. Earthquake Engineering and Engineering Vibration, 1999, 19(3): 1-6. (in Chinese) doi: 10.3969/j.issn.1000-1301.1999.03.001
[5]	朱镜清. 地震作用下海水与海床土的耦合运动[J]. 地震工程与工程振动, 1988, 8(2): 37-43. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC198802004.htm ZHU Jing-qing. Coupled motion between sea water and sea bed-soil under earthquake action[J]. Earthquake Engineering and Engineering Vibration, 1988, 8(2): 37-43. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC198802004.htm
[6]	陈向红, 张鸿儒. 暗挖海底隧道地震动水压力响应分析[J]. 北京交通大学学报, 2012, 36(1): 36-40. doi: 10.3969/j.issn.1673-0291.2012.01.007 CHEN Xiang-hong, ZHANG Hong-ru. Analysis of effect of hydrodynamic pressure on undersea tunnels constructed by excavation method[J]. Journal of Beijing Jiaotong University, 2012, 36(1): 36-40. (in Chinese) doi: 10.3969/j.issn.1673-0291.2012.01.007
[7]	栾茂田, 张小玲, 张其一. 地震荷载作用下海底管线周围砂质海床的稳定性分析[J]. 岩石力学与工程学报, 2008, 27(6): 1155-1161. doi: 10.3321/j.issn:1000-6915.2008.06.008 LUAN Mao-tian, ZHANG Xiao-ling, ZHANG Qi-yi. Stability analysis of sandy seabed around submarine pipelines under seismic load[J]. Chines Journal of Rock Mechanics and Engineering, 2008, 27(6): 1155-1161. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.06.008
[8]	席仁强, 陈国兴, 王志华. 覆水场地地震反应分析[J]. 防灾减灾工程学报, 2009, 29(6): 610-617. doi: 10.3969/j.issn.1672-2132.2009.06.003 XI Ren-qiang, CHEN Guo-xing, WANG Zhi-hua. Seismic response of underwater site[J]. Journal of Disaster Prevention and Mitigation Engineering, 2009, 29(6): 610-617. (in Chinese) doi: 10.3969/j.issn.1672-2132.2009.06.003
[9]	程选生, 王建华, 杜修力. 渗流作用下海底隧道的流–固耦合地震响应分析[J]. 现代隧道技术, 2013, 50(6): 44-51. doi: 10.3969/j.issn.1009-6582.2013.06.008 CHENG Xuan-sheng, WANG Jian-hua, DU Xiu-li. Fluid-solid coupling based seismic response analysis of seabed tunnels during seepage[J]. Modern Tunnelling Technology, 2013, 50(6): 44-51. (in Chinese) doi: 10.3969/j.issn.1009-6582.2013.06.008
[10]	刘继国, 程勇, 郭小红. 海底盾构隧道地震响应影响因素分析[J]. 中外公路, 2011, 31(4): 200-203. https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201104052.htm LIU Ji-guo, CHENG Yong, GUO Xiao-hong. Analysis of factors affecting seismic response of seabed shield tunnel[J]. Journal of China & Foreign Highway, 2011, 31(4): 200-203. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201104052.htm
[11]	周鹏, 崔杰, 李亚东, 等. 地震P波斜入射下入射角度对海底沉管隧道结构动力响应的影响[J]. 世界地震工程, 2016(3): 78-85. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201603013.htm ZHOU Peng, CUI Jie, LI Ya-dong, et al. Effect of oblique incident angle of P-wave on submarine immersed tunnels[J]. Word Earthquake Engineering, 2016(3): 78-85. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201603013.htm
[12]	巨建民, 李会鹏. P波斜入射下海底沉管隧道地震响应分析[J]. 大连交通大学学报, 2018, 39(6): 115-119. https://www.cnki.com.cn/Article/CJFDTOTAL-DLTD201806023.htm JU Jian-min, LI Hui-peng. Seismic response analysis of submarine immersed tunnel to P-wave of oblique incidence[J]. Journal of Dalian Jiaotong University, 2018, 39(6): 115-119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DLTD201806023.htm
[13]	郭崇峙. 水下隧道地基地震变形特征与结构地震响应分析[D]. 北京: 北京交通大学, 2013. GUO Chong-zhi. Analytical Solution and Numeric Analysis of Seismic Response of the Stratum and Tunnel Under Water[D]. Beijing: Beijing Jiaotong University, 2013. (in Chinese)
[14]	赵成刚, 王进廷, 史培新, 等. 流体饱和两相多孔介质动力反应分析的显式有限元法[J]. 岩土工程学报, 2001, 23(2): 178-182. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200102009.htm ZHAO Cheng-gang, WANG Jin-ting, SHI Pei-xin, et al. Dynamic analysis of fluid-saturated porous media by using explicit finite element method[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(2): 178-182. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200102009.htm
[15]	LEE V W. On deformations near circular underground cavity subjected to incident plane SH waves[C]//Proceedings of the Application of Computer Methods in Engineering Conference, 1997, Los Angeles: 951-962.
[16]	马宏伟, 陈文化. 大型引水隧道在平面地震波入射下动力响应的解析解[J]. 地震工程与工程振动, 2011, 31(6): 1-10. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201106001.htm MA Hong-wei, CHEN Wen-hua. Analytic solution for seismic responses of large-span diversion tunnel induced by plane seismic waves[J]. Earthquake Engineering and Engineering Vibration, 2011, 31(6): 1-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201106001.htm
[17]	马宏伟, 陈文化, 宗琦, 等. P波入射引起的水下输水隧洞地震响应研究[J]. 世界地震工程, 2016(4): 196-204. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201604029.htm MA Hong-wei, CHEN Wen-hua, ZONG Qi, et al. Study on seismic response of underwater convey tunnel induced by plane P waves[J]. Word Earthquake Engineering, 2016(4): 196-204. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201604029.htm
[18]	马宏伟, 陈文化, 宗琦. SV波引起的水下输水隧洞平面地震响应研究[J]. 防灾减灾工程学报, 2016(5): 82-88. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201605012.htm MA Hong-wei, CHEN Wen-hua, ZONG Qi. Transverse response of underwater convey tunnel to incident SV waves[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016(5): 82-88. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201605012.htm
[19]	丁曼曼. 水下盾构隧道饱和砂层地震响应的平面解析分析[D]. 北京: 北京交通大学, 2009. DING Man-man. Plane Analysis of Seismic Response of the Underwater Saturated Sandy Subsoil with Shield Tunnel[D]. Beijing: Beijing Jiaotong University, 2013. (in Chinese)
[20]	BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid: I low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168.
[21]	LIN C H, LEE V W, TODOROVSKA M I, et al. Zero-stress, cylindrical wave functions around a circular underground tunnel in a flat, elastic half-space: incident P-waves[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(10): 879-894.
[22]	LAMB H. On the propagation of tremors over the surface of an elastic solid[J]. Philosophical Transactions of the Royal Society of London, 1904, 203: 1-42.
[23]	DERESIEWICZ H. The effect of boundaries on wave propagation in a liquid-filled porous solid: I reflection of plane waves at a free plane boundary (non-dissipative case)[J]. Bull Seismol Soc Am, 1960, 50(4): 599-607.
[24]	LIN C H, LEE V W, TRIFUNAC M D. The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid[J]. Soil Dynamics & Earthquake Engineering, 2005, 25(3): 205-223.
[25]	叶其孝, 沈永欢. 实用数学手册[M]. 北京: 科学出版社, 2006. YE Qi-xiao, SHEN Yong-huan. Practical Math Manual[M]. Beijing: Science Press, 2006. (in Chinese)
[26]	LIU Z, JU X, WU C, et al. Scattering of plane P1waves and dynamic stress concentration by a lined tunnel in a fluid-saturated poroelastic half-space[J]. Tunnelling & Underground Space Technology, 2017, 67: 71-84.

施引文献(2)

期刊类型引用(2)

1.	刘志文，王媛，董琪，高山. 不连续界面渗流的堤防防渗膜防渗效果模拟研究. 人民黄河. 2024(06): 48-53+67 . 百度学术
2.	张升，兰鹏，苏晶晶，熊海斌. 基于PINNs算法的地下水渗流模型求解及参数反演. 岩土工程学报. 2023(02): 376-383+443-444 . 本站查看