软硬互层岩质反倾边坡弯曲倾倒离心模型试验与数值模拟研究

黄达; 马昊; 孟秋杰; 宋宜祥

doi:10.11779/CJGE202007012

软硬互层岩质反倾边坡弯曲倾倒离心模型试验与数值模拟研究 English Version

黄达^{1, 2, 3,},
马昊^2, ,,
孟秋杰³,
宋宜祥³

1.
长安大学地质工程与测绘学院,陕西　西安　710054
2.
重庆大学土木工程学院,重庆　400044
3.
河北工业大学土木与交通学院,天津　300401

基金项目:

国家自然科学基金面上项目 41672300

国家自然科学基金面上项目 41972297

详细信息

作者简介:
黄达(1976—),男,教授,博士生导师,主要从事边坡工程与地质灾害方向的研究工作。E-mail：hdcqy@126.com

通讯作者:
马昊, E-mail：mahgeo@126.com

中图分类号: TU43
计量
- 文章访问数: 318
- HTML全文浏览量: 30
- PDF下载量: 164
出版历程
- 收稿日期: 2019-07-22
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-06-30

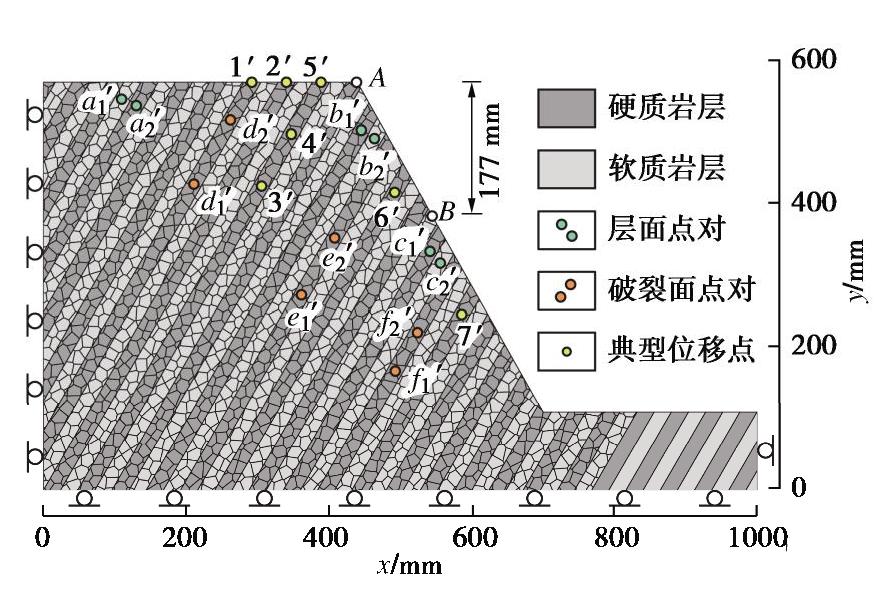
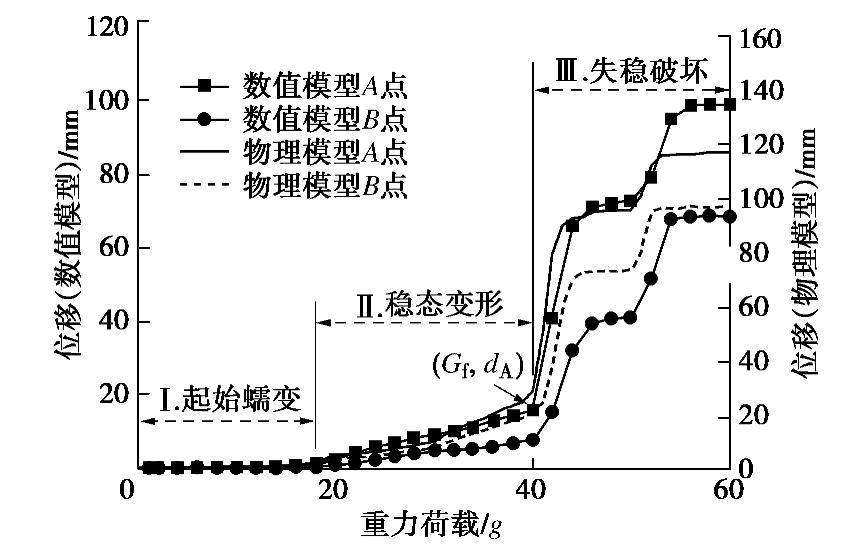
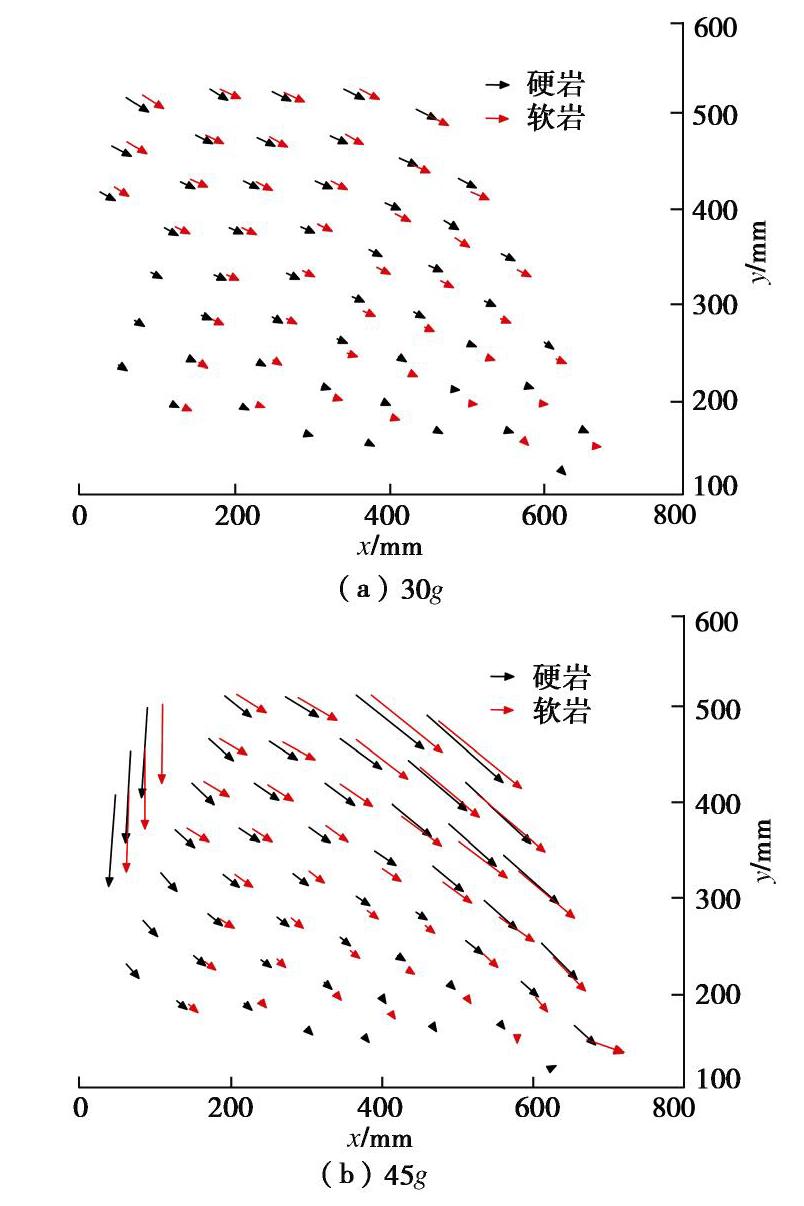
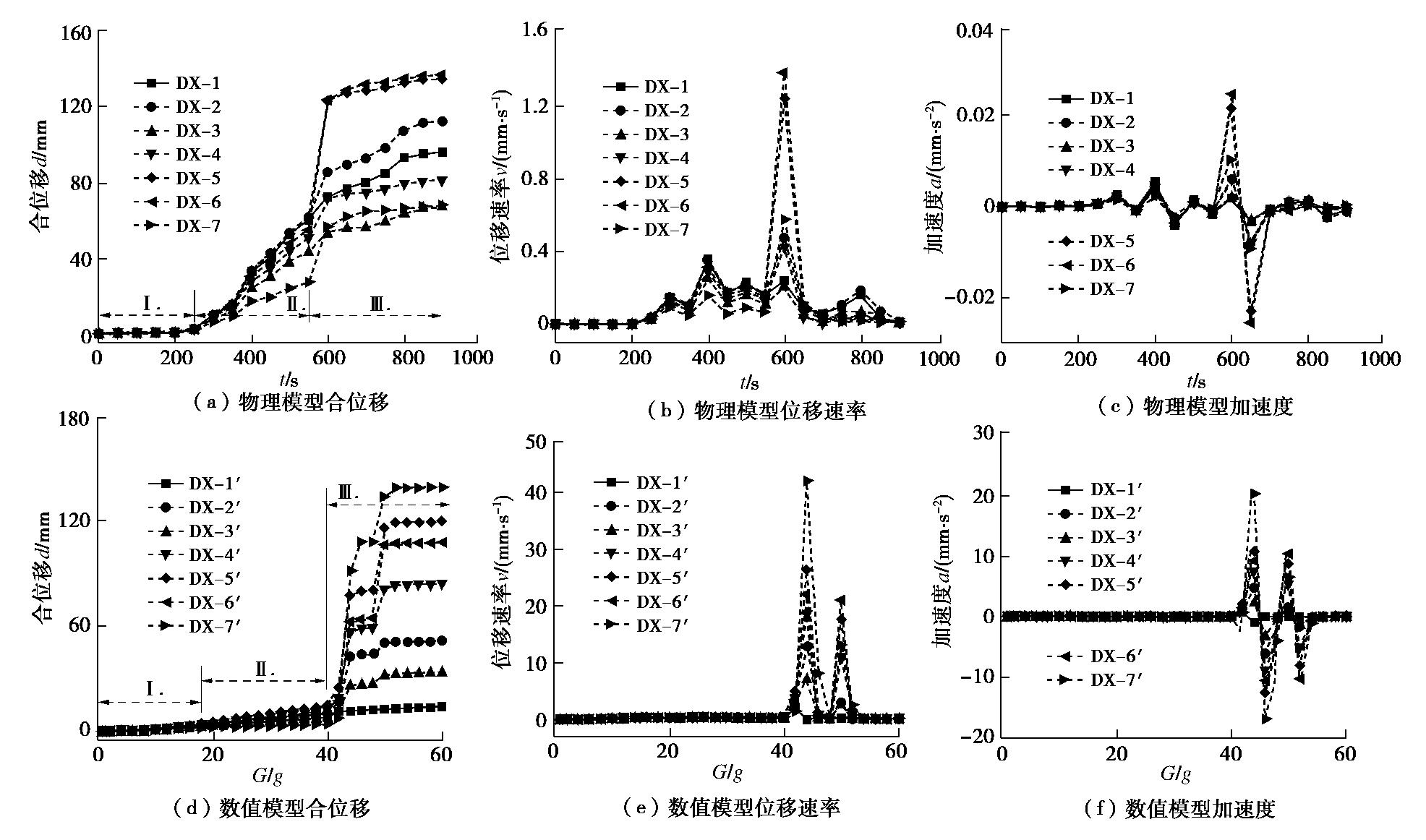
Centrifugal model test and numerical simulation for anaclinal rock slopes with soft-hard interbedded structures

HUANG Da^{1, 2, 3,},
MA Hao^2, ,,
MENG Qiu-jie³,
SONG Yi-xiang³

1.
College of Geological Engineering and Geomatics, Chang'an University, Xi'an 710054, China
2.
School of Civil Engineering, Chongqing University, Chongqing 400044, China
3.
School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China

摘要

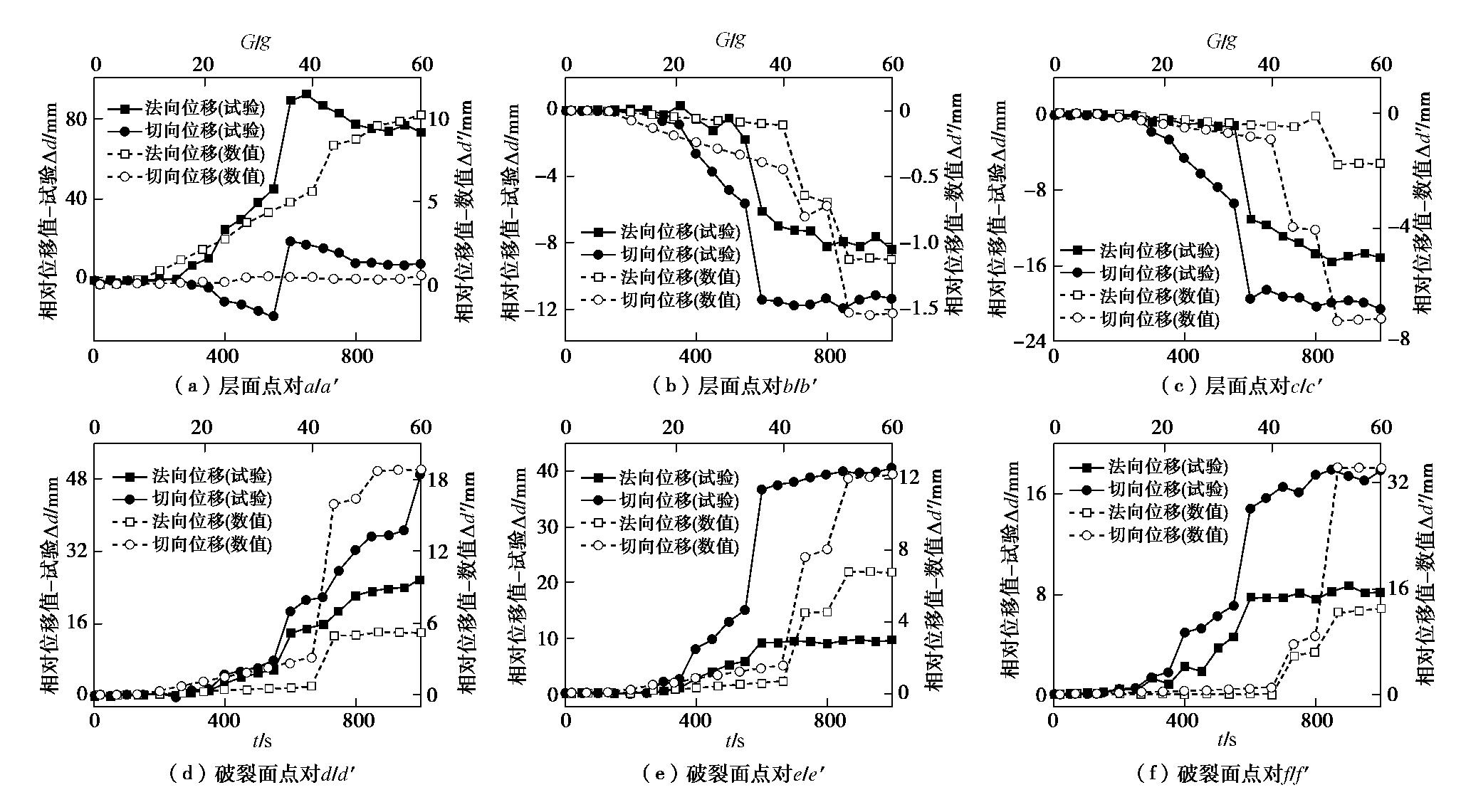
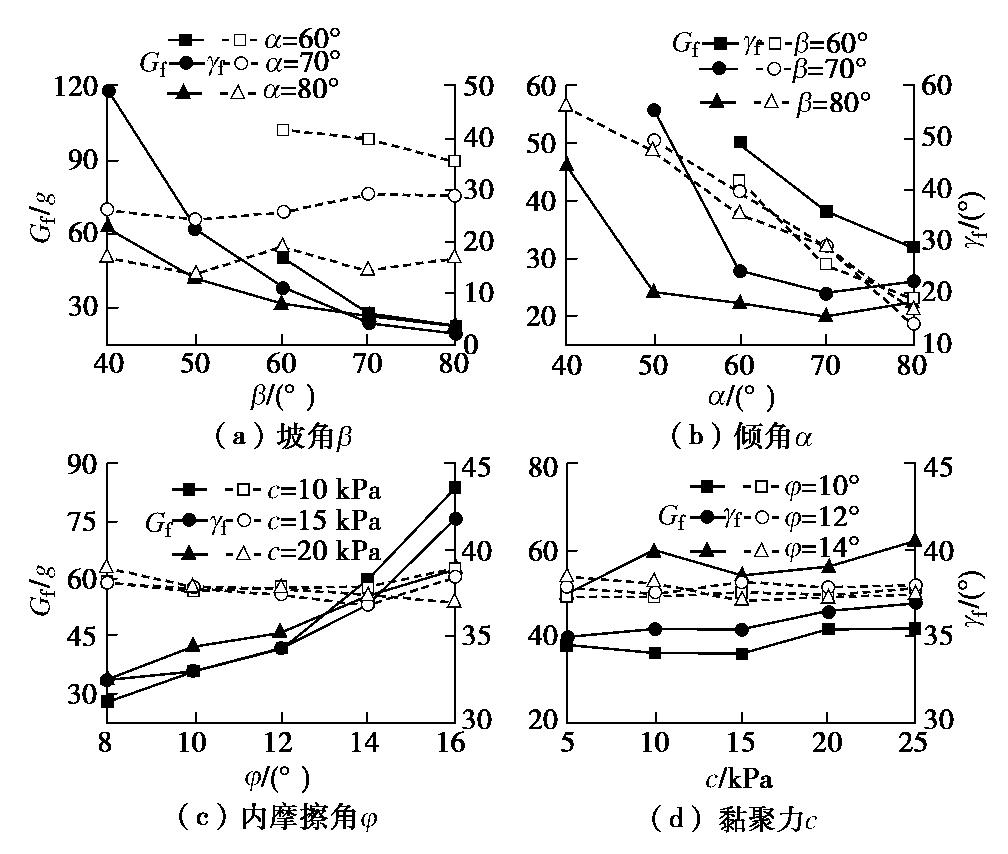
摘要: 西部山区工程建设揭露了众多大型弯曲倾倒变形体,多具有软硬互层结构,水平深度可达300 m。为进一步探明软硬互层反倾边坡的倾倒变形机制,融合离心模型试验与UDEC模拟,研究了此类边坡的破坏模式与影响因素,并通过点对分析,讨论了变形的力学机制。数值模拟时,在岩层内预置随机裂隙,获得了破裂面的演化规律。结果表明：数值模拟与试验的位移曲线及破裂面形态吻合较好,边坡变形可分为起始蠕变阶段、稳态变形阶段和失稳破坏阶段；坡体前部为压剪复合变形,后部则以拉张为主；边坡主破裂面呈弧形,由坡脚快速贯通至坡顶,整体为拉–剪性破裂面；坡体内发育3条破裂面,可作为分界线将变形体分为极强倾倒区、强倾倒区和弱倾倒区；坡脚岩体变形后期压致拉裂,逐渐折断脱离母岩,最终导致变形岩体沿不同的破裂面形成渐进后退式破坏；边坡在倾角与坡角之和大于等于120°时才较易破坏,坡角主要影响破坏难易,倾角则控制变形规模。
- 反倾边坡 /
- 软硬互层 /
- 倾倒变形 /
- 离心模型试验 /
- 离散元数值模拟
Abstract: Most of the toppling deformations exposed in western China have soft-hard interlayer structures. The maximum depth even reaches 300 m. In order to further explore the toppling mechanism of soft-hard interbedded anaclinal slope, centrifugal model tests and UDEC simulation are combined. The mechanical mechanism of toppling is analyzed through point-to-point relative displacement. Random fissures are preset in rock plates of numerical slopes, and the evolution laws of failure surface are obtained. The results show that the displacement and fracture morphology of numerical model agree well with physical tests. The toppling process of slope can be divided into initial creep stage, steady deformation stage and failure stage. The front part of the slope is compression-shear composite deformation, while the rear part is tension-dominated. The main fracture surface runs through the whole slope rapidly from the slope toe with a curved shape, and is a tension-shear fracture surface. There are three fracture surfaces in the slope, which can be used as borders to divide the toppling slope into extremely strong toppling zone, strong toppling zone and weak toppling zone. At the anaphase of the deformation, the failure mode of slope toe turns into compression cracking, and the toe rocks gradually separate from parent rocks, leading to the progressive retrogressive failure of slope along different fracture surfaces. The slope is more likely to be damaged when the sum of the dip and slope angle is greater than or equal to 120°. The slope angle mainly affects the damage degree, and the dip controls the deformation scale.
- anaclinal slope /
- soft-hard interbedded structure /
- toppling deformation /
- centrifugal model test /
- DEM

HTML全文

0. 引言

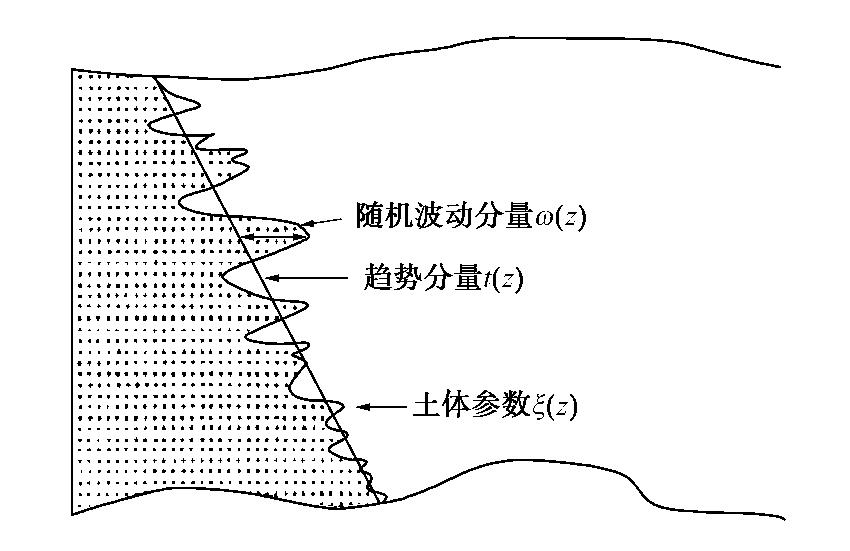
由于沉积条件、应力历史、风化程度、埋藏条件以及其它地质作用的差异,岩土工程中土性参数具有显著的空间变异性,而由于所经历的地质、化学和环境作用的差异,土性参数整体又呈现沿埋深变化的波动性和趋势性。上述岩土参数的空间变异性对岩土工程尤其是边坡稳定可靠性的影响已广为学术界和工程界关注^[1]。对于绝大多数边坡稳定性研究,平稳随机场常用来表征土性参数的空间变异性^[2]。然而大量现场试验和相关试验数据表明,土性参数如黏聚力、内摩擦角、土壤重度以及不排水抗剪强度等的统计特征参数沿土体埋深呈现明显的非均匀分布特征。如王长虹等^[3]统计表明,天津地铁^#5、^#6线环湖西路站—宾馆西路站四线隧道交叠区间断面黏聚力和内摩擦角均值随埋深非连续性变化,具有间断性。Jaksa等^[4]和Cafaro等^[5]分别调查了澳大利亚南部某港市典型地层和意大利塔兰托地区典型地层,显示剖面黏土层的锥尖阻力 $q_{c}$ 沿埋深具有明显的分层特性。林军等^[6]和Chenari等^[7]调查发现江苏海相黏土 $q_{c}$ 和乌尔米耶湖场地黏土 $q_{c}$ 沿深度方向同样呈现明显的分层趋势。由此可见,忽略土性参数均值和标准差随埋深非连续性变化的趋势而建立的平稳随机场用来表征土性参数的空间变异性是不合理的。

土性参数的统计特征参数沿埋深方向的非均匀分布特征对岩土结构可靠度有重要影响,有学者对此进行了有益探索。Griffiths等^[8]在考虑不排水抗剪强度均值和标准差沿埋深线性增加的前提下,采用随机有限元法分析了边坡可靠度问题；祁小辉等^[9]探讨了不排水抗剪强度统计特征参数的非均匀分布特征对条形地基极限承载力影响；Wu等^[10]采用非平稳随机场模拟了不排水抗剪强度的空间变异性对深基坑开挖稳定可靠度的影响；蒋水华等^[11]提出了不排水抗剪强度的非平稳随机场模型,讨论了不排水抗剪强度的统计特征参数的非均匀分布特征对边坡可靠度的影响规律。以上学者的研究均采用趋势分量和随机波动分量来表征土性参数的非平稳性,考虑了趋势分量的不确定性或随机波动分量的不确定性,从而建立的非平稳随机场。该方法不足之处在于只适于同类土或相似土构成的边坡,对于不同类别土壤构成的边坡,会导致对土性参数变异性的不准确估计。

为此,本文提出了多涨落尺度（fluctuation scale,为免与物理中的波动混淆,在此称为涨落尺度）^[12]的土性参数分层非平稳随机场模型。该模型主要针对多种类型土壤组成的边坡土性参数的统计特征参数的非连续的非平稳特性。与现有平稳随机场模型和其他非平稳随机场模型的比较显示,所建模型可合理描述土性参数的分层特性。通过一实际工程边坡算例验证了所建模型的有效性,并研究了黏聚力和内摩擦角的统计特征参数的非连续非平稳特征对临界滑移面形状、位置以及边坡稳定可靠度的影响。

1. 统计参数连续变化的非平稳随机场

若参数的均值与方差不随土体空间位置而变化,其协方差函数只与空间两点的相对位置有关,而与绝对位置无关,则认为土性参数随机场是平稳或均匀的（homogeneous random field,记作HRF）,由参数均值、方差、相关函数或相关长度即可构建一个平稳随机场^[13]。若土性参数的协方差函数与空间两点的绝对位置有关,则为非平稳或非均匀随机场（non- homogeneous random field,即NHRF）。根据参数统计特性随深度的变化情况,目前已有的土性参数随机场主要包括均值和标准差沿深度不变的平稳随机场；均值随深度线性增加而标准差不变的非平稳随机场以及均值与标准差均随深度线性增加的非平稳随机场^[14]。

边坡工程研究采用较多的是参数平稳随机场模型,然而大量原位测试与试验数据统计分析表明,土性参数的统计特征参数存在非平稳性,特别体现在沿深度方向的趋势性与随机波动性,如图1所示。

图 1 土性参数的统计特征参数沿埋深的变异性

Figure 1. Variability of statistical characteristic parameters of soil parameters with depth

下载: 全尺寸图片幻灯片

土性参数 $ζ (z)$ 沿深度的变化可以表示为

$ζ (z) = t (z) + ω (z)$ ,

(1)

式中, $z$ 为土体埋深, $t (z)$ 为趋势分量函数,如土性参数沿埋深 $z$ 的均值函数, $ω (z)$ 为随机波动分量函数,通常为均值 $μ_{ω} = 0$ ,标准差为 $σ_{ω}$ 的正态平稳随机场。

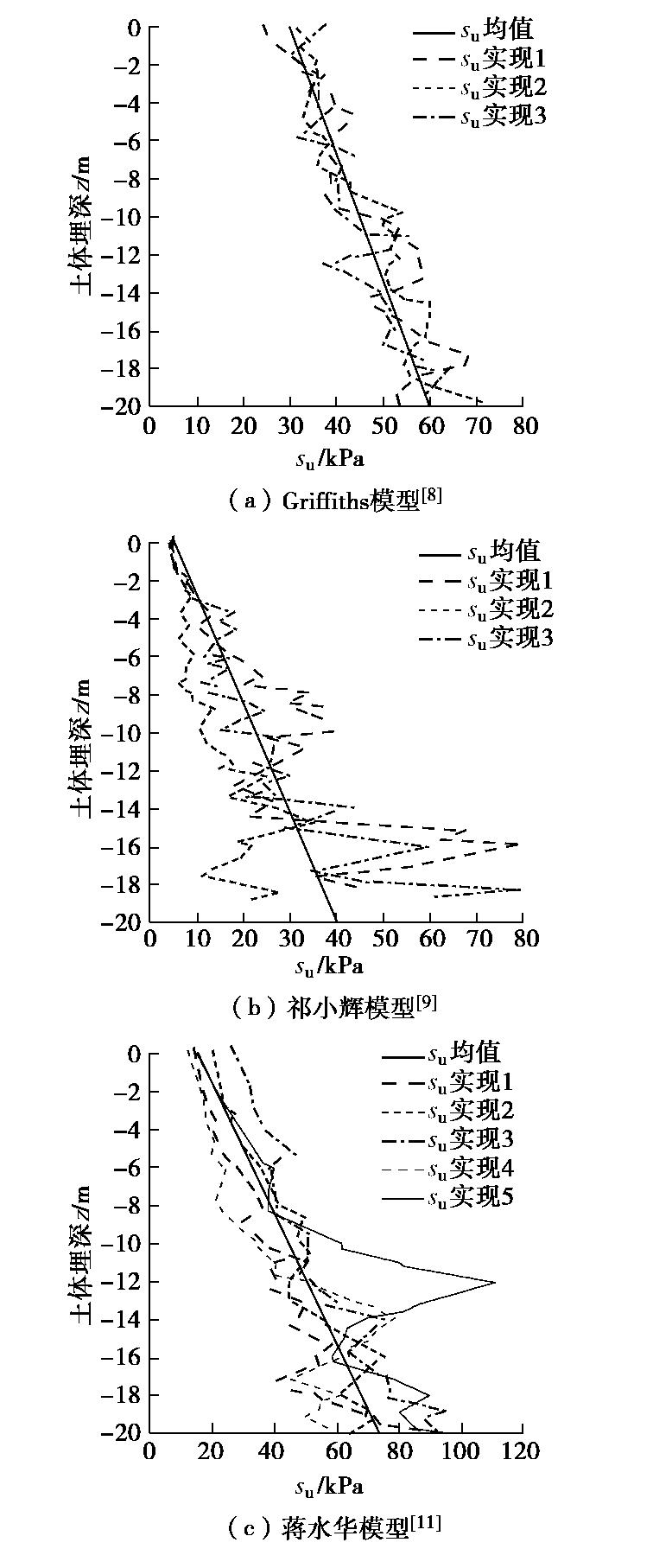
土的不排水抗剪强度 $s_{u}$ 可以看作是地表处的不排水抗剪强度 $s_{u 0}$ 随埋深线性增加^[15],即

$s_{u} (z) = s_{u 0} + b {σ^{'}}_{v} = s_{u 0} + b γ z$ ,

(2)

式中, $s_{u 0}$ 对应特定场地的地表抗剪强度,为常数, $b$ 为不排水抗剪强度随埋深增加的速率, ${σ^{'}}_{v}$ 为垂直有效应力, ${σ^{'}}_{v} = γ z$ , $γ$ 为土体重度,为常数。

为模拟不排水抗剪强度的非平稳特征,Griffiths等^[8]采用去趋势分析方法将 $s_{u 0}$ 模拟为均值为 $μ_{s_{u0}}$ 和标准差为 $σ_{s_{u0}}$ 的对数正态平稳随机场,得到如下 $s_{u}$ 的非平稳随机场：

$s_{u} (z) = s_{u 0} (z) + \frac{s_{u0} (z)}{μ_{s_{u 0}}} \cdot b γ z$ 。

(3)

则 $s_{u}$ 的均值和标准差分别为

$\begin{array}{l} μ_{s_{u}} (z) = μ_{s_{u 0}} + b γ z, \\ σ_{s_{u}} (z) = \frac{μ_{s_{u 0}} + b γ z}{μ_{s_{u 0}}} \cdot σ_{s_{u 0}} 。 \end{array}}$

(4)

式中, $s_{u}$ 的均值和标准差均为埋深的单调增加函数。

祁小辉等^[9]将参数 $b$ 模拟为均值为 $μ_{b}$ 和标准差为 $σ_{b}$ 的对数正态平稳随机场,得到 $s_{u}$ 的非平稳随机场模型：

$s_{u} (z) = s_{u 0} + γ z b (z)$ ,

(5)

则 $s_{u}$ 的均值和标准差分别为

$\begin{array}{l} μ_{s_{u}} (z) = s_{u 0} + γ z μ_{b}, \\ σ_{s_{u}} (z) = γ z σ_{b} 。 \end{array}}$

(6)

该模型中, $s_{u}$ 的均值和标准差也随深度单调增加。

蒋水华等^[11]在上述研究的基础上分别考虑了不排水抗剪强度的趋势分量和随机波动分量的不确定性,将 $s_{u 0}$ 和 $b$ 分别模拟为对数正态随机变量ln ( $μ_{s_{u 0}}$ , $σ_{s_{u 0}}$ )和ln( $μ_{b}$ , $σ_{b}$ ),并引入零均值平稳正态随机分量 $ω (x, z)$ 表示水平向x和竖向z的其他随机涨落,从而得到 $s_{u}$ 的二维非平稳随机场：

$s_{u} (x, z) = s_{u 0} + b γ z \exp [ω (x, z)]$ ,

(7)

则 $s_{u}$ 的均值和标准差分别为

$\begin{array}{l} μ_{s_{u}} (z) = μ_{s_{u 0}} + γ z μ_{b}, \\ σ_{s_{u}} (z) = \sqrt{σ_{s_{u 0}}^{2} + γ^{2} z^{2} {(μ_{b}^{2} + σ_{b}^{2}) [\exp (σ_{ω}^{2}) - 1] + σ_{b}^{2}}} 。 \end{array}}$

(8)

图2给出了分别采用Griffiths模型、祁小辉模型和蒋水华模型得到的不排水抗剪强度的若干典型实现。与Griffiths模型及祁小辉模型相比,蒋水华模型由于在趋势项基础上进一步叠加了随机涨落分量,其不排水抗剪强度沿埋深表现出更为显著的非平稳性,个别样本沿深度方向表现出剧烈变化。但总体而言,以上3种模型所描述的土性参数均值和标准差均随深度连续变化,其中均值随深度线性增大。这与由同类土壤构成的单一土层的特性是相符的^[14-17]。

图 2

$s_{u}$ 随机场沿土体埋深方向的典型实现

Figure 2. Typical realizations of random field of undrained shear strength with depth

下载: 全尺寸图片幻灯片

然而,对于规模较大的边坡工程,通常沿深度方向由不同类别的土壤构成,表现出显著的分层特性。由王长虹等^[3]对天津地铁^#5、^#6线环湖西路站—宾馆西路站四线隧道交叠区间、深度为36 m的断面黏聚力和内摩擦角参数所作调查统计结果表明,其黏聚力均值 $μ_{c}$ 与内摩擦角均值 $μ_{φ}$ 随深度方向呈非连续的阶梯状变化。土性参数的统计特征参数的这一非连续性变化,如抗剪强度参数均值、方差沿埋深的突然降低或增强,会导致临界滑移面的改变,对边坡稳定可靠性、地基承载力可靠性等会造成较大影响。可见,对于尺度较大的由不同类别土壤构成的土体,上述均值连续线性变化的非平稳随机场模型不再适用,而需建立更为合理的非平稳随机场模型。

针对土性参数的复杂空间变异性,Wei等^[18-19]提出了不精确随机模拟法,认为统计特征参数也具有不确定性,称其为模型不确定性^[20],并将统计特征参数也视为随机变量。这类模型较为复杂,其随机场离散难度与计算量都大大增加。Phoon等^[21]则假设局部场地与较大范围（如全球范围的同类或相似土壤）的土性参数空间变异性相近,基于贝叶斯机器学习提出了利用较大空间区域的参数预测并补足局部场地参数缺失值的方法。该方法是由大空间范围的数据而非通过建立特定场地的参数非平稳随机场模型来模拟局部场地数据,其预测或补充参数的合理性依赖于给定边坡或土层与其他已知区域空间变异性的相似性,对于由多种土壤构成的边坡其适用性与合理性还有待验证。

2. 统计参数非连续变化的分层非平稳随机场

对于深度较大的土体,沿深度方向可能由多种类别土壤构成,具有明显的分层特性,土性参数均值与方差等随土体深度呈非连续变化。而对于尺度较小的土体,虽然可近似视为由单一类别土壤构成,但若存在局部薄弱层,也会造成土性参数均值和方差的非连续变化,以下针对土体的这一分层特性,提出土性参数的分层非平稳随机场模型。

2.1 分层非平稳随机场模型

在此主要考虑土性参数沿深度方向的变异性。设土性参数 $ζ$ 的非平稳随机场模型为

$ζ (z) = μ_{ζ} (z) + b (z) \cdot z \cdot \exp [ω (z)]$ ,

(9)

式中, $ζ （ z)$ 可为黏聚力、内摩擦角、重度、渗透率等土性参数, $μ_{ζ} (z)$ 为土性参数的均值函数, $ω (z)$ 为零均值、标准差为 $σ_{ω} (z)$ 的土性参数非平稳随机场,表示参数方差随深度的变异性, $b (z)$ 为随机涨落分量。

针对前述土体的分层特性,可设在由同类土构成的同一土层内,土性参数为均值和方差随深度线性增加的非平稳随机场,即在同一层土体内, $b (z)$ 为均值为 $μ_{b_{I}}$ 、标准差为 $σ_{b_{I}}$ 的平稳随机场,对不同土层其均值与标准差不同,则有

$\begin{array}{l} μ_{ζ_{I}} (z) = μ_{ζ_{I 0}} + μ_{b_{I}} \cdot z, \\ σ_{ζ_{I}} (z) = z \cdot \sqrt{(μ_{b_{I}}^{2} + σ_{b_{I}}^{2}) [\exp (σ_{ω_{I}}^{2}) - 1] + σ_{b_{I}}^{2}} 。 \end{array}}$

(10)

式中,下标I对应第I个土层, $μ_{ζ_{I 0}}$ 为第I个土层土性参数的参考均值。 $l_{I - 1} \leq z < l_{I}$ , $Δ l_{I} = | l_{I} - l_{I - 1} |$ （ $I = 1 \sim N$ ）为第I层的土层厚度,可由经验或各层土的相关函数决定。

进一步地,可将上述分层非平稳随机场简化为均值与随机涨落函数沿土层跳跃变化的随机方波过程,即同一土层的土性参数为平稳随机场,其均值和方差不随深度变化, $b (z)$ 为零均值、标准差为 $σ_{b_{I}}$ 的平稳随机场,则式（10）可简化为

$ζ (z) = μ_{ζ} (z) + b (z) \times z$ 。

(11)

土性参数沿深度方向的均值和方差均为分段取值的常数：

${\begin{cases} μ_{ζ} (z) = μ_{ζ_{I 0}}, \\ σ_{ζ} (z) = σ_{ζ_{I}} = σ_{b_{I}} 。 \end{cases}$

(12)

如此建立的分层非平稳随机场模型如图3所示。

图 3 土性参数的统计特征参数随埋深的变化

Figure 3. Variation of statistical characteristic parameters of soil parameters with depth

下载: 全尺寸图片幻灯片

2.2 分层非平稳随机场的离散

根据式（11）,（12）可建立分层非平稳随机场沿深度方向的协方差矩阵。根据Bergado等^[22]和Li等^[23]的研究,边坡稳定可靠性对自相关函数的形式不敏感,而对相关长度敏感,故采用形式较为简单的指数衰减型相关函数,并根据式（10）对其进行修正,得到同一土层中任意两点i,j的协方差 $B_{i j}$ 为

$B_{i j} = σ (z_{i}) \cdot σ (z_{j}) \cdot \exp (- \frac{2 | z_{i} - z_{j} |}{θ})$ ,

(13)

式中, $| z_{i} - z_{j} |$ 是i,j两点之间的距离, $σ (z_{i})$ 和 $σ (z_{j})$ 分别是其标准差, $θ$ 是该点所在土层的相关长度。由N层土壤构成的土体分层非平稳协方差矩阵为

$B = [\begin{array}{l} \begin{matrix} B_{11} & B_{12} & \dots & \begin{matrix} B_{1 I} & \begin{matrix} \dots & B_{1 N} \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} B_{22} & \dots & \begin{matrix} B_{2 I} & \begin{matrix} \dots & B_{2 N} \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} ⋱ & \begin{matrix} \begin{matrix} ⋮ \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} B_{I I} & \begin{matrix} B_{I J} & \begin{matrix} \dots & B_{I N} \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} 对称 & \begin{matrix} ⋱ & \begin{matrix} ⋮ \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} \begin{matrix} \begin{matrix} B_{N N} \end{matrix} \end{matrix} \end{matrix} \end{array}] (I, J = 1 \sim N)$ 。

(14)

协方差矩阵 $B$ 为正定矩阵,不同层之间协方差为零,即 $B_{I J} = 0 (I \neq J)$ 。对其进行Cholesky分解,有

$B = L \times L_{}^{T}$ ,

(15)

式中, $L$ 为下三角矩阵, $L_{I J} =$ 0（I<J）。当 $I = J$ 时,记作 $B_{I J} = B_{I}$ , $L_{I J} = L_{I}$ 。

将式（15）代入式（11）,可得土性参数的分层非平稳随机场模型为

$ζ_{I} (z) = L_{I} \times ε + μ_{ζ_{I}} (z) + b_{I} (z) \times z$ ,

(16)

式中, $ε$ 为向量, $ε = {〈 ε_{1}, ε_{2}, \dots, ε_{k}, \dots, ε_{n} 〉}^{T}$ , $ε_{k}$ 为服从标准正态分布的随机变量。

上述土性参数分层非平稳随机场模拟方法的步骤如下：

（1）根据边坡剖面图,沿深度方向将边坡分为N层,通过连续回归分析确定各层土性参数的统计特征,包括均值、方差、分布类型、自相关函数或相关长度等。

（2）依照方差结构,建立第I个土层的非平稳协方差矩阵 $B_{I}$ ,见式（13）,（14）。

（3）利用Cholesky分解技术,对非平稳协方差矩阵进行分解,见式（15）,得到下三角矩阵 $L_{I}$ 。

（4）利用常用的平稳随机场模拟方法得到 $b_{I}$ 。

（5）引入向量 $ε$ ,从而得到第I层随机场模型 $ζ_{I} (z) = L_{I} \times ε + μ_{ζ_{I}} (z) + b_{I} (z) \times z$ ,见式（16）。

（6）重复步骤（2）～（5）,得到分层非平稳随机场 $ζ (z) = L \times ε + μ_{ζ} (z) + b (z) \times z$ 。

本文采用K-L方法^[24]对平稳随机场进行离散。具体应用时,分层厚度可根据检测数据结合工程经验确定,或根据检测数据的相关性分析确定。如由土性参数沿深度方向的方差函数 $γ (T)$ 或相关函数 $ρ (τ)$ ^[25],可得到土性参数涨落尺度 $θ$ ：

$\begin{matrix} θ = \lim_{T \to \infty} T γ (T) \\ = 2 \lim_{T \to \infty} \int_{0}^{T} (1 - \frac{τ}{T}) ρ (τ) d τ = 2 \int_{0}^{\infty} ρ (τ) d τ 。 \end{matrix}$

(17)

其中,当两点之间距离大于涨落尺度时,可认为参数不相关,属于不同土层。据此,可近似确定同类土的土层厚度。工程上,通常也近似取相关函数值衰减到 $e^{- 1}$ 时的值,作为涨落尺度的近似。

考察分层厚度与该所在位置处的相关长度之间的相对误差是否满足收敛准则,若不满足,则改变分层厚度,直至满足为止。

$\lim_{I} \frac{| θ_{I} - Δ l_{I} |}{Δ l_{I}} \leq ε$ ,

(18)

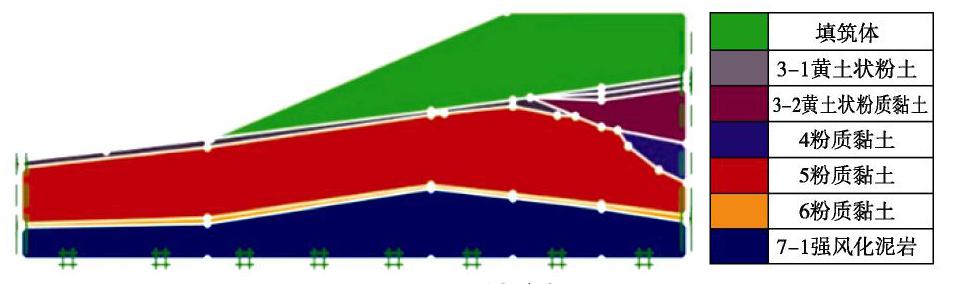
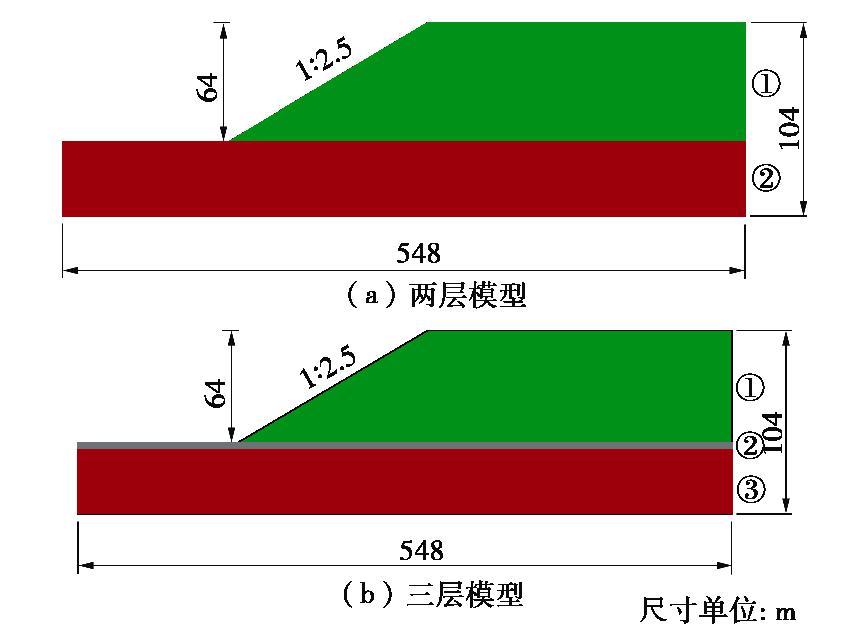
式中, $θ_{I}$ 为某深度处土性参数的相关长度。

图4为某湿陷性黄土高填方边坡剖面,坡高64 m,坡度为1∶2.5,边坡土体的分类情况列于图4。表1列出了各类土对应的土性参数平均值。根据表1中的数据,参照场地等级规范,该边坡上部土体可视为同一土层,分别建立两种分层模型,其一是忽略较薄的软弱层,将边坡划分为两层,上层为填筑土,厚度64 m,下层为粉质黏土,厚度40 m；其二是考虑软弱夹层,将边坡划分为三层,上层为填筑土,厚度64 m,中层为黄土状粉土,厚度3 m,下层为粉质黏土,厚度37 m,边坡分层模型如图5所示。该简化模型忽略了土层倾角的变化,并将相似土层视为同类土。前者简化可能会造成对临界滑移面预测的误差,而后者的差异可通过引入同类土的空间变异性予以考虑。

图 4 土体剖面

Figure 4. Profile of soil slope

下载: 全尺寸图片幻灯片

表 1 边坡的基本土性参数

Table 1. Key soil parameters of soil slope

土类	c/kPa	φ/(°)	γ/(kN·m^-3)	E/MPa
填筑体	40	20	19.0	6.0
3-1	18	22	14.7	1.8
3-2	26	23	19.2	7.3
4	28	22	19.7	7.8
5	29	20	20.5	8.2
6	31	22	20.9	8.5
7-1	80	23	—	25.0

下载: 导出CSV

| 显示表格

图 5 简化土坡剖面

Figure 5. Simplified profile of soil slope

下载: 全尺寸图片幻灯片

采用K-L方法^[24]进行随机场离散。表2列出了针对图4边坡采用不同随机场模型的土性参数随机场模型的相关统计特征参数,其中,黏聚力、内摩擦角以及土体重度的相关参数取自Phoon等^[17]。

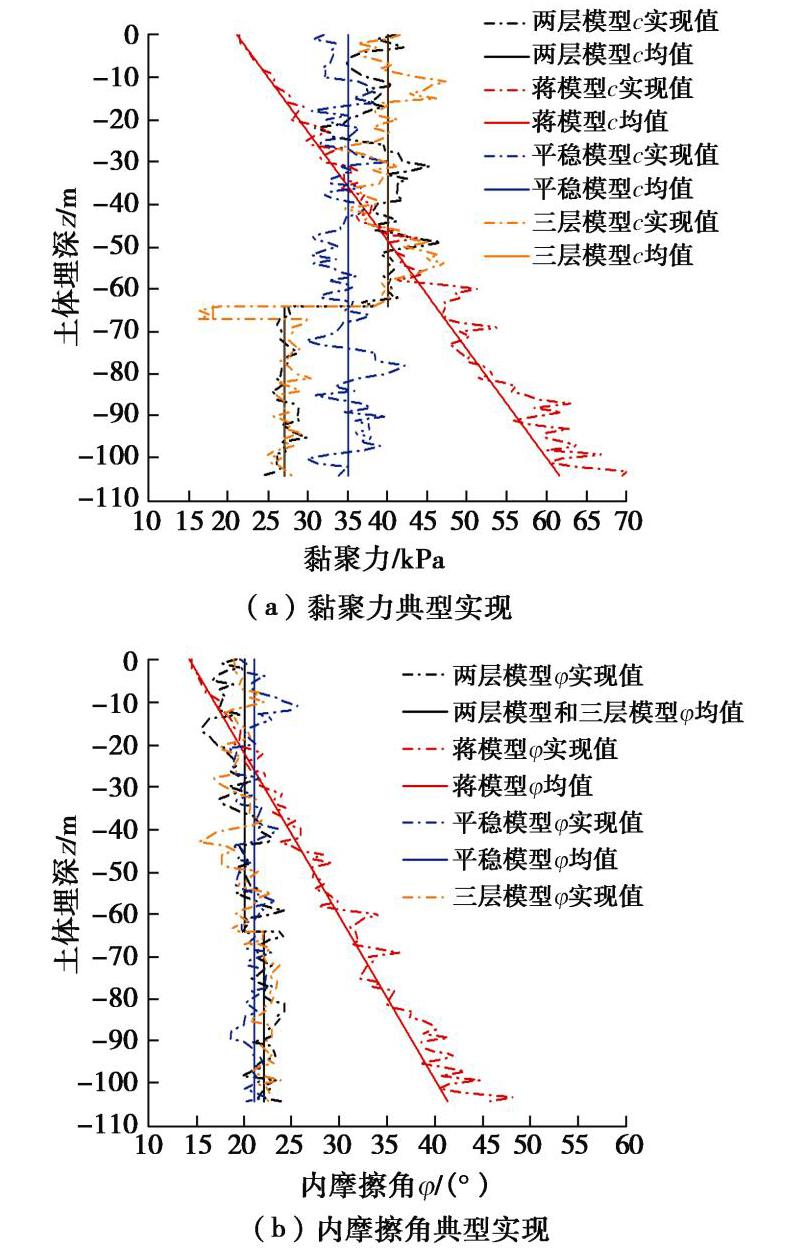
表 2 土性参数随机场模型相关参数

Table 2. Soil parameters of random field model

随机场模型	土性参数	μ	COV	l_h/m	l_v/m
平稳模型	γ/(kN·m^-3)	18.4	0.18	40	6
	c/kPa	35	0.24	40	4
	φ/(°)	21	0.22	40	4
蒋水华非平稳模型	γ/(kN·m^-3)	18.4	—	—	—
	c/kPa	35	0.24	40	4
	φ/(°)	21	0.22	40	4
两层非平稳模型	γ₁/(kN·m^-3)	18.1	0.16	40	6
	c₁/kPa	40	0.30	40	10
	φ₁/(°)	20	0.30	40	10
	γ₂/(kN·m^-3)	19	0.21	40	6
	c₂/kPa	27	0.22	40	4
	φ₂/(°)	22	0.19	40	4
三层非平稳模型	γ₁/(kN·m^-3)	18.1	0.16	40	6
	c₁/kPa	40	0.30	40	10
	φ₁/(°)	20	0.30	40	10
	γ₂/(kN·m^-3)	14.7	0.14	40	6
	c₂/kPa	18	0.30	40	4
	φ₂/(°)	22	0.21	40	4
	γ₃/(kN·m^-3)	19	0.21	40	6
	c₃/kPa	27	0.22	40	4
	φ₃/(°)	22	0.19	40	4

下载: 导出CSV

| 显示表格

采用本文所提出的分层非平稳随机场,建立了抗剪强度参数黏聚力和内摩擦角随机场,其典型实现如图6所示。考虑到蒋水华模型^[11]同时考虑了均值和方差函数随深度的变化,选取该模型作为对比,图6还给出了平稳随机场模型下黏聚力 $c$ 和内摩擦角 $φ$ 的实现值。

图 6 不排水抗剪强度参数

$c$ ,

$φ$ 值沿埋深的典型实现

Figure 6. Typical simulated samples of undrained shear strength parameters with depth

下载: 全尺寸图片幻灯片

从图6可以看出,根据本文所建立分层非平稳随机场模型,所得黏聚力与内摩擦角均值沿土体埋深非连续变化,呈现明显的非平稳特征,与实际边坡剖面土性参数的分布特点一致。采用蒋水华模型所得黏聚力和内摩擦角的均值则随深度线性连续增大,其随机场实现值在均值两侧较均匀随机波动,能够较好描述土性参数的非平稳特征,但不能有效描述其分层特性。而采用平稳随机场模型得到的黏聚力和内摩擦角的均值随埋深不变,其随机场实现值在均值两侧波动,不能体现土性参数的非平稳分布特征。由此可见,对于由不同类别土壤构成的土质边坡,由于土性参数的统计特征参数具有显著非连续变化的非平稳特征,分层非平稳随机场对此可以有效描述,而均值连续线性变化的非平稳随机场模型对此阶跃式非连续变化特性的描述欠完备。

3. 边坡稳定可靠性分析与讨论

根据表2的土性参数统计值,针对图5所示简化边坡模型,分别建立平稳随机场模型、连续非平稳随机场模型^[11]以及本文提出的分层非平稳随机场模型,并利用有限元极限分析方法（finite element limit analysis,简记为FELA）,进行边坡稳定可靠度计算。

3.1 边坡稳定可靠性分析方法

FELA基于塑性极限分析理论,结合广义变分原理与混合有限元方法,通过建立静力许可应力场和运动许可速度场,用线性规划算法,从而求解破坏荷载（或极限承载力）下限与上限的一种数值分析方法^[26-28]。FELA能快速得到问题的严格上下限以及可能的临界滑移面^[13]。

假设土为理想弹塑性材料,比例加载,土质边坡稳定性问题的广义变分原理可写为

$\begin{matrix} \min_{\dot{u}} \max_{σ, α} α + \int_{V} σ^{T} \nabla \dot{u} d v - \int_{V} f^{T} \dot{u} d v - \int_{S} (α t_{ext} + t_{s})^{T} \dot{u} d s \\ s .t . F (σ) \leq 0 \end{matrix}$ 。

(19)

式中 $α$ 为荷载因子； $σ$ 为边坡内任一点应力状态； $f$ 为边坡内体积力矢量,通常为重力矢量； $\dot{u}$ 为边坡速度矢； $t_{ext}$ 为边坡外荷载矢量,对于边坡失稳问题,通常只考虑重力作用,该项为零； $t_{s}$ 为孔隙压力, $F (σ)$ 为理想弹塑性材料屈服函数,可采用多面体近似将其转化为线性约束：

$f_{i} σ - k_{i} \leq 0 (i = 1 ~ n)$ ,

(20)

式中, $f_{i}, k_{i}$ 为对应的分段线性化屈服函数。

将上述有限元极限分析理论,结合强度折减法,对边坡进行稳定性分析,边坡安全系数为

$F_{s} = \frac{土体抗剪强度}{极限平衡状态剪应力} = \frac{\tan φ}{\tan φ_{cr}} = \frac{c}{c_{cr}}$ 。

(21)

由于土性参数的空间变异性,导致边坡安全系数不再为常数,而是随机变量。采用Monte Carlo法结合FELA法进行边坡稳定可靠性分析^[29]。边坡失效概率 $P_{f}$ 为

$P_{f} = P [g (X) \leq 0] = P [F_{s} - 1 \leq 0] = \int_{F_{s} \leq 1} f (F_{s}) d F_{s}$ ,

(22)

式中, $f (F_{s})$ 为边坡安全系数的概率密度函数, $X =$ ${x_{1}, x_{2}, \dots, x_{n}}^{T}$ 为参数随机场。

3.2 边坡安全系数分布特点

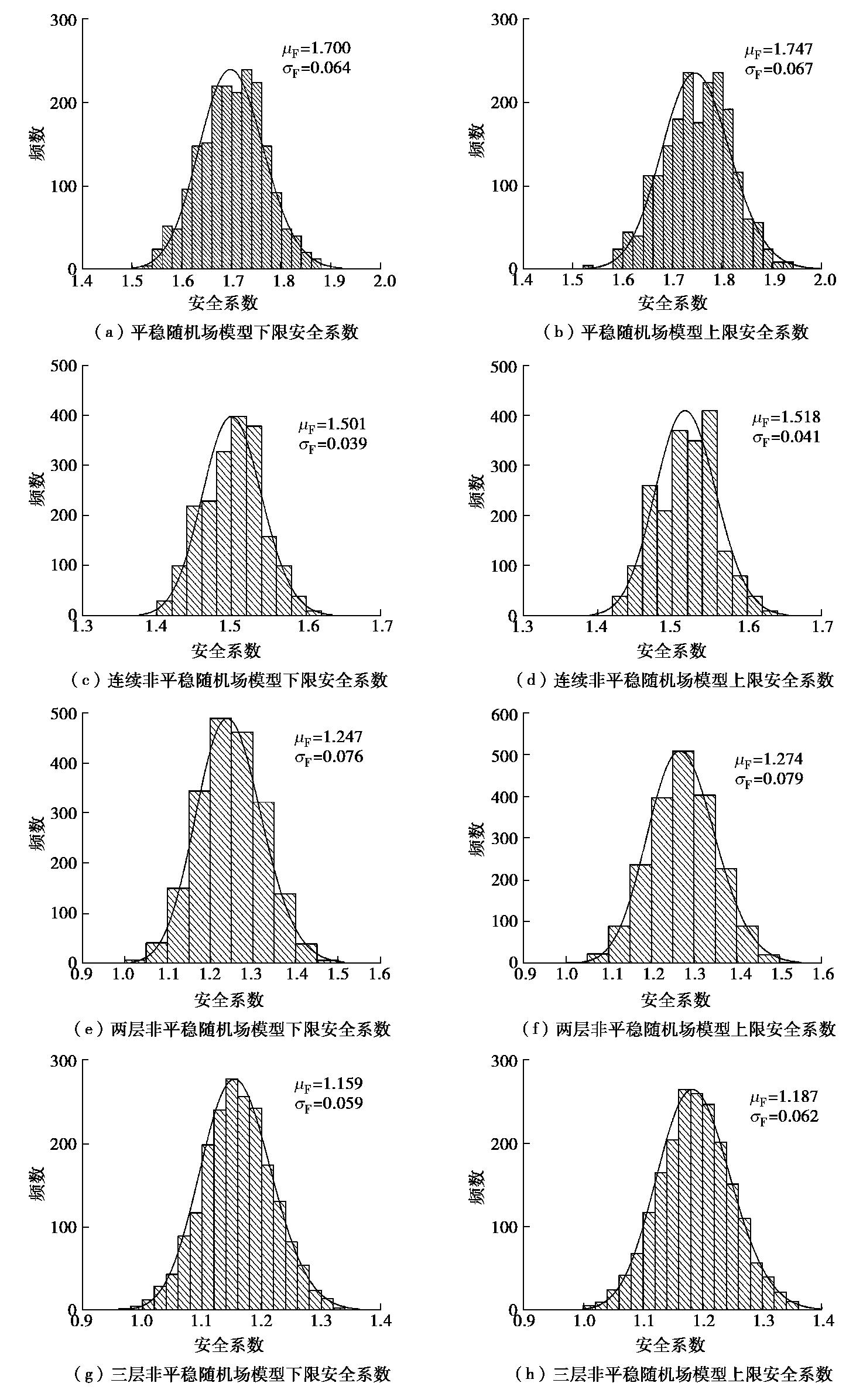
采用Monte Carlo法模拟2000次,各参数随机场模型所得的边坡安全系数分布如图7所示。

图 7 各模型的边坡稳定安全系数分布规律

Figure 7. Distribution of safety factor of soil slope

下载: 全尺寸图片幻灯片

经检验,各模型边坡安全系数分布均服从对数正态分布。采用平稳随机场模型时,如图7（a）,（b）所示,安全系数上下限均值分别为1.747,1.700,为各种模型中最大者；其次为连续非平稳随机场模型结果,如图7（c）,（d）所示,安全系数上下限均值分别是1.518,1.501,均小于平稳随机场分析值；采用两层非平稳随机场,如图7（e）,（f）所示,安全系数上下限均值分别为1.274,1.247；3层非平稳随机场模型（图7（g）,（h））,安全系数上下限均值分别为1.187,1.159。3层非平稳模型由于明确考虑了软弱层的影响,安全系数的上下限均值是各种模型中最小者。上述4种模型中,参数线性连续变化非平稳随机场模型的安全系数分布图较其他模型尖窄,由图8所示各模型典型临界滑移面可知,这可能是由于该随机场模型给出的滑移模式较为集中所致。上述安全系数的差异表明,平稳随机场模型由于忽略了参数的非平稳特性,会高估边坡失稳风险。

图 8 抗剪强度参数云图和边坡临界滑移面

Figure 8. Nephogram of shear strength parameters and critical slip surface of soil slope

下载: 全尺寸图片幻灯片

3.3 各模型滑坡模式比较

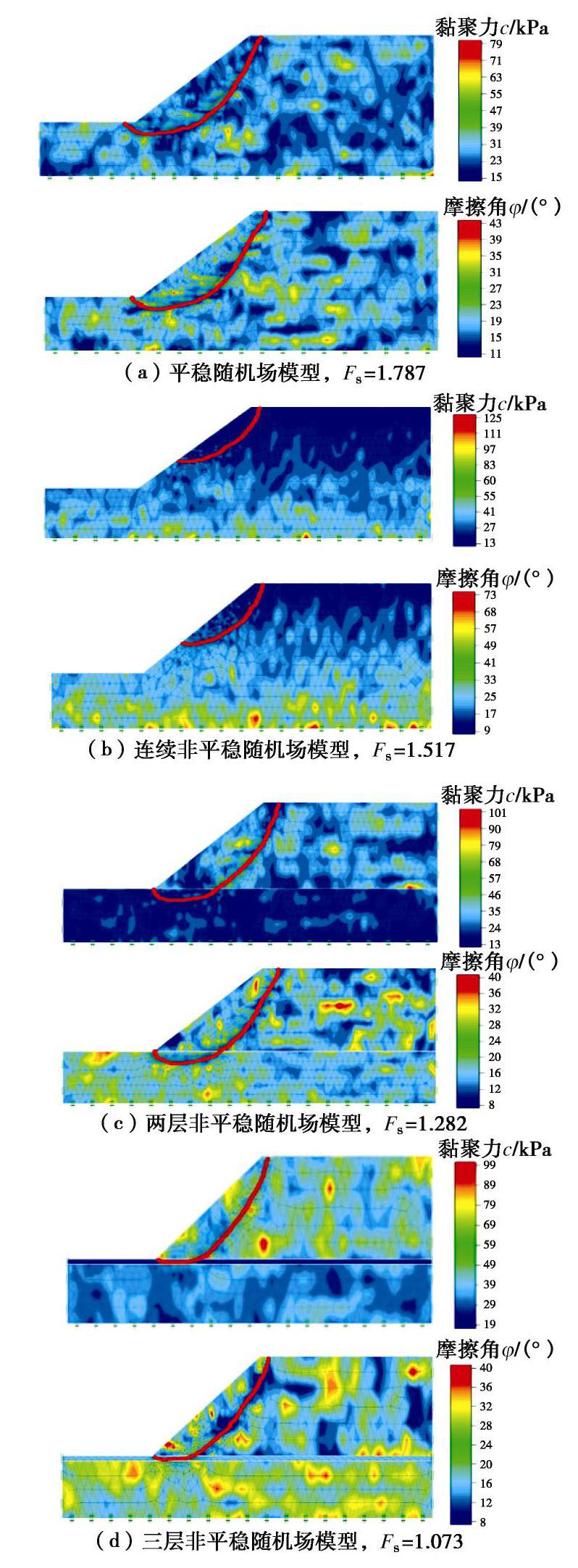
进一步对比采用不同参数随机场模型所得到的边坡临界滑移面的形状和位置差异。图8选取了4种随机场模型的典型边坡临界滑移面及其相应的抗剪强度参数c,φ样本云图。平稳随机场模型,由于忽略统计特征参数的空间变异性,可以得到位于坡面或坡脚的浅层或深层滑移模式,其中,与安全系数均值区域对应的典型滑移模式主要为滑移面下凹、剪出口位于坡底的深层滑坡,如图8（a）所示；采用蒋水华等提出的线性连续非平稳随机场模型,该模型虽然可以生成抗剪强度参数急剧变化的个别样本（图2（c））,但由于黏聚力与内摩擦角的均值函数总体沿埋深线性连续增大,因此,所得到的边坡失效模式主要为沿坡面的浅层失稳模式,滑坡剪出口位于上部坡面,未穿过薄弱层,如图8（b）所示；两层非平稳随机场,滑移面处于相对较弱的下层土中,其滑坡剪出口位于坡脚,滑移面形状与平稳随机场模型类似,如图8（c）所示；三层非平稳随机场的边坡失效模式为处于软弱夹层中,滑坡剪出口位于坡脚,滑移面形状也与平稳随机场模型类似,如图8（d）所示,这与实际工程经验较为吻合。而平稳随机场模型以及线性连续非平稳随机场模型,所给出的位于边坡顶部的浅层滑移模式均与实际不符。综上,对于由多种类别土壤构成的具有分层特性的边坡,土性参数统计特征参数沿深度的非连续变化对边坡失效模式以及边坡安全系数均有显著影响,参数随机场模型应合理,并有效考虑这一非连续非平稳特性。

4. 结论

本文针对由多种类别土壤构成的具有分层特性的边坡,提出并建立了土性参数分层非平稳随机场模型,采用有限元极限分析方法,进行了边坡稳定可靠性分析,通过不同随机场模型下边坡稳定可靠性计算结果的对比分析,研究了黏聚力和内摩擦角的非均匀涨落特征对边坡稳定可靠度的影响。主要结论如下：

（1）对于具有明显分层特征的土质边坡,与平稳随机场模型以及均值线性连续变化的非平稳随机场模型相比,本文提出的分层非平稳随机场模型能有效考虑土性参数的统计特征参数随埋深非连续变化,为合理表征分层边坡土性参数的非平稳特性提供了一条有效途径。

（2）土性参数的空间变异性导致边坡存在多种失效模式,不同的抗剪强度参数随机场模型会导致对边坡临界滑移面的形状和位置的估计的显著差异。平稳随机场模型,由于忽略统计特征参数的空间变异性,所得到典型滑移模式主要为滑移面下凹、剪出口位于坡底的深层滑坡；采用线性连续非平稳随机场模型,由于黏聚力与内摩擦角的均值函数沿埋深线性连续增大,所得到的边坡失效模式均为沿坡面的浅层失稳模式,滑坡剪出口位于上部坡面,未穿过薄弱层。本文提出的分层非平稳随机场模型,明确考虑了软弱层,给出的边坡临界滑移面处于相对较弱的土层或软弱夹层中,与工程经验较为吻合。

（3）对于由多种类别土壤构成的分层边坡工程,忽略土性参数均值与方差沿空间的变异性的平稳随机场模型,会高估边坡稳定性；与均值线性连续变化的非平稳随机场模型相比,考虑土性参数的统计特征参数沿深度非连续变化的分层非平稳随机场模型的计算结果更为合理。

图 1 倾倒变形体岩体结构统计

Figure 1. Statistics of rock mass structures of toppling slope

下载: 全尺寸图片幻灯片

图 2 试验设备与边坡物理模型

Figure 2. Geotechnical centrifuge and physical model for slope

下载: 全尺寸图片幻灯片

图 3 边坡数值模型

Figure 3. Numerical slope model of centrifugal tests

下载: 全尺寸图片幻灯片

图 4 位移曲线对比

Figure 4. Comparison of displacement curves

下载: 全尺寸图片幻灯片

图 5 典型时刻物理模型变形图

Figure 5. Deformations of physical model at typical time

下载: 全尺寸图片幻灯片

图 6 物理模型位移矢量图

Figure 6. Displacement vectors of physical model

下载: 全尺寸图片幻灯片

图 7 数值模型变形破坏图

Figure 7. Deformation and failure of numerical model

下载: 全尺寸图片幻灯片

图 8 边坡位移–速率–加速度时程曲线

Figure 8. Time-history curves of slope displacement-rate-acceleration

下载: 全尺寸图片幻灯片

图 9 点对相对位移曲线

Figure 9. Relative displacement curves of point couples

下载: 全尺寸图片幻灯片

图 10 不同倾角、坡角时的边坡破坏模式

Figure 10. Failure modes of slope at different dip and slope angles

下载: 全尺寸图片幻灯片

图 11 坡角、倾角及层面c、φ值对边坡稳定的影响

Figure 11. Effects of slope angle, dipangle, c and φ on slope stability

下载: 全尺寸图片幻灯片

表 1 相似材料最终配比

Table 1 Final ratios of similar materials

相似材料	石英砂	石膏	水泥	水	重晶石
硬岩	1	0.600	0.050	0.400	0
软岩	1	0.350	0.025	0.613	1

下载: 导出CSV

表 2 数值模型材料参数

Table 2 Material parameters of numerical model

材料	密度ρ/(kg·m^-3)	法相刚度 $\frac{k_{in}}{k_{n}} / 10^{9}$	剪切刚度 $\frac{k_{is}}{k_{s}} / 10^{9}$	黏聚力 $\frac{c_{ij}}{k_{j}} / (10^{4} Pa)$	抗拉强度 $\frac{σ_{it}}{σ_{t}} / (10^{6} Pa)$	内摩擦角 $\frac{φ_{ij}}{φ_{j}}$ /(°)	残余摩擦角φ_ijres/(°)
硬岩	2850	28	25	3.4×10²	2.5	23	18
软岩	2250	14	12	1.4×10²	1.1	15	10
层面	—	8	7.5	1.5	0	12	—

下载: 导出CSV

参考文献(23)

[1]	黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J]. 岩石力学与工程学报, 2007, 26(3): 433-454. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200703000.htm HUANG Run-qiu. Large-scale landslides and their sliding mechanisms in china since the 20th century[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 433-454. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200703000.htm
[2]	黄润秋, 李渝生, 严明. 斜坡倾倒变形的工程地质分析[J]. 工程地质学报, 2017, 25(5): 1165-1181. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201705001.htm HUANG Run-qiu, LI Yu-sheng, YAN Ming. The implication and evaluation of toppling failure in engineering geology practice[J]. Journal of Engineering Geology, 2017, 25(5): 1165-1181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201705001.htm
[3]	谭儒蛟, 杨旭朝, 胡瑞林. 反倾岩体边坡变形机制与稳定性评价研究综述[J]. 岩土力学, 2009, 30(增刊2): 479-484, 523. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2009S2104.htm TAN Ru-jiao, YANG Xu-zhao, HU Rui-lin. Review of deformation mechanism and stability analysis of anti-dipped rock slopes[J]. Rock and Soil Mechanics, 2009, 30(S2): 479-484, 523. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2009S2104.htm
[4]	陈孝兵, 李渝生, 赵小平. 底摩擦重力试验在倾倒变形岩体稳定性研究中的应用[J]. 地学前缘, 2008, 15(2): 300-304. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY200802038.htm CHEN Xiao-bing, LI Yu-sheng, ZHAO Xiao-ping. The application of bottom-friction gravity test to the study of the stability of the toppling rock mass[J]. Earth Science Frontiers, 2008, 15(2): 300-304. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY200802038.htm
[5]	郑达, 黄润秋, 黄刚. 地下开采作用下“反倾上硬下软”型斜坡崩塌形成机制研究——以贵州开阳磷矿崩塌为例[J]. 工程地质学报, 2014, 22(3): 464-473. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201403020.htm ZHENG Da, HUANG Run-qiu, HUANG Gang. Mechanism of rockfall with anti-dip and top hard-bottom soft rock by underground mining: a case study of rockfall in Kaiyang phosphorite, Guizhou[J]. Journal of Engineering Geology, 2014, 22(3): 464-473. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201403020.htm
[6]	包承纲. 我国岩土离心模拟技术的应用与发展[J]. 长江科学院院报, 2013, 30(11): 55-66, 71. https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB201311013.htm BAO Cheng-gang. Application and development of centrifugal modeling technology for geotechnical engineering in china[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(11): 55-66, 71. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CJKB201311013.htm
[7]	ADHIKARY D P, DYSKIN A V, JEWELL R J, et al. A study of the mechanism of flexural toppling failure of rock slopes[J]. Rock Mechanics and Rock Engineering, 1997, 30(2): 75-93.
[8]	汪小刚, 张建红, 赵毓芝, 等. 用离心模型研究岩石边坡的倾倒破坏[J]. 岩土工程学报, 1996, 18(5): 14-21. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC605.001.htm WANG Xiao-gang, ZHANG Jian-hong, ZHAO YU-zhi, et al. Investigations on mechanism of slope toppling failure by centrifuge model testing[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(5): 14-21. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC605.001.htm
[9]	吴昊, 赵维, 年廷凯, 等. 反倾层状岩质边坡倾倒破坏的离心模型试验研究[J]. 水利学报, 2018, 49(2): 223-231. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201802009.htm WU Hao, ZHAO Wei, NIAN Ting-kai, et al. Study on the anti-dip layered rock slope toppling failure based on centrifuge model test[J]. Journal of Hydraulic Engineering, 2018, 49(2): 223-231. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201802009.htm
[10]	蒋金阳. 软硬互层边坡倾倒变形破坏特征及支护效果的大型离心机试验研究[D]. 成都: 成都理工大学, 2017. JIANG Jin-yang. Experimental Study on Failure Characteristics and Support Effect of Soft and Hard Interbedded Slope Toppling Deformation in Large Scale Centrifuge: A Case Study of the Right Bank Slope of the Right Bank of the Miao Tail[D]. Chengdu: Chengdu University of Technology, 2017. (in Chinese)
[11]	ORR M C, SWINDELLS C F. Open pit toppling failures: Experience versus analysis[C]//Proceedings of the 7th International Congress on Computer Method and Advance in Geomechanics, 1991, Cairus: 505-510.
[12]	LEANDRO R A, IVÁN G, ROBERTO M. Analysis of a complex toppling-circular slope failure[J]. Engineering Geology, 2010, 114(1): 93-104.
[13]	COGGAN J S, PINE R J. Application of distinct-element modelling to assess slope stability at Delabole slate quarry[C]//Cornwall, England: Trans Inst Min Metall (Sec A: Mining Industry), 1996.
[14]	孙东亚, 彭一江, 王兴珍. DDA数值方法在岩质边坡倾倒破坏分析中的应用[J]. 岩石力学与工程学报, 2002, 21(1): 39-42. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200201007.htm SUN Dong-ya, PENG Yi-jiang, WANG Xing-zhen. Application of dda method in stability analysis of topple rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(1): 39-42. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200201007.htm
[15]	马昊, 黄达, 石林. 基于断距–层厚特征统计的反倾边坡S型破坏演化数值模拟[J/OL]. 工程地质学报: 1-11[2020-05-09]. doi: 10.13544/j.cnki.jeg.2019-042. MA Hao, HUANG Da, SHI Lin. Numerical simulation of s-shaped failure evolution of anti-dip slope based on statistics of broken length and layerthickness[J/OL]. Journal of Engineering Geology. [2020-05-09] doi: 10.13544/j.cnki.jeg.2019-042. (in Chinese)
[16]	程东幸, 刘大安, 丁恩保, 等. 层状反倾岩质边坡影响因素及反倾条件分析[J]. 岩土工程学报, 2005, 27(11): 1362-1366. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200511027.htm CHENG Dong-xing, LIU Da-an, DING En-bao, et al. Analysis on influential factors and toppling conditions of toppling rock slope[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1362-1366. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200511027.htm
[17]	赵华, 李文龙, 卫俊杰, 等. 反倾边坡倾倒变形演化过程的模型试验研究[J]. 工程地质学报, 2018, 26(3): 749-757. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201803022.htm ZHAO Hua, LI Wen-long, WEI Jun-jie, et al. Model test study on toppling deformation evolution process of counter-tilt slope[J]. Journal of Engineering Geology, 2018, 26(3): 749-757. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201803022.htm
[18]	Itasca Consulting Group Inc. UDEC (Universal Distinct Element Code), Version 6.0[M]. Minneapolis: Itasca Consulting Group Inc, 2014.
[19]	DIEDERICHS M S, KAISER P K. Stability of large excavation in laminated hard rock masses: the voussoir analogue revisited[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(1): 97-117.
[20]	ZHENG Y, CHEN C X, LIU T T, et al. Study on the mechanisms of flexural toppling failure in anti-inclined rock slopes using numerical and limit equilibrium models[J]. Engineering Geology, 2018, 237: 116-128.
[21]	CHO N, MARTIN C D, SEGO D C. A clumped particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 997-1010.
[22]	左保成, 陈从新, 刘小巍, 等. 反倾岩质边坡破坏机理模型试验研究[J]. 岩石力学与工程学报, 2005, 24(19): 107-113. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200519016.htm ZUO Bao-cheng, CHEN Cong-xin, LIU Xiao-wei, et al. Modeling experiment study on failure mechanism of counter-tilt rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 107-113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200519016.htm
[23]	李世俊, 马昌慧, 刘应明, 等. 离心模型试验与数值模拟相结合研究采空边坡渐进破坏特性[J]. 岩土力学, 2019, 40(4): 1577-1583, 1595. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201904041.htm LI Shi-jun, MA Chang-hui, LIU Ying-ming, et al. Centrifuge model tests and numerical simulation on progressive failure behavior of slope above a mine-out area[J]. Rock and Soil Mechanics, 2019, 40(4): 1577-1583, 1595. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201904041.htm

施引文献(8)

期刊类型引用(4)

1.	王体强，王永志，梁小丛，王德咏，陈卓识. 超重力模型试验干–饱和砂动剪切模量阻尼比特性研究. 岩石力学与工程学报. 2023(06): 1546-1559 . 百度学术
2.	陈平山，梁小丛，王体强，王德咏，王永志，樊旭，陈卓识，袁晓铭. 珊瑚礁砂与标准砂场地液化特征动力离心试验研究. 岩石力学与工程学报. 2023(09): 2283-2294 . 百度学术
3.	黄晓实，黄俊清，颜业敢，汪玉冰. 基于动土压力影响的坝基动剪切模量反演研究. 岩土力学. 2023(10): 2889-2898 . 百度学术
4.	王永志，王体强，袁晓铭，张雪东，陈卓识. 动力离心试验反演分析砂土模量阻尼比特征与可靠性. 岩石力学与工程学报. 2022(08): 1717-1727 . 百度学术