非一致激励下长大盾构隧道结构地震响应分析

王国波; 巴峰; 孙富学; 袁明智; 郝朋飞

doi:10.11779/CJGE202007006

非一致激励下长大盾构隧道结构地震响应分析 English Version

王国波^{1, 2,},
巴峰¹,
孙富学^2, ,,
袁明智¹,
郝朋飞¹

1.
武汉理工大学道路桥梁与结构工程湖北省重点实验室,湖北　武汉　430070
2.
温州大学建筑工程学院,浙江　温州　325035

基金项目:

国家自然科学基金项目 51878529

国家自然科学基金项目 51678465

武汉理工大学研究生优秀学位论文培育项目 2018-YS-044

详细信息

作者简介:
王国波(1979—),男,博士,教授,主要从事工程结构的抗震分析研究工作。E-mail：wgb16790604@126.com

通讯作者:
孙富学, E-mail：sunfuxue@163.com

中图分类号: TU435
计量
- 文章访问数: 315
- HTML全文浏览量: 28
- PDF下载量: 185
出版历程
- 收稿日期: 2019-10-15
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-06-30

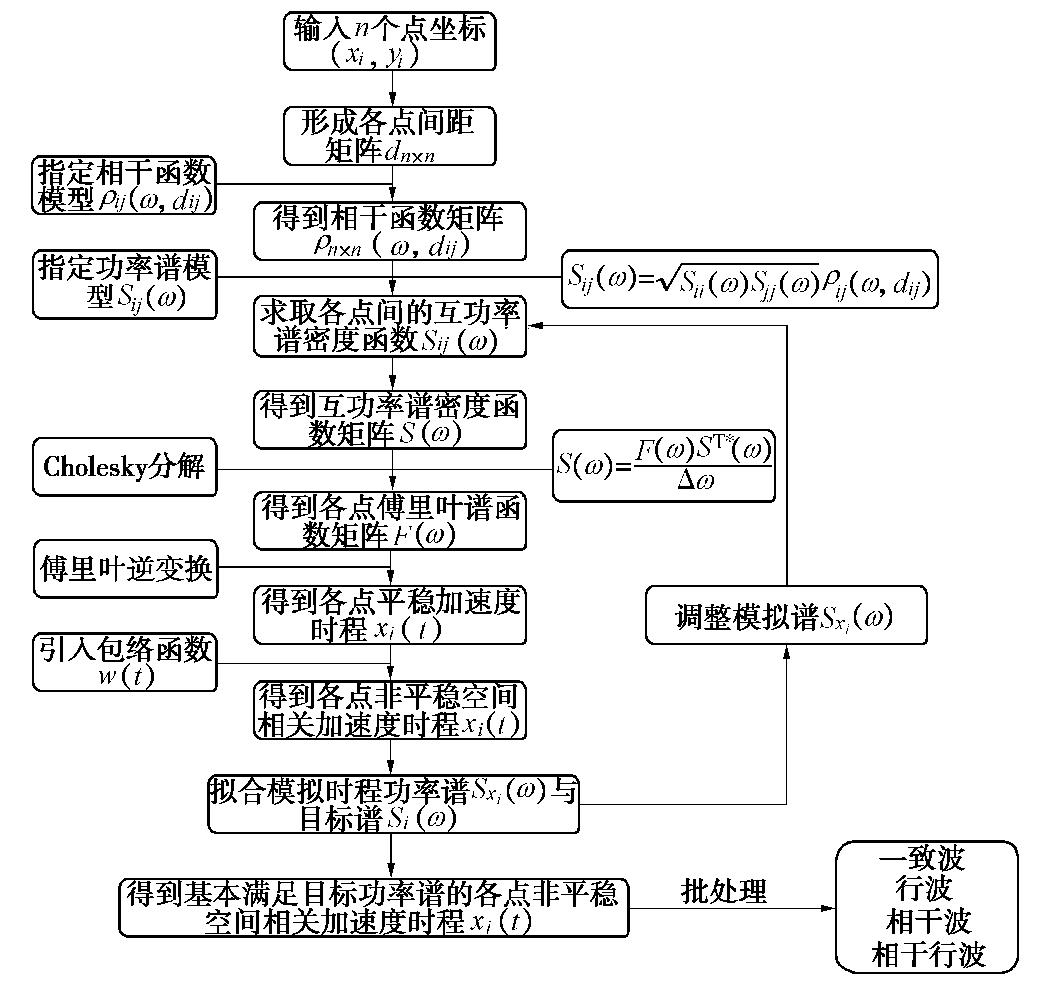
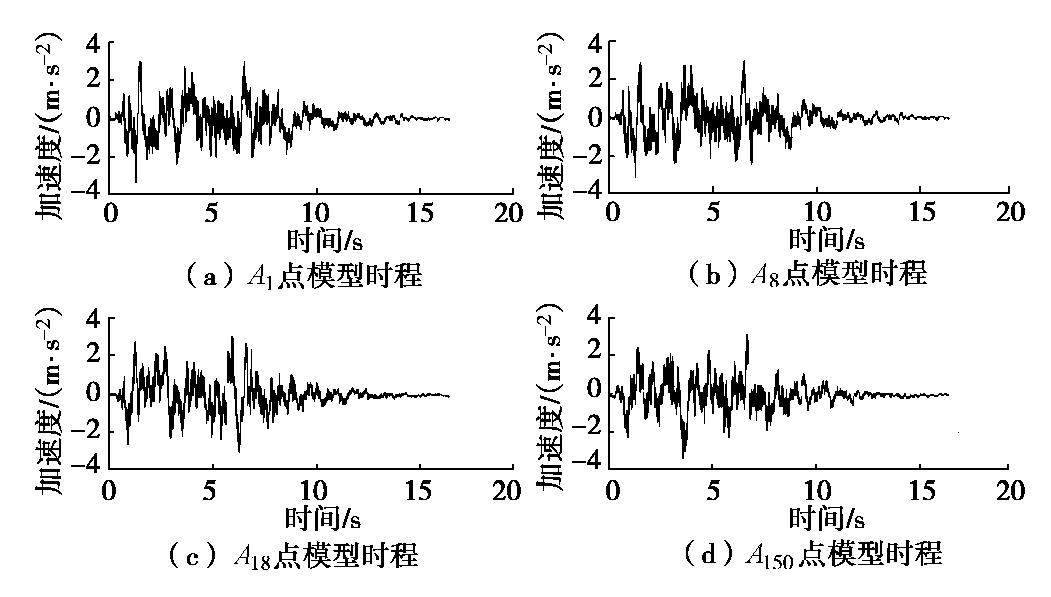
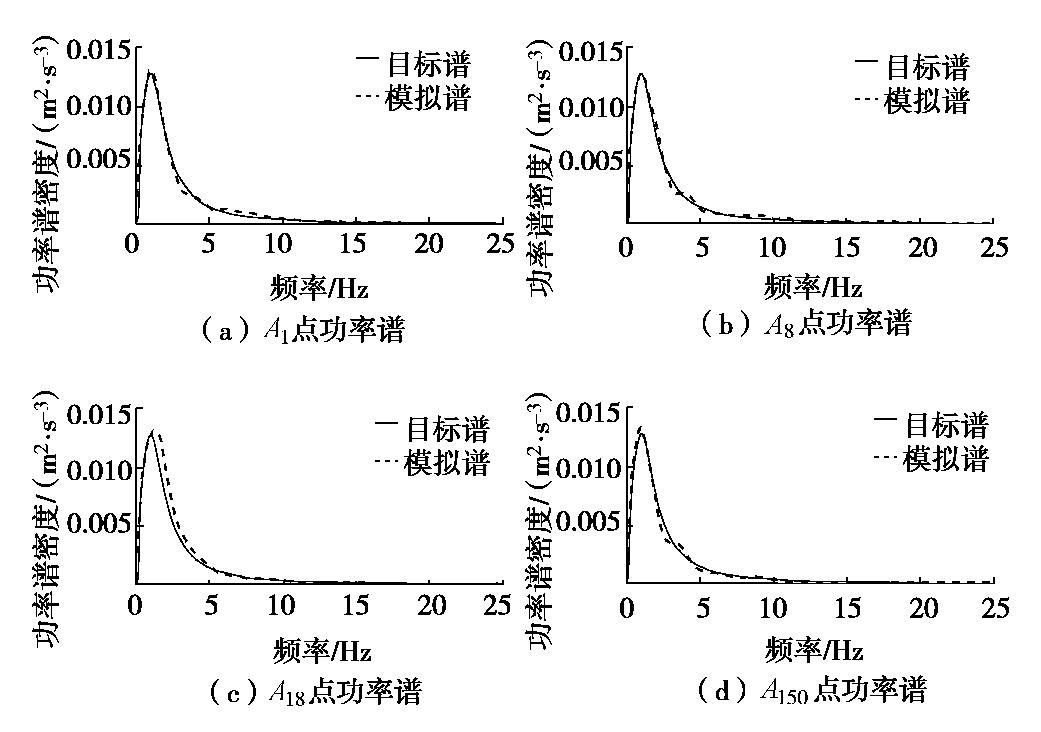
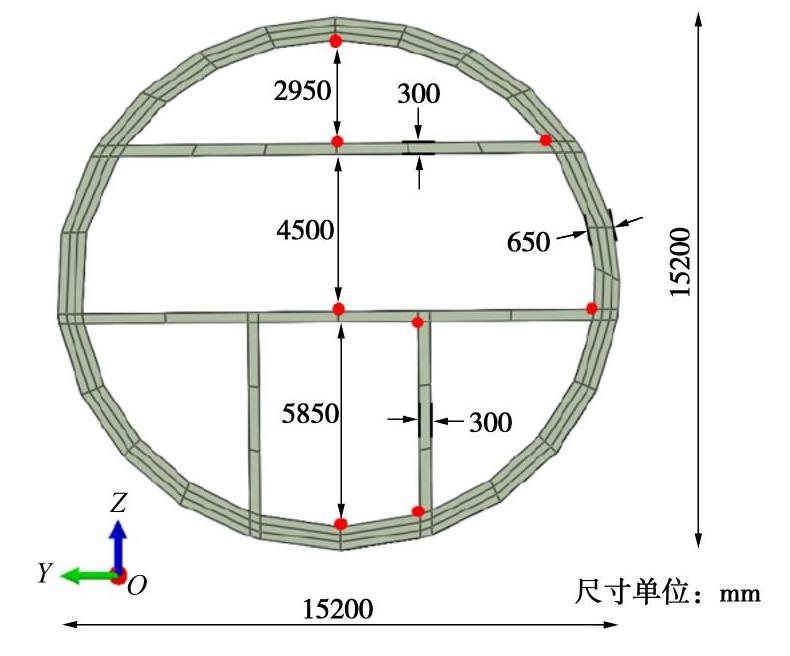
Seismic response analysis of long shield tunnels under non-uniform excitation

1.
Hubei Key Laboratory of Roadway Bridge and Structure Engineering, Wuhan University of Technology, Wuhan 430070, China
2.
College of Civil Engineering and Architecture, Wenzhou University, Wenzhou 325035, China

摘要

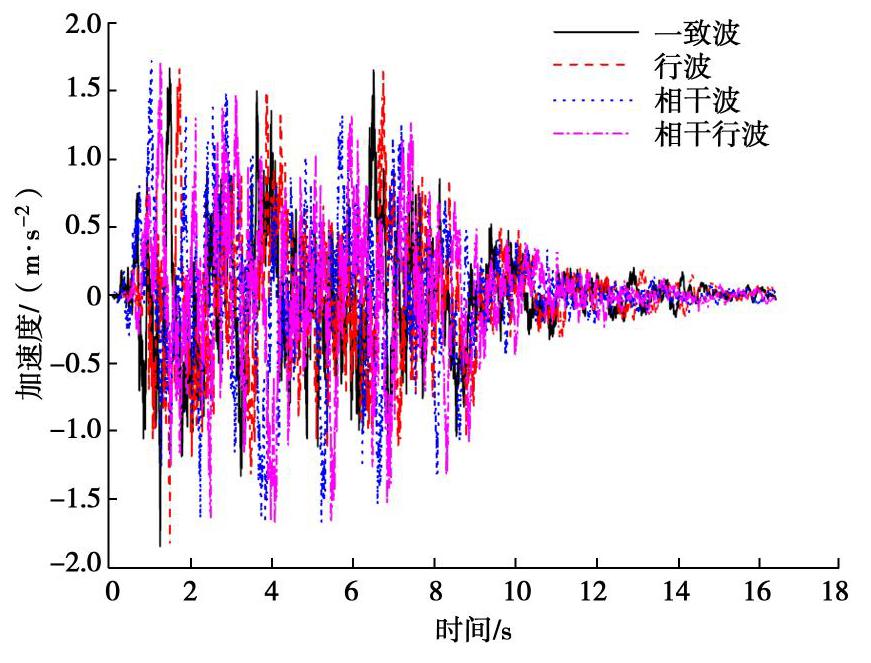
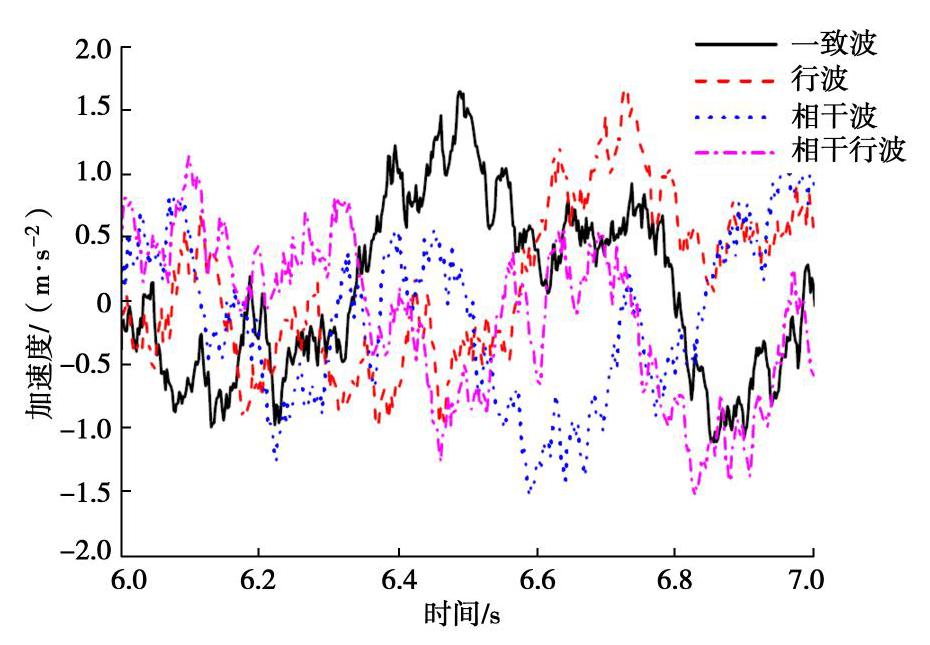
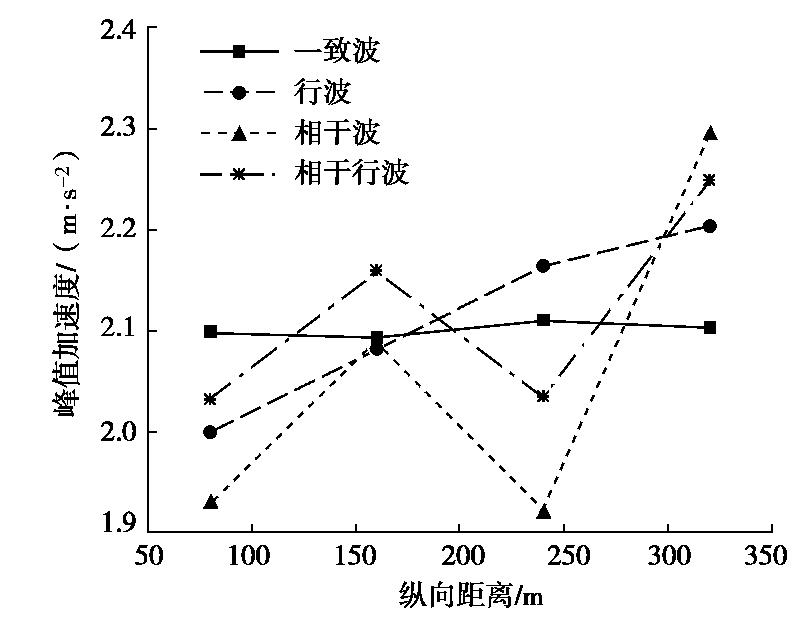
摘要: 采用数值模拟的方法对非一致激励下土–隧道体系的地震响应进行研究,旨在探究非一致激励下地下结构的响应规律及其与一致激励下响应的差异。首先基于相干函数、功率谱函数以及包络函数进行了多点相关的人工地震动合成,并通过与目标功率谱的对比验证了所合成人工波的合理性。然后对生成的地震波进行批处理,得到可用于计算的人工地震波,包括一致波、行波、相干波、相干行波。并以一精细化长大盾构隧道模型为研究对象,在其底部按单元分别进行四种波的输入,计算分析隧道结构及土体的地震响应规律。对比分析表明：在响应幅值上,当纵向距离较小时,非一致激励下地表及结构响应在整体上小于一致波,但随着纵向距离的增加,峰值加速度响应呈现递增趋势,且会超过一致激励下的响应；在频域上,非一致激励下主频处幅值相比于一致波有所减小,且主频右侧频段对应幅值增大。另外,非一致激励会引起隧道横截面内衬砌和横板产生更大的相对位移,且相干波和相干行波的影响更大,并体现出更为显著的空间变化性。因此,在进行大尺度地震模拟计算时,应适当考虑地震动空间效应的影响。
- 多点非一致激励 /
- 地下结构 /
- 地震响应 /
- 地震动空间效应 /
- 人工地震动
Abstract: The numerical simulation method is used to study the seismic response of the soil-tunnel system under non-uniform excitation. The aim is to explore the response laws of the underground structures under non-uniform excitation and its difference with those under uniform excitation. First, based on the coherence function, power spectrum function and envelope function, the multi-point correlation artificial seismic synthesis is carried out, and the rationality of the synthesized artificial waves is verified by comparing with the target power spectra. Then, the generated seismic waves are batch-processed to obtain artificial seismic waves that can be used for calculation, including four kinds of waves, such as uniform waves, traveling waves, coherent waves, and coherent traveling waves. Taking a refined long shield tunnel model as the research object, the four kinds of waves are input respectively according to the unit at the bottom of the model, and the seismic response of tunnel structure and soil is calculated and analyzed. Based on the comparative analysis, the response of the ground and the tunnel under non-uniform excitation is smaller than that under the uniform waves when the longitudinal distance is small, but the peak acceleration response increases with the longitudinal distance and exceeds the response under uniform excitation. In frequency domain, the amplitude of the dominant frequency under the non-uniform excitation is reduced compared to that of the uniform waves, and the corresponding amplitude of the right frequency band of the dominant frequency increases. In addition, the non-uniform excitation will cause greater relative displacement of the linings and transverse plates in the tunnel cross-section. The influence of coherent waves and coherent traveling waves is greater, and more significant spatial variability is exhibited. Therefore, when conducting large-scale seismic simulation calculations, due consideration should be given to the spatial effects of ground motion.
- multi-point non-uniform excitation /
- underground structure /
- seismic response /
- ground motion space effect /
- artificial ground motion

HTML全文

0. 引言

随着浅部资源逐渐枯竭,深部开采逐渐成为煤炭资源开发的常态。近十年来中国的煤炭开采深度不断增加,超过1000 m的矿井达47对^[1]。深部煤层面临高瓦斯压力、高地应力、高地温等特殊地质条件,严重威胁着深部矿山的安全开采,导致瓦斯事故发生率居高不下。据统计,2011—2016年期间煤矿发生较大以上瓦斯事故197起、死亡1667人^[2]。深部煤矿开采过程中面临的瓦斯问题是影响煤炭安全生产的主要制约因素之一。

矿山瓦斯动力灾害的本质是开采卸压作用下,煤岩体内部出现微损伤破裂并诱发大规模宏观破坏的动力灾害事故。煤岩瓦斯动力灾害的发生,伴随着煤岩能量的大量释放。声发射监测技术可为研究煤岩瓦斯灾害的诱发机制及预测方法提供科学依据。秦虎等^[3]对不同瓦斯压力作用下煤岩的声发射特征进行试验研究,分析了瓦斯压力对煤岩的软化机制,并基于声发射累计振铃计数演化特征构建了煤岩的损伤本构模型。丁鑫等^[4]基于声发射时频特征和小波变换方法,对煤岩压缩过程中的应力波的振幅频率进行分析,研究了煤岩强度和信号频带分布之间的关系。陈亮等^[5]基于不同压力条件下花岗岩的声发射试验,分析了花岗岩不同破裂阶段的声发射演化机制。熊飞等^[6]进行了相交裂隙砂岩压缩试验,分析了不同裂隙角度条件下砂岩的声发射演化特征和裂隙演化贯通直接的对应关系。李宏艳等^[7]对煤岩变形破坏过程中的累计振铃计数、声发射能量、频谱变化特征及冲击倾向特征进行了分析。

基于以上研究成果发现,学者们针对含瓦斯煤岩的力学特征研究主要集中在破坏机制和声发射演化机制,针对不同压力作用下煤岩的声发射非线性特征研究较少。基于此,本研究基于三轴渗流-应力耦合试验系统对不同瓦斯压力下煤岩的变形破坏机制及声发射特征进行了分析,对不同瓦斯压力作用下煤岩的声发射非线性演化特征进行研究,以期对煤岩瓦斯灾害的诱发机制研究提供试验和理论基础。

1. 含瓦斯煤的声发射演化特征

1.1 测试装置

煤样取自平煤八矿,埋藏深度610~710 m,该工作面平均瓦斯压力1.6 MPa,瓦斯含量16 m³/t。试验设备采用四川大学MTS815岩石力学试验系统。试验气体采用甲烷气体,分别为1, 2, 3和5 MPa,试验围压10 MPa。

1.2 瓦斯压力对煤岩声发射特征的影响

(1)声发射累计振铃计数特征

孔隙破裂、微裂隙萌生及煤颗粒错动等活动都会以弹性波的形式释放煤体内部储存的能量。声发射设备可以有效的监测煤岩内部微破裂释放的信号。声发射振铃计数是煤岩压缩变形过程中超过设定的声发射门槛值的信号数目,反映了煤岩破裂的严重程度。累计振铃计数是从声发射设备开始记录之后所有的振铃计数之和,二者都可以从不同角度反映煤岩的破裂演化特征。不同瓦斯压力作用下煤岩声发射振铃计数如图1所示。

图 1 煤岩声发射振铃计数-轴向应变演化曲线

Figure 1. Ring count-axial strain evolution curves of acoustic emission of coal

下载: 全尺寸图片幻灯片

不同瓦斯压力作用下煤岩的声发射演化特征具有相似的表现形式。在应力加载初期,煤岩的声发射信号较少,为沉寂期。随着应力水平的增加,煤岩的破裂不断增加,声发射信号进入缓慢增加期。接着煤岩进入塑性变形阶段,声发射信号进入快速增加期。最后在峰值阶段附近和峰后阶段进入活跃期和平稳期。

(2)煤岩的声发射能量特征

声发射方法可以有效地监测煤岩中裂纹的萌生、扩展及破裂特征。在全应力应变过程中,采用了声发射监测设备跟踪了煤岩在不同瓦斯压力作用下的能量演化过程。图2给出了煤岩在不同瓦斯压力作用下的AE能量随轴向应变的演化规律。含瓦斯煤岩的声发射能量特征随轴向应变的演化可以分为3个阶段,缓慢增加阶段,快速增长阶段,残余状态阶段。缓慢增加阶段对应于峰前的弹性变形阶段,这一阶段煤岩内部的损伤较少出现,煤岩中裂纹发育较少,这一阶段的声发射信号很少,整个阶段的声发射能量较低。接着进入快速增长阶段,煤岩进入峰值应力区域,这时候煤岩接近峰值应力或者已经达到峰值应力,煤岩内部出现了明显破裂,声发射累计能量几乎直线式地上升。最后煤岩进入残余状态阶段,煤岩出现残余变形,声发射累计能量继续增加,但是增加幅度有所减缓。此外,还给出了不同应力状态下煤岩声发射定位信号。声发射定位信号和累计能量相匹配,峰前阶段煤岩内部出现随机分布的声发射定位信号。当煤岩在峰值应力点附近,声发射定位信号的分布出现了一定的统计特征,集中在煤岩宏观破坏面附近。

图 2 煤岩声发射能量-轴向应变曲线

Figure 2. Acoustic emission energy-axial strain curves of coal

下载: 全尺寸图片幻灯片

2. 不同瓦斯压力作用下声发射信号的非线性特征分析

设观测到的声发射时间序列为{x(t_i)}(i=1, 2, …, n),根据“时间延迟方法”重构相空间,将时间序列拓展成m维^[8]。排列中的每一列为,{x(t_i), x(t_i+τ), x(t_i+2τ), …, x(t_i+(m-1)τ)}, τ=kΔt为延迟时间,Δt为采样周期。

嵌入维数至少是吸引子维数的2倍,即m≥2 d+1。从嵌入空间的N₀个向量中,计算其他N₀-1个向量到它的距离：

(1)

对所有的A_n(i=1, 2, …, N₀)重复这一过程,即得到关联积分函数：

(2)

式中,Heaviside函数为

(3)

关联积分可用下式求得

(4)

对于不同的r,如果这些点满足上式具有一定的线性关系,则表明声发射序列具有分形特征。图1表示了不同瓦斯压力作用下典型煤样的应力应变与声发射累计振铃数的关系。将煤岩破坏过程划分为弹性、塑性和峰后阶段,声发射序列拟合结果见图3。

图 3 不同瓦斯压力下煤岩的声发射关联维数

Figure 3. Acoustic emission correlation dimensions of coal under different gas pressures

下载: 全尺寸图片幻灯片

弹性、塑性和峰后阶段的煤岩声发射信号均表现出较好的分形特征。瓦斯压力作用下煤岩的声发射关联维数在峰前阶段先下降随后在峰后阶段出现增加。峰前阶段声发射关联维数的减小表明煤岩内部微破裂由随机分布向宏观主要破裂面聚集。峰后阶段,煤岩出现了宏观破裂,产生了大量的声发射信号。煤岩损伤出现了大幅度提升,声发射关联维数也有所增长。声发射关联维数可以作为一个有效的数学统计参量来描述这种煤岩内部微裂隙演化及破裂演化机制,可以有效的分析预测煤岩的破裂特征。可以在下一步研究中进一步细化,根据应力应变曲线划分更细致的阶段,以分析含瓦斯煤体的声发射分形特征的规律。

图4为不同瓦斯压力下煤的声发射关联维数。在各个阶段,声发射分形维数和瓦斯压力呈现正相关的关系,也就是瓦斯压力越大,声发射分形维数越高。可能是由于高瓦斯压力造成了煤岩微孔隙,微裂隙强度的降低,煤岩的破坏特征更明显,引起了声发射分形维数的提高。

图 4 不同瓦斯压力下煤岩声发射关联维数

Figure 4. Correlation dimension of acoustic emission of coal under different gas pressures

下载: 全尺寸图片幻灯片

3. 结论

利用渗流-应力耦合试验系统进行了不同瓦斯压力作用下煤岩的压缩试验,分析了煤岩不同变形破坏阶段的声发射演化特征。主要结论如下：

(1)不同瓦斯压力作用下煤岩的声发射演化特征具有相似的表现形式。在应力加载初期,煤岩的声发射信号较少,为沉寂期。随着应力水平的增加,煤岩的破裂不断增加,声发射信号进入缓慢增加期。接着煤岩进入塑性变形阶段,声发射信号进入快速增加期。最后在峰值阶段附近和峰后阶段进入活跃期和平稳期。

(2)煤岩的声发射能量和体应变演化有较好的对应关系。随着瓦斯压力的减小,声发射能量快速增加阶段曲线的变得更加陡峭,也表明煤岩的脆性破坏特性加强。随着瓦斯压力的增加,在相同的偏应力水平下,总能量耗散和耗散效率均有所增加。

(3)声发射分形数呈现在峰值段之前下降,峰后又增长的趋势。峰前阶段,分维的降低表明煤岩内部微破裂的增多和主破裂的出现,煤岩内部损伤由无序随机分布逐渐向宏观有序破坏过渡。

图 1 地震动合成流程图

Figure 1. Flow chart of synthesizing ground motion

下载: 全尺寸图片幻灯片

图 2 各点位置分布图

Figure 2. Position of points

下载: 全尺寸图片幻灯片

图 3 A₁,A₈,A₁₈,A₁₅₀模拟时程

Figure 3. Simulated time histories of points A₁, A₈, A₁₈ and A₁₅₀

下载: 全尺寸图片幻灯片

图 4 A₁,A₈,A₁₈,A₁₅₀模拟时程功率谱

Figure 4. Simulated power spectra of points A₁, A₈, A₁₈and A₁₅₀

下载: 全尺寸图片幻灯片

图 5 隧道横截面尺寸

Figure 5. Cross-sectional dimensions of tunnel

下载: 全尺寸图片幻灯片

图 6 隧道空间位置图

Figure 6. Location of tunnel

下载: 全尺寸图片幻灯片

图 7 土体计算模型

Figure 7. Soil model

下载: 全尺寸图片幻灯片

图 8 隧道计算模型

Figure 8. Tunnel model

下载: 全尺寸图片幻灯片

图 9 地震动输入示例

Figure 9. Example of ground motion input

下载: 全尺寸图片幻灯片

图 10 A₁₂₀点处4种波时程

Figure 10. Time histories of four seismic waves at point A₁₂₀

下载: 全尺寸图片幻灯片

图 11 A₁₂₀点处4种波时程放大图

Figure 11. Partial enlargement of time histories of four waves at point A₁₂₀

下载: 全尺寸图片幻灯片

图 12 土体测点布置

Figure 12. Arrangement of measuring points for soil

下载: 全尺寸图片幻灯片

图 13 隧道测点布置

Figure 13. Arrangement of measuring points for tunnel

下载: 全尺寸图片幻灯片

图 14 不同激励方式下地表80 m处加速度响应

Figure 14. Acceleration responses under different waves at 80 m below surface of soil

下载: 全尺寸图片幻灯片

图 15 不同激励方式下地表峰值加速度响应随纵向距离的变化曲线

Figure 15. Peak ground acceleration responses at different longitudinal distances under different waves

下载: 全尺寸图片幻灯片

图 16 不同激励方式下160 m处隧道衬砌顶部加速度响应

Figure 16. Acceleration responses of lining top at 160 m under different waves

下载: 全尺寸图片幻灯片

图 17 不同激励方式下320 m处隧道衬砌顶部加速度响应

Figure 17. Acceleration responses of lining top at 320 m under different waves

下载: 全尺寸图片幻灯片

图 18 不同激励方式下衬砌顶部峰值加速度响应变化曲线

Figure 18. Peak acceleration responses of lining top at different longitudinal distances under different waves

下载: 全尺寸图片幻灯片

表 1 相干函数模型参数^[19]

Table 1 Parameters of coherent function model

$v_{c}$ $v_{c}$ /(m·s^-1)	A	$α$ $α$	$k$ $k$ /m	$ω_{0}$ $ω_{0}$ /(rad·s^-1)	b
1000	0.626	0.022	19700	12.69	3.47

下载: 导出CSV

表 2 功率谱模型参数

Table 2 Parameters of power spectrum model

S₀	$ω_{g}$ $ω_{g}$ /(rad·s^-1)	$ω_{f}$ $ω_{f}$ /(rad·s^-1)	$ζ_{g}$ $ζ_{g}$ /(rad·s^-1)	$ζ_{f}$ $ζ_{f}$ /(rad·s^-1)
2.25×10^-3	7.539	0.754	0.85	0.85

下载: 导出CSV

表 3 包络函数模型参数^[21]

Table 3 Parameters of envelope function model

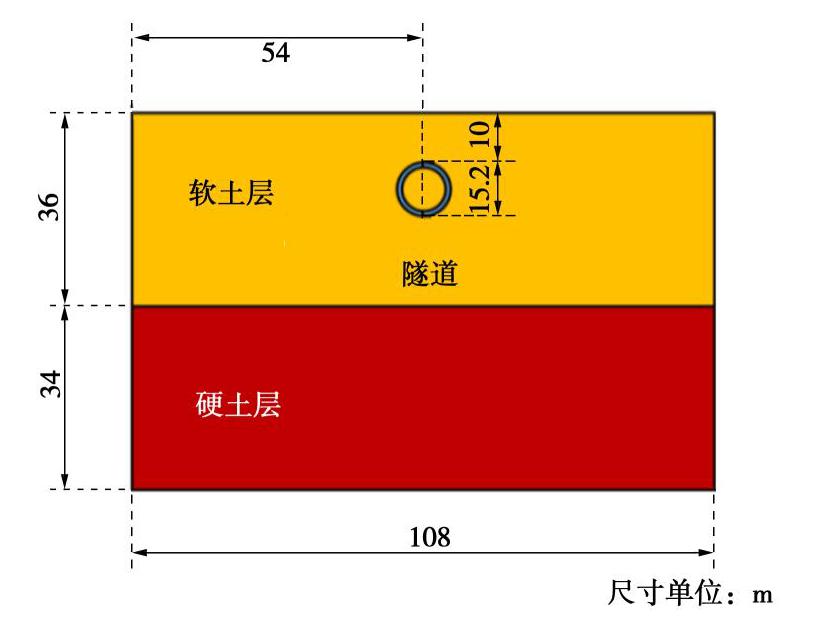
$t_{1}$ $t_{1}$ /s	$t_{2}$ $t_{2}$ /s	c
0.8	7	0.35

下载: 导出CSV

表 4 土体参数

Table 4 Parameters of soils

土层	深度/m	密度 $ρ$ $ρ$ /(kg/m³)	Davidenkov模型参数
土层	深度/m	密度 $ρ$ $ρ$ /(kg/m³)	$G_{\max}$ $G_{\max}$ /(10⁸ Pa)	$ν$ $ν$	A	B	$γ_{0}$ $γ_{0}$	$ζ$ $ζ$	v/(m·s^-1)
软土	36	1920	1.728	0.41	1	0.38	9.67×10^-4	3×10^-3	300
硬土	34	1980	4.009	0.35	1	0.35	1.77×10^-3	3×10^-3	450

下载: 导出CSV

表 5 地表峰值加速度变化率

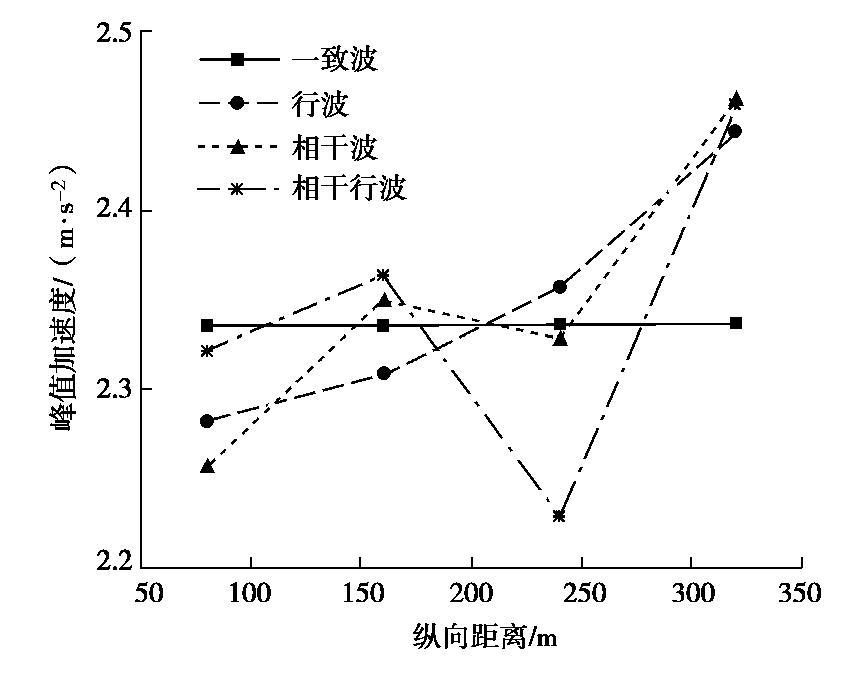
Table 5 Change rates of peak ground acceleration (%)

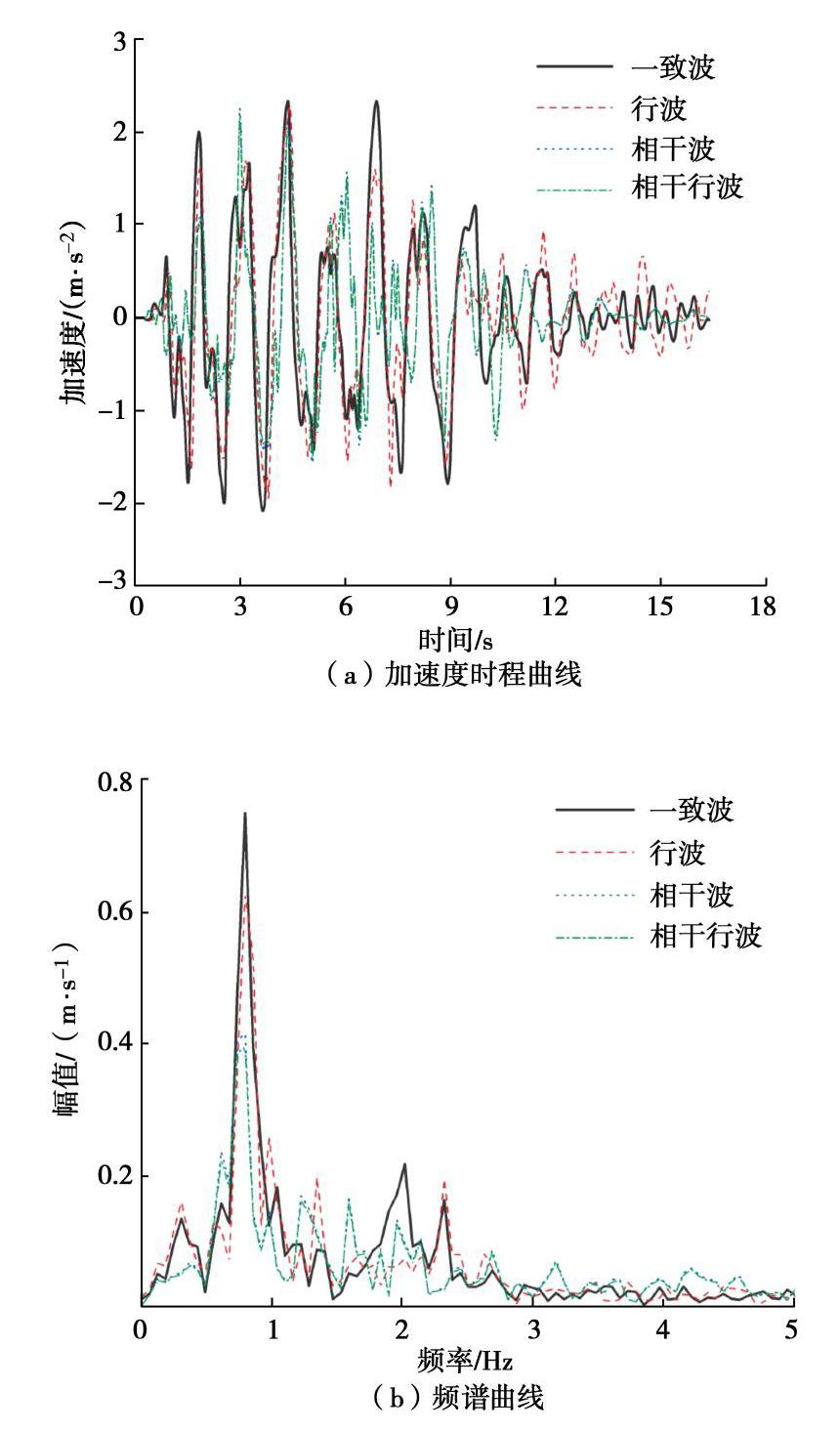
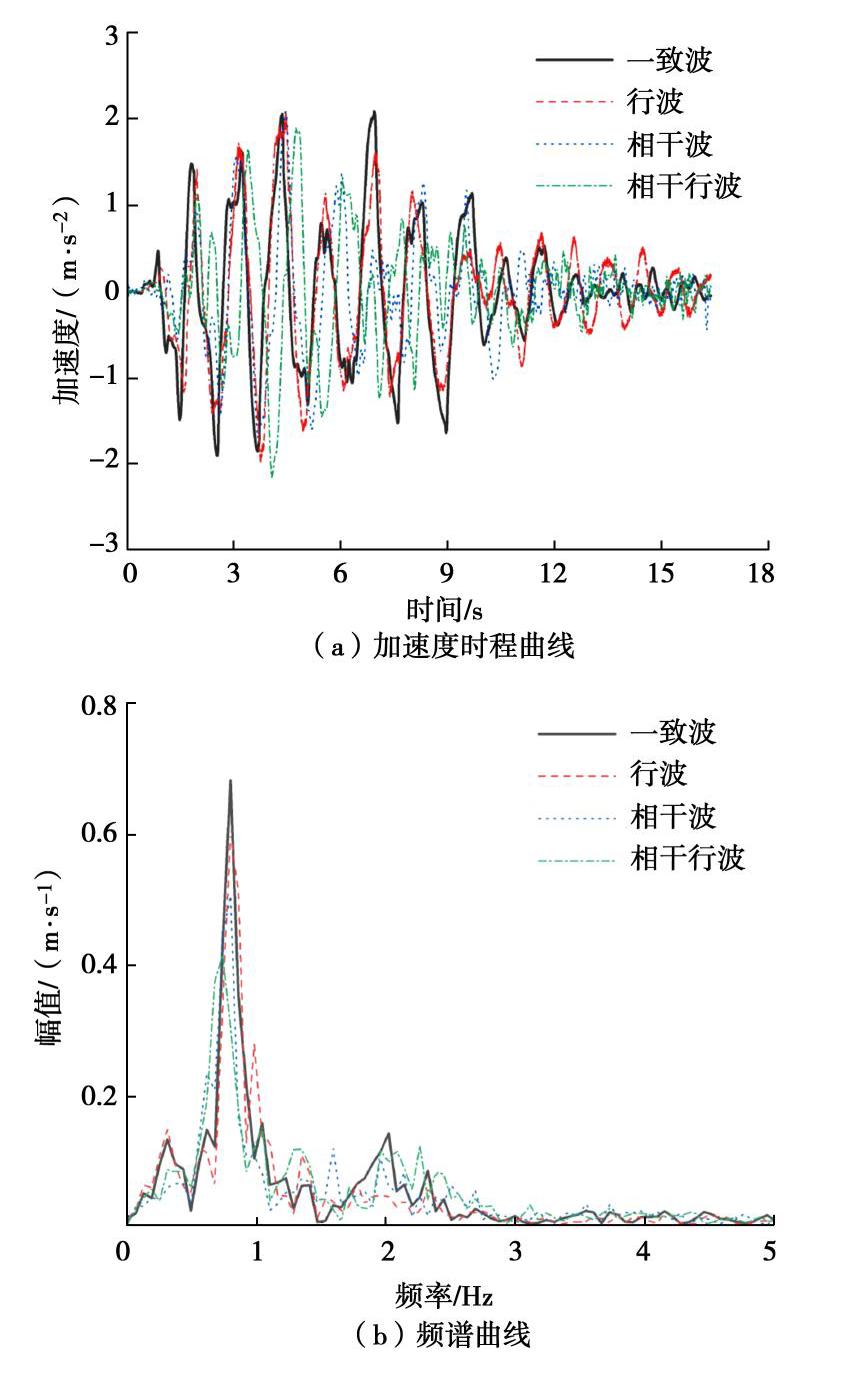
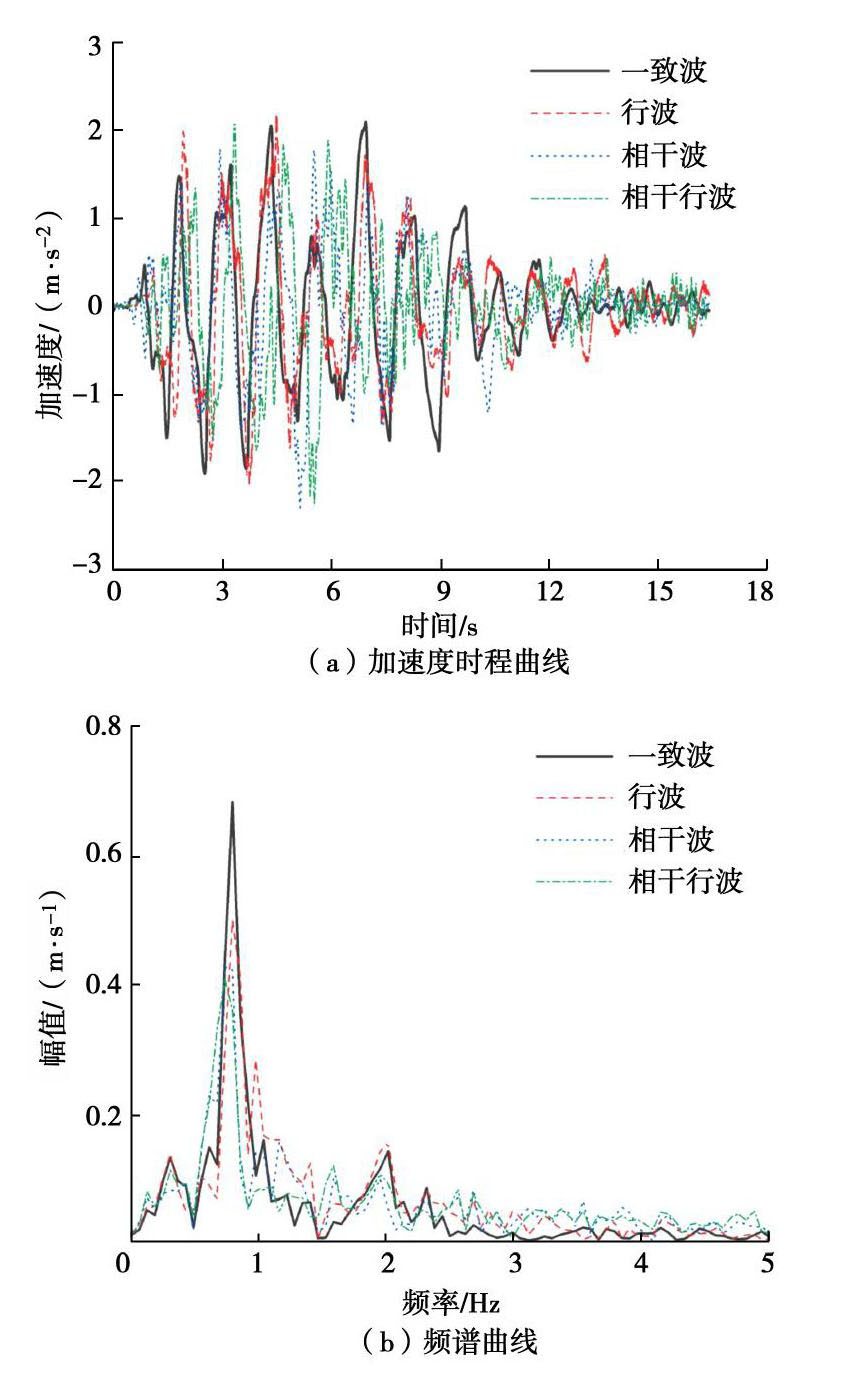
输入方式	纵向长度/m
输入方式	80	160	240	320
行波	-2.29	-1.14	0.89	4.62
相干波	-3.39	0.62	-0.36	5.42
相干行波	-0.59	1.20	-4.63	5.23

下载: 导出CSV

表 6 衬砌顶部峰值加速度变化率

Table 6 Change rates of peak acceleration of lining top (%)

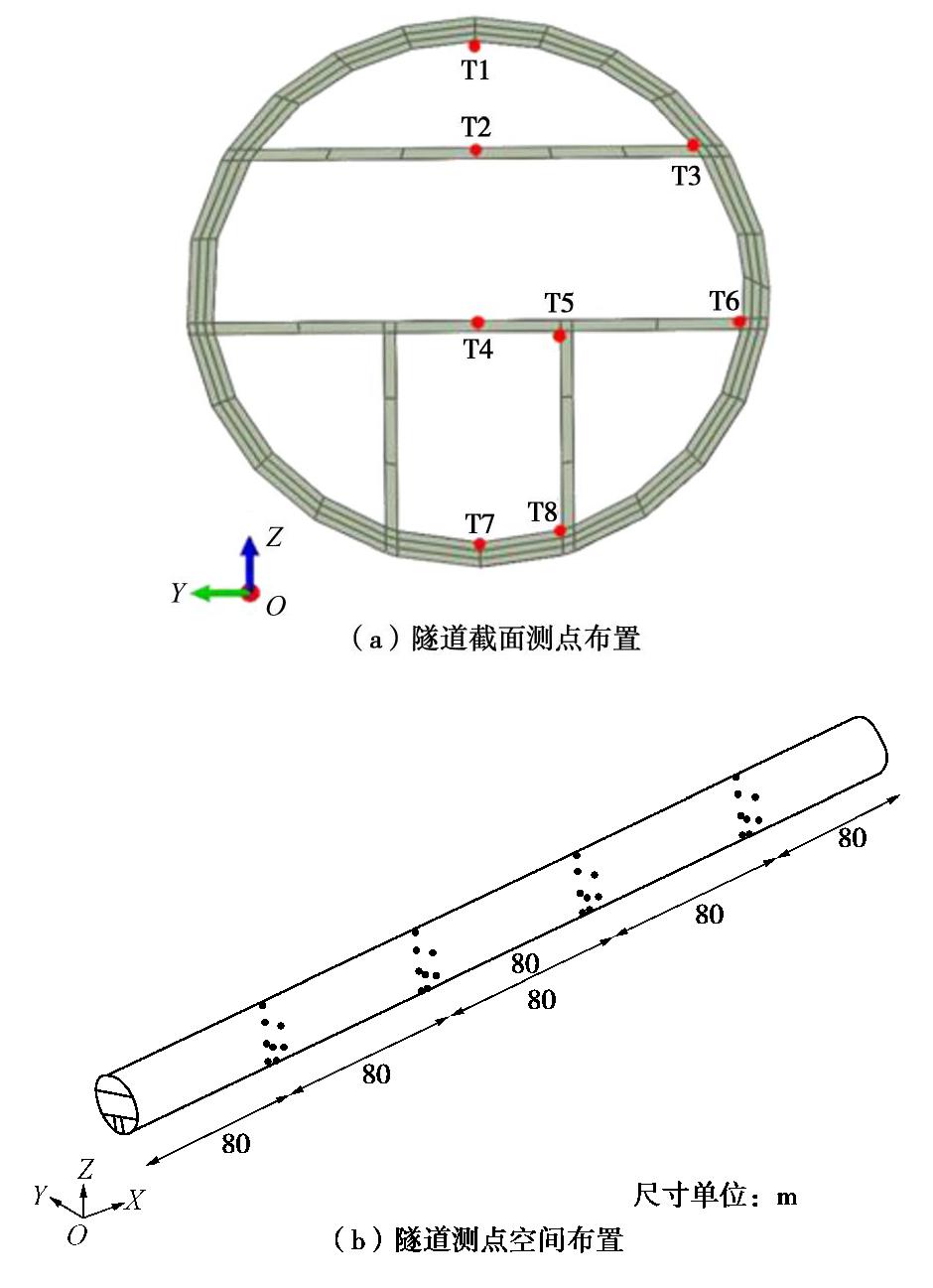
输入方式	纵向长度/m
输入方式	80	160	240	320
行波	-4.76	-0.57	2.51	4.79
相干波	-8.03	-0.25	-8.95	9.18
相干行波	-3.17	3.12	-3.63	6.96

下载: 导出CSV

表 7 不同地震波作用下隧道衬砌顶底（T1与T7）的最大相对位移

Table 7 Maximum relative displacements between tunnel lining top and bottom (T1 and T7) under different seismic waves

截面	一致波		行波		相干波		相干行波
截面	相对位移/m	变化率/%	相对位移/m	变化率/%	相对位移/m	变化率/%	相对位移/m	变化率/%
x=80 m	-0.0006	—	-0.0019	217	-0.0120	1900	-0.0142	2267
x=160 m	-0.0006	—	-0.0009	50	-0.0045	650	0.0102	1800
x=240 m	-0.0006	—	-0.0006	0	-0.0030	400	0.0053	983
x=320 m	-0.0006	—	0.0008	233	0.0124	2167	0.0106	867

下载: 导出CSV

表 8 不同地震波作用下隧道上下横板中间（T2与T4）的最大相对位移

Table 8 Maximum relative displacements between upper and lower tunnel horizontal plates (T2 and T4) under different waves

截面	一致波		行波		相干波		相干行波
截面	相对位移/m	变化率/%	相对位移/m	变化率/%	相对位移/m	变化率/%	相对位移/m	变化率/%
x=80 m	-0.0004	—	-0.0007	75	-0.0171	4175	-0.0042	950
x=160 m	-0.0003	—	-0.0004	33	-0.0062	1967	0.0072	2500
x=240 m	-0.0003	—	-0.0003	0	-0.0051	1600	-0.0093	3000
x=320 m	-0.0003	—	0.0005	267	0.0172	5833	0.0089	3067

下载: 导出CSV

参考文献(22)

[1]	IIDA H, HIROTO T, YOSHIDA N, et al. Damage to Daikai subway station[J]. Soils & Foundations, 1996, 36: 283-300.
[2]	DOWDING C H, ROZAN A. Damage to rock tunnels from earthquake shaking[J]. Journal of the Soil Mechanics and Foundation Division, 1978, 104(2): 175-191.
[3]	JAYALAKSHMI S, RAGHUKANTH S T G. Regional ground motion simulation around Delhi due to future large earthquake[J]. Natural Hazards, 2016, 82(3): 1-35.
[4]	YENIER E, ATKINSON G M. An equivalent point‐source model for stochastic simulation of earthquake ground motions in California[J]. Bulletin of the Seismological Society of America, 2015, 105(3): 1435-1455. doi: 10.1785/0120140254
[5]	屈铁军, 王前信. 空间相关的多点地震动合成(I)基本公式[J]. 地震工程与工程振动, 1998, 18(1): 8-15. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC801.001.htm QU Tie-jun, WANG Qian-xin. Simulation of spatial correlative time histories of multi-point ground motion, part I: fundamental formulas[J]. Earthquake Engineering and Engineering Vibration, 1998, 18(1): 8-15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC801.001.htm
[6]	屈铁军, 王前信. 空间相关的多点地震动合成(Ⅱ)合成实例[J]. 地震工程与工程振动, 1998, 18(2): 25-32. QU Tie-jun, WANG Qian-xin. Simulation of spatial correlative time histories of multi-point ground motion, part Ⅱ: application of fundamental formulas[J]. Earthquake Engineering and Engineering Vibration, 1998, 18(2): 25-32. (in Chinese)
[7]	杨庆山, 姜海鹏. 基于相位差谱的时-频非平稳人造地震动的反应谱拟合[J]. 地震工程与工程振动, 2002, 22(1): 32-38. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200201006.htm YANG Qing-shan, JIANG Hai-peng. Generation of response-spectrum-compatible ground motions based on phase-difference spectrum[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(1): 32-38. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200201006.htm
[8]	WANG D, LI J. Physical random function model of ground motions for engineering purposes[J]. Science China (Technological Sciences), 2011, 54(1): 175-182. doi: 10.1007/s11431-010-4201-3
[9]	夏友柏, 王年桥, 张尚根. 一种合成多点地震动时程的方法[J]. 世界地震工程, 2002, 18(1): 119-122. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC200201022.htm XIA You-bai, WANG Nian-qiao, ZHANG Shang-gen. A simulation method for spatial correlative time histories of multi-point ground motion[J]. World Earthquake Engineering, 2002, 18(1): 119-122. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC200201022.htm
[10]	吴祚菊. 空间相关性地震动生成及地下管线非一致性激励研究[D]. 成都: 西南交通大学, 2015. WU Zuo-ju. Generation of Spatial Correlation Ground Motion and the Study of Inconsistency Motivation About Underground Pipeline[D]. Chengdu: Southwest Jiaotong University, 2015. (in Chinese)
[11]	GAO Yu-feng, WU Yong-xin, LI Bing. Simplified method for simulation of ergodic spatially correlated seismic ground motion[J]. Applied Mathematics and Mechanics (English Edition), 2011, 32(10): 1297-1314. doi: 10.1007/s10483-011-1501-x
[12]	姚二雷, 苗雨, 陈超. 基于奇异值分解的空间变异地震动模拟[J]. 华中科技大学学报(自然科学版), 2016, 44(10): 22-25. https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201610005.htm YAO Er-lei, MIAO Yu, CHEN Chao. Simulation of spatially varying ground motions based on singular value decomposition[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(10): 22-25. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201610005.htm
[13]	范立础, 王君杰, 陈玮. 非一致地震激励下大跨度斜拉桥的响应特性[J]. 计算力学学报, 2001, 18(3): 358-363. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG200103021.htm FAN Li-chu, WANG Jun-jie, CHEN Wei. Response characteristics of long-span cable-stayed bridges under non-uniform seismic action[J]. Chinese Journal of Computational Mechanics, 2001, 18(3): 358-363. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG200103021.htm
[14]	XIA H, HAN Y, ZHANG N, et al. Dynamic analysis of train-bridge system subjected to non-uniform seismic excitations[J]. Earthquake Engineering & Structural Dynamics, 2006, 35(12): 1563-1579.
[15]	SURH H B, RYU T Y, PARK J S, et al. Seismic response analysis of a piping system subjected to multiple support excitations in a base isolated NPP building[J]. Nuclear Engineering and Design, 2015, 292: 283-295.
[16]	杨庆山, 刘文华, 田玉基. 国家体育场在多点激励作用下的地震反应分析[J]. 土木工程学报, 2008, 41(2): 35-41. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200802007.htm YANG Qing-shan, LIU Wen-hua, TIAN Yu-ji. Response analysis of national stadium under specially variable earthquake ground motions[J]. China Civil Engineering Journal, 2008, 41(2): 35-41. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200802007.htm
[17]	陈健云, 林皋. 多点输入随机地震动拱坝—地基体系反应分析[J]. 世界地震工程, 2000, 16(3): 39-43. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC200003008.htm CHEN Jian-yun, LIN Gao. Random response analysis of arch dam-foundation system subjected to multi-input seismic excitation[J]. World Earthquake Engineering, 2000, 16(3): 39-43. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC200003008.htm
[18]	田利, 李宏男. 多维多点地震动激励下折线型输电塔线体系反应分析[J]. 土木工程学报, 2012, 45(增刊1): 131-135. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2012S1026.htm TIAN Li, LI Hong-nan. Seismic response of fold linear type transmission tower-line system under multi-component multi-support excitations[J]. China Civil Engineering Journal, 2012, 45(S1): 131-135. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2012S1026.htm
[19]	HARICHANDRAN R S, HAWWARI A, SWEIDAN B N. Response of long-span bridges to spatially varying ground motion[J]. Journal of Structural Engineering, 1996, 122(5): 476-484.
[20]	CLOUGH R W, PENZIEN J. Dynamics of Structures[M]. New York: McGraw Hill, 1993.
[21]	JENNINGS P C, HOUSNER G W, TSAI N C. Simulated Earthquake Motions[R]. Pasadena: California Institute of Technology, 1968.
[22]	庄海洋, 陈国兴, 梁艳仙, 等. 土体动非线性黏弹性模型及其ABAQUS软件的实现[J]. 岩土力学, 2007, 28(3): 436-442. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200703003.htm ZHUANG Hai-yang, CHEN Guo-xing, LIANG Yan-xian, et al. A developed dynamic viscoelastic constitutive relations of soil and implemented by ABAQUS software[J]. Rock and Soil Mechanics, 2007, 28(3): 436-442. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200703003.htm

施引文献(16)

期刊类型引用(9)

1.	王成功，杨国涛. 列车移动荷载与非一致地震动作用下轨道-路基系统动力响应. 振动与冲击. 2024(18): 297-305 . 百度学术
2.	任璐瑶，吴镇杰，黄啟超，关振长. 考虑轴力影响的盾构隧道纵向地震响应解析. 岩土力学. 2024(10): 2971-2980 . 百度学术
3.	彭浩，高智能，胡世丽，谷音. 非一致地震波动输入下大型钢筋混凝土框架结构-地基体系地震响应规律. 地震工程学报. 2023(04): 887-893 . 百度学术
4.	付晓东，丁海锋，袁维，王宏超，周永强，盛谦. 非一致性地震作用下穿越破碎带长大隧道衬砌结构动力变形分析. 中国铁道科学. 2023(05): 116-126 . 百度学术
5.	江辉，宋光松，郭辉，曾聪，卢文良，刘展铄，周勇政，何友娣. 跨“V”形峡谷大跨度铁路悬索桥减震研究. 中国铁道科学. 2022(01): 63-74 . 百度学术
6.	朱俊，李小军，梁建文. 地震波斜入射地下隧道地震响应：2.5维FE-BE耦合模拟. 岩土工程学报. 2022(10): 1846-1854 . 本站查看
7.	沈万虎，丁祖德，资昊. 强震下成层土盾构隧道地震响应及结构安全性分析. 科技通报. 2022(11): 9-13+19 . 百度学术
8.	许成顺，胡正一，史跃波，钟紫蓝，赵密. SV波斜入射下预制拼装式综合管廊接口的地震响应规律. 北京工业大学学报. 2022(12): 1215-1225 . 百度学术
9.	周永强，盛谦，李娜娜，付晓东. 非一致性地震动作用下某长大隧洞动力响应的时空效应初步研究. 岩土力学. 2021(08): 2287-2297 . 百度学术

其他类型引用(7)

资源附件(0)

图(18) / 表(8)

计量

文章访问数: 315
HTML全文浏览量: 28
PDF下载量: 185
被引次数: 16

0. 引言
1. 含瓦斯煤的声发射演化特征
1.1 测试装置
1.2 瓦斯压力对煤岩声发射特征的影响
2. 不同瓦斯压力作用下声发射信号的非线性特征分析
3. 结论

非一致激励下长大盾构隧道结构地震响应分析 English Version

作者简介: 王国波(1979—),男,博士,教授,主要从事工程结构的抗震分析研究工作。E-mail：wgb16790604@126.com

通讯作者: 孙富学, E-mail：sunfuxue@163.com

计量

出版历程