DEM analysis of evolution law of bond degradation for structured soils
-
摘要: 结构性土体通常指粒间含有胶结的土体,可看成一种特殊的胶结颗粒材料,探明结构性土体的胶结破损演化规律是加深结构性土体宏微观力学性质认识及建立结构性土本构模型的关键。由于试验手段难以定量获取胶结破损信息,通过离散单元法分析了结构性土体的胶结破损演化规律。首先采用相对完备的胶结接触模型建立了结构性土体离散元试样,接触模型考虑了颗粒及胶结物质的抗转动和抗扭转作用以及胶结尺寸对刚度和强度的影响;然后开展了结构性土侧限压缩、等向压缩、等应力比压缩以及常规三轴和真三轴试验的离散元数值分析,再现了结构性土的主要宏观力学特征;在此基础上的胶结破损演化分析表明胶结破损参量B0演化具有明显的应力路径相关性,而新提出的破损参量Bσ应力路径相关性低,通过Bσ与等效塑性应变的指数函数关系,可以描述结构性土体的胶结破损演化情况。
-
关键词:
- 结构性土 /
- 胶结颗粒材料(理想结构性土) /
- 离散单元法 /
- 胶结破损演化 /
- 本构模型
Abstract: The evolution of bond degradation is essential for analyzing the macro-and micro-scopic behaviors and establishing constitutive models for structured soils with cementation bond which is a kind of bonded granular material. The discrete element method is employed to analyze the evolution of bond degradation on account of the disadvantage of laboratory tests in bond breakage quantitative analysis. First, the discrete numerical sample is generated by installing a relatively completed bond contact model incorporating the interparticle rolling and twisting resistances and the influences of bond size on the contact stiffness and strength. The DEM simulation reproduces the key mechanical behaviors of one-dimensional compression, isotropic and anisotropic compressions, conventional triaxial and true triaxial tests on the DEM sample. The results show that the evolution of the degradation variable B0 is stress-path-dependent, while a new degradation variable Bσ is roughly stress-path-independent. An exponential function is recommended for Bσto describe the degradation of soil structure. -
0. 引言
面板堆石坝安全稳定的核心问题之一是坝体变形控制,而变形控制的基础是对原级配堆石料力学变形特性的准确把握。堆石料级配较宽,国内一些堆石坝工程中使用的堆石筑坝料最大粒径可达800~1600 mm[1],目前通常采用缩尺后的堆石料开展室内试验,以此获取堆石料的力学变形参数。然而,缩尺后的堆石料级配较原级配发生了改变,级配的变化改变了颗粒粒径的构成,使堆石料填充特性也发生改变;同时,颗粒强度、颗粒粗糙度等与粒径相关的量也因缩尺发生变化,从而造成缩尺后堆石料的力学变形特性与原级配堆石料的存在差异,即堆石料的缩尺效应。
自20世纪40年代Alan等[2]首次提出堆石料缩尺效应以来,伴随着众多堆石坝工程的建设,世界各国学者针对堆石料缩尺效应开展了大量研究。纵观现有堆石料缩尺效应研究,大多集中在力学特性[3-10]和变形特性[5,8,10-14]方面,填充特性方面涉及甚少,已有的填充特性方面研究也仅涉及堆石料压缩性[15-16]和制样干密度[8,17-19]的缩尺效应研究。现有堆石料缩尺效应研究发现了一些规律,取得了诸多有价值的成果。但由于影响堆石料缩尺效应的因素众多[6,8,12,17,20],如缩尺方法、颗粒破碎、颗粒级配、颗粒形状、制样标准等,在各种因素的交互影响下,堆石料缩尺效应仍是一个复杂的课题。目前对缩尺引起的强度和变形差异的机理还不清楚,今后应将宏细观层面的缩尺效应研究相互结合才能有更大的突破[21]。
堆石料的填充特性可由试样孔隙率、有效孔隙率、承力/填充颗粒占比、颗粒堆积结构特征等宏细观参量描述,其与堆石料的力学变形特性有着密切的关系。缩尺会改变堆石料填充特性,不同缩尺比堆石料试样的颗粒破碎程度不同[4,22],颗粒的破碎将改变堆石料级配,进一步促使堆石料填充特性及其演化发生改变。颗粒破碎是影响堆石料缩尺效应的主要因素[6,23-24],缩尺引起的填充特性差异和颗粒破碎引起的填充特性改变共同导致了堆石料试样力学响应的差异性和缩尺效应的复杂性。鉴于此,以堆石料填充特性为切入点,围绕堆石料填充特性的宏细观演化,开展堆石料缩尺效应研究将对进一步认识堆石料复杂力学响应及其缩尺效应产生机理有重要意义。
然而,受当前试验技术水平的限制,室内试验手段难以实时监测一些描述堆石料填充特性的演化,特别是堆石料填充特性细观层面的演化,在揭示堆石料缩尺效应的产生机理方面存在不足。离散元方法能反映非连续介质的离散性及其复杂、多样的结构特征,适合散粒体材料力学响应的模拟,并能开展传统试验手段难以企及的细观层面研究,是探究颗粒材料力学变形特性细观机理的有力工具,为从细观层面开展堆石料填充特性的缩尺效应研究提供了可能。
综上,本文基于离散元方法,以堆石料的填充特性为切入点,考虑颗粒破碎的影响,通过分析试样孔隙率、有效孔隙率、悬浮颗粒体积分数、有效配位数、配位数频率分布等描述堆石料填充特性的宏细观参量的演化,从宏、细观层面探讨堆石料填充特性的缩尺规律,以期更全面认识堆石料的缩尺效应,并进一步揭示堆石料缩尺效应产生的机理。
1. 颗粒破碎模拟方法
基于离散元法模拟颗粒破碎主要有黏结颗粒法(bonded-particle method,BPM)和碎片替代法(fragment replacement method,FRM)2种方法[25]。黏结颗粒法的颗粒破碎程度有限且只适用小规模的模拟计算,基于FRM的颗粒破碎模拟方法能结合室内试验进行较大规模的数值模拟研究。为此,本研究中采取FRM模拟颗粒破碎,而基于FRM模拟颗粒破碎需要考虑颗粒破碎准则和碎片替换模式两个主要问题。
1.1 颗粒破碎准则
McDowell等[26]在研究中采用八面体剪应力破坏准则,开展了颗粒集合体侧限固结压缩数值模拟研究,模拟试验结果与室内试验结果相符,表明该破碎准则模拟颗粒破碎的合理性。本研究中同样采用该破碎准则,八面体剪应力可表示为
q=13[(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]1/2, (1) 式中,
σ1 ,σ2 ,σ3 分别为第一、二、三主应力。离散元方法中,一个颗粒的应力张量σij 可定义为σij=1V∑ncfcjdci, (2) 式中,V为颗粒的体积,
nc 为该颗粒接触的总数,fcj 为接触力,dci 为接触中心的支向量,σ1 ,σ2 和σ3 则分别对应于σ11 ,σ22 和σ33 。当离散元模拟过程中计算得到的颗粒的八面体剪应力大于设定的容许八面体剪应力[q] 时,则判定颗粒发生破碎。De Bono等[27]指出容许八面体剪应力[q] =0.9σf =0.9Ff/d2 。式中,σf 为颗粒的破碎强度,Ff 为单颗粒径向压缩试验中颗粒的峰值破碎力,d为颗粒的粒径。天然脆性颗粒材料,如砂砾、碎石、堆石料等,存在一定缺陷,如微裂缝、微孔洞等,使得天然脆性颗粒材料的破碎强度呈现出Weibull分布特性[28]。此外,脆性材料的破碎强度还呈现出明显的尺寸效应[29-30]。研究中考虑脆性颗粒材料破碎强度的尺寸效应和Weibull分布特性。根据Weibull分布理论[28,30],每个颗粒的破碎强度
σf 可表示为σf=[ln(1/Ps(d))]1/m(d/d0)−(3/m)σ0, (3) 式中,
Ps(d) ,m ,σ0 和d0 分别为颗粒存活概率、颗粒破碎强度的Weibull模量、颗粒特征破碎强度和颗粒特征破碎强度对应的颗粒粒径。其中颗粒破碎强度的尺寸效应通过(d/d0)−3/m 体现。1.2 碎片替代模式
现有研究中采用了多种多样的二维/三维碎片替换模式[25]。碎片替换模式对颗粒集合体破碎的演变有明显的影响,不同的碎片替换模式会导致模拟试验后的颗粒级配有很大差异[31-32],而颗粒级配特性又是影响颗粒集合体力学变形特性的主要因素之一[33]。
Ciantia等[32]根据Apollonian排列方式构建了5种碎片替换模式,并开展颗粒集合体的侧限压缩数值试验,研究表明,包含3种尺寸共14个“碎片“的Apollonian堆积态碎片替换模式(图1)能在保证计算效率的同时,准确反映颗粒材料真实的力学行为响应。为此,本研究选取该碎片替换模式开展相关研究。
数值试验中,颗粒的破碎过程:每计算n步后,开始遍历所有颗粒,当第i个颗粒受力情况满足预设的破碎准则时,启动基于FISH语言编译的碎片替换子程序,在将要发生破碎的原颗粒所占空间中生成图1所示的碎片替换模式,然后删除原颗粒,完成替换;替换后在相对整个模拟过程非常短的时步内以较低的速度逐渐膨胀碎片子颗粒,并通过颗粒速度判定子程序来尽可能地减少颗粒膨胀造成的局部颗粒重叠,避免不合实际的局部应力增大现象。
2. 数值试验准备
2.1 试验级配曲线
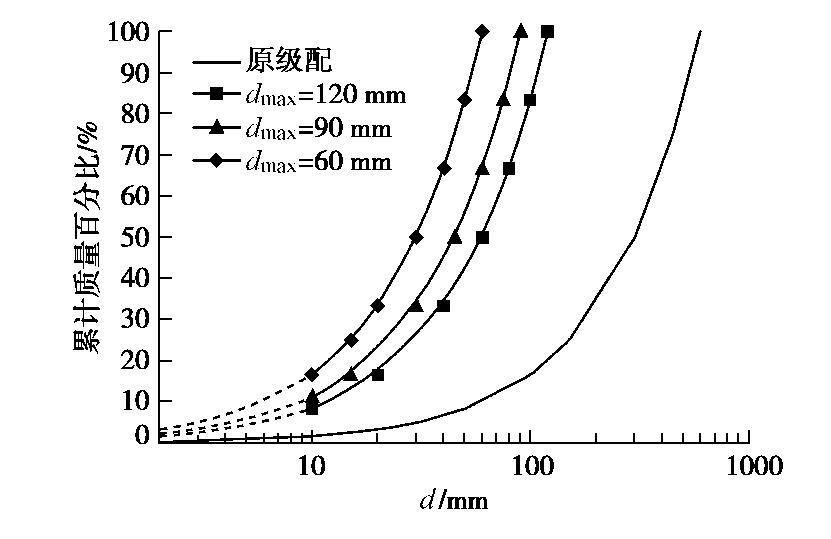
本研究采用离散元软件PFC3D[34]开展常规三轴数值剪切试验,研究中为避免颗粒形状的影响,使用基本单元“圆球“代替堆石料。通过相似级配法对最大颗粒粒径为600 mm的原级配进行缩尺,得到最大粒径
dmax 分别为60,90,120 mm的3条平行试验级配曲线,如图2所示。图中级配曲线根据Tyler公式[35](pi=100(di/dmax)3−D )得到。式中,pi 为粒径小于di 颗粒的累计质量百分比,D为级配曲线的分形维数。考虑到个人计算机的模拟计算效率,数值试验中试样的颗粒数目不宜过多,且试样级配宽度不能过大。为了控制初始试样中颗粒的数目,本研究中D取2.0,dmin 取10 mm,粒径小于10 mm的颗粒按相同质量全部等效为10 mm颗粒。2.2 数值试样
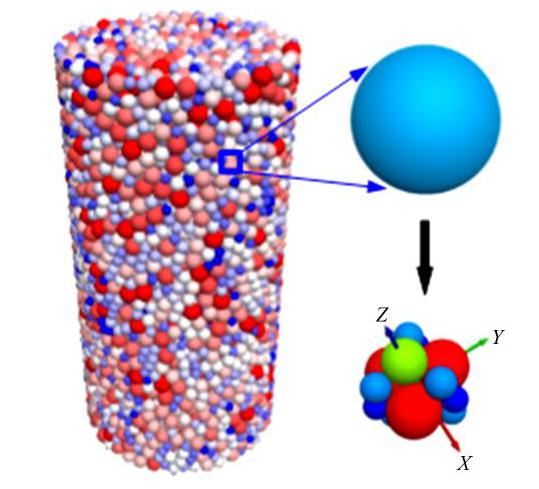
制样采用的径径比为5,在由圆柱形侧边墙和上下加载板封闭而成的圆柱形空间内按缩尺后的三种级配通过粒径膨胀法分别生成尺寸(D×H)为300 mm×600 mm、450 mm×900 mm和600 mm×1200 mm的试样,对应级配的最大颗粒粒径
dmax 分别为60,90,120 mm。对于级配不同的试样,为达到相同的初始密度状态,研究中采用Zhou等[36]的制样方法,该方法与同一相对密度或同一压实功制样类似。设定100 kPa围压时的试样为初始试样,对应孔隙率为初始孔隙率。为得到较为密实的初始试样,制样过程中取颗粒摩擦系数为0.1。最终制得最大粒径为60,90,120 mm试样的初始孔隙率分别为30.65%,28.23%和27.03%。可知,同一原级配曲线相似级配缩尺后,最大粒径越大,试样密度越大,这与文献[17,19,37]结论一致。3种不同尺寸的初始试样如图3所示。
颗粒间的相互作用采用Hertz-Mindlin接触模型来描述,生成初始试样之后,试验过程中颗粒摩擦系数取0.5,颗粒参数和颗粒破碎准则参数依据文献[31,38]取值,离散元模拟参数如表1所示。
表 1 离散元模拟参数Table 1. Input parameters for DEM simulation类别 参数 取值 颗粒参数 密度/(kg·m-3) 2650 摩擦系数 μ 0.5 剪切模量G/GPa 28 泊松比 ν 0.15 颗粒破碎准则参数 特征粒径 d0 /mm28 特征破碎强度 σ0 /MPa18.2,14.0 韦伯模量m 2.65 本研究中,颗粒破碎只发生在初始试样施加围压到试验围压以及之后剪切试验过程中。此外,为对比不破碎与破碎的差异性,另进行了一组不考虑颗粒破碎的模拟试验,即共有不考虑颗粒破碎的缩尺试样组、考虑颗粒破碎且
σ0=18.2 MPa 的缩尺试样组和考虑颗粒破碎且σ0=14.0 MPa 的缩尺试样组。各组模拟试验均考虑3种试验围压,即0.4,0.8,1.2 MPa。为方便描述,给各组试样编号,编号规则如D60CP400,其中D为“diameter“的首字母,60表示试样中最大颗粒粒径为60 mm,CP是“confining pressure(围压)”的简写,400表示试验围压为0.4 MPa(400 kPa),其他试样编号以此类推。
3. 数值试验结果
3.1 缩尺试样力学响应和颗粒破碎率
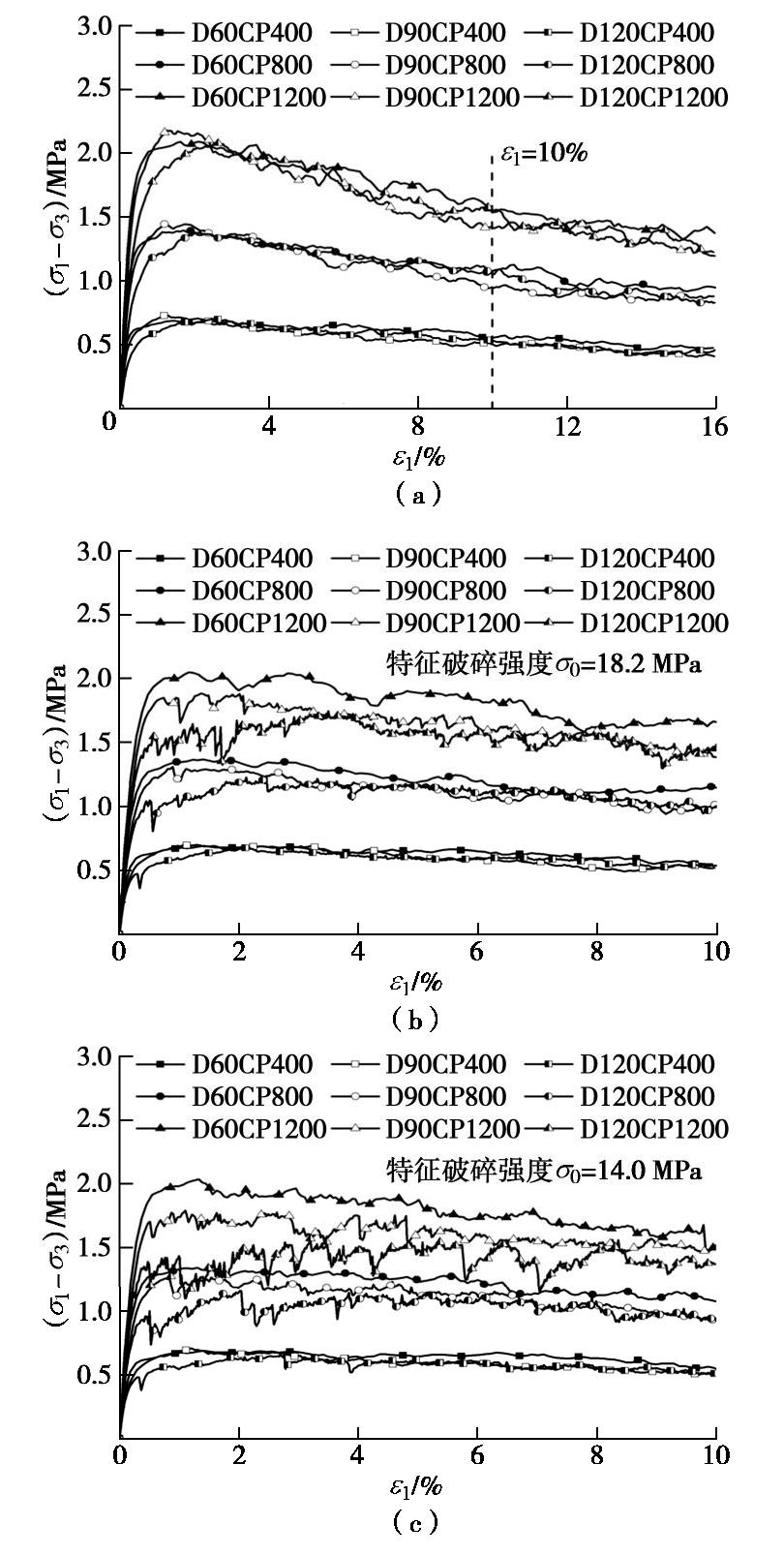
各缩尺试样组的应力–应变曲线如图4所示。图4(a)为不考虑颗粒破碎的试样,图4(b),(c)为考虑颗粒破碎的试样。初始试样压实度较高,轴向应变较小(约1%)时达到强度峰值,而对应的初始孔隙率较大(27%~31%)。这主要是由于球形颗粒间易形成空隙,且dmin=10 mm,颗粒间的空隙缺少充足的小颗粒去填充,所以在压实度较高的情况下仍有较大孔隙率。
由图4(a),不考虑颗粒破碎时,由于制样较为密实,不同围压下均表现出应变软化现象,围压越大应变软化越明显;同一围压下不同缩尺试样的峰值偏应力差别较小;到达峰值偏应力后,各缩尺试样的应力–应变曲线基本重合。以上结果与Sitharam等[39]的一致,即不考虑颗粒破碎且级配平行试样的宏观力学响应基本相同。由图4(b),考虑颗粒破碎时,各缩尺试样的力学响应呈现较为明显的差异,围压越大差异越明显,但均表现为最大粒径越大的试样其峰值偏应力越小;试样的应变软化程度减弱,甚至出现应变硬化现象。当颗粒更易破碎时(图4(c),
σ0 =140 MPa),试样间应力–应变曲线的差异进一步增大。马刚等[24]和Ovalle等[22]指出颗粒破碎是试样抗剪强度随试样尺寸增加而降低的主要原因之一;相同试验围压时,尺寸越大(最大粒径越大)的试样,颗粒破碎率越高。此处使用Marsal[3]提出的马萨尔破碎率Bm计算各组缩尺试样的颗粒破碎率,如图5所示。可知,试验围压越大时,试样的颗粒破碎率越高;同一试验围压下,最大粒径越大的试样其颗粒破碎率越大;相同试验围压下的同尺寸初始试样,颗粒特征破碎强度越小,则试样的颗粒破碎率越大。以上规律重现了文献[4,22]室内试验观察到的结果,表明研究中开展的数值模拟试验是合理可行的。
3.2 颗粒破碎对试样孔隙率的影响
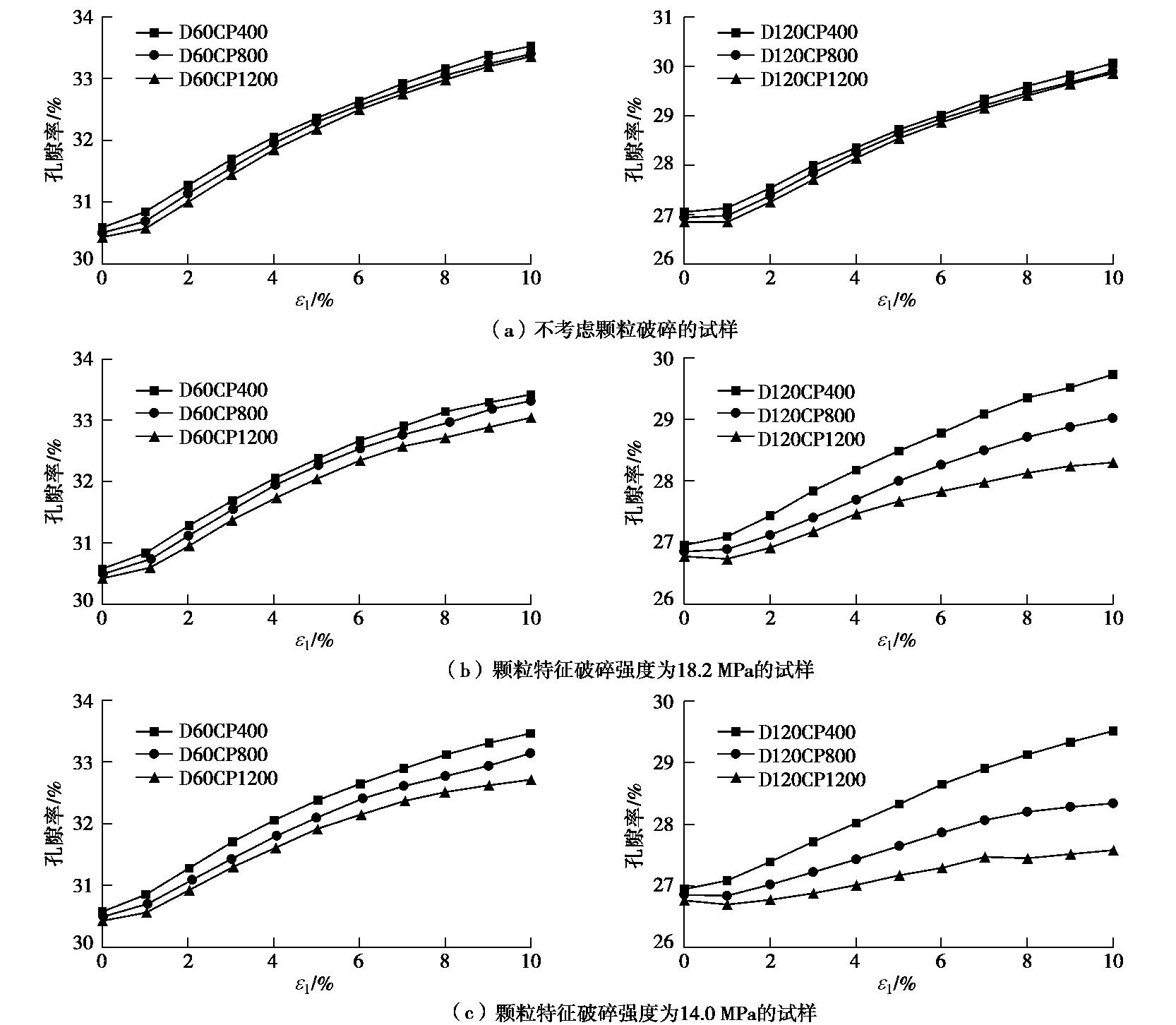
试样孔隙率是描述试样密实程度的重要指标。各组缩尺试样孔隙率的演化曲线如图6所示。不同尺寸试样孔隙率的演化规律相似,此处仅给出最大颗粒粒径为60,120 mm试样的孔隙率演化曲线。
如图6(a)所示,不考虑颗粒破碎时,不同尺寸试样的孔隙率在不同围压下的演化曲线近乎平行,基本保持剪切开始时孔隙率的差异水平。考虑颗粒破碎时(图6(b)),由于不同试验围压下试样颗粒的破碎率有差异,且随试验的进行差异逐渐增加,所以表现出不同试验围压下试样孔隙率间的差异随剪切逐渐增加现象;且由于小尺寸试样破碎率低于大尺寸试样,因此表现出小尺寸试样的这种差异增加不大,大尺寸试样的这种差异增加明显;当颗粒更易破碎时(图6(c)),这一差异更为明显。
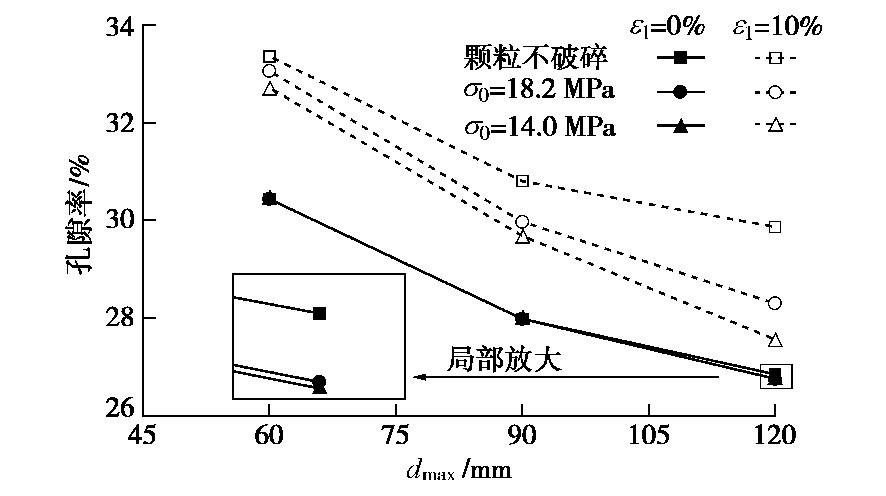
为直观对比剪切前后试样孔隙率的变化,提取1.2 MPa试验围压下的各缩尺试样在轴向应变为0%(剪切前)和10%(剪切后)时的孔隙率如图7所示。可知,剪切前各组缩尺试样孔隙率差别很小;但由于颗粒破碎的影响,考虑颗粒破碎试样的孔隙率略小于不考虑颗粒破碎的试样,如局部放大图所示,这与初始试样施加至目标围压时发生的少量颗粒破碎有关。剪切后,由于颗粒破碎的影响,不同缩尺试样组中相同尺寸试样的孔隙率呈现出明显的差异;根据各缩尺试样破碎率与颗粒最大粒径的关系(图5),图7总体表现为颗粒破碎率越大的试样,剪切后试样的孔隙率越小。以上结果表明,颗粒破碎对堆石料缩尺试样孔隙率及其演化有明显的影响,剪切过程中颗粒的破碎加剧了不同尺寸试样孔隙率的差异程度,主要表现为最大颗粒粒径越大的试样,其孔隙率越小,试样越密实;颗粒越易破碎,该趋势越明显。
3.3 颗粒破碎对试样有效孔隙率的影响
试样的孔隙率描述了堆石料的密实度,然而试样中有一些小颗粒填充于大颗粒间形成的空隙中,不起承载外力的作用,因此试样孔隙率并不能描述试样中具有承力作用颗粒的占比。根据Thornton[40]的定义,本研究取颗粒接触数目小于2的颗粒为只起填充作用而不承载外力的颗粒,并定义这种颗粒为悬浮颗粒,则试样有效孔隙率
neff 定义为neff=(1−Vs−VfVtot)×100%, (4) 式中,
Vtot 为试样体积,Vs 为试样中颗粒的体积,Vf 为试样中悬浮颗粒的体积。此外,定义悬浮颗粒体积分数φf=(Vf/Vs)×100% 。最大颗粒粒径为60,90,120 mm的初始试样中悬浮颗粒体积分数分别为12.77%,20.75%和24.37%,悬浮颗粒体积分数随颗粒最大粒径的增大而增加,表明最大颗粒粒径越大,试样的骨架效应越明显。这与董槐三等[16]的研究结论一致,并指出这与试样堆积结构有关,即粒径越大时,颗粒间的空隙越大,小颗粒填充在其中处于悬浮状态可能性更大,从而大尺寸试样表现出更强的骨架效应。
各组缩尺试样的有效孔隙率随试样剪切的演化曲线如图8所示。不同尺寸试样有效孔隙率的演化规律相似,此处仅给出最大颗粒粒径为60,120 mm试样的有效孔隙率演化曲线。对于小尺寸试样(如图8(a),(b),(c)左图),不考虑颗粒破碎且
ε1 ≤1%时,有效孔隙率发生较为明显的下降(图8(a)左图),即悬浮颗粒占比减少;考虑颗粒破碎且ε1 ≤1%时,有效孔隙率没有降低(图8(b),(c)左图,0.4和0.8 MPa),表明在剪切初期,颗粒破碎产生的碎片大多成为无效填充颗粒,抵消了原本的下降趋势;而图8(b),(c)左图中1.2 MPa试验围压时,有效孔隙率随剪切有略微下降,表明破碎率的升高(围压越大,破碎率越大)使颗粒间空隙中逐渐充满碎片小颗粒,使之从无效填充颗粒向有效填充颗粒转变。对于大尺寸试样(如图8(a),(b),(c)右图),不考虑颗粒破碎且
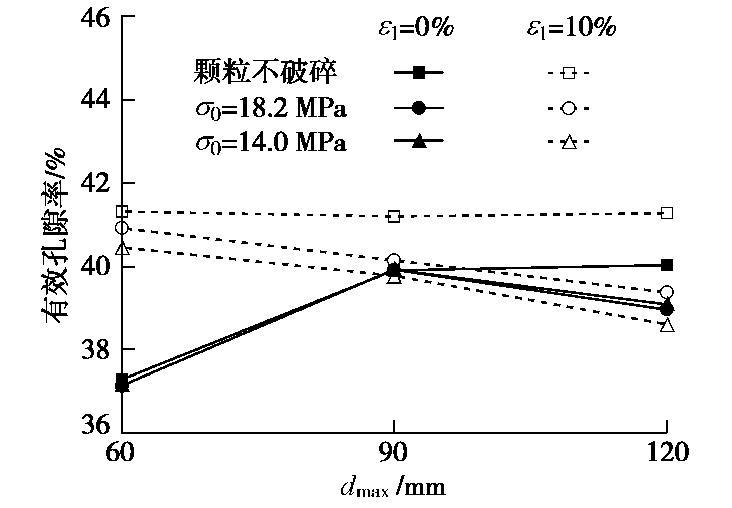
ε1 ≤1%时,有效孔隙率显著降低;考虑颗粒破碎且ε1 ≤2%时,试样有效孔隙率持续降低,即颗粒破碎推迟了有效孔隙率发生转变的时机(图8(b),(c)右图与图8(a)右图相比),这个阶段试样的承力结构逐渐密实;之后,由于不同围压下试样的颗粒破碎率有差异,围压越大的试样其破碎率越高,产生的有效填充颗粒占比也越高,试样的有效孔隙率越小,最终不同围压下试样(图8(b),(c)右图)的有效孔隙率未发生如图8(a)右图中的聚集现象。以上结果表明,颗粒破碎影响了剪切过程中试样承力结构的演化,颗粒越易破碎则剪切后试样的有效孔隙率越小,也即承力结构越密集,且尺寸越大试样受到的影响越明显;此外,剪切后有效孔隙率随试样尺寸增大而减小(图9),与剪切前的规律相反;以上规律,不同于图7中所呈现的剪切前与剪切后孔隙率随尺寸变化一致的规律。
3.4 颗粒破碎对试样配位数的影响
颗粒配位数是指目标颗粒与周边颗粒发生接触的数目,是反映颗粒集合体内部结构特征的重要参数之一[41-42]。为了进一步理清颗粒破碎对堆石料缩尺试样填充特性的影响,本节分别对各组缩尺试样的有效配位数和配位数频率分布的演化进行分析。
(1)试样有效配位数
本研究中采用Thornton[40]对有效配位数的定义,即除去试样中颗粒配位数小于2的悬浮颗粒后试样的平均配位数为试样有效配位数
CNeff ,CNeff=2C−N1Ntot−N1−N0, (5) 式中,C为试样中的接触总数,
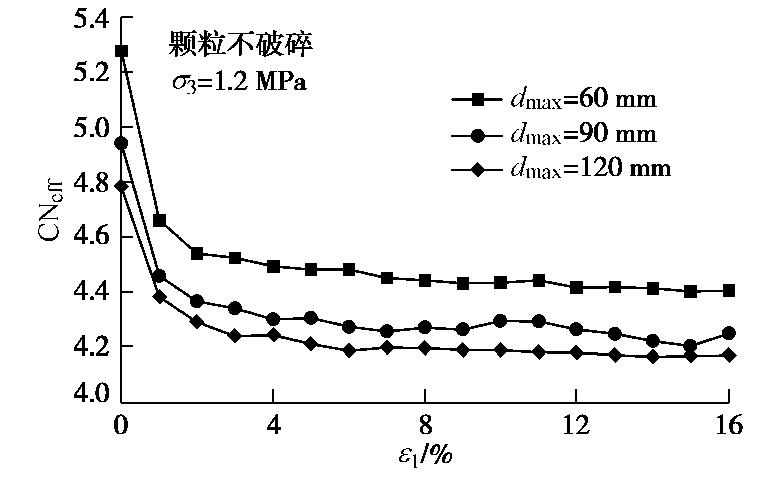
Ntot ,N0 和N1 分别为试样中颗粒的总数、配位数为0的颗粒数目和配位数为1的颗粒数目。各围压下考虑和不考虑颗粒破碎试样有效配位数演化表现出相似的规律,此处仅给出1.2 MPa试验围压下不考虑颗粒破碎试样有效配位数随剪切演化的曲线如图10所示。可知,不同尺寸试样有效配位数随剪切演化的规律相似,均表现出先陡降后缓慢降低直至稳定的规律,这与文献[43]的研究结果一致。不同尺寸试样的有效配位数有明显差异,最大颗粒粒径越大试样的有效配位数越低,表明尺寸越大的试样在剪切过程中的承力结构越稀疏。
(2)配位数频率分布
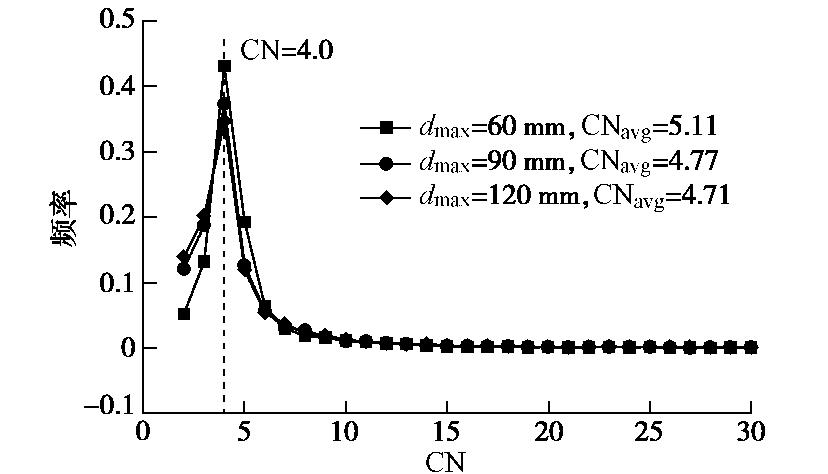
配位数频率分布是衡量试样结构特征的另一重要参数,本节中配位数频率分布均指除去悬浮颗粒后的。初始试样配位数频率分布如图11所示。
可知,不同尺寸试样的配位数频率分布曲线相似,但数值上存在较为明显的差异。不同尺寸的初始试样中,配位数为4的颗粒的频率均是最大值,在峰值左侧试样尺寸越大则频率越高,在峰值右侧试样尺寸越大则频率越低,最终dmax为60,90,120 mm试样的有效平均配位数分别为5.11,4.77,4.71,以上表明,尺寸越大试样的承力结构越不紧密,这可认为是由于级配越宽的试样中大颗粒间形成的空隙更大,填充其中的小颗粒没有成为稳定受力结构的一部分导致的。
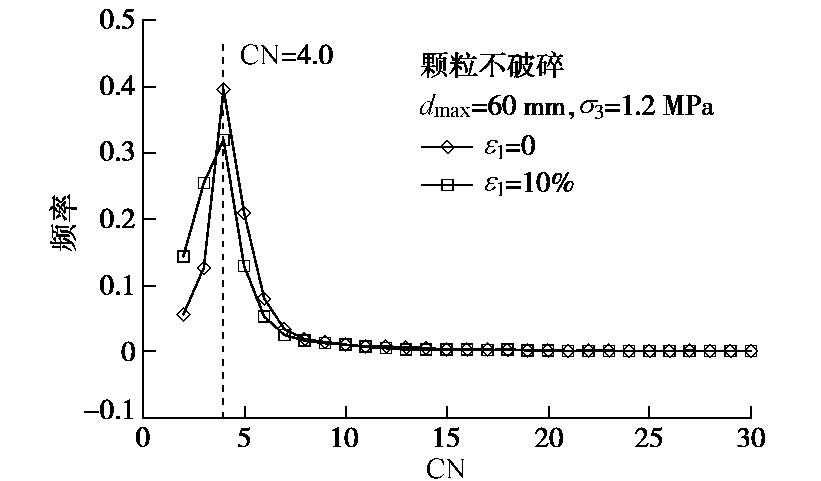
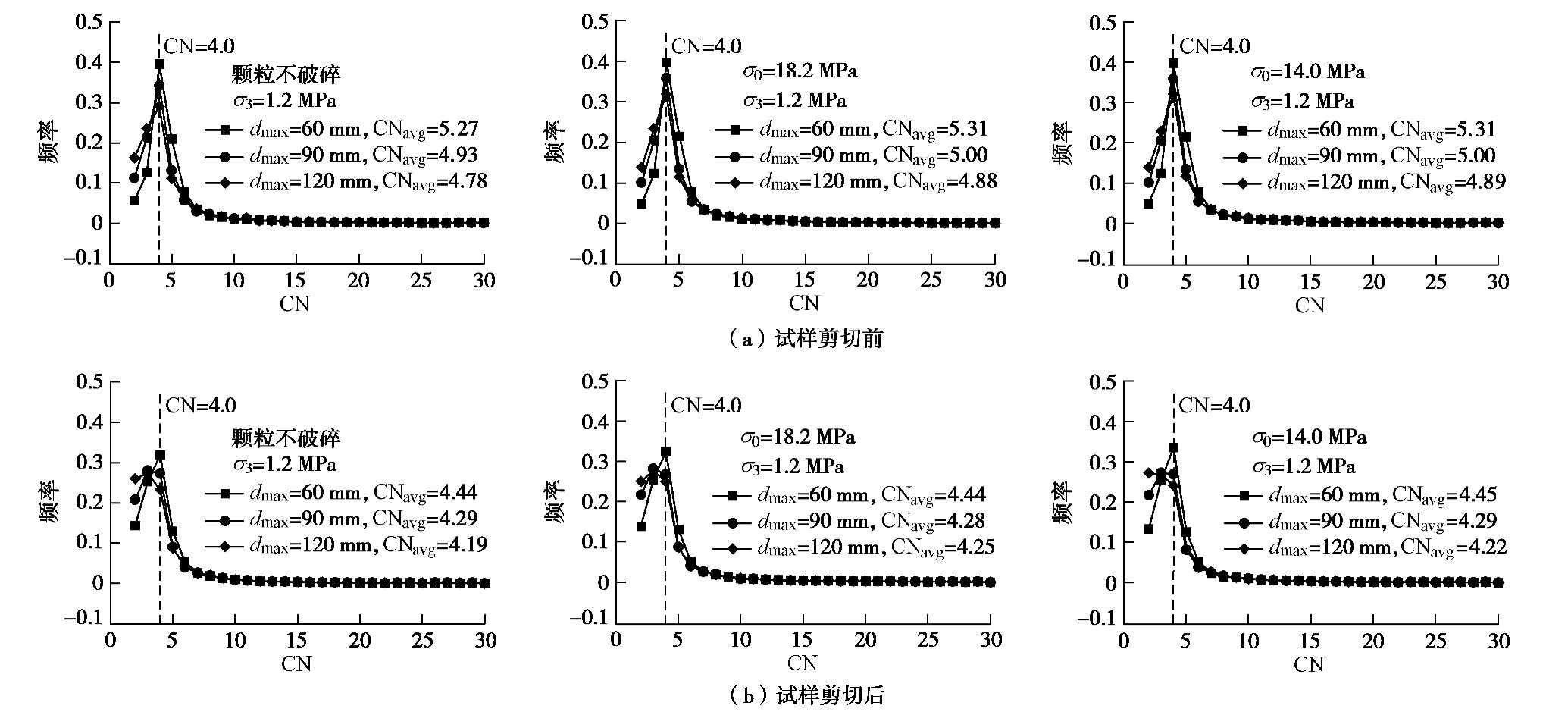
图12为不考虑颗粒破碎且dmax= 60mm的试样在1.2 MPa试验围压下剪切前后配位数频率分布对比图。可知,剪切试验后,峰值有所下降,配位数频率分布曲线CN=4.0左侧上抬,右侧下降;试样有效平均配位数也由剪切前的5.27降低到剪切后的4.44。以上现象是由于试样的剪胀引起的,当试样发生剪胀时,颗粒间原本密实的排列变疏松,会导致颗粒配位数降低,进而引起试样有效平均配位数降低。其他围压下的缩尺试样在剪切前后均有相似规律,此处不列出。
图13为1.2 MPa试验围压下各组缩尺试样剪切前(
ε1 =0%)和剪切后(ε1 =10%)试样配位数频率分布图。可知,各组缩尺试样剪切前后的配位数频率分布呈现相似的分布规律。剪切前,试样配位数频率分布规律类似初始状态时的分布情况;剪切后,CN=4.0左侧表现为试样尺寸越大频率越高,CN=4.0右侧差异不明显,但仍表现为试样尺寸越大,频率越低的规律。由图13(b)可知,试样的剪胀增加了小配位数(CN<4.0)颗粒占比,而颗粒的破碎加剧了这一现象,破碎率越高的大尺寸试样中,小配位数颗粒占比增加的幅度越大。颗粒集合体中,配位数越少的颗粒在力学上越不易稳定。因而,除了从颗粒破碎时承力结构的失效与结构调整解释堆石料力学响应的差异外,各缩尺试样剪切过程中有效配位数演化的差异也应是其力学响应间差异的原因之一,即大尺寸试样较小尺寸试样在剪切过程中产生了更多的力学不稳定颗粒,试样承载外力时,这些力学不稳定颗粒更易发生调整(如失稳、滚动等),使试样的承载能力降低,从而表现出堆石料大尺寸试样的峰值抗剪强度小于堆石料小尺寸试样的峰值抗剪强度。
4. 结论
本文基于离散元方法,采用碎片替代方法(FRM)模拟颗粒的破碎,并考虑颗粒破碎强度的尺寸效应及Weibull分布特性,从宏、细观尺度开展了颗粒破碎对堆石料填充特性缩尺效应的影响研究。
(1)基于离散元法的数值模拟试验重现了室内试验观察到的现象,并与已有的研究结论相符,表明研究中开展的数值模拟试验是合理可行的。
(2)颗粒越易破碎,各缩尺试样的力学响应差异越大,堆石料缩尺效应越明显;尺寸越大的试样,剪切前、后的孔隙率均越小,颗粒越易破碎该趋势越明显。
(3)试样尺寸越大则骨架效应越强,颗粒越易破碎时剪切后的有效孔隙率越小,且大试样尺寸更易受到影响;剪切前试样的有效孔隙率随试样尺寸增大而增大,这一规律与剪切后的规律相反。
(4)不同尺寸试样的有效配位数随剪切均表现出先陡降后缓慢降低直至稳定的规律,尺寸越大试样的有效配位数越低;剪切过程中,大尺寸试样较小尺寸试样产生了更多的力学不稳定颗粒,这是造成堆石料缩尺效应的原因之一。
-
-
[1] BURLAND J B. On the compressibility and shear strength of natural clays[J]. Géotechnique, 1990, 40(3): 329-378. doi: 10.1680/geot.1990.40.3.329
[2] LEROUEIL S, VAUGHAN P R. The general and congruent effects of structure in natural soils and weak rocks[J]. Géotechnique, 1990, 40(3): 467-488. doi: 10.1680/geot.1990.40.3.467
[3] DAFALIAS Y F, POPOV E P. A model of nonlinearly hardening materials for complex loading[J]. Acta Mechanica, 1975, 21(3): 173-192. doi: 10.1007/BF01181053
[4] HASHIGUCHI K. Subloading surface model in unconventional plasticity[J]. International Journal of Solids and Structures, 1989, 25(8): 917-945. doi: 10.1016/0020-7683(89)90038-3
[5] YAO Y P, HOU W, ZHOU A N. UH model: three-dimensional unified hardening model for overconsolidated clays[J]. Géotechnique, 2009, 59(5): 451-469. doi: 10.1680/geot.2007.00029
[6] NOVA R, CASTELLANZA R, TAMAGNINI C. A constitutive model for bonded geomaterials subject to mechanical and/or chemical degradation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(9): 705-732. doi: 10.1002/nag.294
[7] ASAOKA A, NAKANO M, NODA T. Superloading yield surface concept for highly structured soil behavior[J]. Soils and Foundations, 2000,40(2): 99-110. doi: 10.3208/sandf.40.2_99
[8] DESAI C S, TOTH J. Disturbed state constitutive modeling based on stress-strain and nondestructive behavior[J]. International Journal of Solids and Structures, 1996, 33(11): 1619-1650. doi: 10.1016/0020-7683(95)00115-8
[9] 沈珠江. 结构性黏土的弹塑性损伤模型[J]. 岩土工程学报, 1993, 15(3): 21-28. doi: 10.3321/j.issn:1000-4548.1993.03.003 SHEN Zhu-jiang. An elasto-plastic damage model for cemented clays[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(3): 21-28. (in Chinese) doi: 10.3321/j.issn:1000-4548.1993.03.003
[10] JIANG M J, ZHANG F G, SUN Y G. An evaluation on the degradation evolutions in three constitutive models for bonded geomaterials by DEM analyses[J]. Computers and Geotechnics, 2014, 57: 1-16. doi: 10.1016/j.compgeo.2013.12.008
[11] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. doi: 10.1680/geot.1979.29.1.47
[12] 蒋明镜, 刘静德, 孙渝刚. 基于微观破损规律的结构性土本构模型[J]. 岩土工程学报, 2013, 35(6): 1134-1139. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201306022.htm JIANG Ming-jing, LIU Jing-de, SUN Yu-gang. Constitutive model for structured soils based on microscopic damage law[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1134-1139. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201306022.htm
[13] 蒋明镜. 现代土力学研究的新视野—宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019,41(2): 195-254. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[14] JIANG M J, SHEN Z F, WANG J F. A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances[J]. Computers and Geotechnics, 2015, 65: 147-163. doi: 10.1016/j.compgeo.2014.12.011
[15] 蒋明镜, 孙若晗, 李涛, 等. 一个非饱和结构性黄土三维胶结接触模型[J]. 岩土工程学报, 2019, 41(S2): 213-216. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S1055.htm JIANG Ming-jing, SUN Ruo-han, LI Tao, et al. A three-dimensional cementation contact model for unsaturated structural loess[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 213-216. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S1055.htm
[16] ITASCA Consulting Group. Inc. Manual of partied flow code version 5.0[M]. 2014.
[17] SHEN Z F, JIANG M J, WAN R. Numerical study of inter- particle bond failure by 3D discrete element method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(4): 523-545. doi: 10.1002/nag.2414
[18] JIANG M J, KONRAD J M, LEROUEIL S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(7): 579-597. doi: 10.1016/S0266-352X(03)00064-8
[19] YU A B. Discrete element method: an effective way for particle scale research of particulate matter[J]. Engineering Computations, 2004, 21(2/3/4): 205-214.
[20] 胡再强. 黄土结构性模型及黄土渠道的浸水变形试验与数值分析[D]. 西安: 西安理工大学, 2000. HU Zai-qiang. Inundation Deformation Test and Numerical Analysis on Loess Structural Model and Loess Canal[D]. Xi'an: Xi'an University of Technology, 2000. (in Chinese)
[21] MACCARINI M. Laboratory Studies of Weakly Bonded Artificial Soil[D]. London: University of London, 1987.
[22] 张鹏. 非饱和黄土力学特性与剪切带的真三轴试验及离散元模拟研究[D]. 上海: 同济大学, 2018. ZHANG Peng. True Triaxial Experimental and DEM Analysis of the Mechanical Properties and Shear Band of Unsaturated loess[D]. Shanghai: Tongji University, 2018. (in Chinese)
[23] REDDY K R, SAXENA S K. Effects of cementation on stress-train and strength characteristics of sands[J]. Soils and Foundations, 1993, 33(4): 121-134.
[24] MEHRABADI M M, NEMAT-NASSER S, ODA M. On statistical description of stress and fabric in granular materials[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1982, 6(1): 95-108.
[25] BAGI K. Stress and strain in granular assemblies[J]. Mechanics of Materials, 1996, 22(3): 165-177.
-
期刊类型引用(4)
1. 勒治华,于庆磊,蒲江涌. 充填散体材料侧限压缩试验径径比的确定方法. 中南大学学报(自然科学版). 2023(03): 1054-1061 .  百度学术
百度学术
2. 宋飞,朱婕,付娆. 考虑蠕变变形的格室加筋土力学性质研究. 地下空间与工程学报. 2023(S1): 165-173 .  百度学术
百度学术
3. 付娆,宋飞. 格室加筋土等效强度计算方法对比研究. 地基处理. 2021(03): 188-194 .  百度学术
百度学术
4. 朱家宏. 勘察土工试验数据科学性及准确性的提升策略分析——以岩土工程为例. 冶金管理. 2021(17): 126-127 .  百度学术
百度学术
其他类型引用(4)



 下载:
下载: