基于微流控芯片技术的微生物加固可视化研究

何想; 马国梁; 汪杨; 赵常; 刘汉龙; 楚剑; 肖杨

doi:10.11779/CJGE202006003

基于微流控芯片技术的微生物加固可视化研究 English Version

何想^{1, 2,},
马国梁^{1, 2},
汪杨^{1, 2},
赵常^{1, 2},
刘汉龙^{1, 2, 3},
楚剑⁴,
肖杨^{1, 2, 3, ,}

1.
重庆大学土木工程学院,重庆　400045
2.
重庆大学山地城镇建设与新技术教育部重点实验室,重庆　400045
3.
库区环境地质灾害防治国家地方联合工程研究中心（重庆）,重庆　400045
4.
南洋理工大学土木与环境工程学院,新加坡　639789

基金项目:

国家自然科学基金项目 51922024

国家自然科学基金项目 41831282

重庆市研究生科研创新项目 CYB18035

中央高校基本科研业务经费 2019CDQYTM031

详细信息

作者简介:
何想(1992—),男,博士研究生,主要从事微生物土加固机理方面的研究。E-mail: medihe@163.com

通讯作者:
肖杨, E-mail: hhuxyanson@163.com

中图分类号: TU43
计量
- 文章访问数: 589
- HTML全文浏览量: 21
- PDF下载量: 254
出版历程
- 收稿日期: 2019-11-03
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-05-31

Visualization investigation of bio-cementation process based on microfluidics

HE Xiang^{1, 2,},
MA Guo-liang^{1, 2},
WANG Yang^{1, 2},
ZHAO Chang^{1, 2},
LIU Han-long^{1, 2, 3},
CHU Jian⁴,
XIAO Yang^{1, 2, 3, ,}

1.
School of Civil Engineering, Chongqing University, Chongqing 400045, China
2.
Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Chongqing 400045, China
3.
National Joint Engineering Research Center of Geohazards Prevention in the Reservoir Areas (Chongqing), Chongqing 400045, China
4.
School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore

摘要

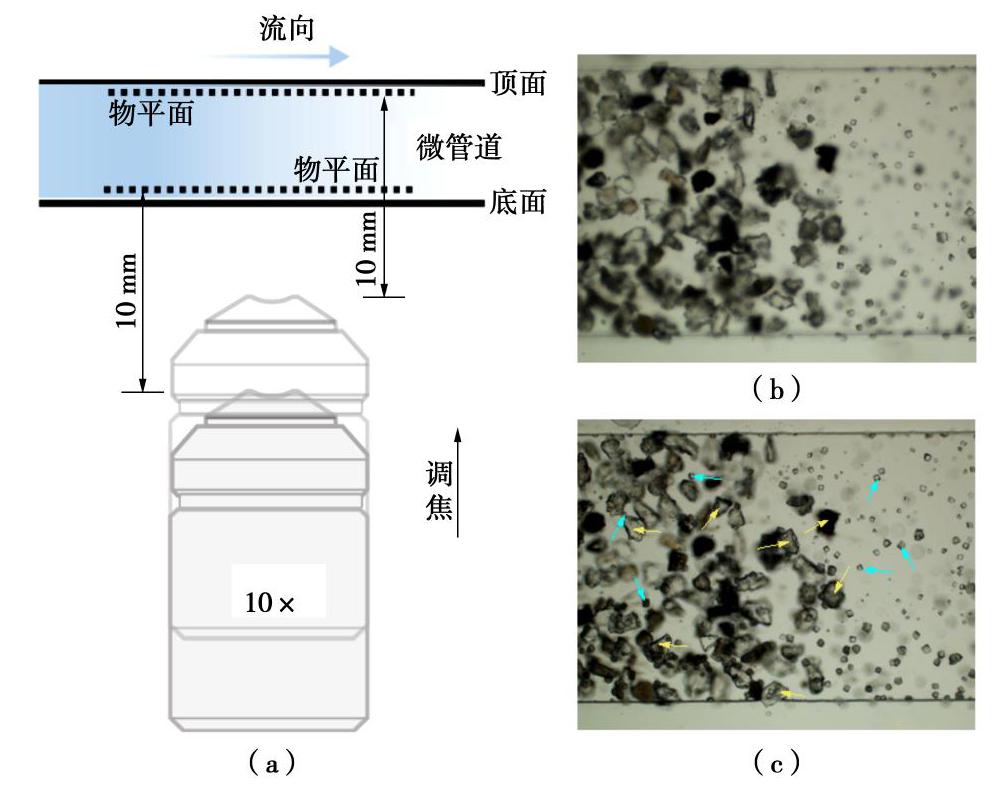
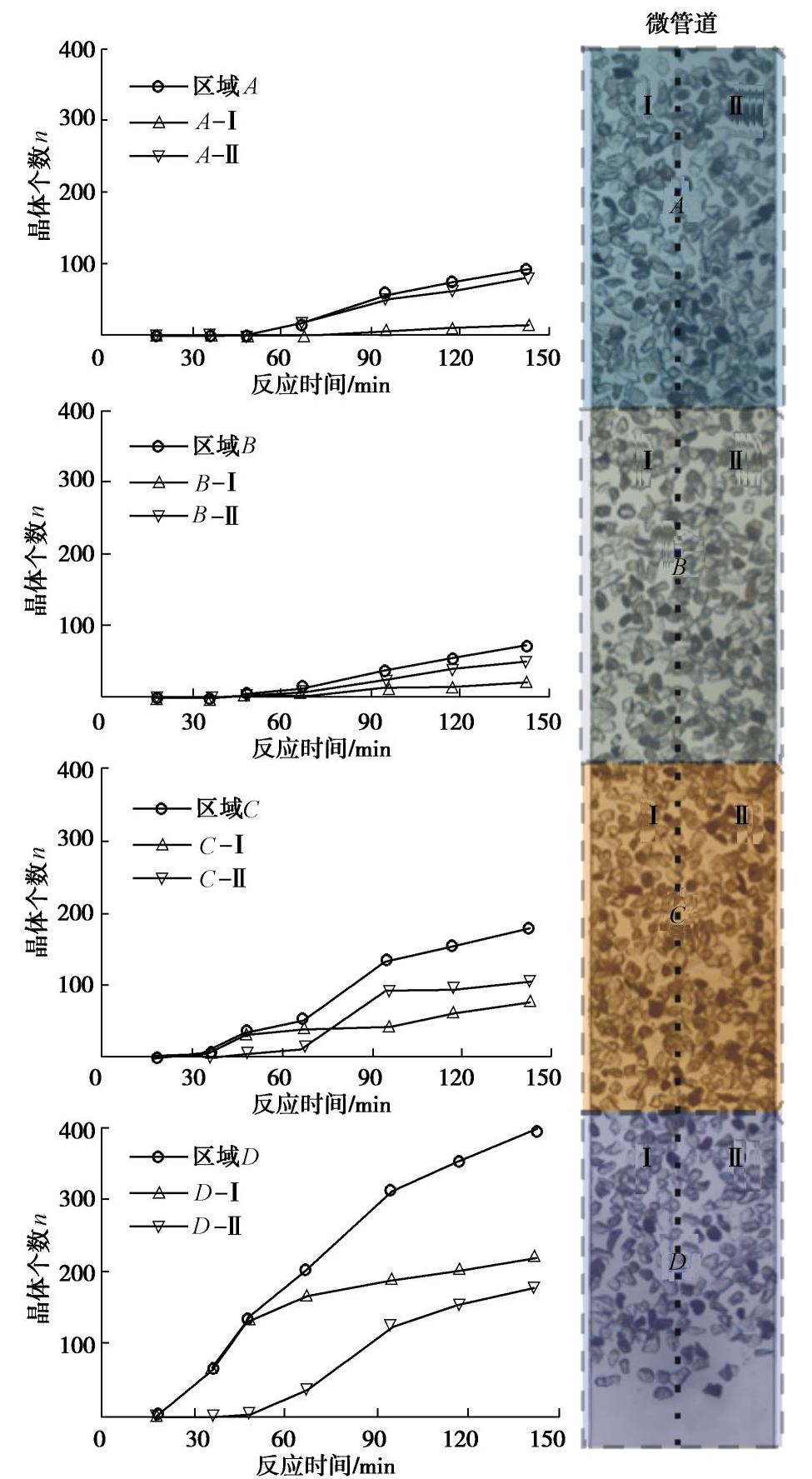
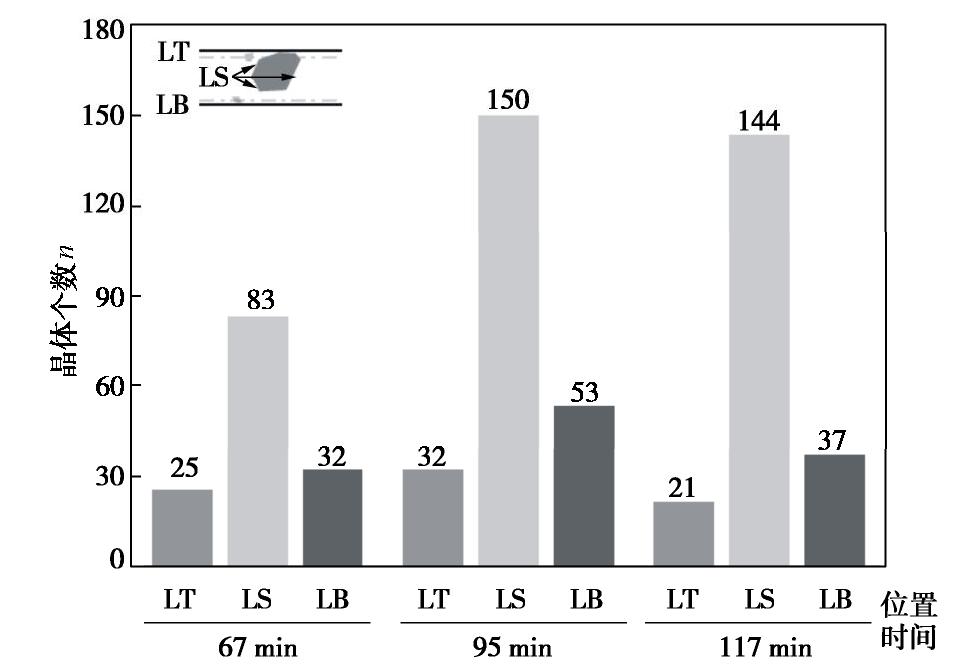
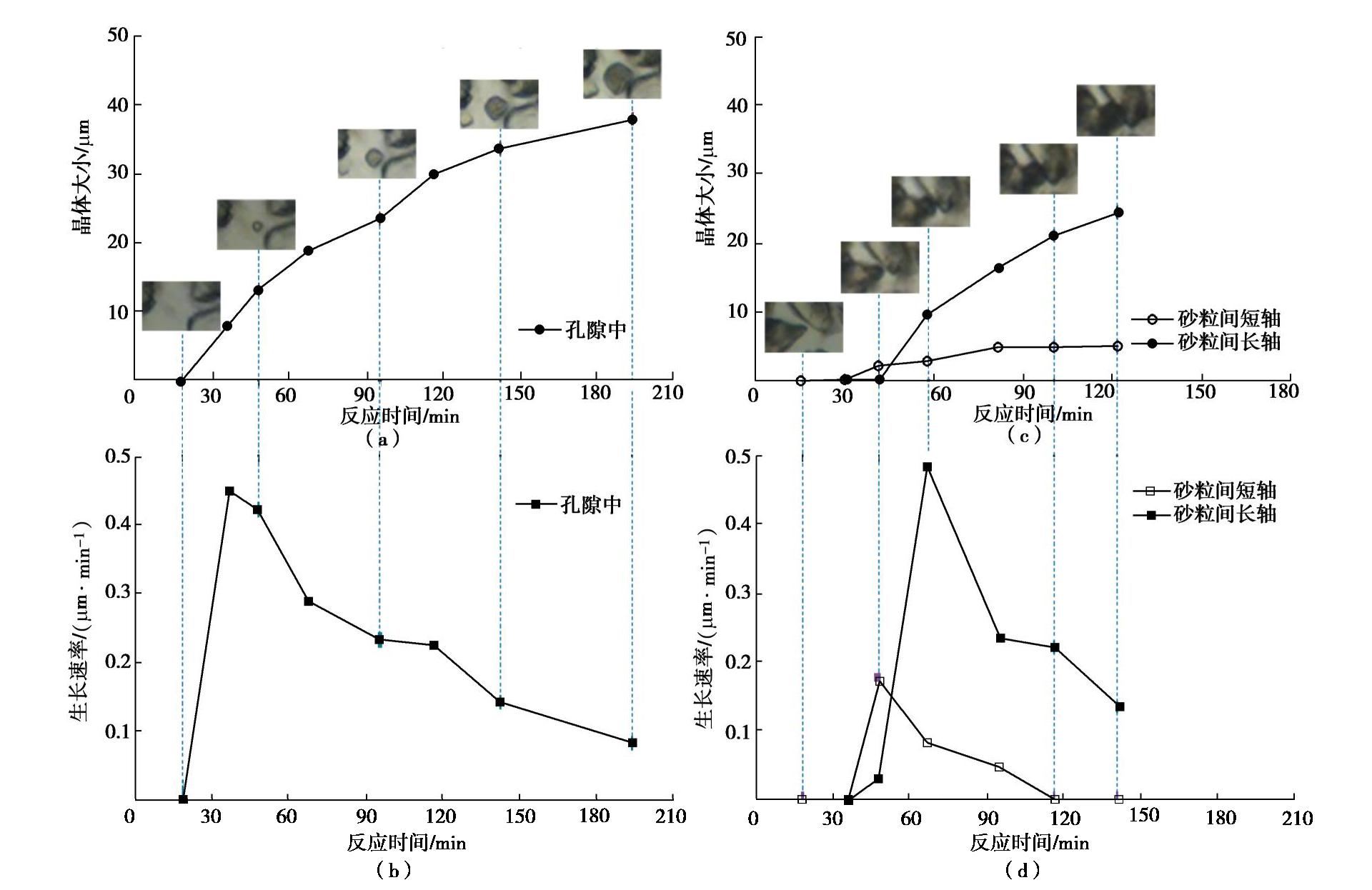
摘要: 微生物诱导碳酸钙沉积（MICP）能够加固散粒土体,是岩土工程中新兴绿色加固技术之一。然而,关于微生物加固机理以及矿化形成过程的研究尚不多见。基于微流控芯片技术开发了微生物加固可视化系统,利用该系统开展了微生物诱导碳酸钙矿化机理的原位微细观研究,通过对微生物加固过程中碳酸钙晶体的沉积进行了观测,并对其时空分布、沉积模式、生长速率进行了量化。结果表明溶质分子的对流和扩散作用对碳酸钙晶体分布影响较大,碳酸钙的分布存在时间不均匀和空间不均匀现象,时间不均匀随反应进行呈现弱化现象而空间不均匀在整个反应过程（0～2200 min）中一直存在。研究发现微尺寸管道中碳酸钙存在孔隙中和颗粒间两种沉积模式,孔隙中的碳酸钙均匀长大,而颗粒间碳酸钙存在不同速率的生长轴。研究结果将加深对微生物加固机理的认识,为微生物加固技术的优化和推广应用提供参考。
- 微生物矿化 /
- 微流控芯片 /
- 可视化 /
- 结晶 /
- MICP
Abstract: Biomineralization possesses the capability to bind granular materials, which can be used in the applications of geotechnical engineering as an emerging green ground improvement technology. However, little information is available on the mechanics of biomineralization, especially on the process of biocementation. An optical platform is proposed to visualize the process of biomineralization based on microfluidics. A series of micro-scale investigations related to this process are performed to capture the spatial distribution of calcium carbonate crystals, precipitation patterns and quantitative crystal growth rate. The results show that the convection and diffusion of solvent have significant impacts on the distribution of calcium carbonate, which demonstrates a nonuniform spatiotemporal distribution. The extent of uneven distribution in time scale is reduced as the reaction goes on. However, the phenomenon of uneven distribution in spatial scale is maintained during the whole reaction period (0~2200 min). Two precipitation patterns in biocementation are found in this study, i.e., precipitation at pore and precipitation at sand contacts. The precipitation at pore shows no growth axis, while the precipitation at sand contacts shows growth axis with different growth rates. These investigations may provide new insights into the mechanisms of microbial induced carbonate precipitation and are beneficial for the optimized design of up-scale application.
- biomineralization /
- microfluidics /
- visualization /
- crystallization /
- MICP

HTML全文

0. 引言

改革开放以来,交通基础设施建设呈现了井喷式发展,但部分地区由于受复杂地形、特殊地质、桥隧衔接以及路线总体线性要求等因素的影响,连拱结构形式被公路隧道所广泛采用。而其中的非对称连拱隧道除具有连拱隧道整体开挖跨度大,结构复杂和施工难度高等基本特征外,其结构形式及围岩受力特点相较于对称连拱隧道更为复杂,这使得确定合理的支护结构设计和隧道施工歩序变得更加困难,而目前尚无相应的设计、施工技术规范和标准可循,在建成并投入使用的工程案例也较为少见。因此,非对称连拱隧道一出现便成为隧道学界研究的热点问题。

周玉宏等^[1]、朱合华等^[2]、邓建等^[3]、王凯等^[4]、郑宗溪等^[5]、王亚琼等^[6]分别利用有限元软件对马宅顶隧道、青岛胶州湾海底隧道、兰渝铁路新作坊隧道、青海药水峡隧道、云南桥头隧道施工过程进行了数值模拟,获得了非对称连拱隧道不同开挖工序时围岩和支护结构的力学响应；高峰等^[7]则采用荷载–结构法对厦门市东坪山地下立交工程非对称连拱隧道的支护结构承载能力与正常使用极限状态进行验算。陈秋南^[8]、何珺等^[9]通过相似模型试验,分别研究了非对称连拱隧道开挖过程中左右硐室围岩应力、位移分布的基本规律和不同荷载条件下非对称连拱隧道的衬砌外表面压力和结构内力的分布及变化特点；王军等^[10]以福建罗长公路马宅顶工程为研究背景,通过对监测数据进行分析,探究了非对称连拱隧道开挖过程中的受力特点,为同类型工程的设计与施工提供了参考；陈洪涛等^[11]以西南地区某连拱隧道为工程依托,利用数值模拟重点分析了岩溶地层中连拱隧道不同埋深对围岩以及中隔墙的影响,进而推导了中隔墙适用长度的公式。上述研究一方面多是对非对称连拱隧道施工过程进行模拟,一方面则是利用监测数据对施工歩序进行调整,而目前针对非对称连拱隧道支护结构设计缺乏理论依据的问题并没有引起足够的重视。

围岩压力一直是隧道工程领域关注的重点,明确隧道围岩压力的作用模式和提供适用性强的围岩压力计算方法对支护结构设计至关重要^[12]。张俊儒等^[13] 利用相似模型试验,对非对称连拱隧道破坏形态进行研究,研究结果可以指导不等跨连拱隧道的设计与施工。朱正国等^[14]对压力拱的成因进行了分析,提出了压力拱内外边界的判定方法,利用参数敏感性分析和正交试验,拟合出围岩压力计算公式,并在此研究基础上进行拓展,将影响系数与简化公式相结合,推导出适用于连拱隧道的围岩压力计算公式。丁文其等^[15]利用三维有限元模型研究了分岔隧道荷载空间分布规律和围岩的破坏形式,在此基础上,提出了适用于分岔隧道围岩压力计算的空间荷载结构法,并通过与规范结果进行对比表明该方法计算结果符实际受力情况。针对非对称连拱隧道结构受力复杂、几何不规则、结构形式特殊等基本特征,李鹏飞等^[16]基于普氏平衡理论,结合公路隧道规范中关于深埋连拱隧道围岩压力的计算方法,提出了深埋条件下非对称连拱隧道的围岩压力计算公式,并结合马宅顶隧道围岩压力实测值对所推导公式的合理性进行了验证。综上所述,目前对于非对称连拱隧道围岩压力的研究多集中在状态设计方法层面,考虑施工过程影响的非对称连拱隧道过程荷载理论计算方法的研究较少。

1. 深埋单洞隧道普氏理论

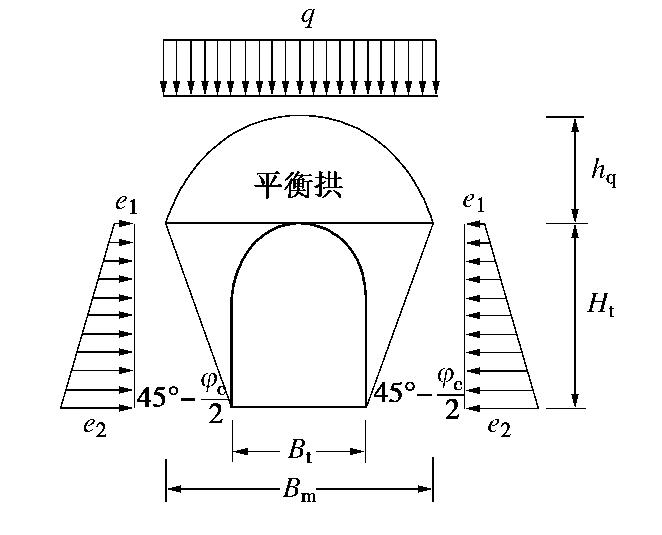
普氏公式是1907年проточьякунов（普罗托奇雅阔诺夫）基于天然拱概念提出的针对破碎岩体和松散地层的松动压力计算公式（图1）。根据普氏平衡拱理论的基本假设,深埋单洞隧道拱部竖向均布压力q和水平梯形分布压力e表示为

图 1 单洞隧道普氏理论示意图

Figure 1. Sketch map of Protodyakonov's theory for a single tunnel

下载: 全尺寸图片幻灯片

$q = γ h_{q}$ ,

(1)

$h_{q} = \frac{B_{m}}{2 f_{kp}}$ ,

(2)

$e_{1} = γ h_{q} \tan^{2} (45^{\circ} - \frac{φ_{c}}{2})$ ,

(3)

$e_{2} = γ (h_{q} + H_{t}) \tan^{2} (45^{\circ} - \frac{φ_{c}}{2})$ ,

(4)

$B_{m} = B_{t} + 2 H_{t} \tan^{2} (45^{\circ} - \frac{φ_{c}}{2})$ 。

(5)

式中 $γ$ 为围岩重度； $h_{q}$ 为天然拱高度； $B_{m}$ 为隧道平衡拱跨度； $f_{kp}$ 为岩石坚固系数,取 $f_{kp} = \tan φ$ , $φ$ 为围岩内摩擦角； $φ_{c}$ 为围岩计算摩擦角； $B_{t}$ 为隧道开挖跨度； $H_{t}$ 为隧道开挖高度。

2. 过程设计理念

曲海锋^[17]和朱合华等^[18]基于龙头山隧道、岚峰隧道的现场试验和数值分析结果,提出了大断面公路隧道过程设计方法的基本理念。过程设计方法的特点：根据隧道开挖歩序分析和计算设计荷载,考虑施工过程对隧道设计荷载的影响。

设计荷载产生的过程不同是过程设计理念与状态设计理念最本质的区别。过程设计方法考虑不同歩序之间荷载的影响,最终基于一定规则将计算荷载进行组合,从而得到作用于隧道整体结构上的松散压力。

根据文献[17],过程荷载计算方法的实现主要解决以下两个问题：

（1）对开挖步骤进行简化,获得合理的过程方法计算模型。

（2）如何考虑相邻开挖工序之间的影响程度。

2.1 简化模型的建立

（1）基本假设

对于深埋中小跨度隧道（开挖跨度B<14 m）,可以将过程荷载计算方法中的上下台阶开挖简化为一次开挖。文献[17]研究结果表明：当隧道（洞室）跨度小于15 m,且高跨比为1.0～1.5时,两种开挖方法引起的应力重分布相差不超过10%。公路隧道按其跨度分类^[19]如表1所示。

表 1 公路隧道按跨度分类表

Table 1. Classification of highway tunnels by span

分类	开挖跨度B/m	描述
小跨度隧道	B<9	①单车道公路隧道；②服务隧道；③人行横洞及车行横洞
中跨度隧道	9≤B<14	①双车道公路隧道；②单车道公路隧道的错车带
大跨度隧道	14≤B<18	①三车道公路隧道；②双车道公路隧道的紧急停车带
特大跨度隧道	B≥18	①四车道公路隧道（单洞）；②连拱隧道

下载: 导出CSV

| 显示表格

（2）过程荷载计算方法简化模型建立应遵循的两条原则

a）将整个隧道施工看作由多个平行导洞施工组成,考虑施工过程中不同工序之间的影响程度。

b）导洞的几何尺寸应符合实际开挖情况。

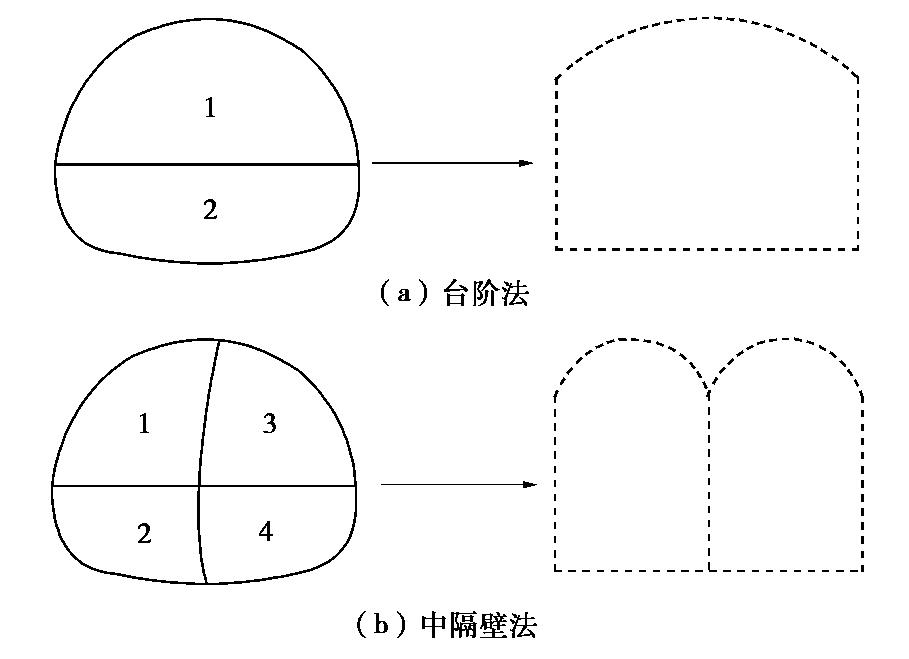
根据以上简化原则,台阶法、中隔壁法（CD、CRD法）简化模型如图2所示。图中数字代表施工工序,虚线为简化后各导洞位置。

图 2 开挖方法的简化模型

Figure 2. Simplified model for excavation method

下载: 全尺寸图片幻灯片

2.2 量化开挖工序的影响^[17]

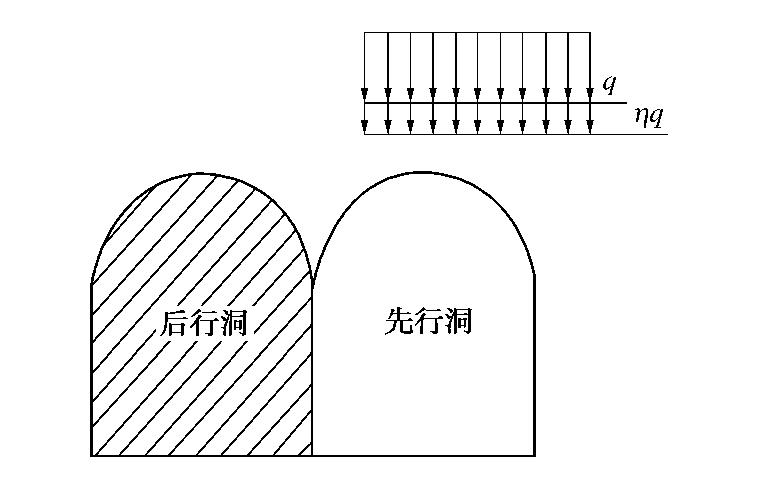
（1）影响系数 $η$ 通过引入影响系数 $η$ 来量化相邻开挖工序之间的影响程度。如图3所示,影响系数 $η$ 表示后行导洞开挖对先行导洞松动荷载的影响程度。

图 3 相邻导洞开挖荷载影响示意图^[17]

Figure 3. Sketch map of influence of excavation load on adjacent guide tunnels

下载: 全尺寸图片幻灯片

$η$ 取值的含义如下：

$η {\begin{matrix} > 1 \\ = 1 \end{matrix} \begin{matrix} \end{matrix} \begin{matrix} (后行洞开挖加剧了先行洞的松动荷载) \\ (两导洞之间相互独立) \end{matrix}$

。

文献[17]给出 $η$ 取值的具体表达式为

$\begin{matrix} η = {\begin{cases} \frac{β_{1} \cdot β_{2} \cdot β_{3}}{β_{4} \cdot β_{5}} (η \geq 1), \\ 1.0 (η < 1) 。 \end{cases} \end{matrix}$

(6)

式中, $β_{1}$ ～ $β_{5}$ 分别由导洞间距、后行洞几何形状、地质情况、先行洞支护参数和围岩等级确定。

以上5项影响指标的取值范围如表2所示。

表 2 影响指标的取值表^[17]

Table 2. Values of impact indices

导洞间距	0~0.2B	0.2B~0.4B	0.4~0.6B	0.6~0.8B	0.8B~1.0B	导洞间距	1.0B~1.2B	1.2B~1.4B	1.4B~1.6B	1.6B~1.8B	1.8B~2.0B	后行洞几何形状	高跨比>1.6	高跨比=1.2~1.6	高跨比=1.0~1.2	高跨比=0.6~1.0	高跨比<0.6	地质情况	包含上述3项因素	包含上述2项因素	包含上述1项因素	包含上述0项因素	先行洞支护情况	无支护	弱支护	普通支护	强支护	围岩等级	Ⅵ	Ⅴ	Ⅳ	Ⅲ以上
$β_{1}$ 取值	1.8	1.75	1.70~1.75	1.65~1.70	1.50~1.65	$β_{1}$ 取值	1.4~1.5	1.3~1.4	1.15~1.3	1.15~1.0	1.0	$β_{2}$ 取值	0.8	0.9	1.0	1.0~1.2	1.2~1.5	$β_{3}$ 取值	1.15	1.1	1.05	1.0	$β_{4}$ 取值	1.0	1.0~1.35	1.35	1.35~1.5	$β_{5}$ 取值	0.9	1.0	1.1	1.2
注：①B为后行洞的开挖跨度；② $β_{3}$ 考虑的3项因素为地表水、地下水和初始应力场。

下载: 导出CSV

| 显示表格

（2）权系数 $α$

权系数 $α$ 的含义为每个导洞引起的垂直均布荷载占隧道整体总荷载的大小,该系数小于1。权系数的计算公式为

$α_{i} = \frac{S_{i}}{S_{s}} = \frac{q_{i} \cdot b_{i}}{\sum_{i = 1}^{n} q_{i} \cdot b_{i}}$ ,

(7)

式中 $S_{i}$ 为单个导洞开挖引起的垂直荷载, $q_{i}$ 为单个导洞开挖引起的垂直均布荷载, $b_{i}$ 为单个导洞的开挖跨度, $S_{s}$ 为隧道垂直总荷载,n为导洞个数。

3. 深埋非对称连拱隧道过程荷载计算

非对称连拱隧道具有以下特点：

（1）隧道结构形式为非对称双连拱,结构受力复杂、偏压显著,不同于一般的单洞隧道。

（2）整体开挖跨度较大,非对称中开挖面积较小的隧道跨度多为8～12 m,而开挖面积较大的隧道跨度多为12～16 m。

（3）非对称连拱隧道施工过程中,左右隧洞开挖的非同步性会对围岩造成多次扰动。

（4）中隔墙为非对称连拱隧道受力体系中的关键部位,对整体结构稳定性起重要作用。

（5）支护结构多采用复合式衬砌。

在进行非对称连拱隧道围岩压力计算时,必须综合考虑以上特点。

3.1 连拱隧道围岩压力作用模式

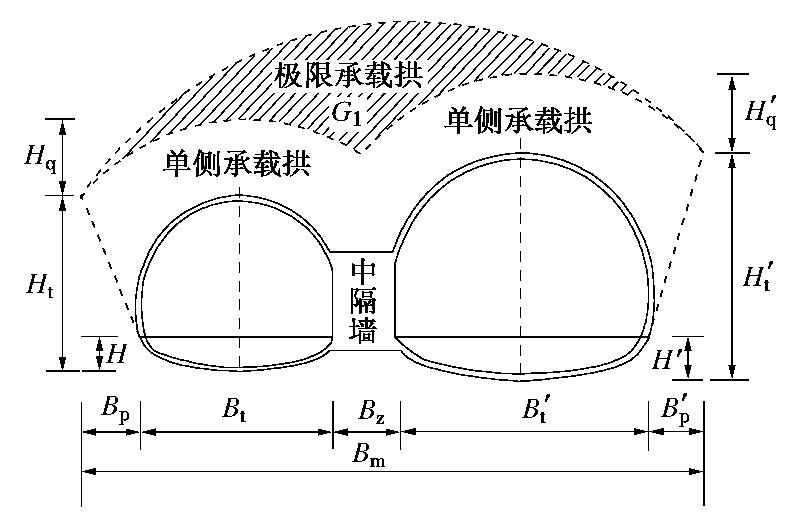
理论研究和工程实践表明,对于连拱隧道,中隔墙施工和浇筑效果及两侧导洞的开挖工序影响围岩压力的大小和平衡拱的形成。同时,中隔墙作为连拱隧道最关键的部位,其稳定性直接影响隧道围岩压力的作用模式。深埋条件下,根据过程荷载计算方法和普氏理论假定可以认为连拱隧道平衡拱形成存在两种极端情况：中隔墙浇筑效果良好,左右洞室可以分别形成稳定的承载拱,左右洞室施工顺序影响单侧承载拱大小,先行洞松散荷载考虑后行洞开挖对先行洞松散荷载的加剧情况；当中隔墙顶部回填不密实,左右洞室将作为整体形成共同的承载拱,即仅考虑隧道开挖过程的影响,忽略中隔墙的支护作用,以整体隧道开挖跨度形成极限承载拱,如图4所示。

图 4 深埋非对称连拱隧道承载拱示意图

Figure 4. Diagram of load-carrying arch for deep-buried asymmetric multi-arch tunnels

下载: 全尺寸图片幻灯片

就一般情况而言,深埋连拱隧道围岩压力作用模式介于两种极端状态之间,即由于中隔墙的作用承担了部分极限承载拱下部松散岩土体压力,对极限承载拱的形成起到了抑制效果,因此,连拱隧道过程荷载为中隔墙顶部压力、拱部松散压力和开挖过程引起的附加压力之和。

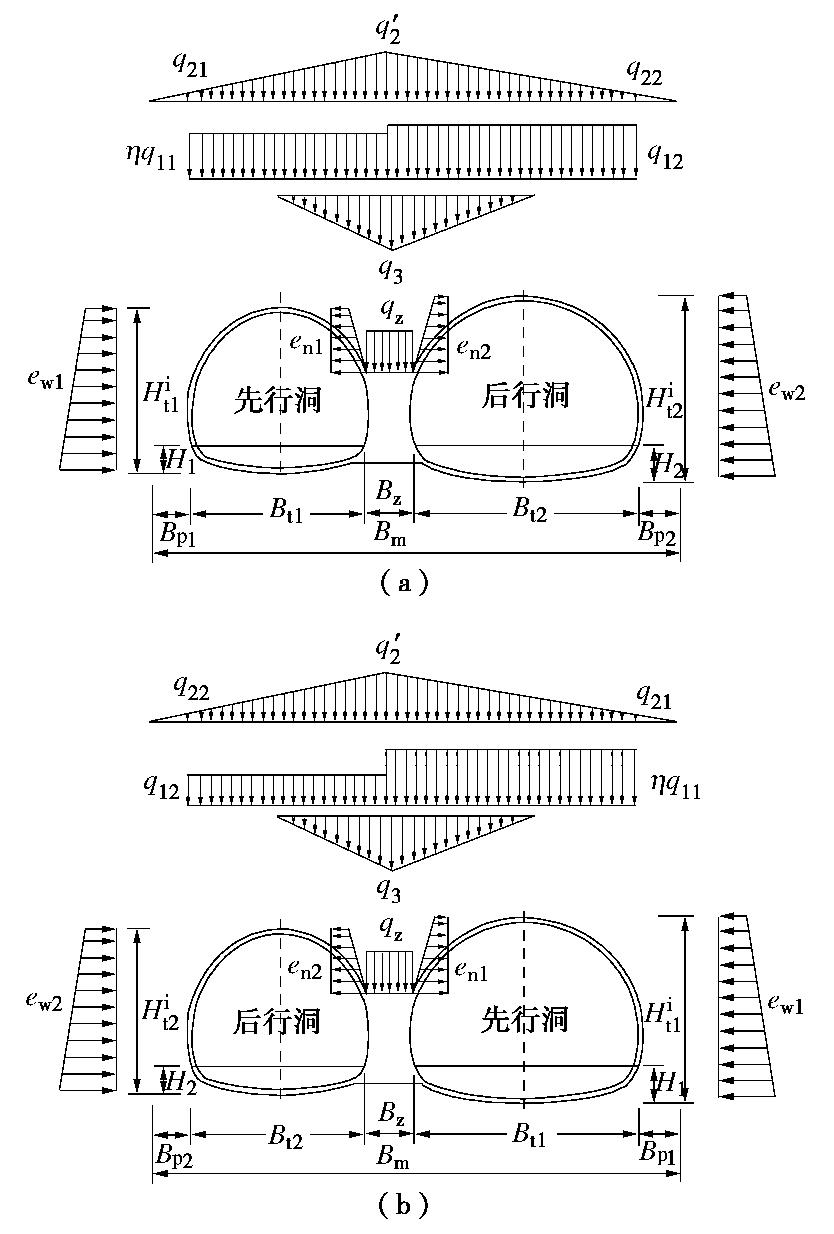
如图5所示,深埋非对称连拱隧道过程荷载包括以下部分^[19]：

图 5 深埋非对称连拱隧道荷载分布

Figure 5. Load distribution of deep-buried asymmetric multi-arch tunnels

下载: 全尺寸图片幻灯片

（1）拱部基本松散荷载 $q_{1}$ ,包括后行洞开挖对先行洞松散荷载加剧后先行洞形成稳定承载拱下部的围岩压力 $η q_{11}$ 和后行洞形成稳定承载拱下部的围岩压力 $q_{12}$ ,假定两者的分布形式均为均布荷载。

（2）拱部附加松散荷载 $q_{2}$ ,即极限承载拱下部松散岩体减去基本松散岩体和中隔墙顶预支撑围岩压力后的荷载,假定为梯形分布荷载。包括极限承载拱内侧 ${q^{'}}_{2}$ 和极限承载拱外侧 $q_{21}$ , $q_{22}$ 。

（3）中隔墙顶松散围岩压力荷载 $q_{3}$ ,即中隔墙顶至左右洞拱顶之间松散岩体形成的分布荷载。

（4）中隔墙顶附加均布荷载 $q_{z}$ ,即由于中隔墙的预支撑作用产生的围岩压力荷载。

（5）非对称连拱隧道侧向压力可以分解为中隔墙两侧及衬砌两侧的水平压力。

3.2 计算过程中的基本假定

根据规范^[19],极限破裂面与基本破裂面均为抛物线,拱顶水平线与承载拱曲线围成的面积为

$S = \frac{2}{3} B H$ ,

(8)

式中, $H$ 为承载拱高度, $B$ 为承载拱跨度。

根据普氏原理和过程荷载计算方法,假定先行洞与后行洞的各导洞开挖时的平衡拱高度 $H_{q_{11}}^{i}$ 和 $H_{q_{12}}^{i}$ ,以及极限承载拱高度 $H_{m}$ 。

$H_{q_{11}}^{i} = \frac{1}{2 f_{kp}} [b_{t_{1}}^{i} + (H_{t_{1}}^{i} - H_{1}) \tan (45^{\circ} - \frac{φ_{c}}{2}) + \frac{1}{2} B_{z} \cdot \frac{b_{t_{1}}^{i}}{B_{t_{1}}}],$

(9)

$H_{q_{12}}^{i} = \frac{1}{2 f_{kp}} [b_{t_{2}}^{i} + (H_{t_{2}}^{i} - H_{2}) \tan (45^{\circ} - \frac{φ_{c}}{2}) + \frac{1}{2} B_{z} \cdot \frac{b_{t_{2}}^{i}}{B_{t_{2}}}],$

(10)

$H_{m} = \frac{B_{m}}{2 f_{kp}}$ 。

(11)

图中和式中 $\sum_{i = 1}^{n} (H_{t_{1}}^{i} - H_{1}) \tan (45^{\circ} - \frac{φ_{c}}{2}) = B_{p_{1}}$ ； $\sum_{i = 1}^{n} (H_{t_{2}}^{i} - H_{2}) \tan (45^{\circ} - \frac{φ_{c}}{2}) = B_{p_{2}}$ ； $\sum_{i = 1}^{n} b_{t_{1}}^{i} = B_{t_{1}} ； \sum_{i = 1}^{n} b_{t_{2}}^{i}$ $B_{t_{2}}$ ； $B_{m} = B_{t_{1}} + B_{t_{2}} + B_{z} + B_{p_{1}} + B_{p_{2}}$ ； $b_{t_{1}}^{i}$ , $b_{t_{2}}^{i}$ 分别为先行洞和后行洞对应导洞的几何宽度； $H_{t_{1}}^{i}$ , $H_{t_{2}}^{i}$ 分别为先行洞和后行洞对应导洞的几何高度； $B_{t_{1}}$ , $B_{t_{2}}$ 分别为先行洞和后行洞跨度； $B_{p_{1}}$ , $B_{p_{2}}$ 分别为先行洞和后行洞侧面破裂面在水平面上的投影宽度； $B_{z}$ 为中隔墙宽度； $H_{1}$ , $H_{2}$ 分别为先行洞和后行洞隧道基础至破裂面起始点的高度； $i$ =1,2,3, $\dots$ , $n$ , $n$ 为简化后导洞个数。其它符号及意义同前。

3.3 深埋非对称连拱隧道过程荷载计算公式推导

（1）先行洞和后行洞中各导洞开挖产生垂直均布荷载 $q_{11}^{i}$ , $q_{12}^{i}$

$q_{11}^{i} = γ η_{1}^{i} H_{q_{11}}^{i}$ ,

(12)

$q_{12}^{i} = γ η_{2}^{i} H_{q_{12}}^{i}$ 。

(13)

式中, $η_{1}^{i}$ , $η_{2}^{i}$ 分别为先行洞和后行洞中各导洞开挖的影响系数。

（2）拱部基本松散荷载 $q_{1}$

考虑后行洞开挖对先行洞松散荷载的加剧影响,将深埋连拱隧道先行洞和后行洞基本松散压力均简化为均布荷载 $η q_{11}$ , $q_{12}$ ：

$η q_{11} = η \sum_{i = 1}^{n} α_{1}^{i} \cdot q_{11}^{i} = η \frac{\sum_{i = 1}^{n} q_{11}^{i}^{2} b_{t_{1}}^{i}}{\sum_{i = 1}^{n} q_{11}^{i} \cdot b_{t_{1}}^{i}}$ ,

(14)

$q_{12} = \sum_{i = 1}^{n} α_{2}^{i} \cdot q_{12}^{i} = \frac{\sum_{i = 1}^{n} q_{12}^{i}^{2} b_{t_{2}}^{i}}{\sum_{i = 1}^{n} q_{12}^{i} \cdot b_{t_{2}}^{i}}$ ,

(15)

式中, $α_{1}^{i}$ , $α_{2}^{i}$ 分别为先行洞和后行洞中每个导洞引起的垂直均布荷载占先行洞和后行洞整体总荷载的大小, $η$ 为后行洞开挖对先行洞松散荷载的影响系数。

（3）中隔墙顶附加均布荷载 $q_{z}$

中隔墙顶附加的均布压力 $q_{z}$ 由极限承载拱内的附加荷载总重量 $G_{1}$ 和中隔墙顶岩土体的承载能力 $p_{s}$ 中最小值决定,即 $q_{z} = \min (G_{1} / B_{z}, p_{s})$ 。附加荷载及中隔墙顶岩土体的抗压能力可分别按下式计算：

$G_{1} = \frac{2}{3} γ B_{m} H_{m} - \frac{2}{3} γ \sum_{i = 1}^{n} B_{q_{1}}^{i} H_{q_{11}}^{i} - \frac{2}{3} γ \sum_{i = 1}^{n} B_{q_{2}}^{i} H_{q_{12}}^{i}$ ,

(16)

$p_{s} = R_{s}^{B} / K_{z}$ 。

(17)

式中 $B_{q 1}^{i} = b_{t_{1}}^{i} + (H_{t_{1}}^{i} - H_{1}) \tan (45^{\circ} - \frac{φ_{c}}{2}) + \frac{1}{2} B_{z} \cdot \frac{b_{t_{1}}^{i}}{B_{t_{1}}}$ , $B_{q 2}^{i} = b_{t_{2}}^{i} + (H_{t_{2}}^{i} - H_{2}) \tan (45^{\circ} - \frac{φ_{c}}{2}) + \frac{1}{2} B_{z} \cdot \frac{b_{t_{2}}^{i}}{B_{t_{2}}}$ ； $R_{s}^{B}$ 为中隔墙顶岩体的设计抗压强度； $K_{z}$ 为中隔墙对上部岩体支撑能力的安全系数,取值通常为2。

（4）拱部附加松散荷载 $q_{2}$ 假设 $q_{2}$ 在拱顶平面上呈三角形分布,且向上的支撑压力与承载拱内的岩土体重量平衡,由此可知

$\frac{2}{3} γ (\sum_{i = 1}^{n} B_{q_{1}}^{i} H_{q_{11}}^{i} + \sum_{i = 1}^{n} B_{q_{2}}^{i} H_{q_{12}}^{i}) + \frac{B_{m} {q^{'}}_{2}}{2} + q_{z} B_{z} = \frac{2}{3} γ B_{m} H_{m},$

(18)

$\frac{q_{21}}{{q^{'}}_{2}} = \frac{2 B_{p_{1}}}{B_{m}}$ ,

(19)

$\frac{q_{22}}{{q^{'}}_{2}} = \frac{2 B_{p_{2}}}{B_{m}}$ 。

(20)

由上式可以得到 ${q^{'}}_{2}$ , $q_{21}$ 和 $q_{22}$ 的计算式为

${q^{'}}_{2} = 2 (G_{1} - q_{z} B_{z}) / B_{m}$ ,

(21)

$q_{21} = \frac{2 B_{p_{1}}}{B_{m}} {q^{'}}_{2}$ ,

(22)

$q_{22} = \frac{2 B_{p_{2}}}{B_{m}} {q^{'}}_{2}$ 。

(23)

（5）中隔墙顶松散围岩压力荷载 $q_{3}$ 将 $q_{3}$ 可简化为三角形荷载：

$q_{3} = γ H_{q_{3}}$ ,

(24)

式中, $H_{q_{3}}$ 可以近似取为中隔墙顶到先行洞和后行洞隧道拱顶距离的平均值。

（6）侧向压力荷载

a）作用在先行洞和后行洞衬砌外侧拱部及边墙的水平方向压力荷载分别为 $e_{w 1}^{j}$ , $e_{w 2}^{j}$ ,

$e_{w 1}^{j} = λ (η q_{11} + q_{21} + γ h_{1}^{j})$ ,

(25)

$e_{w 2}^{j} = λ (q_{12} + q_{22} + γ h_{2}^{j})$ 。

(26)

式中, $h_{1}^{j}$ , $h_{2}^{j}$ 分别为先行洞和后行洞拱顶外侧到计算点的距离, $λ$ 为侧压力系数,按朗金公式计算, $λ = \tan^{2} (45^{\circ} - φ_{c} / 2)$ 。

b）作用在先行洞和后行洞衬砌内侧拱部及边墙的水平方向压力荷载分别为 $e_{n 1}^{j}$ , $e_{n 2}^{j}$ ,

$e_{n 1}^{j} = λ (η q_{11} + {q^{'}}_{2} + q_{3}^{j})$ ,

(27)

$e_{n 2}^{j} = λ (q_{12} + {q^{'}}_{2} + q_{3}^{j})$ ,

(28)

式中, $q_{3}^{j}$ 为衬砌外侧拱部及边墙计算点 $q_{3}$ 荷载的大小。

4. 公式计算分析

4.1 对比分析

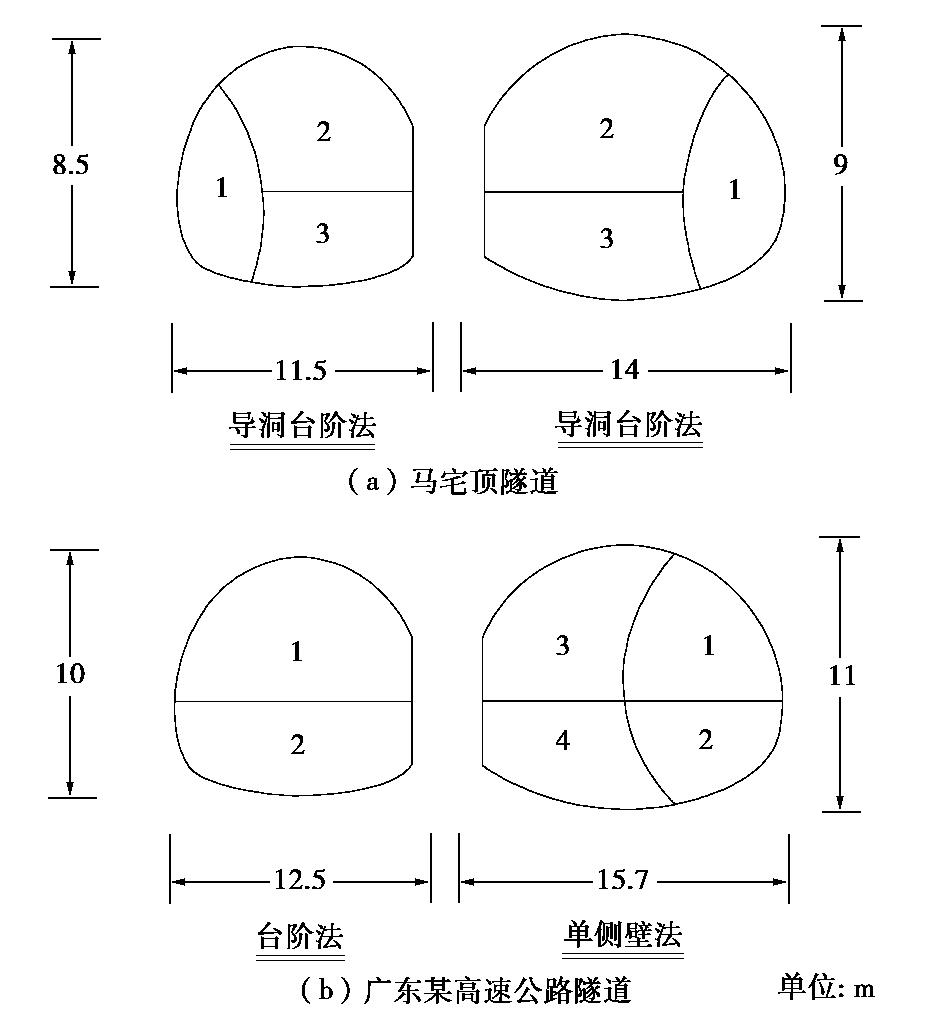
当深埋非对称连拱隧道围岩压力计算不考虑后行洞开挖对先行洞松动荷载的加剧影响以及左右洞室施工过程时,本文推导的过程荷载计算方法将退化为李鹏飞等^[16]提出的围岩压力计算方法。因此,在不考虑施工过程影响（方法1）和考虑施工过程影响（方法2）两种条件下,分别采用本文推导的公式对文献[16]中工程案例的围岩压力进行计算,对比文献中公式的计算结果,以验证本文推导的深埋非对称连拱隧道过程荷载计算方法的正确性。计算断面围岩等级为Ⅴ级,埋深50 m,中隔墙宽度3 m,左洞（先行洞）和右洞（后行洞）开挖跨度分别为11.5,14 m,开挖高度分别为8.5,9 m,计算摩擦角取45°,重度取20 kN/m³。计算结果如表3所示。

表 3 深埋非对称连拱隧道围岩压力计算

Table 3. Calculation of rock pressures of deep-buried asymmetric multi-arch tunnels

方法	$q_{11}$ ( $η q_{11}$ )/kPa	$q_{12}$ /kPa	$q_{21}$ /kPa	$q_{22}$ /kPa	${q^{'}}_{2}$ /kPa	$q_{3}$ /kPa	$q_{z}$ /kPa
文献[16]	197	227	35	34	217	59	400
本文方法1	197	227	35	34	217	59	400
本文方法2	119(156)	146	96.	106	305	59	400

下载: 导出CSV

| 显示表格

根据计算结果可以看出,在忽略施工过程影响的条件下,采用本文推导的公式计算非对称连拱隧道各部分荷载与李鹏飞等^[16]提出公式的计算结果基本一致,验证了深埋非对称连拱隧道过程荷载计算方法的正确性。同时,计算结果显示,在考虑施工过程影响的条件下,本文方法计算的双洞拱部基本围岩压力较小,而拱部附加围岩压力较大,这比较符合非对称双连拱隧道真实的受力情况。由于在施工过程中围岩受到多次扰动,拱部围岩受力状态不如单洞情况,特别是围岩较差的情况下,后行洞施工往往会对拱部附加围岩压力产生更显著的影响,因此,本文提出的深埋非对称连拱隧道过程荷载计算方法考虑的影响因素更为全面,更符合工程实际。

4.2 工程实例计算与分析

深埋非对称连拱隧道在国内外比较罕见,本文依托罗长高速公路马宅顶隧道^[20]和广东省某高速公路隧道连拱段两项工程,利用推导的过程荷载计算方法对其围岩压力进行计算,并对比现场监测数据,分析公式的实用性。各取两项工程中一深埋围岩压力监测断面,计算参数如表4所示,开挖方法及开挖顺序示意图如图6所示。

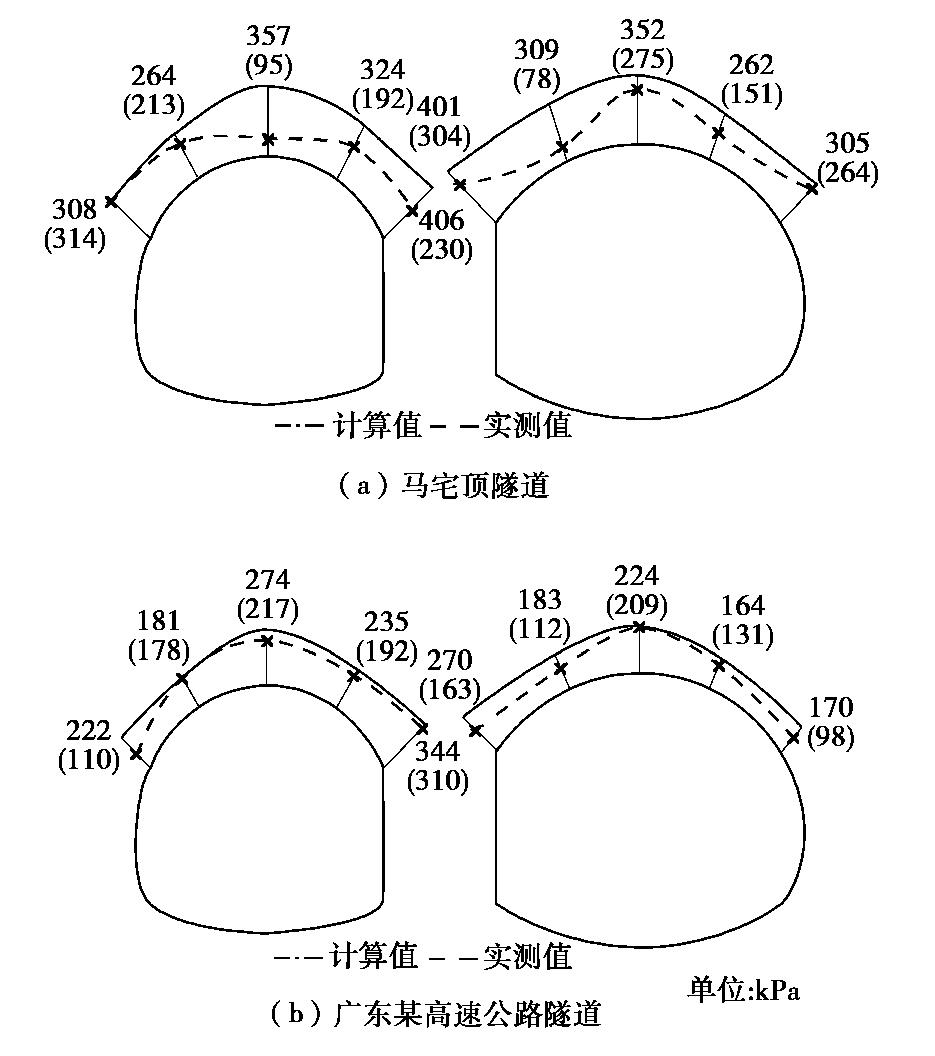
表 4 马宅顶隧道和广东某公路隧道监测断面计算参数

Table 4. Parameters of monitoring section of Mazhaiding Tunnel and a highway tunnel in Guangdong

项目	围岩等级	埋深/m	重度/(kN·m^-3)	高度和跨度/m		中隔墙宽度/m	计算摩擦角/（°）
项目	围岩等级	埋深/m	重度/(kN·m^-3)	先行洞	后行洞	中隔墙宽度/m	计算摩擦角/（°）
马宅顶隧道	Ⅴ	50	20	8.5/11.5	9/14	3	45
广东某公路隧道	Ⅳ	70	22	10/12.5	11/15.7	3.5	55

下载: 导出CSV

| 显示表格

图 6 开挖方法及开挖顺序示意图

Figure 6. Sketch maps of excavation method and sequence

下载: 全尺寸图片幻灯片

根据计算参数,按照深埋非对称连拱隧道过程荷载计算公式对监测断面进行计算,将各部分荷载沿隧道开挖轮廓线叠加,绘制非对称连拱隧道计算围岩压力分布图,并与现场监测数据进行对比,如图7所示。由图可知,除马宅顶先行洞左拱腰实测值大于计算值外,其余各监测点现场实测值均略小于计算值,即计算值对实测值起到了很好的包络效果,且广东某高速公路隧道连拱段的包络效果优于马宅顶隧道,这是由于围岩质量越低,开挖工序更加复杂,后行洞开挖对先行洞产生的二次扰动越明显,现场监测数据更易受到影响。同时,两组计算值均表现出中隔墙两侧拱腰处围岩压力值大于拱肩处,这与实测结果的规律基本一致。以上两点从侧面证明了本文推导的非对称连拱隧道过程荷载计算方法具有一定的合理性和实用性。需要指出的是,由于现场诸多因素会影响到监测数据的采集,并且围岩压力的监测滞后于开挖,只能在初支架设之后进行,因此监测结果多为相对于量测开始时的应力变化,仅在一定程度上能够反映实际的围岩压力情况。

图 7 围岩压力计算值与实测值的对比图

Figure 7. Comparison between calculated and measured values

下载: 全尺寸图片幻灯片

5. 结论

（1）与不考虑施工过程的围岩压力计算公式相比,本文推导的过程荷载计算方法得到的双洞拱部基本围岩压力较小,而拱部附加围岩压力较大,且围岩质量越差,这种差别越明显。

（2）中隔墙两侧拱腰处计算围岩压力值大于相邻拱肩处,且围岩质量越低,后行洞开挖对先行洞产生的二次扰动越明显,先行洞内外侧、后行洞内侧围岩压力值均不断增大。

（3）本文推导计算方法得到的围岩压力分布规律与现场监测获取的围岩压力分布规律基本一致,论证了本文推导公式的合理性,对深埋非对称连拱隧道合理施工方案的确定以及支护结构的设计和优化具有一定的指导意义和参考价值。

图 1 微流控芯片制备示意图

Figure 1. Schematic images of fabrication process of microchip

下载: 全尺寸图片幻灯片

图 2 微流控系统示意图

Figure 2. Schematic images of microfluidics system

下载: 全尺寸图片幻灯片

图 3 显微拍摄示意图及图像

Figure 3. Schematic diagram of microscopy and digital photographs

下载: 全尺寸图片幻灯片

图 4 微生物矿化胶结砂颗粒时序图

Figure 4. Sequence photographs of cementation of sand particles over course of MICP experiment

下载: 全尺寸图片幻灯片

图 5 微管道中碳酸钙晶体随时间分布图

Figure 5. Spatial distribution of bulk crystals during different reaction periods in microchannel

下载: 全尺寸图片幻灯片

图 6 管道横截面不同位置处晶体分布图

Figure 6. Spatial distribution of bulk crystals at microchannel cross-section

下载: 全尺寸图片幻灯片

图 7 不同沉积模式下碳酸钙晶体的生长速率

Figure 7. Crystal growth rate of different precipitation patterns

下载: 全尺寸图片幻灯片

参考文献(25)

[1]	何稼, 楚剑, 刘汉龙, 等. 微生物岩土技术的研究进展[J]. 岩土工程学报, 2016, 38(4): 643-653. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201604010.htm HE Jia, CHU Jian, LIU Han-long, et al. Research advances in biogeotechnologies[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 643-653. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201604010.htm
[2]	刘汉龙, 肖鹏, 肖杨, 等. 微生物岩土技术及其应用研究新进展[J]. 土木与环境工程学报(中英文), 2019, 41(1): 1-14. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201901001.htm LIU Han-long, XIAO Peng, XIAO Yang, et al. State-of-the-art review of biogeotechnology and its engineering applications[J]. Journal of Civil and Environme- ntal Engineering, 2019, 41(1): 1-14. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201901001.htm
[3]	WHIFFIN V S, VAN PAASSEN L A, HARKES M P. Microbial carbonate precipitation as a soil improvement technique[J]. Geomicrobiology Journal, 2007, 24(5): 417-423. doi: 10.1080/01490450701436505
[4]	DEJONG J T, SOGA K, KAVAZANJIAN E, et al. Biogeochemical processes and geotechnical applications: Progress, opportunities and challenges[J]. Geotechnique, 2013, 63(4): 287-301. doi: 10.1680/geot.SIP13.P.017
[5]	VAN PAASSEN L A, GHOSE R, VAN DER LINDEN T J M, et al. Quantifying biomediated ground improvement by ureolysis: large-scale biogrout experiment[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(12): 1721-1728. doi: 10.1061/(ASCE)GT.1943-5606.0000382
[6]	CUI M J, ZHENG J J, ZHANG R J, et al. Influence of cementation level on the strength behaviour of bio-cemented sand[J]. Acta Geotechnica, 2017, 12(5): 971-986. doi: 10.1007/s11440-017-0574-9
[7]	XIAO Y, WANG Y, DESAI C S, et al. Strength and deformation responses of biocemented sands using a temperature-controlled method[J]. International Journal of Geomechanics, 2019, 19(11): 04019120. doi: 10.1061/(ASCE)GM.1943-5622.0001497
[8]	崔明娟, 郑俊杰, 章荣军, 等. 化学处理方式对微生物固化砂土强度影响研究[J]. 岩土力学, 2015, 36(增刊1): 392-396. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S1068.htm CUI Ming-juan, ZHENG Jun-jie, ZHANG Rong-jun, et al. Study of effect of chemical treatment on strength of bio-cemented sand[J]. Rock and Soil Mechanics, 2015, 36(S1): 392-396. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S1068.htm
[9]	XIAO P, LIU H, STUEDLEIN A W, et al. Effect of relative density and biocementation on cyclic response of calcareous sand[J]. Canadian Geotechnical Journal, 2019, 56(12): 971-986.
[10]	XIAO Y, HE X, EVANS T M, et al. Unconfined compressive and splitting tensile strength of basalt fiber-reinforced biocemented sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(9): 04019048. doi: 10.1061/(ASCE)GT.1943-5606.0002108
[11]	彭劼, 温智力, 刘志明, 等. 微生物诱导碳酸钙沉积加固有机质黏土的试验研究[J]. 岩土工程学报, 2019, 41(4): 733-740. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904022.htm PENG Jie, WEN Zhi-li, LIU Zhi-ming, et al. Experimental research on MICP-treated organic clay[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 733-740. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904022.htm
[12]	XIAO Y, STUEDLEIN A W, RAN J Y, et al. Effect of particle shape on strength and stiffness of biocemented glass beads[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(11): 06019016. doi: 10.1061/(ASCE)GT.1943-5606.0002165
[13]	CHENG L, CORD-RUWISCH R, SHAHIN M A. Influence of key environmental conditions on microbially induced cementation for soil stabilization[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(1): 04016083. doi: 10.1061/(ASCE)GT.1943-5606.0001586
[14]	DEJONG J T, FRITZGES M, B, NüSSLEIN K. Microbially induced cementation to control sand response to undrained shear[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(11): 1381-1392.
[15]	TAGLIAFERRI F, WALLER J, ANDÒ E, et al. Observing strain localisation processes in bio-cemented sand using X-ray imaging[J]. Granular Matter, 2011, 13(3): 247-250.
[16]	DEJONG J T, MORTENSEN B M, MARTINEZ B C, et al. Bio-mediated soil improvement[J]. Ecological Engineering, 2010, 36(2): 197-210.
[17]	ZHANG W, JU Y, ZONG Y, et al. In situ real-time study on dynamics of microbially induced calcium carbonate precipitation at a single-cell level[J]. Environmental Science & Technology, 2018, 52(16): 9266-9276.
[18]	WHITESIDES G M. The origins and the future of microfluidics[J]. Nature, 2006, 442(7101): 368-373.
[19]	WANG Y, SOGA K, DEJONG J T, et al. A microfluidic chip and its use in characterising the particle-scale behaviour of microbial-induced calcium carbonate precipitation (MICP)[J]. Géotechnique, 2019, 69(12): 1086-1094.
[20]	ROSSY T, NADELL C D, PERSAT A. Cellular advective-diffusion drives the emergence of bacterial surface colonization patterns and heterogeneity[J]. Nature Communications, 2019, 10(1): 2471-2480.
[21]	CHILTON T H, COLBURN A P. Pressure drop in packed tubes[J]. Industrial and Engineering Chemistry, 1931, 23(8): 913-919.
[22]	HAYNES W M. CRC Handbook of Chemistry and Physics[M]. Boca Raton: CRC Press, 2014.
[23]	GOSTING L J, AKELEY D F. A study of the diffusion of urea in water at 25-degrees with the Gouy interference method[J]. Journal of the American Chemical Society, 1952, 74(8): 2058-2060.
[24]	ZENG Y, CAO J, WANG Z, et al. Formation of amorphous calcium carbonate and its transformation mechanism to crystalline CaCO₃ in laminar microfluidics[J]. Crystal Growth & Design, 2018, 18(3): 1710-1721.
[25]	MCDONALD J C, DUFFY D C, ANDERSON J R, et al. Fabrication of microfluidic systems in poly (dimethylsiloxane)[J]. Electrophoresis, 2000, 21(1): 27-40.

施引文献(28)

期刊类型引用(12)

1.	席玉宇，冯珂，高景明. 超大断面分岔隧道软弱围岩过渡段施工力学特性研究. 价值工程. 2025(08): 56-59 . 百度学术
2.	王恒. 浅埋偏压隧道管棚注浆加固效应分析. 北方交通. 2024(08): 83-87 . 百度学术
3.	侯艳娟，张顶立，李然，陈旭，齐伟伟. 深埋三连拱隧道围岩压力计算方法. 力学学报. 2024(11): 3213-3226 . 百度学术
4.	何丹，郭亚林，林宇亮，肖洪波，张沛然. 地形偏压对连拱隧道支护结构及围岩的影响. 公路交通科技. 2024(11): 167-177 . 百度学术
5.	李志厚，王安民，陈树汪，陈俊武，邓志云. 无中导连拱隧道受力机理及对策研究. 地下空间与工程学报. 2024(06): 1969-1978 . 百度学术
6.	姜成业，汤华，邓琴，和振海，毕钛俊. 深埋无中导洞连拱隧道围岩压力计算方法研究. 中南大学学报(自然科学版). 2023(03): 1168-1177 . 百度学术
7.	刘建生. 大跨度偏压连拱隧道洞口段施工力学性能研究. 公路. 2023(04): 423-428 . 百度学术
8.	白宏达，王安民，王少飞，张伟，喻佳. 台阶-CRD无中导洞连拱隧道施工响应分析. 公路交通科技. 2023(03): 173-181 . 百度学术
9.	刘昶，刘辉，邓小钊，张艺，张妞. 偏压连拱隧道非对称中隔墙施工力学特性研究. 交通科学与工程. 2021(03): 50-57+77 . 百度学术
10.	李占华. 大跨度隧道施工单体洞室开挖方法研究. 工程机械与维修. 2021(05): 182-185 . 百度学术
11.	余俊，翁贤杰，樊文胜，张连震. 松散地层隧道进洞段管棚注浆加固效应分析. 山东大学学报(工学版). 2020(06): 92-100 . 百度学术
12.	胡新朋，王登锋，肖本利. 分岔隧道安全高效施工方法优化研究. 隧道建设(中英文). 2020(S2): 210-215 . 百度学术