土体等向固结曲线的Logistic模型

周凤玺; 邵彦平; MUSAAbdallah Ibrahim Ahmed

doi:10.11779/CJGE202005021

土体等向固结曲线的Logistic模型 English Version

1.
兰州理工大学土木工程学院,甘肃　兰州　730050
2.
西部土木工程防灾减灾教育部工程研究中心,甘肃　兰州　730050

基金项目:

国家自然科学基金项目 11962016

国家自然科学基金项目 51978320

甘肃省陇原青年创新创业人才资助项目 059003

详细信息

作者简介:
周凤玺(1979—),男,博士,主要从事岩土工程方面的教学与研究工作。E-mail: geolut@163.com

中图分类号: TU43
计量
- 文章访问数: 318
- HTML全文浏览量: 24
- PDF下载量: 148
出版历程
- 收稿日期: 2019-06-11
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-04-30

Logistic model for isotropic consolidation curve of soils

1.
School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China
2.
Western Engineering Research Center of Disaster Mitigation in Civil Engineering of Ministry of Education, Lanzhou University of Technology, Lanzhou 730050, China

摘要

摘要: 基于非饱和土等向压缩试验和Logistic函数,提出了一种土体等向固结曲线的模型。首先,对目前土体体变方程中常用的单对数和双对数线性模型的不足进行了分析；然后,借助Logistic函数,建立了各向等压条件下的土体孔隙比和压力模型,并给出了模型中各参数的确定方法以及前期固结压力的解析表达；最后,通过与已有试验数据进行对比,验证了该模型的有效性,分析了各参数随非饱和土中吸力的变化规律。
- 等向压缩曲线 /
- 非饱和土 /
- Logistic函数 /
- 前期固结压力
Abstract: Based on the isotropic compression tests on unsaturated soils and the Logistic function, a model for isotropic consolidation curve of soils is proposed. Firstly, the shortcomings of the single-logarithmic and double-logarithmic linear models commonly used in the volumetric behavior are analyzed. Then, with the Logistic function, the mathematical model between void ratio and pressure under isotropic compression conditions is established. The determination method for every parameter in the model and the analytical expression of the pre-consolidation pressure are given. Finally, the validity of the model is verified by comparison with the existing experimental data, and the influence of suction on each model parameter is analyzed.
- isotropic compression curve /
- unsaturated soil /
- Logistic function /
- pre-consolidation pressure

HTML全文

0. 引言

标志着现代土力学理论开端的剑桥模型将固结和剪切有效的统一起来,成为广泛应用的土的弹塑性模型。然而剑桥模型基于饱和土建立,如何将其推广到非饱和土的弹塑性模型中去,已成为土力学理论的研究热点之一^[1-9]。在非饱和土本构模型研究的发展过程中等向固结曲线,即孔隙比e或比体积( $v = 1 + e$ )与平均有效应力 $p^{'}$ 或平均净应力 $\bar{p}$ 的关系在建立非饱和土本构模型中有着非常重要的作用。其中,净应力 $\bar{p} = p - u_{a}$ ,平均有效应力 $p^{'} = \bar{p} - S_{r} s$ ,基质吸力 $s = u_{a} - u_{w}$ , $u_{a}$ , $u_{w}$ 分别为孔隙气压力和孔隙水压力。

大量的试验表明,即使是没有经过超固结的非饱和土,在常吸力条件下的正常固结线在孔隙比和对数平均压力空间上为一条曲线^[4-5]。目前描述土体等向压缩线的方法中常用的有单对数线性模型^[6-10]和双对数线性模型^[4-5,9]。

Roscoe等^[10]在饱和正常固结土和弱超固结土的试验基础上,提出了各向等压固结中孔隙比或比体积将会沿正常固结线（NCL）变化,并且近似满足：

$e = N - λ \ln p^{'}$ ,

(1)

式中,e, $p^{'}$ 分别为饱和土的孔隙比和平均有效应力, $N$ 为NCL在 $p^{'} = 1 kPa$ 时对应的孔隙比, $λ$ 为NCL在 $e - \ln p^{'}$ 平面的斜率。

卸载和回弹过程的孔隙比变化和平均有效应力的关系表示为

$e = Γ - κ \ln p^{'}$ ,

(2)

式中, $Γ$ 为回弹线（SL）在卸载到 $p^{'} = 1 kPa$ 时对应的孔隙比, $κ$ 为SL在 $e - \ln p^{'}$ 平面的斜率。

为了建立非饱和土的弹塑性本构模型,许多学者^[6-8]将式（1）,（2）直接进行了扩展,即各向等压曲线和回弹曲线分别为

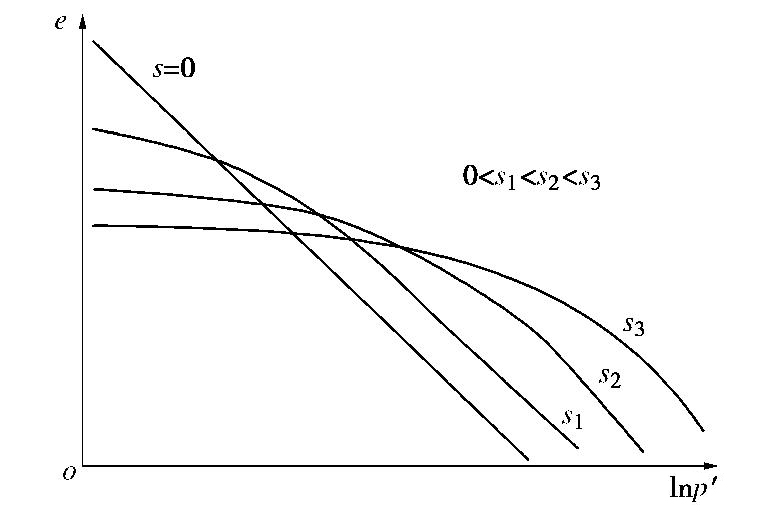
$\begin{matrix} NCL ： & e = N (s) - λ (s) \ln p^{'} \end{matrix}$ ,

(3)

$\begin{matrix} SL: & e = Γ (s) - κ (s) \ln p^{'} \end{matrix}$ ,

(4)

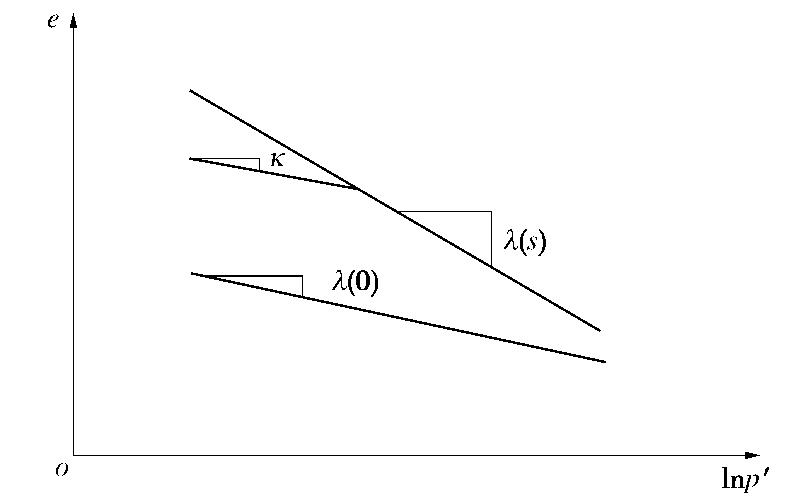
式中, $N (s)$ , $λ (s)$ , $Γ (s)$ 和 $κ (s)$ 的含义与式（1）,（2）相同,但均为基质吸力 $s = u_{a} - u_{w}$ 的函数。式（3）,（4）表示的NCL和SL在 $e - \ln p^{'}$ 平面如图1所示。

图 1 单对数线性模型^[7]

Figure 1. Single-logarithmic approach^[7]

下载: 全尺寸图片幻灯片

与式（1）,（2）类似,相同基质吸力s条件下,NCL和SL上孔隙比与平均有效应力或平均净应力的对数成线性关系,然而这种近似有诸多不合理之处^[11]。如式（3）表示在等向压缩条件下,孔隙比的变化量与前期固结压力无关,只与压力的变化范围有关；式（4）表示的回弹线SL上,当 $p^{'}$ 增加到一定值后,孔隙比 $e$ 将成为负数,并且当 $p^{'} \to 0$ 时, $e \to \infty$ ,在理论上和实际上均不合理。为了克服 $e - \ln p^{'}$ 线性近似的不足,考虑饱和土 $\ln e - \ln p^{'}$ 为双对数线性关系式：

$d (ln e) = - λ_{vp} d (\ln p^{'}) = - λ_{vp} \frac{d p}{p - u_{w}} + λ_{vp} \frac{d u_{w}}{p - u_{w}}$ ,

(5)

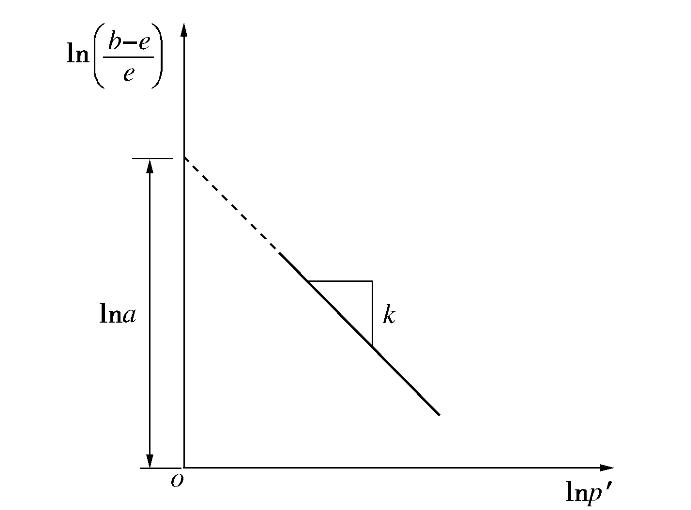
式中, $p^{'} = p - u_{w}$ 为Terzaghi有效应力, $λ_{vp}$ 为饱和土NCL的斜率。

SHENG等^[5,12]采用双应力变量将式（5）扩展到非饱和土,如图2所示给出了非饱和土的各向等压固结曲线方程：

$d(ln e) = - λ_{vp} \frac{d \bar{p}}{\bar{p} + s} - λ_{vs} (s) \frac{d s}{\bar{p} + s}$ ,

(6)

图 2 双对数线性模型^[5]

Figure 2. Double-logarithmic approach^[5]

下载: 全尺寸图片幻灯片

式中, $λ_{v p}$ 是一个材料常数,与吸力无关, $λ_{vs}$ 则是一个随吸力变化的参数,饱和时 $λ_{v p} = λ_{vs}$ 。该式把体积变化划分为两部分：①净应力的改变引起的,②吸力的改变引起的,两部分引起的变形会有所不同。类似于式（6）,SL方程可写为

$d(ln e) = - κ_{vp} \frac{d \bar{p}}{\bar{p} + s} - κ_{vs} (s) \frac{d s}{\bar{p} + s}$ ,

(7)

式中, $κ_{vs}$ 为回弹曲线的斜率,与吸力有关,土体达到饱和时 $λ_{vp} = λ_{vs}$ 。

虽然双对数模型可以解决单一对数模型中存的许多问题,但式（6）,（7）中人为的将斜率 $λ$ 或 $κ$ 分为 $λ_{vp}$ 或 $κ_{vp}$ 以及 $λ_{vs} (s)$ 或 $κ_{vs} (s)$ 两种情况,缺乏理论依据,并且由于采用了双应力变量模型,无法直接从非饱和土过度到饱和状态^[13]。

1. 各向等压固结的Logistic模型

土体的等向压缩线由于结构性和各向异性等原因基本呈现平缓变化段和陡峭段两个阶段（图3）。笔者通过对大量试验数据的整理发现在等向压缩过程中 $e - \ln p^{'}$ 曲线符合Logistic函数。需要说明的是研究已表明土体在弹性阶段,回弹曲线的斜率几乎不受吸力变化的影响,但塑性阶段的斜率明显受吸力的影响,但是在通过比较不同应力变量,净应力 $e - \ln \bar{p}$ 和平均有效应力 $e - \ln p^{'}$ 平面中的等向固结线的变化情况,两者的变化趋势相同,因此本文均采用 $e - \ln p^{'}$ 表示。

图 3 等压固结曲线示意图

Figure 3. Schematic illustration of isotropic compression line

下载: 全尺寸图片幻灯片

1.1 模型建立

Logistic函数是一种常见的S形函数,在预测种群增长方面有着广泛的应用,其微分形式如下^[14]

$\frac{d N}{d t} = k N (1 - \frac{N}{b})$ 。

(8)

式中 N,t分别为所研究种群的数量和时间； $k$ , $b$ 为待定的模型参数。考虑到Logistic函数可以有效地描述种群数量的增长起初阶段为指数增长,然后随着变得饱和,增加变慢,最后达到成熟时增加停止的规律,这与土体的正常固结曲线相一致。因此,在半对数坐标系 $e - \ln p^{'}$ 中引入Logistic函数来描述土体的正常固结特性,根据式（8）其微分形式可重写为

$\frac{d(\ln e)}{d(\ln p^{'})} = k (1 - \frac{e}{b})$ 。

(9)

可看出,当式（8）,（9）中的 $1 / b = 0$ ,即为双对数线性模型。虽然双对数线性模型中考虑了孔隙变化与当前孔隙比的关系,但认为孔隙比的变化量仅仅与压力的对数变化范围有关,而未考虑当前压力的大小。

对式（9）进行积分并整理可得

$e = \frac{b}{1 + a \exp [- k \ln (p^{'})]} = \frac{b}{1 + a {p^{'}}^{- k}}$ ,

(10)

式中, $a$ 为积分常数。

对于卸载回弹线SL,仍采用半对数线性模型,但与SHEN^[7]不同,不再人为的将SL斜率分为 $κ_{vp}$ 和 $κ_{vs} (s)$ 两种状态。实际上由于吸力对SL斜率影响很小,因此考虑如下关系：

$\frac{d e}{d(\ln p^{'})} = κ$ ,

(11)

式中, $κ$ 为卸载回弹线在 $e - \ln p^{'}$ 平面的斜率。

式（10）,（11）给出了含有3参数的等压固结线Logistic模型及含有1参数的卸载回弹半对数线性模型。

1.2 模型参数确定

通过对式（10）进行分析可以得到,当等向压力 $p^{'} = 0$ 时,参数 $b = e_{0}$ 即为土体的初始孔隙比。当等向压力 $p^{'} = 1 kPa$ 时,参数 $a = \frac{b - e_{1}}{e_{1}} = \frac{e_{0}}{e_{1}} - 1$ ,其中 $e_{1}$ 为土体在 $p^{'} = 1 kPa$ 时的孔隙比。由于在压力较小时孔隙比不容易准确测定,因此也可用拟合的方法确定。

根据式（10）整理可得

$\ln (\frac{b - e}{e}) = \ln a - k \ln p^{'}$ 。

(12)

式（12）表明,在 $\ln (\frac{b - e}{e})$ 和 $\ln p^{'}$ 平面内为线性关系,且直线的斜率和截距分别为 $k$ 和 $\ln a$ ,如图4所示,这样就可以很方便地确定模型中的参数 $k$ 和 $a$ 了。式（11）中SL斜率 $κ$ 亦可采用类似的方法获得。

图 4 确定参数a和k示意图

Figure 4. Schematic view for determining a and k

下载: 全尺寸图片幻灯片

1.3 先期固结压力

为了获得非饱和土各向等压固结线上的前期固结压力 ${p^{'}}_{c}$ ,采用与传统相类似的三步骤方法^[15],通过几何关系确定出坐标点B,C（图3）。

式（10）的一阶导数和二阶导数分别为

$\frac{d e}{d (\ln p^{'})} = \frac{k a b \exp (- k \ln p^{'})}{{[1 + a \exp (- k \ln p^{'})]}^{2}}$ ,

(13)

$\frac{d^{2} e}{d(\ln p^{'})^{2}} = \frac{k^{2} a b \exp (- k \ln p^{'}) [a \exp (- k \ln p^{'}) - 1]}{{[1 + a \exp (- k \ln p^{'})]}^{3}}$ 。

(14)

由式（14）可得到曲线的反弯点B点坐标为 $(\ln a / k, b / 2)$ ,将其代入式（13）中可得到曲线在B点处的斜率为 $k b / 4$ 。

则过B点的切线BC可表示为

$e = \frac{k b}{4} (\ln p^{'} - \frac{\ln a}{k}) + \frac{b}{2}$ 。

(15)

考虑 $e = e_{0} = b$ ,且与切线方程式（15）相交,即可得到交点C处的前期固结压力为

$\ln {p^{'}}_{c} = \frac{4 + \ln a}{k} - \frac{b}{2}$ 。

(16)

2. 分析与讨论

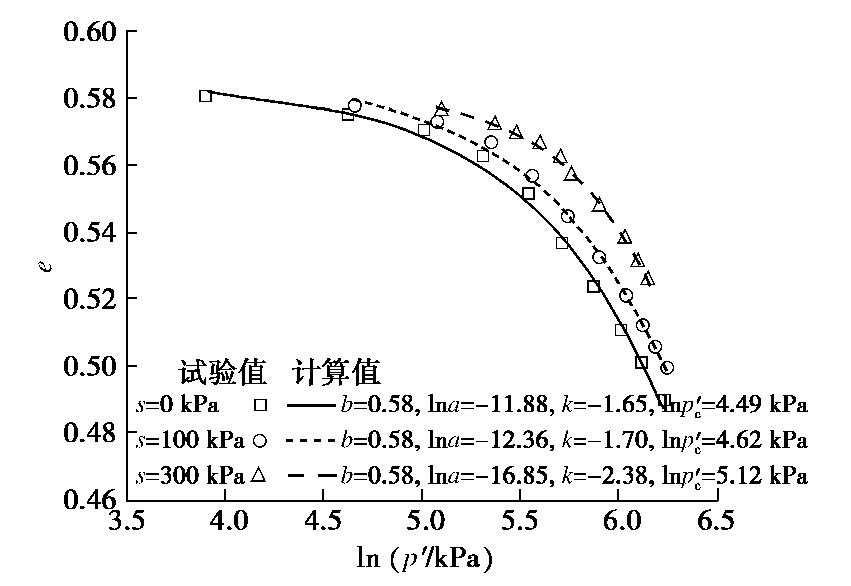
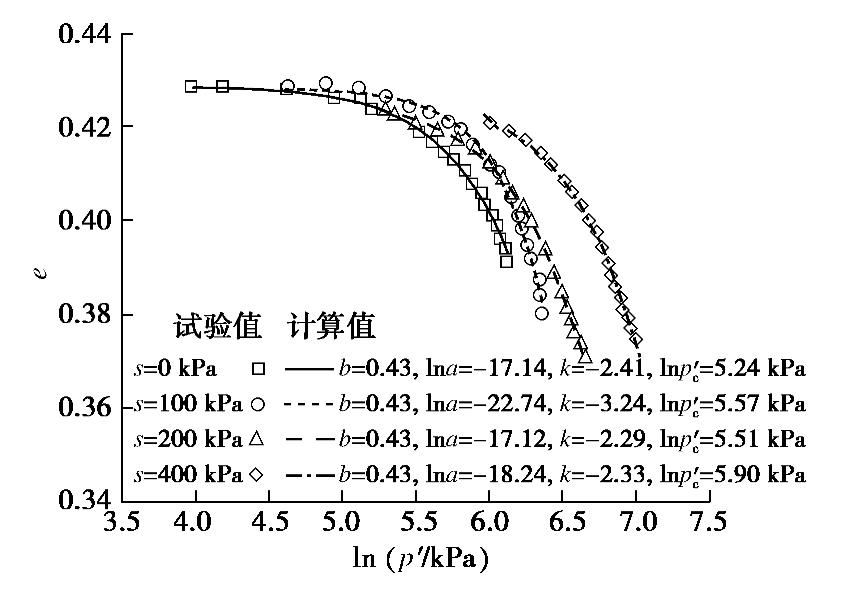
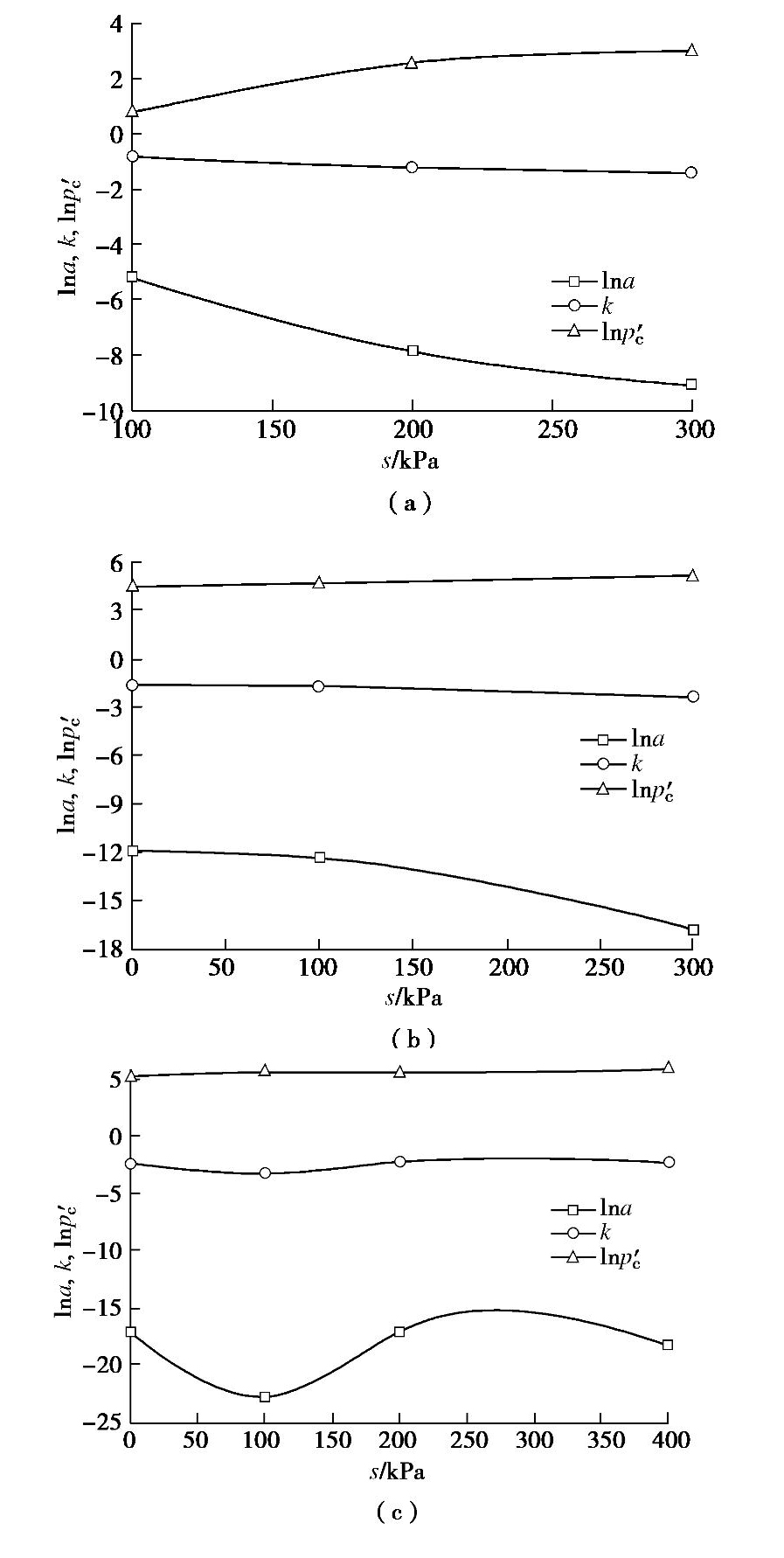
为了验证本文提出的非饱和土等向固结曲线模型,与Sharma等^[16]、Bellia等^[17]、Burland等^[18]的试验结果进行比对分析。图5～7为在不同基质吸力s条件下的试验数据和本文模型预测值的对比,图中并给出了相应的模型参数。从图可看出,Logstic函数可以很好地描述土体在等向压缩固结条件下的孔隙比变化趋势。对于非饱和土,模型（10）中的参数a,k以及前期固结压力 ${p^{'}}_{c}$ 和土中基质吸力s相关。图8（a）～8（c）依次给出了与Sharma^[16]、Bellia^[17]和Burland等^[18]的试验数据相应的模型参数lna,k和 ${p^{'}}_{c}$ 随吸力的变化曲线。从图中可以看出,随着基质吸力s的变化,参数lna和k并没有一个统一的规律,这与其它模型的固结曲线斜率随吸力的变化结论相一致,而前期固结压力 ${p^{'}}_{c}$ 随着吸力的增大呈增加趋势。

图 5 与Sharma等^[16]的试验对比

Figure 5. Comparison between proposed model and experimental data of Sharma et al^[16]

下载: 全尺寸图片幻灯片

图 6 与Bellia等^[17]的试验对比

Figure 6. Comparison between proposed model and experimental data of Bellia et al^[17]

下载: 全尺寸图片幻灯片

图 7 与Burland等^[18]的试验对比

Figure 7. Comparison between proposed model and experimental data of Burland et al^[18]

下载: 全尺寸图片幻灯片

图 8 参数a, k以及前期固结压力

${p^{'}}_{c}$ 随吸力s的变化曲线

Figure 8. Variations of parameters a, k and pre-consolidation pressure

${p^{'}}_{c}$ with suction s

下载: 全尺寸图片幻灯片

采用Burland等^[18]的在基质吸力分别为0,400 kPa时的试验数据,图9,10分别对本文提出的Logistic模型和 $e - \ln p^{'}$ 半对数模型以及 $\ln e - \ln p^{'}$ 双对数模型进行了比对。从图中可以看出Logistic模型较之可以更好地描述土体的等向固结行为。

图 9 与半对数线性模型比较

Figure 9. Comparison between proposed model and semi-logarithmic linear model

下载: 全尺寸图片幻灯片

图 10 与双对数线性模型比较

Figure 10. Comparison between proposed model and double-logarithmic model

下载: 全尺寸图片幻灯片

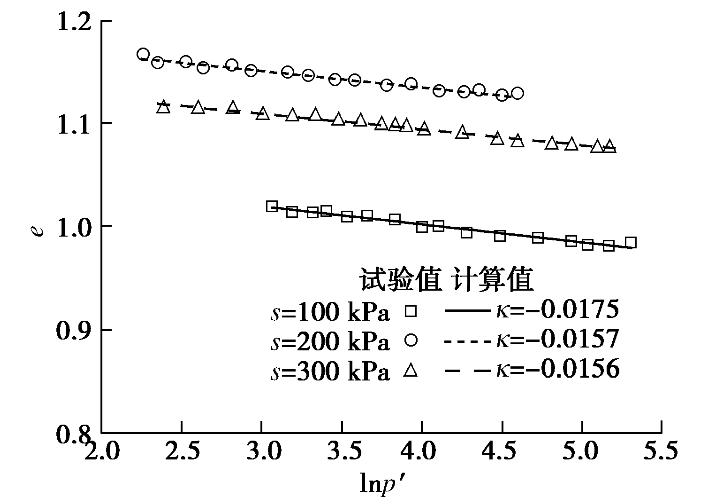
对于卸载回弹曲线SL,采用 $e - \ln p^{'}$ 半对数线性模型,即式（11）可以进行很好的描述。图11给出了Sharma等^[16]的回弹数据与预测值的对比,可以看出非饱和土中吸力对回弹曲线的斜率影响不大。

图 11 卸载回弹曲线对比

Figure 11. Comparison between experimental data of Sharma et al^[16] and Eq.(11)

下载: 全尺寸图片幻灯片

3. 结论

考虑到土体的体积变形量不仅与荷载的变化范围有关,还与当前的荷载大小以及孔隙比大小有关,通过引入Logistic函数,建立了土体在等向压缩条件下的Logistic曲线模型,对于卸载回弹曲线,采用了半对数线性模型。通过与已有试验数据的分析和对比,发现本文提出的等向压缩曲线模型和回弹曲线模型可以很好的描述非饱和土的体变特性,并且模型中的各参数方便获取。

图 1 单对数线性模型^[7]

Figure 1. Single-logarithmic approach^[7]

下载: 全尺寸图片幻灯片

图 2 双对数线性模型^[5]

Figure 2. Double-logarithmic approach^[5]

下载: 全尺寸图片幻灯片

图 3 等压固结曲线示意图

Figure 3. Schematic illustration of isotropic compression line

下载: 全尺寸图片幻灯片

图 4 确定参数a和k示意图

Figure 4. Schematic view for determining a and k

下载: 全尺寸图片幻灯片

图 5 与Sharma等^[16]的试验对比

Figure 5. Comparison between proposed model and experimental data of Sharma et al^[16]

下载: 全尺寸图片幻灯片

图 6 与Bellia等^[17]的试验对比

Figure 6. Comparison between proposed model and experimental data of Bellia et al^[17]

下载: 全尺寸图片幻灯片

图 7 与Burland等^[18]的试验对比

Figure 7. Comparison between proposed model and experimental data of Burland et al^[18]

下载: 全尺寸图片幻灯片

图 8 参数a, k以及前期固结压力 ${p^{'}}_{c}$ ${p^{'}}_{c}$ 随吸力s的变化曲线

Figure 8. Variations of parameters a, k and pre-consolidation pressure ${p^{'}}_{c}$ ${p^{'}}_{c}$ with suction s

下载: 全尺寸图片幻灯片

图 9 与半对数线性模型比较

Figure 9. Comparison between proposed model and semi-logarithmic linear model

下载: 全尺寸图片幻灯片

图 10 与双对数线性模型比较

Figure 10. Comparison between proposed model and double-logarithmic model

下载: 全尺寸图片幻灯片

图 11 卸载回弹曲线对比

Figure 11. Comparison between experimental data of Sharma et al^[16] and Eq.(11)

下载: 全尺寸图片幻灯片

参考文献(18)

[1]	ALONSO E E, GENS A, JOSA A. A constitutive model for partially saturated soils[J]. Géotechnique, 1990, 40(3): 405-430. doi: 10.1680/geot.1990.40.3.405
[2]	XIONG Y L, YANG Q L, ZHANG S, et al. Thermo- elastoplastic model for soft rock considering effects of structure and overconsolidation[J]. Rock Mechanics and Rock Engineering, 2018, 51(3): 3771-3784.
[3]	STERNIK K. Elasto-plastic constitutive model for overconsolidated clays[J]. International Journal of Civil Engineering, 2017, 15(3): 431-440. doi: 10.1007/s40999-017-0193-8
[4]	MASIN D. A hypoplastic constitutive model for clays[J]. International Journal for Numerical and nalytical Methods in Geomechanics, 2005, 29(4): 311-336. doi: 10.1002/nag.416
[5]	SHENG D, GENS A, FREDLUND D G, et al. Unsaturated soils: from constitutive modelling to numerical algorithms[J]. Computers and Geotechnics, 2008, 35(6): 810-824. doi: 10.1016/j.compgeo.2008.08.011
[6]	WHEELER S J, SIVAKUMAR V. An elasto-plastic critical state framework for unsaturated soil[J]. Géotechnique, 1995, 45(1): 35-53. doi: 10.1680/geot.1995.45.1.35
[7]	SUN De'an, SHENG D, SLOAN S W. Elastoplastic modelling of hydraulic and stress–strain behaviour of unsaturated soils[J]. Mechanics of Materials, 2007, 39(3): 212-221. doi: 10.1016/j.mechmat.2006.05.002
[8]	张玉伟, 翁效林, 宋战平, 等. 考虑黄土结构性和各向异性的修正剑桥模型[J]. 岩土力学, 2019(3): 1030-1038. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903023.htm ZHANG Yu-wei, WENG Xiao-lin, SONG Zhan-ping, et al. A modified Cambridge model considering structural and anisotropy of loess[J]. Rock and Soil Mechanics, 2019(3): 1030-1038. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903023.htm
[9]	ROUAINIA M, MUIR Wood D. A kinematic hardening constitutive model for natural clays with loss of structure[J]. Géotechnique, 2000, 50(2): 153-164. doi: 10.1680/geot.2000.50.2.153
[10]	ROSCOE K, BURLAND J. On the generalized stress–strain behaviour of wet clay[J]. Eng Plast, 1968, 3: 539-609.
[11]	HASHIGUCHI K. On the linear relations of V-lnp and ln v-lnp for isotropic consolidation of soils[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2010, 19(5): 367-376.
[12]	SHENG D, YAO Y, CARTER J P. A volume-stress model for sands under isotropic and critical stress states[J]. Canadian Geotechnical Journal, 2015, 45(11): 1639-1645.
[13]	刘艳, 赵成刚, 韦昌富. 非饱和土的修正SFG模型研究[J]. 岩土工程学报, 2012, 34(8): 1458-1463. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201208017.htm LIU Yan, ZHAO Cheng-gang, WEI Chang-fu. Research on modified SFG model of unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1458-1463. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201208017.htm
[14]	方耀宁, 郭云飞, 兰巨龙. 基于Logistic函数的贝叶斯概率矩阵分解算法[J]. 电子与信息学报, 2014, 36(3): 715-720. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201403033.htm FANG Yao-ning, GUO Yun-fei, LAN Ju-long. A bayesian probabilistic matrix factorization algorithm[J]. Based on Logistic Function Journal of Electronics & Information Technology, 2014, 36(3): 715-720. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201403033.htm
[15]	SOLTANI A, AZIMI M, DENG A, et al. A simplified method for determination of the soil–water characteristic curve variables[J]. International Journal of Geotechnical Engineering, 2017: 1-10.
[16]	SHARMA, SHYAM R. Mechanical Behaviour of Unsaturated Highly Expansive Clays[D]. Oxford: University of Oxford, 1998.
[17]	BELLIA Z, GHEMBAZA M S, BELAL T. A thermo-hydro-mechanical model of unsaturated soils based on bounding surface plasticity[J]. Computers and Geotechnics, 2015, 69: 58-69. doi: 10.1016/j.compgeo.2015.04.020
[18]	BURLAND J B, CUNNINGHAM M R, DINEEN K, et al. The mechanical behaviour of a reconstituted unsaturated silty clay[J]. Géotechnique, 2003, 53(2): 183-194.

施引文献(9)

期刊类型引用(2)

1.	谢虎，杨占杰，张伟，何超林，谢型浪，马海鑫. 基于混合蝙蝠算法的高比例风电电力系统调度方法. 可再生能源. 2023(06): 804-809 . 百度学术
2.	蔡清池，谢汉康，余剑毅. 基于固结实验推求先期固结压力合理性研究. 江科学术研究. 2020(03): 31-35 . 百度学术