层状横观各向同性地基变形问题的一个近似解

朱桂春; 史培新; 王占生

doi:10.11779/CJGE202004024

层状横观各向同性地基变形问题的一个近似解 English Version

朱桂春^{1, 2,},
史培新^1, ,,
王占生³

1.
苏州大学轨道交通学院,江苏　苏州　215000
2.
扬州工业职业技术学院,江苏　扬州　225000
3.
苏州市轨道交通集团有限公司,江苏　苏州　215000

基金项目:

国家自然科学基金项目 51778386

苏州市2018年度第十六批科技发展计划（民生科技）项目 SS201831

详细信息

作者简介:
朱桂春(1987—),男,讲师,博士研究生,主要从事地下工程设计和施工研究工作。E-mail: zhugc@ypi.edu.cn

通讯作者:
史培新, E-mail: pxshi@suda.edu.cn

中图分类号: TU433;TV642
计量
- 文章访问数: 272
- HTML全文浏览量: 29
- PDF下载量: 159
出版历程
- 收稿日期: 2019-05-21
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-03-31

Approximate solution for deformation problems of transversely isotropic multi-layered soils

1.
School of Rail Transportation, Soochow University, Suzhou 215000, China
2.
Yangzhou Polytechnic Institute, Yangzhou 225000, China
3.
Suzhou Rail Transit Group, Suzhou 215000, China

摘要

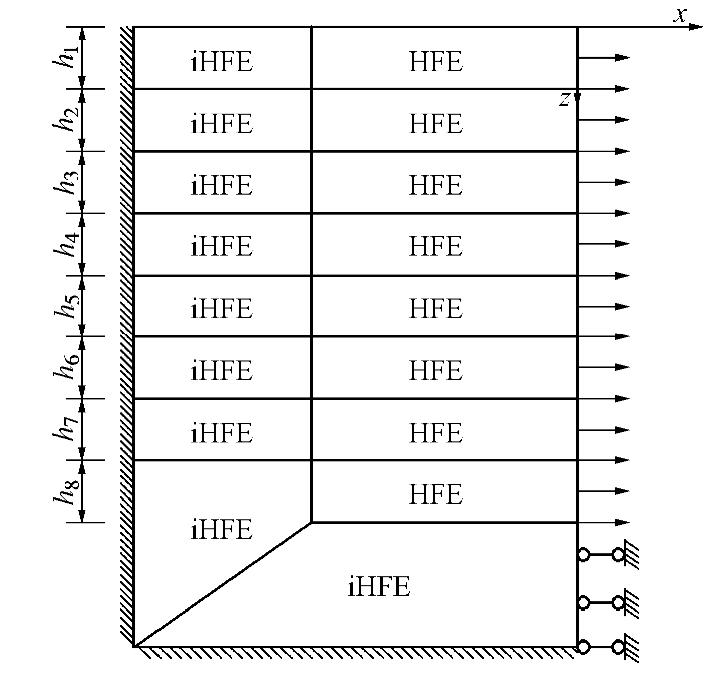
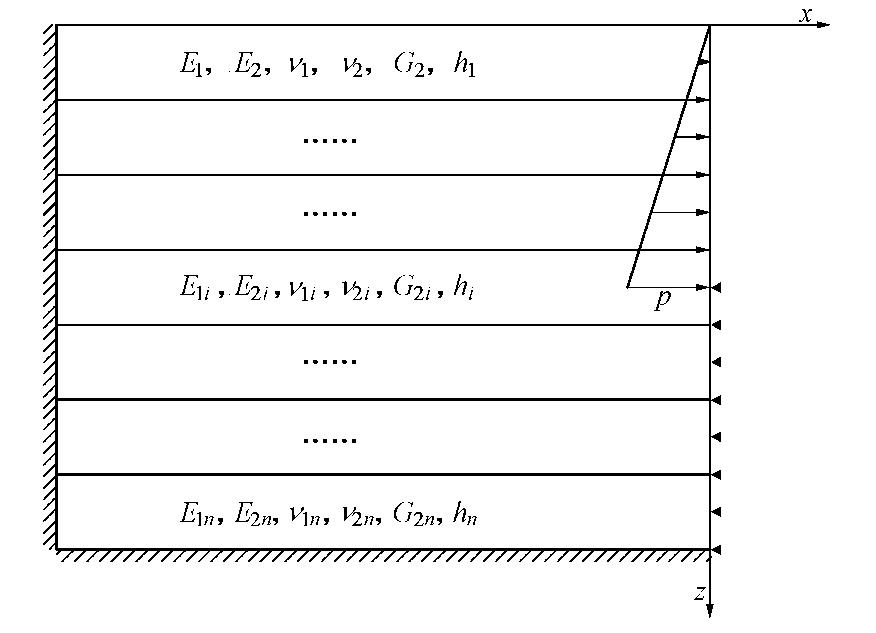
摘要: 从横观各向同性平面问题的基本弹性方程出发,利用扩展的瑞利–里兹法,将层状横观各向同性土体划分为多层有限区域及无限区域,每层土体作为一个块体,构造泛函,依据最小势能原理,对泛函进行变分求其驻值,结合边界约束条件,最终求得其近似解。求解过程采用高阶多项式及无穷坐标变换的方法实现了对无穷远处边界的高精度描述,克服了传统有限元方法对无穷远处结构盲目截断的缺点,同时又具有解析法精确求解的优点。根据公式,编制了Mathematica计算程序,得到了非对称荷载作用下层状横观各向同性地基变形的解答,并分析了横观各向同性参数和层状性质对地基变形的敏感程度,最后将其应用到某地连墙成槽施工引起的地层变形计算,研究表明该计算程序可快速简便地求解地连墙成槽施工引起的地层变形,具有较强的工程实用性。
- 横观各向同性 /
- 层状地基 /
- 瑞利–里兹法 /
- 近似解
Abstract: This study starts with the fundamental elastic equations for transversely isotropic plane problems by dividing the soil strata into a multi-layered finite region and an infinite region using the extended Rayleigh-Ritz method. Each layer of soil mass is treated as a block, and a function is constructed. The stationary values of the function are sought via the variation method in accordance with the principle of minimum potential. Boundary conditions are considered to seek the approximate solution. The solving process adopts higher-order polynomials and the transformation of infinite coordinates, achieving high accurate description of infinity boundary and overcoming the weakness of blindly truncating the infinity structures by the traditional finite element methods. A Mathematical computation program is compiled based on the formula and the solution to the plane strain problems of layered foundation under asymmetric loading is obtained. The sensitivity of the transversely isotropic parameters and layered properties to the deformation of the multi-layered soils is analyzed. Finally, it is applied to the calculation of ground deformation caused by the construction of a diaphragm wall. The research shows that the proposed program can quickly and easily calculate the ground deformation during slurry trench excavation, and is of engineering significance.
- transverse isotropy /
- layered foundation /
- Rayleigh-Ritz method /
- approximate solution

HTML全文

0. 引言

Terzaghi一维固结理论自1925年提出以来一直在工程界广泛应用。但是在饱和软黏土地区,常常发现按该固结理论预测的沉降值与实测值之间存在较大的差异,所以不断有学者对该理论进行修正。首先,Terzaghi假定土体变形是线弹性的^[1],这样土体的应力-应变关系就满足胡克定律,且不需要考虑沿深度变化的自重应力的影响。但Gibson等^[2]在研究较厚饱和黏土层固结问题时发现,考虑土体自重应力时土体的固结速率会大于Terzaghi理论值。后来,窦宜等^[3]的离心加载试验也证明考虑自重应力的必要性。因此,李冰河等^[4]考虑自重应力沿地基深度的变化,对Terzaghi一维固结理论进行了修正,并给出其半解析解。在此基础上,蓝柳和^[5]讨论了饱和黏土一维非线性流变固结问题,并指出在饱和黏土流变固结过程中考虑土体自重应力的必要性。

此外,流变性也是饱和黏性土较为显著的一种特性,也是造成饱和黏土地区固结理论预测沉降值与观测值存在较大差异的主要原因之一。因此,不断有学者试图引入不同的流变模型对Terzaghi固结理论进行改进。起初,Taylor等^[6]引入元件模型,得到了主次固结耦合的黏弹性固结理论,但此类理论为了较好地模拟试验结果（特别是加载初期）,常常需要将基本元件或基本模型进行多次组合,这就使得此类本构表达式中常常有较多参数,为求解过程增加了许多不确定的因素^[7]。另外,为考虑非线性流变的影响,一些学者^[8-11]便引入了流变经验表达式,或引入分数导数表示的弹壶元件替代传统的牛顿黏壶,或将元件模型中的一些参数视为应力或应变的函数。同时,也有学者^[12-13]通过建立土体的弹黏塑性本构关系来反映上述土体变形的时间效应,其中Yin等^[12]引入等效时间的概念,建立了一个新的弹黏塑性（EVP）本构模型,并与固结理论结合,解释了一维固结初期地基中出现的超静孔压升高现象。但柯文汇等^[13]认为等效时间模型中参考时间难以确定,于是提出了基于等黏塑性应变率线的弹黏塑性模型,虽然新建模型能够准确模拟正常固结土的固结状态,却稍微高估了超固结土的变形。近年来,姚仰平等^[14-15]基于修正剑桥模型提出统一硬化（UH）本构模型,并将其推广至考虑时间效应的弹黏塑性模型。该模型不仅能够合理描述土体大部分变形特性,且具有模型参数少、物理意义明确并且可通过常规试验确定等优点,已初步应用于一维流变固结分析中,并分析了加载初期不透水面处有效应力的松弛现象^[16]。

值得注意的是,上述研究都是在假定地基土中的渗流符合Darcy定律的基础上进行的。然而,不断有学者通过渗透试验^[17-18]证实,在饱和黏土中,孔隙水渗流存在偏离Darcy定律的现象,并分别提出了不同形式的非Darcy渗流表达式,其中应用较为广泛的当属Hansbo^[17]渗流。李传勋等^[19]、刘忠玉等^[20]基于Hansbo渗流先后考虑施工荷载及流变的影响,对Terzaghi一维固结理论进行了修正,进一步证明了考虑非Darcy渗流的必要性。随着研究的深入,纠永志等^[21]、李传勋等^[22]开始同时考虑自重应力、Hansbo渗流及变渗透系数的影响对一维固结问题进行分析,并给出了固结方程的有限差分解及半解析解。可以发现,以上考虑土体自重应力和Hansbo渗流对固结问题的研究均未考虑黏滞性的影响,而在一维固结的范畴,能够同时考虑流变性、土体自重应力、非Darcy渗流及变渗透系数的还鲜有报道。

因此,本文引入Hansbo渗流描述渗流的非Darcy特性,引入考虑时间效应的UH本构模型描述饱和黏土变形的弹黏塑性,考虑土体自重应力和变渗透系数的影响,对一维固结方程进行重新推导,并探讨土体黏滞性、自重应力、Hansbo渗流参数、地基土层厚度及外加荷载等因素对饱和黏土固结过程的影响。

1. 一维固结方程的推导

1.1 考虑时间效应的UH模型

引入文献[14, 16]所述一维情况下考虑时间效应的UH模型,其竖向应变增量 $d ε_{v}$ 的表达式为

$d ε_{v} = {\begin{matrix} \frac{(C_{s} + (C_{c} - C_{s}) \frac{M^{4}}{M_{f}^{4}}) \frac{d σ^{'}}{σ^{'}} + \frac{C_{α} d t}{t_{α} + t_{0}}}{\ln 10 (1 + e_{0})} (d σ^{'} \geq 0) \\ (\frac{C_{s} d σ^{'}}{σ^{'}} + \frac{C_{α} d t}{t_{α} + t_{0}}) / [\ln 10 (1 + e_{0})] (d σ^{'} < 0) \end{matrix} 。$

(1)

式中 $C_{c}$ 为压缩指数； $C_{s}$ 为回弹指数； $C_{α}$ 为次固结指数； $t_{0}$ 为单位时间,根据所分析的问题可取1 s,1 min等； $t_{α}$ 为老化时间； $e_{0}$ 为初始孔隙比； $σ^{'}$ 为竖向有效应力； $M$ 和 $M_{f}$ 分别为临界状态应力比和潜在破坏应力比。这些参数可表示为

$M = 6 \sin φ / (3 - \sin φ)$ ,

(2)

$M_{f} = 6 \sqrt{χ / R (1 + χ / R)} - χ / R$ ,

(3)

$(t_{α} + t_{0}) / t_{0} = R^{- α}$ ,

(4)

式中, $χ = M^{2} / [12 (3 - M)]$ , $α = (C_{C} - C_{S}) / C_{α}$ , $φ$ 为土的内摩擦角,R为超固结参数,反映了地基的超固结程度,即

$R = \exp [- \ln 10 \cdot (1 + e_{0}) ε_{v}^{p} / (C_{C} - C_{S})] σ^{'} / {p^{'}}_{c}$ 。

(5)

式中 ${p^{'}}_{c}$ 为回弹线与瞬时压缩线交点的竖向应力,当不考虑时间效应时, ${p^{'}}_{c}$ 即为先期固结压力,且与之对应的超固结参数初始值 $R_{0}$ 的倒数即为超固结比OCR； $ε_{v}^{p}$ 为竖向塑性应变,其增量 $d ε_{v}^{p}$ 可表示为

$d ε_{v}^{p} = {\begin{matrix} \frac{(C_{C} - C_{S}) \frac{M^{4}}{M_{f}^{4}} \frac{d σ^{'}}{σ^{'}} + \frac{C_{α} d t}{t_{α} + t_{0}}}{\ln 10 (1 + e_{0})} (d σ^{'} \geq 0) \\ \frac{C_{α} d t}{t_{α} + t_{0}} / [\ln 10 (1 + e_{0})] (d σ^{'} < 0) \end{matrix}$ 。

(6)

1.2 问题的描述

如图1所示,设均匀饱和黏土层厚度为H,顶面透水,底面不透水。假定饱和黏土地基中土颗粒和孔隙水自身均不可压缩,且在上覆土层荷载 ${σ^{'}}_{c z 0}$ 和自重作用下固结已经完成。现于顶面作用瞬时施加的荷载 $p_{0}$ ,这样土体的变形和孔隙水的渗流只沿竖向发生。设深度 $z$ 处,初始有效应力（即自重应力）为 ${σ^{'}}_{c z} (z)$ ,时刻 $t$ 对应的有效应力和超静孔压分别为 $σ^{'} (z, t)$ 和 $u (z, t)$ ,竖向渗流的水力梯度为 $i (z, t)$ ,渗流速度为 $v (z, t)$ ,且后二者之间的关系可用式（7）所示的Hansbo渗流公式描述：

图 1 分析模型

Figure 1. Schematic diagram of analytical model

下载: 全尺寸图片幻灯片

$v = {\begin{cases} k i {| i |}^{m - 1} / (m i_{1}^{m - 1}) (| i | \leq i_{1}) \\ k i [1 - i_{1} (m - 1) / (m | i |)] (| i | > i_{1}) \end{cases}$ 。

(7)

式中 $m$ 为试验确定的常数； $i_{1}$ 为计算渗流起始水力梯度； $i$ 为水力梯度, $i = \partial u / (\partial z \cdot γ_{w})$ ,其中 $γ_{w}$ 为水的重度； $k$ 为渗透系数,它与孔隙比e的关系用Taylor^[23]提出的经验公式描述：

$\lg k = \lg k_{0} - (e_{0} - e) / C_{k}$ ,

(8)

式中, $k_{0}$ 为与孔隙比 $e_{0}$ 对应的渗透系数, $C_{k}$ 为渗透指数。

如图1所示,在荷载 $p_{0}$ 作用下土层深度 $z$ 处的总应力和有效应力可分别表示为

$σ = σ^{'} + u_{z} = {σ^{'}}_{c z} + p_{0} + u_{0}$ ,

(9)

$σ^{'} = {σ^{'}}_{c z} + p_{0} - u$ ,

(10)

式中, $u_{z}$ 为总孔压,可表示为 $u_{z} = u + u_{0}$ ,其中 $u_{0}$ 为静孔压。

深度 $z$ 处的初始有效应力 ${σ^{'}}_{c z}$ 可表示为

${σ^{'}}_{c z} = {σ^{'}}_{c z 0} + γ^{'} z$ ,

(11)

式中, $γ^{'}$ 为土的有效重度。若令 $γ^{'} = 0$ 即视为不考虑自重应力的变化。

由渗流连续性条件可得

$\partial v / \partial z = - \partial ε_{v} / \partial t$ 。

(12)

采用与文献[19～22]同样的推导方式,即将式（1）,（7）,（8）和（10）代入式（12）可得控制方程为

$\frac{\partial}{\partial z} [ψ (γ^{'} - \frac{\partial σ^{'}}{\partial z})] = - β \frac{\partial σ^{'}}{\partial t} - η$ ,

(13)

式中, $η = γ_{w} C_{α} / [\ln 10 \cdot k_{0} (1 + e_{c z}) (t_{α} + t_{0})]$ ,

$ψ = {\begin{cases} \frac{\exp [- \ln 10 \cdot (e_{0} - e) / C_{k}]}{m {(i_{1} γ_{w})}^{m - 1}} {| γ^{'} - \frac{\partial σ^{'}}{\partial z} |}^{m - 1} (| i | \leq i_{1}) \\ \exp [- \frac{\ln 10 \cdot (e_{0} - e)}{C_{k}}] \cdot [1 - \frac{i_{1} γ_{w} (m - 1)}{m | γ^{'} - \partial σ^{'} / \partial z |}] (| i | > i_{1}) \end{cases},$

$β = {\begin{cases} \frac{γ_{w} [C_{S} + (C_{C} - C_{S}) M^{4} / M_{f}^{4}]}{\ln 10 \cdot k_{0} \cdot σ^{'} (1 + e_{c z})} (d σ^{'} \geq 0) \\ C_{S} γ_{w} / [\ln 10 \cdot k_{0} \cdot σ^{'} (1 + e_{c z})] (d σ^{'} < 0) \end{cases}$ 。

其中, $e_{c z}$ 为与 ${σ^{'}}_{c z}$ 对应的深度 $z$ 处的初始孔隙比,可表示为

$e_{c z} = {\begin{cases} e_{0} - C_{S} l g ({σ^{'}}_{c z} / {σ^{'}}_{0}) ({σ^{'}}_{c z} < {p^{'}}_{c}) \\ e_{0} - C_{S} l g \frac{{p^{'}}_{c}}{{σ^{'}}_{0}} - C_{C} l g \frac{{σ^{'}}_{c z}}{{p^{'}}_{c}} ({σ^{'}}_{c z} \geq {p^{'}}_{c}) \end{cases}$ ,

(14)

式中, ${σ^{'}}_{0}$ 为与某已知孔隙比 $e_{0}$ 对应的有效应力值,根据孔隙比 $e$ 与竖向应变 $ε_{v}$ 的关系,可得

$e = e_{c z} - ε_{v} (1 + e_{c z})$ 。

(15)

图1所示课题对应的初始条件和边界条件可分别表示为

$σ^{'} (z, 0) = {σ^{'}}_{c z 0} + γ^{'} z (0 \leq z \leq H)$ ,

(16)

$σ^{'} (0, t) = p_{0} + {σ^{'}}_{c z 0} (t > 0)$ ,

(17)

${\frac{\partial σ^{'}}{\partial z} |}_{z = H} = γ^{'} (t > 0)$ 。

(18)

2. 方程的有限体积法求解

考虑到式（13）的复杂性,欲求其解析解相当困难,故本文利用有限体积法进行求解。

2.1 方程的离散

首先以 $Δ z$ 把黏土层从上至下平均分成 $n$ 个控制容积,并在每个控制容积的中点布置一个节点；同时按给定的步长 $Δ t$ 对时间进行离散。然后在任一时间间隔 $Δ t$ （时刻t_j至t_j+1）内,在第 $b$ 控制容积内对式（13）积分：

$\begin{array}{l} \int_{t_{j}}^{t_{j + 1}} \int_{Δ z} \frac{\partial}{\partial z} [ψ (γ^{'} - \frac{\partial σ^{'}}{\partial z})] d z d t \\ = - \int_{t_{j}}^{t_{j + 1}} \int_{Δ z} (β \frac{\partial σ^{'}}{\partial t} + η) d z d t 。 \end{array}$

(19)

式（19）可改写为

$\begin{array}{l} \int_{t_{j}}^{t_{j + 1}} [{ψ (γ^{'} - \frac{\partial σ^{'}}{\partial z}) |}_{A} - {ψ (γ^{'} - \frac{\partial σ^{'}}{\partial z}) |}_{B}] d t \\ = - \int_{Δ Z} \int_{t_{j}}^{t_{j + 1}} (β \frac{\partial σ^{'}}{\partial t} + η) d t d z, \end{array}$

(20)

式中,下标A,B分别表示该控制容积的下、上边界点坐标。

对式（20）等号右边中 $σ^{'}$ 关于 $t$ 的偏导数以一阶向前差分近似,等号左边 $σ^{'}$ 关于 $z$ 的偏导数以中心差分近似,可得

$\begin{array}{l} \int_{t_{j}}^{t_{j + 1}} [ψ_{b + 1 / 2} (γ^{'} - \frac{{σ^{'}}_{b + 1} - {σ^{'}}_{b}}{Δ z}) - ψ_{b - 1 / 2} (γ^{'} - \frac{{σ^{'}}_{b} - {σ^{'}}_{b - 1}}{Δ z})] d t \\ = - β_{b}^{j + 1} ({σ^{'}}_{b}^{j + 1} - {σ^{'}}_{b}^{j}) Δ z - η_{b}^{j + 1} Δ z Δ t 。 \end{array}$

(21)

式中 $b$ 为空间节点数；j为时间离散点； $x_{b}^{j}$ 表示变量 $x$ 在 $(b - 1 / 2) Δ z$ 处, $j Δ t$ 时刻的值； $x_{b \pm 1 / 2}^{j}$ 表示变量 $x$ 在 $(b - 1 / 2 \pm 1 / 2) Δ z$ 处, $j Δ t$ 时刻的值。

然而,欲求式（21）左边的积分项,就必须要知道节点有效应力 ${σ^{'}}_{b - 1}$ , ${σ^{'}}_{b}$ , ${σ^{'}}_{b + 1}$ 在时间间隔[t_j,t_j+1]内随时间的变化关系,但这种变化关系是未知的。常规做法是用这些节点在t_j和t_j+1时刻的有效应力加权组合构成这一时间间隔内的加权平均值然后积分计算^[24]。如果取t_j和t_j+1时刻的权重分别为0和1,即为全隐格式。这样式（21）变为

$\begin{matrix} {σ^{'}}_{b}^{j + 1} = {σ^{'}}_{b}^{j} - {ψ_{b + 1 / 2}^{j + 1} [γ^{'} Δ z - ({σ^{'}}_{b + 1}^{j + 1} - {σ^{'}}_{b}^{j + 1}) - \\ ψ_{b - 1 / 2}^{j + 1} [γ^{'} Δ z - ({σ^{'}}_{b}^{j + 1} - {σ^{'}}_{b - 1}^{j + 1})]} Δ t / (β_{b}^{j + 1} Δ z^{2}) - \\ Δ t \cdot η_{b}^{j + 1} / β_{b}^{j + 1} 。 \end{matrix}$

(22)

2.2 初始条件和边界条件的处理

首先,初始条件式（16）可离散为

${σ^{'}}_{b}^{0} = {σ^{'}}_{c z 0} + (b - 1 / 2) Δ z \cdot γ^{'} (b = 1, 2, 3, \dots, n)$ 。

(23)

考虑到透水边界条件式（17）,控制容积1上边界处的有效应力梯度可近似为

${\frac{\partial σ^{'}}{\partial z} |}_{B} = \frac{{σ^{'}}_{1}^{j + 1} - (p_{0} + {σ^{'}}_{c z 0})}{Δ z / 2}$ 。

(24)

这样式（20）可离散为

$\begin{matrix} {σ^{'}}_{1}^{j + 1} = {σ^{'}}_{1}^{j} - {ψ_{1 + 1 / 2}^{j + 1} [γ^{'} Δ z - ({σ^{'}}_{2}^{j + 1} - {σ^{'}}_{1}^{j + 1})] - ψ_{1 - 1 / 2}^{j + 1} \cdot \\ [γ^{'} Δ z - 2 ({σ^{'}}_{1}^{j + 1} - p_{0} - {σ^{'}}_{cz 0})]} Δ t / (β_{1}^{j + 1} Δ z^{2}) - \\ Δ t \cdot η_{1}^{j + 1} / β_{1}^{j + 1} 。 \end{matrix}$

(25)

考虑到不透水边界式（18）,对于控制容积n,式（20）可离散为

$\begin{matrix} {σ^{'}}_{n}^{j + 1} = {σ^{'}}_{n}^{j} + ψ_{n - 1 / 2}^{j + 1} [γ^{'} Δ z - ({σ^{'}}_{n}^{j + 1} - {σ^{'}}_{n - 1}^{j + 1})] Δ t / \\ (β_{n}^{j + 1} Δ z^{2}) - Δ t \cdot η_{n}^{j + 1} / β_{n}^{j + 1} 。 \end{matrix}$

(26)

于是式（22）～（26）就构成封闭的方程组,通过迭代算法便可得到 $(j + 1) Δ t$ 时刻深度 $(b - 1 / 2) Δ z$ 处的有效应力 ${σ^{'}}_{b}^{j + 1}$ 。然后,由式（10）可得到对应的超孔隙水压力 $u_{b}^{j + 1}$ ：

$u_{b}^{j + 1} = {σ^{'}}_{c z 0} + p_{0} + (b - 1 / 2) Δ z \cdot γ^{'} - {σ^{'}}_{b}^{j + 1}$ 。

(27)

为分析土层整体孔压消散情况,这里引入按孔压定义的平均固结度：

$U_{p} = 1 - \frac{\int_{0}^{H} u (z, t) d z}{\int_{0}^{H} u (z, 0) d z} = 1 - \frac{\sum_{b = 1}^{n} u_{b}^{j + 1}}{n p_{0}}$ 。

(28)

同时,地基沉降量按下式计算：

$S_{t} = \int_{0}^{H} ε_{v} (z, t) d z = Δ z \cdot \sum_{b = 1}^{n} ε_{v b}^{j + 1}$ 。

(29)

3. UH模型适用性验证

李西斌^[25]曾基于先进GDS固结仪对萧山黏土做过一维固结试验,并将三元件模型和四元件模型引入到一维固结分析中。其后,为验证UH模型的适用性,胡晶等^[16]取试样3-4在加荷级别800～1600 kPa的试验数据,对UH模型的适用性进行了验证,却未考虑变渗透系数的影响。这里,取同样的UH模型参数,即：H=14.8 mm,e₀=0.82,C_C=0.356,C_k=0.528,C_S=0.073,C_ɑ=0.011,k₀=2.0×10^-11 m/s,M=0.984,R₀=0.575。此外,由于试样厚度较小（H=2 cm）,故可忽略Hansbo渗流和土体自重应力的影响^[22],令 $γ^{'}$ =0.0,m=1.0或i₁=0.0。然后,给出了不同流变模型下理论值与试验值的对比图,并示于图2。很明显,相比元件模型,考虑变渗透系数的UH模型结果更接近试验值,这充分印证了UH模型的适用性及考虑变渗透系数的必要性。

图 2 不同模型下沉降理论预测值与试验结果对比

Figure 2. Comparison between predicted values and experimental results of settlement theory by different models

下载: 全尺寸图片幻灯片

4. 参数分析

为便于后文进行单因素分析,这里根据文献[25]试验结果给定地基土的基本指标和计算参数为：p₀= 200 kPa, ${σ^{'}}_{c z 0}$ =50 kPa,H=10.0 m,R₀=0.5,k₀= 3.0×10^-7 m/min,M=0.772,e₀=1.5,C_C=0.45,C_k=0.75,C_S=0.08,C_α=0.03, $γ^{'} =$ 10 kN/m³,m=1.5,i₁=5.0,n=50,Δt=0.001 min,有效应力 $σ^{'}$ 的迭代误差为10^-7,此外,由于文献[21, 22, 26, 27]已对渗透指数、前期固结压力、回弹再压缩指数等参数分别讨论过,因此,这里仅对下述参数进行分析。

4.1 次固结指数C_α的影响

首先考察黏滞性对固结过程的影响。图3（a）给出不同次固结指数C_α时底部不排水边界处超静孔压随时间变化的曲线。很明显,不论是否考虑自重应力的影响,在固结的前期,当C_α=0.00（不考虑黏滞性）时孔压随时间变化曲线与时间轴平行,当C_α=0.02,0.03,0.04（考虑黏滞性）时孔压随时间变化曲线斜向上偏离了时间轴。这说明,黏滞性使不透水边界处产生了超静孔压升高的现象。且随着C_α的增大,该现象变得更为显著,孔压达到峰值的时间也更滞后。这种加载初期孔压升高现象与多维Biot固结课题中的Mandel-Cryer效应产生机理不同,因为本文讨论的课题仍属于Terzaghi一维固结理论的范畴,这里将其称为“类曼德尔效应”。实际上,Yin等^[12]、胡晶等^[16]、仇玉良等^[27]的固结分析中,也发现了该现象,并将其归因于黏土的“黏滞（蠕变）效应”或主次固结耦合机制。同时Wong等^[28]认为产生黏滞（蠕变）效应的主要机制是土颗粒周围的黏滞流,而排水路径又是影响黏滞流流动和蠕变变形的主要因素。因此,加载初期在饱和黏土地基不排水边界处,由于排水路径不通畅,土体中的水来不及排出,土颗粒周围黏滞流流动愈加缓慢,并出现拥堵,进而就会引起有效应力松弛和孔隙水压力上升。

图 3 次固结指数C_α对固结性状的影响

Figure 3. Influences of secondary compression index C_α on consolidation behavior

下载: 全尺寸图片幻灯片

此外,图3（a）还表明,考虑土体自重应力时超静孔压达到的峰值更大,但达到峰值需要的时间则大大缩短。这可从初始有效应力对渗透性的影响方面予以解释,即当考虑土体自重应力时,初始有效应力随深度的增大而增大,从由式（14）就可看出,初始有效应力越大,初始孔隙比 $e_{c z}$ 就越小,所以不透水面附近地基土的透水性就越差。因此,考虑土体自重应力时饱和黏土地基中的应力松弛现象就会更显著。

图3（b）给出了次固结指数C_α 对平均固结度U_P的影响曲线。与胡晶等^[16]曾分析过的不计土体自重应力时次固结指数对平均固结度U_P的影响类似,同一时刻平均固结度U_P随C_α的增大而减小,即随着C_α的增大,地基中超静孔压的整体消散相应滞后,考虑自重应力时也是如此。当C_α =0.00（不考虑黏滞性）时,这里得到与纠永志等^[21]一致的结论,即在加载的前期,自重应力对平均固结度U_P的影响很小,而在加载的中后期,考虑土体自重应力时平均固结度U_P却有所增大。这说明,不考虑黏滞性时,自重应力加快了加载中后期地基中超静孔压的整体消散速率。但是,当考虑黏滞性时,在加载前期,同一时刻考虑土体自重应力时平均固结度U_P 要比未考虑土体自重应力时小,而在加载的中后期却恰恰相反。即考虑黏滞性时,自重应力延缓了加载前期地基中超静孔压的整体消散速率,却加快了加载中后期地基的固结进程。

4.2 土层厚度H的影响

除上述参数的影响外,Gibson等^[2]认为对于较厚黏土层考虑土体自重应力是有必要的,李传勋等^[22]也曾分析过非达西渗流条件下地基厚度对地基固结过程的影响,但忽略了黏滞性的影响。为分析考虑土体自重应力时地基土层厚度对固结过程的影响,给出图4所示曲线。其中图4（a）给出了考虑土体自重应力和不考虑土体自重应力两种情况下,不同土层厚度时地基底部不排水面处超静孔压随时间变化的影响曲线。图4（a）表明,地基土层厚度对加载前期的“类曼德尔效应”也有影响,并且地基土层厚度越大,这一现象越显著。这与高彦斌^[9]的结论是一致的。同时,该图还表明,当不考虑土体自重应力时这一现象有所减弱。这样,二者对比就可以得到与李传勋等^[22]类似的结论,即：当土层较厚时,自重应力的影响较大；当土层较薄时土体自重应力的影响就不显著,且此时“类曼德尔效应”也不明显。这与胡晶等^[16]的结论不谋而合,即土样厚度较小（1～4 cm）是室内固结试验观察不到“类曼德尔效应”的一个重要原因。实际上,这主要是因为当土层厚度很小（排水距离很短）时,排水条件很好,因土体黏滞性引起的超静孔压异常升高的时间很短且峰值很小,固结试验中仪器就可能观测不到这种现象。

图 4 地基厚度H对固结性状的影响

Figure 4. Influences of thickness H of soil layer on consolidation behavior

下载: 全尺寸图片幻灯片

图4（b）中与李传勋等^[22]分析的现象类似,整个加载过程中,随着土层厚度的增大,同一时刻平均固结度U_P减小,即：随着土层厚度的增大,地基中整体超静孔压消散速率减慢。但是,与不考虑自重应力时相比,自重应力延滞了加载前期地基中超静孔压的整体消散的影响,却加速了加载中后期地基的固结进程。

4.3 外荷载p₀的影响

按照经典太沙基一维固结理论,地基的固结度与外荷载p₀无关,但事实上,外荷载也是决定地基固结快慢的主要因素。为探讨考虑土体自重应力条件下外荷载p₀对固结过程的影响,给出图5所示曲线。首先,为便于对比分析这里对超静孔压进行归一化处理,即U=u/p₀,图5（a）表明,外荷载p₀对“类曼德尔效应”也有影响,但与前述不同的是,在加载的前期,外荷载p₀的增大削弱了“类曼德尔效应”,并且外荷载p₀的变化对超静孔压达到峰值的时间也没有影响,同样是考虑自重应力时超静孔压达到峰值的时间被提前。这主要是因为,外荷载p₀的增大加速了孔隙水的排出,进而削弱了“类曼德尔效应”。这也与Wong等^[28]认为外荷载过大时,超固结程度较强,土样被压缩到一个稳定结构,进而就观察不到蠕变现象的结论类似。

图 5 外荷载p₀对固结性状的影响

Figure 5. Influences of external load p₀ on consolidation behavior

下载: 全尺寸图片幻灯片

图5（b）给出了外荷载p₀对平均固结度U_P的影响曲线。与李传勋等^[26]结果类似的是,随着外荷载p₀的增大,同一时刻固结度U_P增大,即：增大外荷载p₀加快了饱和黏土地基中整体超静孔压的消散速率,但此时自重应力的影响与前述分析结果一致,即自重应力滞后了加载前期地基中超静孔压的整体消散速率,却加速了加载中后期地基的固结进程。

4.4 Hansbo渗流参数的影响

纠永志等^[21]、李传勋等^[22]都曾基于Hansbo渗流并考虑土体自重应力对饱和黏土地基固结进行过分析,却都忽略了黏滞性的影响。这里给出同时考虑黏滞性时Hansbo渗流参数对饱和黏土地基固结过程的影响曲线,如图6所示。其中图6（a）,（b）分别给出了m和i₁对不排水边界处超静孔压消散的影响曲线。很显然,随着Hansbo渗流参数m和i₁的增大,加载初期超静孔压达到的峰值更大,且达到峰值需要的时间更长。也就是说,相比Darcy渗流考虑Hansbo渗流时地基排水条件更差,因此Hansbo渗流增强了“类曼德尔效应”。

图 6 m和i₁对固结性状的影响

Figure 6. Influences of m and i₁ on consolidation behavior

下载: 全尺寸图片幻灯片

图6（c）,（d）表明,与文献[19～22, 2626]结论类似的是,在加载的中后期,随着Hansbo渗流参数m和 $i_{1}$ 增大,同一时刻平均固结度U_P减小,即Hansbo渗流延缓了加载的中后期地基的固结进程,使地基中超静孔压整体消散滞后。另外,图6（c）,（d）也表明此时沿深度变化的自重应力对平均固结度U_P的影响规律和前述分析是类似的,即考虑土体自重应力延缓了固结初期整体超静孔压的消散速率,却加快了加载中后期地基土的固结速率。

5. 结论

考虑土体自重应力的影响,引入考虑时间效应的弹黏塑性本构UH模型,同时考虑Hansbo渗流及渗流过程中渗透系数变化的影响,修正了饱和黏土一维固结理论。通过与一维固结试验结果对比,验证了UH模型的适用性,并得到以下3点结论。

（1）在加载前期,土体的黏滞性使地基不透水边界附近产生了超静孔压升高的现象,且增大次固结指数、地基厚度和Hansbo渗流参数,或减小、外荷载,或考虑土体自重应力都会使该现象更加显著。

（2）考虑土体自重应力将延缓加载初期地基中超静孔压整体消散的速率,同时加快加载中后期地基的固结速率。

（3）增大次固结指数、地基土层厚度或Hansbo渗流参数,可延缓黏土地基中超静孔压整体消散的速率,而增大外荷载却可加快地基的固结进程。

图 1 横观各向同性地基分层示意图

Figure 1. Schematic drawing of transversely isotropic strata

下载: 全尺寸图片幻灯片

图 2 有限区域坐标变换

Figure 2. Coordinate transformation

下载: 全尺寸图片幻灯片

图 3 无线区域坐标变换

Figure 3. Coordinate transformation

下载: 全尺寸图片幻灯片

图 4 计算模型图

Figure 4. Computational model

下载: 全尺寸图片幻灯片

图 5 层状地基验证例水平位移比对

Figure 5. Comparison of horizontal displacement

下载: 全尺寸图片幻灯片

图 6 层状地基验证例竖向位移比对

Figure 6. Comparison of vertical displacements

下载: 全尺寸图片幻灯片

图 7 参数m对竖向位移的影响

Figure 7. Influences of m on vertical displacement

下载: 全尺寸图片幻灯片

图 8 参数m对水平位移的影响

Figure 8. Influences of m on horizontal displacement

下载: 全尺寸图片幻灯片

图 9 各工况水平位移

Figure 9. Horizontal displacements of various cases

下载: 全尺寸图片幻灯片

图 10 各工况竖向位移

Figure 10. Vertical displacements of various cases

下载: 全尺寸图片幻灯片

图 11 计算模型图

Figure 11. Computational model

下载: 全尺寸图片幻灯片

图 12 地层水平变形比对

Figure 12. Comparison of horizontal displacements

下载: 全尺寸图片幻灯片

图 13 地层竖向变形比对

Figure 13. Comparison of vertical displacements

下载: 全尺寸图片幻灯片

表 1 各地层参数表

Table 1 Soil parameters

地层编号	E₁/MPa	E₂/MPa	G₂/MPa	$ν_{1}$	$ν_{2}$	h/m
①	20	10	8.00	0.3	0.25	3
②	22	11	8.46	0.4	0.30	3
③	30	15	12.00	0.3	0.25	130

下载: 导出CSV

表 2 各地层参数表

Table 2 Soil parameters

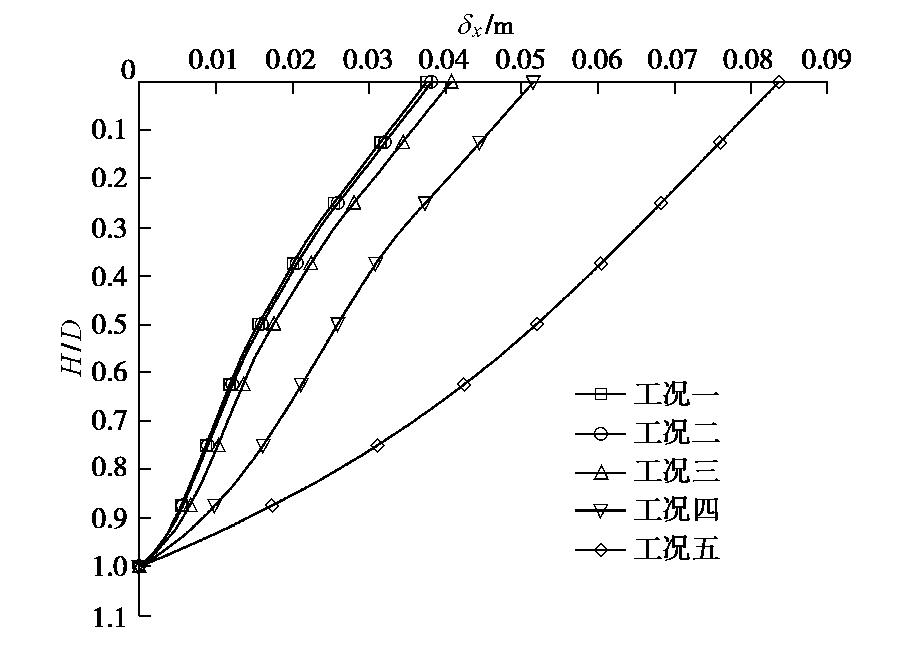
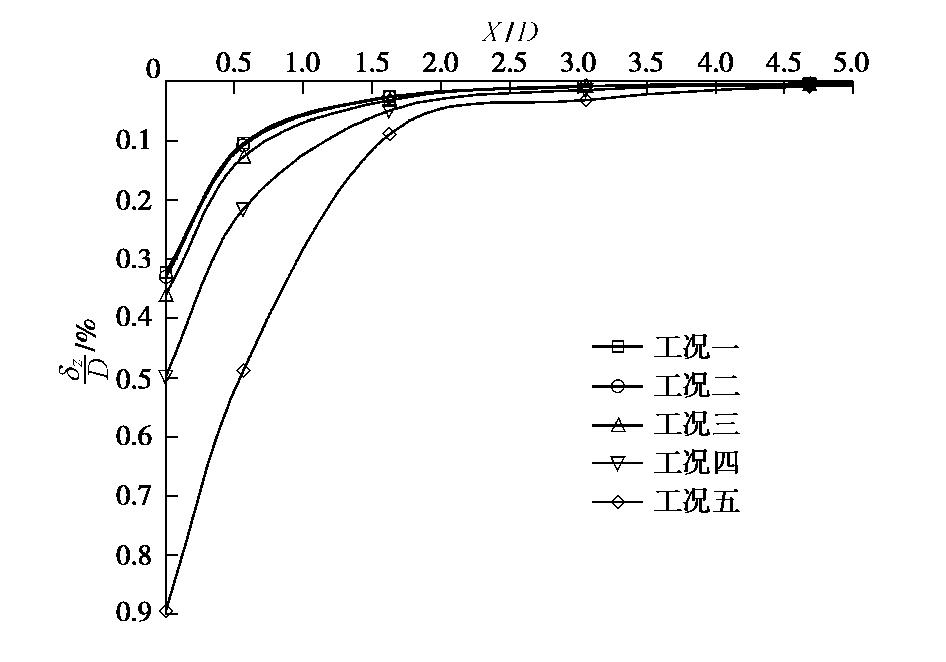
土层编号	E₁/MPa	E₂/MPa	h/m
①	2	1	2
②	6	3	2
③	16	8	2
④	25	12.5	2
⑤	30	15	4

下载: 导出CSV

表 3 各工况地层分布表

Table 3 List of soil strata

工况一	工况二	工况三	工况四	工况五
①	①	①	①	①
②	②	②	②	①
③	③	③	②	①
④	④	③	②	①
⑤	④	③	②	①

下载: 导出CSV

表 4 各地层参数表

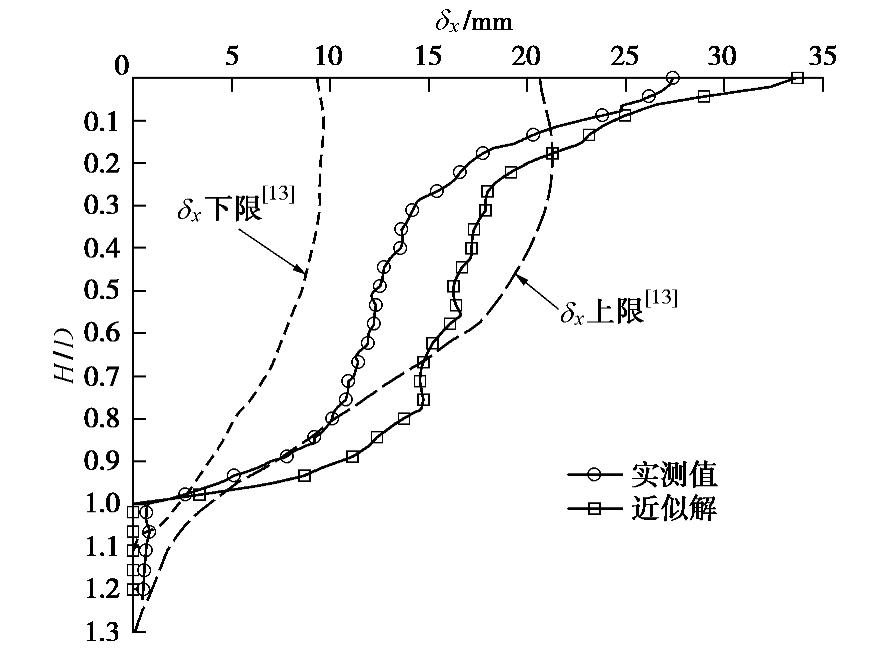
Table 4 Soil parameters

地层编号	E₁/MPa	E₂/ MPa	G₂/ MPa	$ν_{1}$ ( $ν_{2}$ )	h/ m
①	0.30	0.15	0.03	0.3	2.90
②	4.00	2.00	0.40	0.3	4.77
③	10.00	5.00	1.00	0.3	2.66
④	30.00	15.00	3.00	0.3	9.00
⑤	45.00	22.50	4.50	0.3	6.13
⑥	48.00	24.00	4.80	0.3	19.99
⑦	49.62	24.81	4.96	0.3	9.71
⑧	50.00	25.00	5.00	0.3	19.34

下载: 导出CSV

参考文献(14)

[1]	王炳军, 肖洪天, 党彦, 等. 横观各向同性地基各向异性对应力场影响研究[J]. 四川大学学报(工程科学版), 2015, 47(6): 40-48. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH201506006.htm WANG Bing-jun, XIAO Hong-tian, DANG Yan, et al. Influence of the anisotropy of a transversely isotropic foundation on additional stress fields[J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(6): 40-48. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH201506006.htm
[2]	艾智勇, 仓乃瑞, 成怡冲. 解析层元法求解层状横观各向同性地基轴对称问题[J]. 岩土工程学报, 2012, 34(5): 863-867. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201205014.htm AI Zhi-yong, CANG Nai-rui, CHENG Yi-chong. Analytical layer-element method for axisymmetric problem of transversely isotropic multi-layered soils[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(5): 863-867. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201205014.htm
[3]	李沛豪, 朱向荣. 横观各向同性弹性半空间非轴对称问题解析解[J]. 岩土工程学报, 2004, 26(3): 331-334. doi: 10.3321/j.issn:1000-4548.2004.03.006 LI Pei-hao, ZHU Xiang-rong. Analytic solution of non- axisymmetric problems in transversely isotropic elastic half Space[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(3): 331-334. (in Chinese) doi: 10.3321/j.issn:1000-4548.2004.03.006
[4]	王林生. 用柔度矩阵递推法计算横观各向同性成层地基[J]. 河海大学学报, 1989, 17(2): 104-110. doi: 10.3321/j.issn:1000-1980.1989.02.014 WANG Lin-sheng. Flexibility matrix recursion method to solve transversely isotropic multilayered soil[J]. Journal of Hohai University, 1989, 17(2): 104-110. (in Chinese) doi: 10.3321/j.issn:1000-1980.1989.02.014
[5]	HAN Ze-jun, LIN Gao, LI Jian-bo. Dynamic impedance functions for arbitrary-shaped rigid foundation embedded in anisotropic multilayered soil[J]. Journal of Engineering Mechanics, 2015, 141(11): 04015045. doi: 10.1061/(ASCE)EM.1943-7889.0000915
[6]	艾智勇, 吴超. 三维直角坐标系下分层地基的传递矩阵解[J]. 重庆建筑大学学报, 2008, 30(2): 43-46. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN200802008.htm AI Zhi-yong, WU Chao. Transfer matrix solutions of multi-layered soils in rectangular coordinate system[J]. Journal of Chongqing Jianzhu University, 2008, 30(2): 43-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN200802008.htm
[7]	AI Z Y, YUE Z Q, THAM L G, et al. Extended sneddon and muki solutions for multilayered elastic materials[J]. International Journal of Engineering Science, 2002, 40(13): 1453-1483. doi: 10.1016/S0020-7225(02)00022-8
[8]	栗振锋, 胡长顺. 横观各向同性轴对称层状弹性体系半空间问题的求解[J]. 西安公路交通大学学报, 2000, 20(4): 8-10. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200004002.htm LI Zhen-feng, HU Chang-shun. The solution of axis y metrical problems in transversely isotropic multilayered elastic half space[J]. Journal of Xi'an Highway University, 2000, 20(4): 8-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200004002.htm
[9]	陈光敬, 赵锡宏, 于立. 传递矩阵法求解成层横观各向同性弹性体轴对称问题[J]. 岩土工程学报, 1998, 20(5): 105-108. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC805.022.htm CHEN Guang-jing, ZHAO Xi-hong, YU Li. Transferring matrix method to solve axisymmetric problem of layered cross-anisotropic elastic body[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(5): 105-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC805.022.htm
[10]	巴振宁, 张艳菊, 梁建文. 横观各向同性层状半空间中凹陷地形对平面SH波的散射[J]. 地震工程与工程振动, 2015, 2(1): 9-21. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201502002.htm BA Zhen-ning, ZHANG Yan-ju, LIANG Jian-wen. Scattering of SH wave by a canyon in transversely isotropic layered half-space[J]. Earthquake Engineering and Engineering Dynamics, 2015, 2(1): 9-21. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201502002.htm
[11]	钟阳, 耿立涛. 多层弹性平面问题解的精确刚度矩阵法[J]. 岩土力学, 2008, 29(10): 2829-2832. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200810046.htm ZHONG Yang, GENG Li-tao. Explicit solution of multiplayer elastic plane by exact stiffness matrix method[J]. Rock and Soil Mechanics, 2008, 29(10): 2829-2832. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200810046.htm
[12]	艾智勇, 曾文泽. 解析层元法求解层状地基非轴对称荷载问题[J]. 岩土工程学报, 2011, 33(7): 1078-1081. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201107014.htm AI Zhi-yong, ZENG Wen-ze. Analytica layer-element method for non-axisymmetric loading problem for multi-layered soils[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(7): 1078-1081. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201107014.htm
[13]	MOHAMED A Z. Effect of Diaphragm Wall Construction on Adjacent Deep Foundation[D]. Freiberg: Technische University at Bergakademie Freiberg, 2017.
[14]	CLOUGH G W, O'ROURKE T D. Construction induced movements of insitu walls[C]//Proceedings of the ASCE Conference on Design and Performance of Earth Retaining Structures, 1990, New York: 439-470.

施引文献(10)

期刊类型引用(4)

1.	马跃，刘忠玉，张家超. 基于连续排水边界的分段线性化固结模型研究. 公路. 2024(10): 364-369 . 百度学术
2.	赵南南，邵珠山，郑晓蒙，吴奎，秦溯. 考虑锚杆作用的深埋软岩隧道黏弹塑性力学响应解析. 力学学报. 2022(02): 445-458 . 百度学术
3.	胡亚元，王啊强. 饱和孔隙-裂隙黏土双层地基的一维固结分析. 上海交通大学学报. 2022(04): 443-453 . 百度学术
4.	时刚，朱邦华，张玉蓉. 循环荷载作用下考虑Hansbo渗流的饱和黏土固结分析. 力学与实践. 2021(01): 26-37 . 百度学术