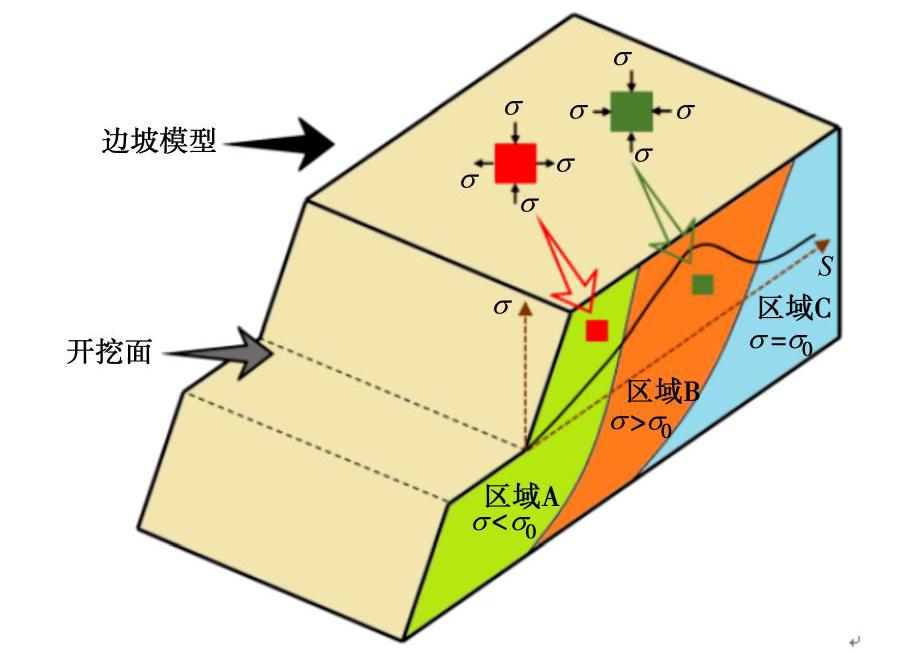
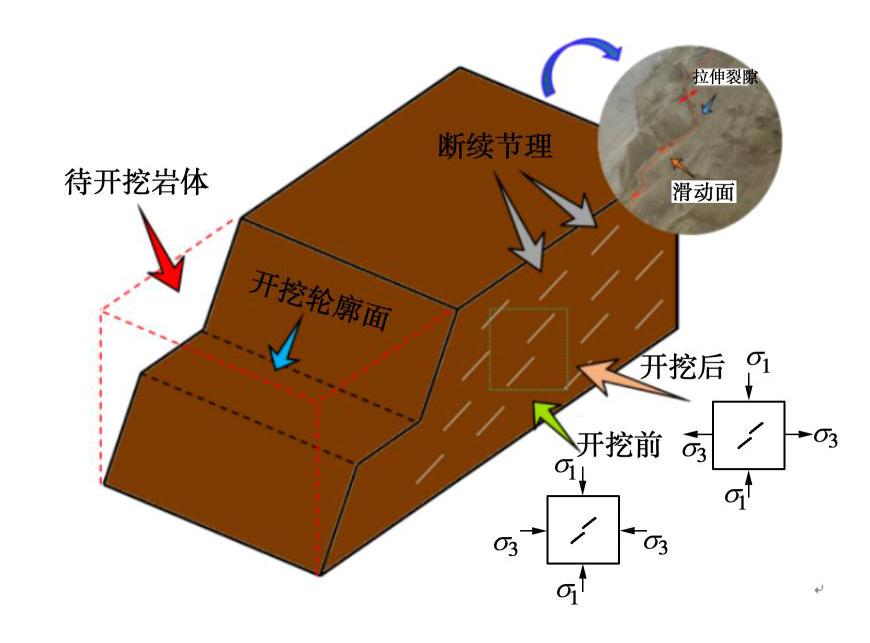
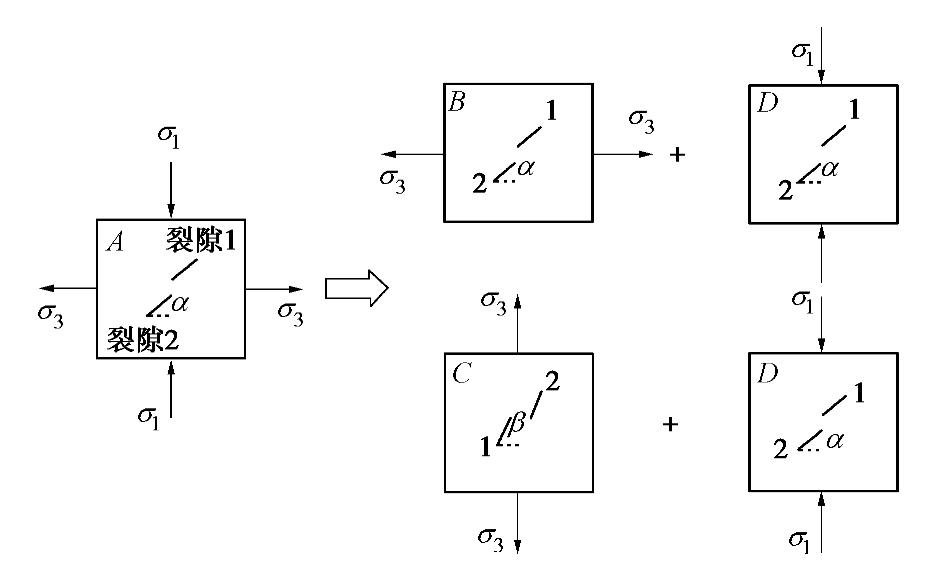
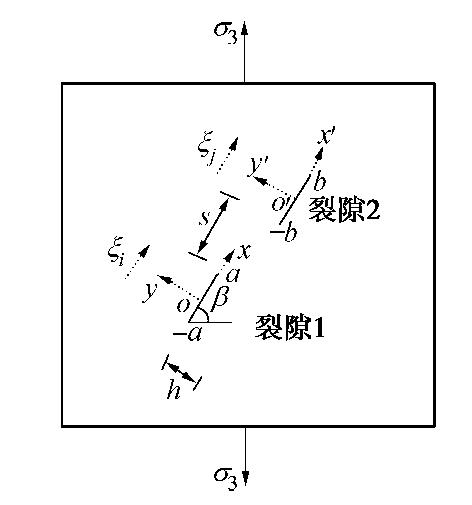
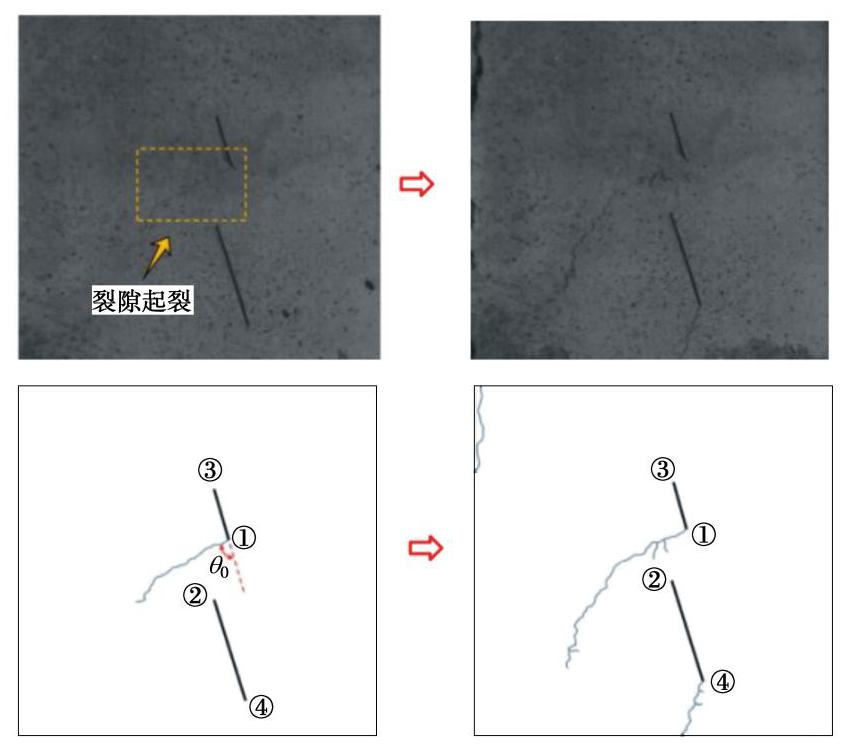
Propagation of offset parallel cracks in rock under unloading conditions
-
摘要: 岩质边坡中存在着大量的非贯通断续节理,对于开挖扰动下的边坡岩体强度及破坏模式起着重要的控制作用。为了研究边坡岩体在开挖扰动下内部节理裂隙的细观扩展规律,基于叠加原理与Kachanov法,推导了卸荷条件下平行偏置双裂隙的尖端应力强度因子表达式并从理论上分析了多种因素对裂隙间相互作用的影响规律,最后对含平行偏置裂隙的类岩试件进行了卸荷试验,结果表明:①主次裂隙间的裂隙错距或岩桥长度愈小、主裂隙长度愈大,裂隙尖端处的相互作用变化愈剧烈;②随着裂隙倾角的增大,裂隙尖端张拉破坏的趋势愈发明显,而剪切破坏趋势减弱;③裂隙间的岩桥长度越大,应力强度因子放大系数受裂隙倾角的影响越敏感。通过对比理论上不同试件在侧向卸荷条件下的裂隙轴向起裂应力与试验测得的实际起裂应力发现,两者相对误差均在4.7%以内,证明了利用提出的理论方法计算裂隙的临界起裂应力是合理可行的。通过本研究揭示的卸荷条件下平行偏置双裂隙的扩展规律,可对露天矿节理岩质边坡在开挖过程中的细观破坏机制提供一定的理论依据。Abstract: The numerous non-penetrating intermittent joints in rock slopes play an important role in controlling the strength and failure mode of rock mass under excavation disturbance. In order to determine the meso-influence laws of intermittent joint interaction in the slope under the action of excavation, using the superposition principle and the Kachanov method, the stress intensity factor of parallel offset double cracks at the tip in rock mass under unloading conditions is calculated, the influences of many factors on the interaction between cracks are theoretically analyzed, and the unloading tests on rock-like specimens with parallel offset cracks are conducted. The results show that: (1) The interaction at the crack tips becomes more severe and sensitive if the length of the main crack larger or the staggered distance between the cracks or the length of rock bridge is shorter. (2) As the inclination angle of cracks increases, the tensile failure gradually increases but shear failure weakens. (3) The sensitivity of the amplification factors of the stress intensity factor affected by the angle is positively correlated with the length of rock bridge. In addition, the axial-initiation stresses of cracks in different specimens theoretically calculated under unloading conditions are compared with the measured ones by tests, and it is found that the relative error between them are all less than 4.7%, revealing that the proposed theoretical formula is a reasonable and feasible method to calculate the axial-initiation stresses of cracks. The propagation laws of the offset parallel cracks in rock under unloading conditions are revealed and are conducive to the studies on meso-failure mechanism of jointed rock slopes in open-pit mines under the action of excavation.
-
0. 引言
近年来,为满足人们的生活需求,国家在各大城市广泛开发地下空间,如城市地铁隧道、地下商场等地下结构,其中很多都建于城市已有建筑基础下部。地震发生时地下结构由于埋置于土中且受到上部结构的影响,其受力特点和振动反应与上部建筑相比较为复杂,因此有关地下结构的抗震问题亟待解决。目前为止地震作用下地下结构与土、上部结构的相互作用理论并未成熟,在相关结构抗震设计时常常需要进行地震模拟振动台试验而提供一定试验资料。上部结构-土-隧道相互作用体系的振动台模拟试验中的一个关键问题是体系各部分之间的加速度相似比应相互匹配,因此模型土的设计至关重要。多年来国内外相关学者从物理性态、力学性态相似等方面对模型土进行设计研究:Robb等[1]为研究地震作用下某地铁-结构相互作用,以动强度为主要相似参数进行了模型土的设计,采用高岭土、膨润土、粉煤灰和水按一定比例混合模拟软黏土,试验结果达到预期强度范围;Keizo 等[2]采用原型土进行地下结构振动台试验;Hamid[3]以剪切波速作为相似指标,以高岭土,膨润土、F级粉煤灰、石灰和水混合制作模型土,用以模拟软土地基下的土-结构振动台试验;魏宝华等[4]以控制原型土的含水率和干密度来配制模型土;窦远明等[5]从物理性态相似方面考虑配制模型土,采用洗衣液、石英砂等材料,以摩擦角、黏聚力等作为相似指标;尚守平等[6]、燕晓等[7]以动剪切模量做为主要相似指标,采用在原型土里添加锯末来降低动剪切模量,其中文献[6]加速度相似比Sa的目标值为1,而实际值为4.65;文献[7]的Sa目标值为5,实际值为4.4;陈红娟等[8]基于结构与土周期相似比一致的原则,以土的卓越周期作为相似指标,场地土的卓越周期T=4h/vs,由相似理论得模型土的剪切波速比原型场地小很多,故在原型土里添加锯末以降低剪切波速,目标值SlSρ/SE=1,实际结果为0.15。
土的复杂多样性以及物理、力学性态参数较多导致模型土的配制较为困难,目前为止有关振动台动力特性试验模型土的配制方面,多数研究者[6-8]所得试验结果未能较好满足预期目标,尤其在模型土与原型土的G/Gmax-
γ 动力特性曲线的相似性方面考虑较少。本文以天津某场地粉质黏土为原型土,地勘报告见表1所示。以模型土与原型土的加速度相似比Sa应与上部结构、隧道与对应模型结构的Sa相匹配以及模型土与原型土的G/Gmax-
γ 动力特性曲线相似为目标,实施上部结构-土-隧道振动台试验模型土的设计与试验研究。表 1 天津某场地地勘报告Table 1. Geological survey report of a site in Tianjin土层类别 土层厚度d/m 埋深h/m 密度ρ/(g·cm-3) 剪切波速vse/(m·s-1) 最大动剪切模量Gmax/MPa 杂填土 3.1 3.1 1.85 132 32.23 粉质黏土 1.6 4.7 1.90 147 41.06 粉土 2.8 7.5 2.00 152 46.21 粉质黏土 3.1 10.6 1.90 168 53.63 粉质黏土 2.0 12.6 1.90 194 71.51 粉质黏土 2.0 14.6 2.00 223 99.46 粉质黏土 3.4 18.0 2.00 231 106.72 粉质黏土 7.5 25.5 2.00 240 115.20 粉土 2.6 28.1 2.00 242 117.13 粉质黏土 4.0 32.1 2.06 270 150.17 粉质黏土 2.4 34.5 2.06 285 167.32 粉质黏土 4.7 39.2 2.06 296 180.49 粉质黏土 2.8 42.0 1.99 311 192.47 1. 模型土设计
1.1 模型相似关系
上部结构-土-隧道相互作用体系振动台试验的相似关系包括:①上部结构模型、隧道模型与对应原型结构的相似;②原型场地土与模型土的相似;③上部结构模型、隧道模型与模型土的相似比的匹配。
考虑到试验的可行性,对模型进行如下相似设计:①根据振动台承载能力和台面尺寸等参数,确定上部结构、隧道和场地土模型几何相似比为1∶30;②上部结构和隧道尺寸较小,无法完全配重,且模型土与原型土加速度相似比Sa无法达到1[6-8],故采用重力失真模型;③天津地区设防烈度为8度,对应的罕遇地震加速度为0.4g,本次试验振动台最大输出加速度为1.2g,为还原罕遇地震下体系的响应情况,将振动台上部结构-土-隧道相互作用体系加速度相似比定为3。
本次振动台试验根据Buckingham
π 定理确定各物理量之间的相似关系[9]。以几何尺寸L、密度ρ和弹性模量E为基本物理量,土、上部结构及隧道的原型与对应的模型各物理量的相似比及其相似关系如表2所示。本次振动台试验是上部结构-土-隧道相互作用体系模型的动力响应试验,土的动剪切模量为土的重要动力特性参数,因此本文有关模型土的设计研究以模型土与原型土的动剪切模量比作为主要相似参数,相似关系控制方程如下:Sa=SG/SρSl。 (1) 表 2 模型相似关系Table 2. Similitude relations of model物理量 相似关系 上部结构 隧道 土 长度l [L] SL=1/30 SL=1/30 SL=1/30 线位移δ [L] Sδ=SL=1/30 Sδ=SL=1/30 Sδ=SL=1/30 弹性模量E [FL-2] SE=0.3 SE=0.265 SE=SG 等效质量密度ρe [FL-4T2] Sρe=3 Sρe=2.65 ρm/ρp 频率ω [T-1] Sω=1/ST=9.523 Sω=1/ST=9.523 9.523 时间t [T] ST=SL√Sρe/SE=0.105 0.105 0.105 加速度幅值a [LT-2] Sa=SE/(SLSρe)=3 3 SG/SρSl=3 式中,Sa,SG,Sρ,Sl为模型土与原型土的相似参数,Sa为加速度相似比,SG为动剪切模量相似比,Sρ为密度相似比,Sl为几何尺寸相似比。
1.2 相似材料
振动台试验能否真实还原地震作用下上部结构-土-隧道相互作用体系的响应取决于相似材料的选择。为使原型土与模型土满足本次试验所设定的主要相似条件,相似材料在选用方面需遵循以下原则:①应考虑选择获取方便且成本较为合理的材料;②相似材料的性质应比较稳定,在模型土配制及向模型箱装填过程中不随周围温度等环境的变化而发生变化;③模型土便于配制及振动台装填;④有关模型土与原型土动力学参数的相似比可通过改变模型土各材料的配比进行调控。
本次试验模型土与原型土的加速度相似比Sa的目标值为3,可通过降低模型土与原型土的刚质比相似系数SG/Sρ以达到目标值。通过以下方法可调节土的相关参数:①向土中掺加锯末能够降低剪切模量及密度等参数[6-8];②加入河砂能够在一定程度上调节土的G/Gmax-
γ 曲线[9];③原型土不添加其他材料配制模型土时,可通过改变土的干密度和含水率来调节土的Sρ/SG[4]。锯末与河砂这两种材料性质稳定,成本低且取材较易。本文以天津某场地粉质黏土为原型土,将粉质黏土、河砂、锯末和水按比例均匀混合以配制上部结构-土-隧道相互作用体系振动台试验所需模型土,以下简称为模型土。1.3 土体动应力-动应变非线性相似关系
文献[10]提出模型土与原型土的动应力-动应变关系的相似性是动力模型试验设计的重要因素。循环荷载作用下土体的动应力-动应变关系的骨干曲线形状最接近双曲线模型。国内外常用于描述土体骨干曲线的双曲线模型有Hardin模型、Davidenkov模型、Stokoe模型等[9]。王志佳[9]采用以上列举的3种模型对黏性土与砂性土进行拟合,通过对比分析模型的拟合参数及拟合标准差结果后得到结论:Hardin模型在拟合精度方面较差,Stokoe模型参数较少且拟合精度与Davidenkov模型较一致。本次试验土的动应力-动应变关系的双曲线模型选用Stokoe模型,其表达式为
GGmax=11+(γ/γr)α, (2) 式中,G为动剪切模量,Gmax为最大动剪切模量,
γ 为动剪应变,γr 为参考剪应变,α 为曲率系数。1.4 试验目标
(1)使上部结构-土-隧道相互作用体系各部分的原型与模型的加速度相似比相匹配,模型土与原型土的加速度相似比Sa的目标值为3。
(2)以天津某场地粉质黏土为原型土,参考天津地区不同深度土层粉质黏土的动剪应变与动剪切模量比的平均值[11],采用Stokoe模型拟合得到天津粉质黏土不同深度土层的G/Gmax-
γ 曲线。本次试验所配制模型土采用Stokoe模型拟合所得G/Gmax-γ 曲线应与天津粉质黏土相似。2. 共振柱试验
2.1 试样制作
将粉质黏土和河砂分别烘干,用木碾将粉质黏土碾碎,采用匀质干燥杨木锯末。锯末、河砂和粉质黏土分别过2 mm筛后,将粉质黏土、锯末、河砂和水按照一定质量比例混合均匀后装入密封袋中闷料24 h,闷料完成后,选用模具规格为39.1 mm×80 mm,按照土工试验方法标准[12]制样。制样完成后,将滤纸片和透水石依次贴在土样上下两端,制成土样饱和器,然后装入真空缸中进行1 h抽气,抽气完成后向真空缸中注水对试样进行饱和,饱和时间为12 h。
试验所用锯末、河砂、粉质黏土、土样及共振柱如图1所示。
2.2 试验仪器、方法与数据分析
共振柱试验是被公认为测定土力学参数最可靠的方法,美国测试与材料协会(ASTM)就将其纳入行业标准[8]。本次试验所采用仪器为河北工业大学土木工程岩土实验室的GZZ-50B型自由振动式共振柱,采用自由振动法测量模型土的有关土动力学参数。将饱和完成的土样脱模安装到共振柱上后,施加30 kPa围压固结8 h,固结完成后按照GZZ-50型共振柱仪操作说明进行共振柱试验,得到不同配比的模型土在30 kPa围压下的动剪应变、动剪切模量与阻尼比的试验数据。使用origin软件对试验数据进行处理分析,创建Stokoe模型函数,以Gmax,
γr 和α作为参数进行拟合,得到不同配比的模型土的Gmax拟合参数值及G/Gmax-γ 动力特性曲线。2.3 试配试验
为找出满足本次试验所设定相似目标的模型土的最优配比,进行了大量的试配试验。图2中的B~P代表前期试配的部分不同配比模型土的G/Gmax-
γ 曲线,Q代表原型粉质黏土的G/Gmax-γ 曲线。通过试验结果得出:由方案P的模型土(其成分锯末、河砂、粉质黏土质量比为18%∶27%∶55%,含水率为50%)所得的加速度相似比Sa等相关参数较符合所设定的相似目标。
3. 正交试验设计及结果分析
在试配试验的方案P的基础上设计并进行30 kPa围压下的模型土正交试验,以确定满足设定目标的模型土中各添加材料的最优比例,并研究各添加材料对模型土的动力学参数以及G/Gmax-
γ 动力特性曲线的影响规律。3.1 正交试验设计及部分结果
通过改变含水率,或控制锯末、河砂和粉质黏土各材料所占这三者总质量百分比可以调节模型土的部分动力学参数。选取锯末含量A、含砂量B和含水率C这3个影响因素,每种因素设置3个水平,采用正交表L9(34)确定正交方案配比组合,各方案配比及部分结果见表3所示。
表 3 正交试验方案及部分结果Table 3. Orthogonal test schemes and partial results方案 锯末A/% 河砂B/% 含水率C/% 密度ρ/(g·cm-3) 最大动剪切模量Gmax/MPa 加速度相似比Sa 1 18 21 35 1.42 9.516 3.51 2 18 27 50 1.49 8.283 2.91 3 18 33 60 1.56 6.799 2.28 4 23 21 50 1.33 9.165 3.60 5 23 27 60 1.46 7.402 2.64 6 23 33 35 1.20 8.751 3.81 7 28 21 60 1.25 6.318 2.64 8 28 27 35 1.06 6.350 3.12 9 28 33 50 1.09 6.319 3.00 注: 因素A为锯末含量,即锯末占锯末、河砂和粉质黏土总质量的百分比(m锯末/m总),因素B为河砂含量,即河砂占锯末、河砂和粉质黏土总质量的百分比(m砂/m总)。对表3中9组不同配比的模型土分别进行共振柱试验,每组模型土至少做3个试样以减小误差的影响。试验测得各组模型土在30 kPa围压下的动剪应变和对应的动剪切模量。对每组模型土的动剪切模量-动剪应变数据采用本文2.2节的数据处理方法进行拟合,得出各方案模型土的Stokoe模型相关参数及G/Gmax-
γ 曲动力特性曲线。依据相关参数评判得出模型土各添加材料的最优配比,并采用极差法和方差分析法分析各材料掺量对模型土动力特性参数的影响规律。3.2 G/Gmax-
γ 曲线相似性分析图3中m1~m9分别代表方案1到方案9的G/Gmax-
γ 动力特性曲线;p为粉质黏土即原型土的G/Gmax-γ 动力特性曲线,此曲线是由文献[11]中统计的天津地区0~50 m深度处的粉质黏土动剪应变γ 与对应的动剪切模量比G/Gmax的平均值采用Stokoe模型拟合所得。本次判定模型土与原型土G/Gmax-
γ 曲线的相似问题借鉴最小二乘法原理:将原型土拟合的Stokoe模型作为回归函数F(γr ,α),引入二元函数,见下式:Q(γr,α)=n∑i=1(Fip−Fim),Fip=GGmax=11+(γi/γpr)α,Fim=GGmax=11+(γi/γmr)α。} (3) 式中
Fip 为原型土采用Stokoe模型拟合所得剪应变(区间为10-6~10-2)下的G/Gmax值,γpr 为原型土参考剪应变;Fim 为各方案模型土采用Stokoe模型拟合所得剪应变下的G/Gmax值,γmr 为模型土参考剪应变。Q(
γr ,α )函数的直观意义是表示各方案模型土与原型土相同剪应变(区间范围为10-6~10-2)下对应的G/Gmax的距离的平方和,以下简写为Q函数。Q函数值越小,说明该方案模型土偏离原型土G/Gmax-γ 动力特性曲线程度越小。Q函数只能反映模型土与原型土动力特性曲线选取的比较点的偏离程度,不能反映出两者之间的曲线形状相似程度。而Stokoe模型中曲率系数
α 和参考剪应变γr 决定着曲线的形状,为综合考虑Stokoe模型中参考剪应变γr 和曲率系数α 对曲线相似性的影响,因此创建一个新的三元Y(Sγr ,Sα ,Q)函数:Y(Sγr,Sα,Q)=(Sγr−1)2(Sα−1)2⋅Q。 (4) 式中,
Sγr 为参考剪应变相似比,Sα 为曲率系数相似比。Sγr 值和Sα 值越接近1、Q值越小,(Sγr -1)2(Sα -1)2与Q乘积值即Y(Sγr ,Sα ,Q)函数值越小,该方案模型土与原型土的G/Gmax-γ 动力特性曲线偏离程度越小、曲线形状相似程度越高,曲线整体的相似程度就越高。Y(Sγr ,Sα ,Q)函数同时结合Q(γr ,α )函数值与Stokoe模型拟合参数值,从两个方面综合评判模型土与原型土G/Gmax-γ 动力特性曲线的相似性。由表4得方案2模型土与原型土的G/Gmax-γ 动力特性曲线相似度最高。表 4 正交方案Stokoe模型拟合参数及Q值、Y值Table 4. Fitting parameters of Stokoe model and values of Q and Y for orthogonal tests方案 参考剪应变 γr 曲率系数 α Q(γr, α) Y(Sγr, Sα, Q) P 0.00118 0.943 0 0 1 0.00174 0.925 0.033 2.71×10-6 2 0.00130 1.015 0.003 1.80×10-7 3 0.00195 0.954 0.055 3.18×10-6 4 0.00320 0.628 0.179 0.0585 5 0.00191 1.075 0.062 0.0004 6 0.00266 0.834 0.134 0.0028 7 0.00349 0.750 0.219 0.0351 8 0.00343 0.748 0.217 0.0337 9 0.00181 1.201 0.063 0.0013 注: P代表粉质黏土。3.3 加速度相似比分析
由式(1)得模型土与原型土的刚质比相似系数SG/Sρ目标值为0.1,各正交方案模型土的密度
ρ 的变化区间为1.06~1.56 g/cm3,原型土密度ρ 为2.0 g/cm3,对应的动剪切模量比SG目标值区间为0.053~0.078。由相似理论可知围压相似比应与动剪切模量相似比相等,正交方案模型土围压均为30 kPa,因此对应原型土的围压区间为385~556 kPa。根据天津场地地勘报告得该围压区间的最大动剪切模量约为115 MPa,故将各正交方案对应的原型土的Gmax定为115 MPa。由表3可知方案1、方案4与方案6的加速度相似比Sa明显偏高于目标值3,方案3、方案5与方案7的Sa低于目标值3,方案2、方案8与方案9的Sa值最为接近目标值。
3.4 各因素对试验结果影响分析
(1)极差法分析各因素对G/Gmax-
γ 曲线相似性影响极差分析法是通过对比各因素的最大值和最小值之差来分析各因素对所选指标影响问题。极差越大,说明该因素对所选指标影响越显著。以Y(Sγr ,Sα ,Q)函数值为指标,以下简写为Y函数。采用极差分析法评价锯末、河砂的含量以及含水率对G/Gmax-γ 曲线相似性的影响。极差分析结果见表5和图4。表 5 各因素对曲线相似性影响极差分析Table 5. Range analysis of influences of various factors on similitude of curves项目 因素 锯末A 河砂B 水C K1 6×10-6 0.093 0.036 K2 0.061 0.034 0.059 K3 0.070 0.004 0.035 极差 0.070 0.089 0.024 主→次 B→A→C 注: Ki为正交方案任一列上水平号为i时所对试验结果之和。a)由表5可得因素B的极差值大于因素A和因素C的极差,说明河砂含量对Y(
Sγr ,Sα ,Q)值的影响最为明显,即对模型土与原型土二者的G/Gmax-γ 动力特性曲线的相似性影响最大,其次是锯末含量,含水率对模型土与原型土动力特性曲线的相似性的影响作用最小。b)由图4可得,当模型土中的锯末含量在18%~28%之间时,锯末含量越多,Y值越大,表明模型土偏离原型土G/Gmax-
γ 曲线程度越大,导致模型土与原型土动力特性曲线的相似度越差。c)由图4可得,在一定范围内,即模型土中的河砂含量在21%~33%之间时,Y值随着河砂含量的增加而减小,模型土偏离原型土G/Gmax-
γ 的曲线程度就越小,说明河砂含量的改变能在一定程度上调节模型土的动力特性曲线,降低模型土与原型土的G/Gmax-γ 曲线之间的偏离程度,改善模型土与原型土的动力特性曲线之间的相似性。d)模型土的含水率在不同范围内变化对模型土与原型土动力曲线的相似性影响效果有所差异。从图4中可以看出当含水率在35%~50%之间时,Y值随着含水率的增加而增加,即模型土偏离原型土动力曲线的程度越大,二者相似度越差;当含水率在50%~60%时,Y值随着含水率的增加而减小,说明在此区间内含水率越高,模型土与原型土二者的G/Gmax-
γ 曲线相似程度越好。(2)方差分析法分析各材料对模型土Gmax,Gmax/
ρ 的影响规律方差分析法可用于检验有关因素对试验结果有无显著影响。以模型土的最大动剪切模量Gmax、最大动剪切模量Gmax与密度
ρ 之比Gmax/ρ 作为试验指标。在置信水平α=0.01 ,α=0.05 条件下,从F分布表查得因素显著性临界值F0.05(2,6)=5.14,F0.01(2,6)=10.92。由表6,7得出锯末含量对模型土的Gmax有显著影响,含水率对模型土的Gmax/ρ有显著影响。表 6 模型土的Gmax的方差分析Table 6. Variance analysis of Gmax of model soils项目 因素 锯末A 河砂B 水C 组间均方MSA 4.249 2.525 1.559 组内均方MSe 0.820 1.539 1.715 F值(F=MSA/Mse) 5.181 1.641 0.908 单因素显著性 显著 不显著 不显著 表 7 模型土的Gmax/ρ的方差分析Table 7. Variance analysis of Gmax/ρ of model soils项目 因素 锯末A 河砂B 水C 组间均方MSA 0.722 0.350 2.717 组内均方MSe 1.001 1.125 0.432 F值(F=MSA/Mse) 0.721 0.311 6.289 单因素显著性 不显著 不显著 显著 3.5 综合判定模型土最优配比
本次试验关于模型土与原型土的相似性判定标准如下:
(1)由表4可知正交试验方案2的模型土与原型土的G/Gmax-
γ 曲线在相同剪应变下(区间范围为10-6~10-2)对应点的动剪切模量比G/Gmax的距离的平方和即Q值等于0.003,Y值等于1.80×10-7,均为各正交方案中的最小值,Q值越小说明两曲线距离越近,Y值越小说明两曲线形状越接近。故方案2的模型土与原型粉质黏土的动力特性曲线最相似。(2)本次试验模型土与原型土的加速度相似比Sa目标值为3,方案2的Sa值为2.9,接近目标值3。
综合判定得出方案2为本次试验模型土的最优方案,模型土各材料锯末、河砂和粉质黏土所占固体颗粒总质量的比例为18%锯末27%砂55%粉质黏土,含水率为50%。
4. 不同围压下模型土的验证
为进一步验证方案2模型土是否满足不同围压下与对应深度处原型土的G/Gmax-
γ 动力特性曲线的相似性,以及不同围压下模型土与原型土的加速度相似比Sa是否满足预期目标值3,对方案2模型土另外进行了50 kPa与70 kPa围压下的共振柱试验。由表8可知加速度相似比Sa在2.54~2.9之间,与目标值3较为接近。由图5及表9可知不同围压下的模型土与对应深度的原型土的G/Gmax-
γ 动力特性曲线基本相似:3个围压下的Sγr ,Sα 值都接近1,Q值在0.003~0.007之间,Y值在1.11×10-7~8.44×10-7之间,说明两曲线的形状相似、距离接近,可认为曲线相似。方案2基本满足不同围压下本次试验所设定模型土与原型土的相似目标,确定作为本次上部结构-土-隧道模型振动台试验所用模型土。表 8 模型土与原型土的加速度相似比相关参数Table 8. Correlation parameters about similitude ratio of acceleration of model and prototype soils类别 围压σ/kPa 最大动剪切模量Gmax/MPa 加速度相似比Sa 原型土 402 115 2.9 模型土 30 8.3 原型土 670 150 2.76 模型土 50 10.3 原型土 940 192 2.54 模型土 70 12.0 表 9 模型土与原型土G/Gmax-γ 曲线相似性相关参数Table 9. Correlation parameters about similitude of G/Gmax-γ of model and prototype soils类别 围压σ/kPa 参考剪应变γr 曲率系数α Q Y 原型土 402 0.00106 0.945 0.003 8.44×10-7 模型土 30 0.00130 1.015 原型土 670 0.00127 0.961 0.004 1.68×10-7 模型土 50 0.00134 1.074 原型土 940 0.00136 0.935 0.007 1.11×10-7 模型土 70 0.00139 1.104 另外,阻尼比也是土的动力特性中的一个重要参数,由于它是无量纲量,所以模型土和原型土应该具有相同的阻尼比
λ 随剪应变γ 的变化关系曲线[6]。原型土的阻尼比
λ 随剪应变γ 变化的λ -γ 曲线由天津地区不同深度土层粉质黏土的动剪应变与阻尼比的平均值[11]拟合得到,最优配比模型土在不同围压下的λ -γ 曲线由每组试样进行共振柱试验得到的所有数据拟合所得。由图6可得最优配比模型土与原型土在不同围压下的
λ -γ 曲线趋势相同:阻尼比λ 都随着剪应变γ 的增大而增大,两者的阻尼比随着剪应变的增大都逐渐趋于定值。两者λ -γ 曲线的形状虽有一定差别,但是整体的变化趋势基本一致,最优配比模型土与原型土的阻尼比-剪应变曲线相似度尚可。5. 卓越周期相似分析
抗震设计中,场地的卓越周期对结构的地震响应影响较大[8,13]。根据相似理论,土的卓越周期相似比应与上部结构及隧道的周期相似比一致,可基于土的卓越周期相似的原则设计模型土[8, 13-14]。
为进一步保证设计的方案2模型土与原型土在地震响应时的相似性,需比较方案2模型土与原型土的卓越周期相似系数ST是否达到预期目标值0.105。
由天津场地地勘报告可得原型场地土的剪切波速随深度不断变化,故采用等效剪切波速计算原型土的周期。
T=4h/vse ,vse=d0/t ,t=n∑i=1di/vsi。} (5) 式中,h为总土层厚度,vse为土层等效剪切波速(m/s),d0为计算深度(m),t为剪切波在地面至计算深度之间的传播时间,di为计算深度范围内第i土层的厚度(m),vsi为计算深度范围内第i土层的剪切波速(m/s),n为计算深度范围内土层的分层数。
根据式(5)计算得到天津原型场地土的等效剪切波速vse为214.998 m/s,卓越周期T为0.781 s。根据方案2模型土在不同围压下的最大动剪切模量值,代入式(6)[15],采用origin软件拟合得到式(6)中的系数k与n的值(如图7),即可以得出模型土在不同围压下的Gmax计算公式。
Gmax=k⋅pa(σ3pa)n, (6) 式中,k,n为常数,
σ3 为围压,pa 为大气压力,等于1.01×105 Pa。模型土深度根据模型箱深度取1.4 m,围压为
σ=ρgh=1.49×10×1.4=20.86 kPa。 (7) 按模型箱深度将模型土分为14层,模型土的等效剪切波速计算式如下:
vse=h/t ,t=∫h0dxvs=∫h0dx√Gmax/ρ。} (8) 根据式(6),(8)及采用origin软件拟合得到式(6)中的系数k与n的值,编程计算得到方案2模型土的等效剪切波速为82.285 m/s,卓越周期为0.068 s,故方案2模型土与原型土的卓越周期相似比为0.087。卓越周期相似比预期目标为0.105,表明本次研究所得模型土与原型土不仅与结构体系保持一致的加速度相似比,在G/Gmax-
γ 动力特性曲线和卓越周期方面也具有较高的相似性。6. 结论
本文以天津某场地粉质黏土为原型土,基于土与上部结构、下部隧道加速度相似比一致的原则,设计了一种以锯末、河砂、粉质黏土和水为成分的模型土;对不同配比的模型土进行共振柱试验,找到满足设计目标的较优配比模型土,并以此为基础进行正交试验,研究得出各添加材料对模型土有关动力参数的影响规律;同时验证了不同围压下最优配比的模型土与原型土是否满足设定的相似目标,并且对比探讨了模型土与原型土关于阻尼比的相似性;并基于土、上部结构与隧道周期相似比一致的原则验证了模型土与原型土的卓越周期相似性。本次试验为今后有关振动台模型土的配制研究提供了一定的参考。主要结论有:
(1)本文试验采用Stokoe模型拟合参数,同时引入Q(
γr ,α )函数,创建三元Y(Sγr ,Sα ,Q)函数,从Stokoe模型拟合参数值、Q函数值和Y函数值三方面综合判定得出正交试验方案2的模型土与原型土的G/Gmax-γ 动力特性曲线最为相似,且其与原型土的加速度相似比非常接近Sa等于3的相似目标,由此将其确定为最优配比模型土,作为本次关于上部结构-土-隧道振动台试验所需模型土。最优配比方案模型土材料中锯末、河砂与粉质黏土质量比为18%∶27%∶55%,含水率为50%。(2)模型土中的河砂含量对模型土与原型土的G/Gmax-
γ 的动力曲线相似性影响程度最大,其次是锯末含量,含水率对二者的动力曲线相似性影响最小。3种材料的添加对G/Gmax-γ 动力特性曲线的调节范围较广,对其它土质的G/Gmax-γ 曲线也可以通过添加并调节锯末、河砂的含量及含水率进行模型土的配制。(3)模型土中锯末含量对最大动剪切模量Gmax影响显著,锯末掺量越多,Gmax越小,但同时Y值越大,导致模型土G/Gmax-
γ 动力特性曲线偏离原型土较多,二者的动力曲线相似性越差;含水率对模型土的Gmax/ρ值有显著影响,可在一定范围内改变含水率以调节原型土与模型土的加速度相似比。(4)进行了不同围压下方案2模型土的共振柱试验,进一步验证了不同围压下最优配比的模型土满足本次试验的预期相似目标。
(5)同时对比探讨模型土与原型土关于阻尼比的相似性,得出二者的
λ -γ 曲线趋势大致相同,二者的阻尼比相似度尚可。(6)基于土、隧道与上部结构周期相似比一致的原则,采用土的卓越周期相似系数验证模型土与原型土的相似性,计算所得结果为0.087,与目标值0.105较为接近,表明本次研究所得模型土与原型土关于卓越周期方面有较好的相似性。
-
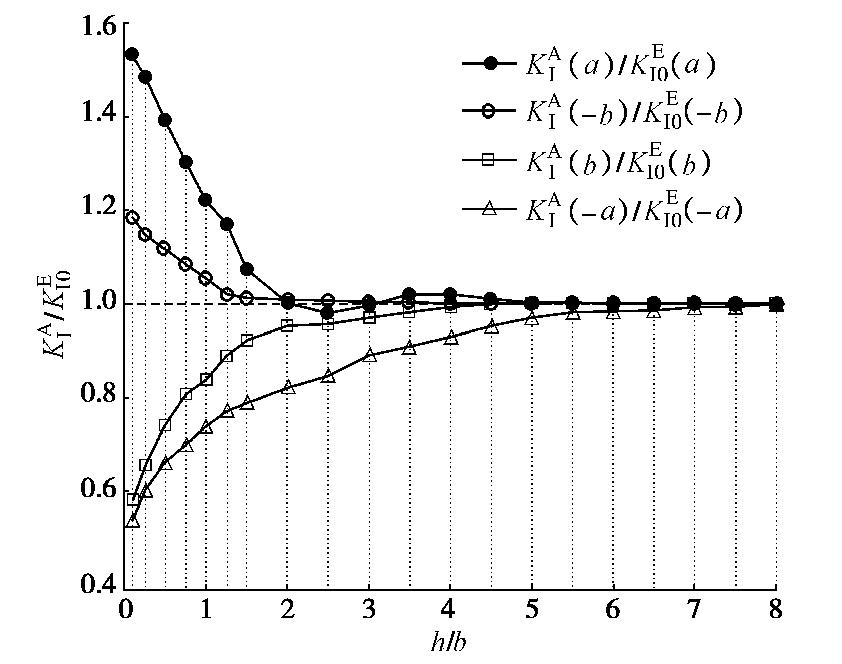
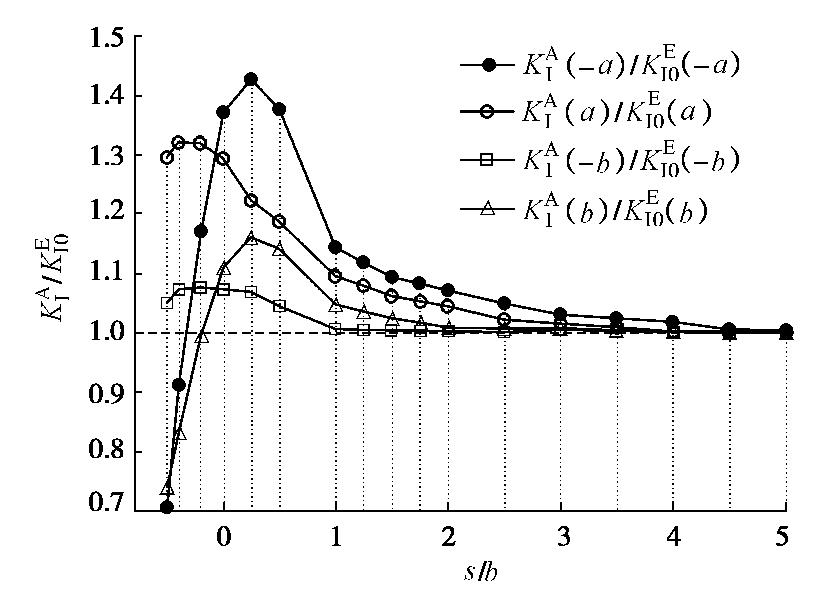
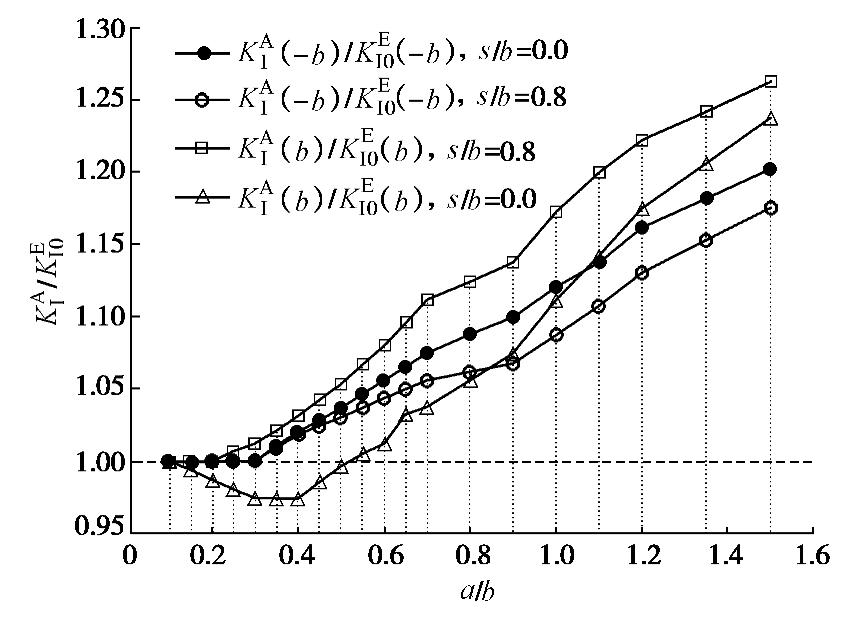
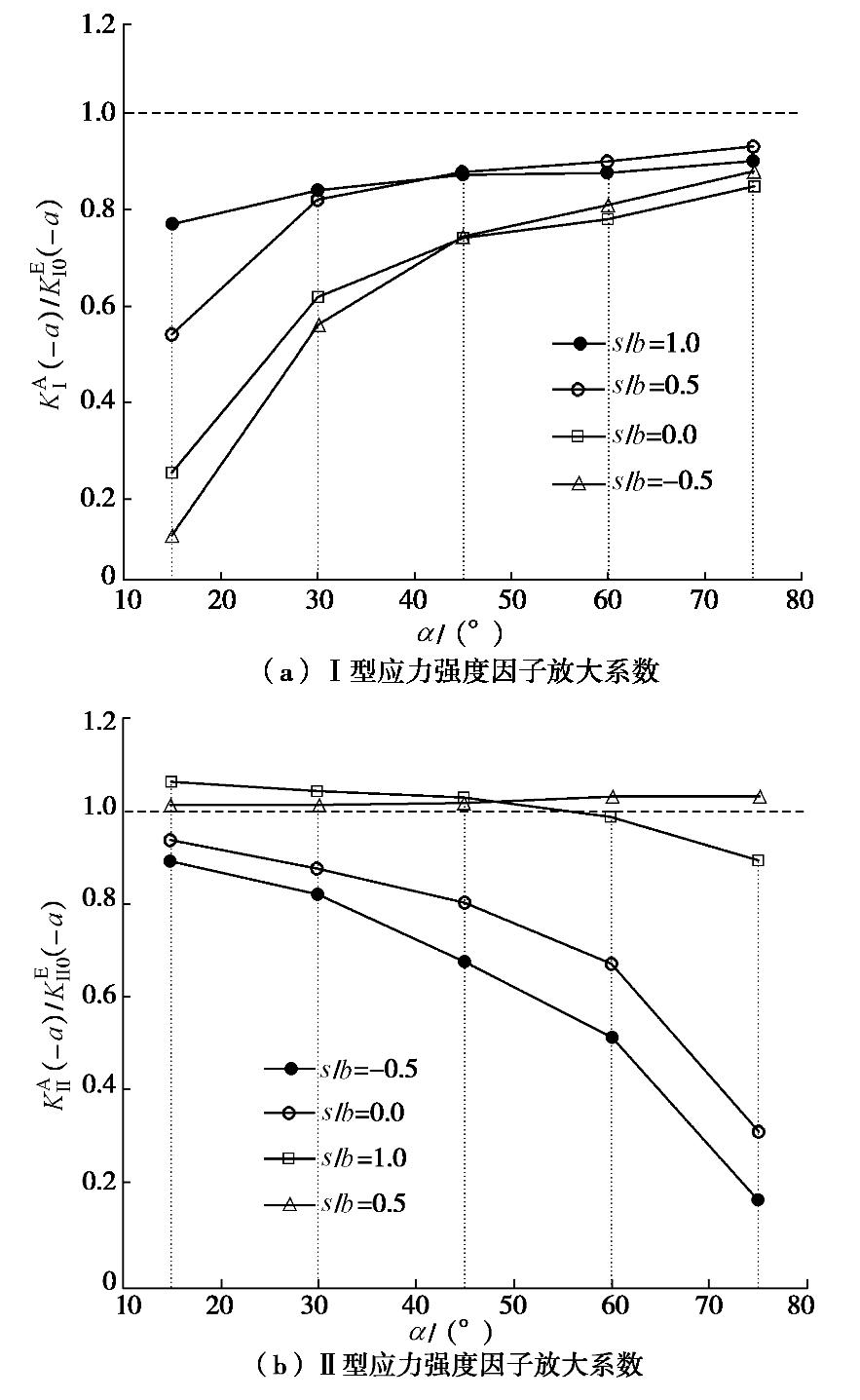
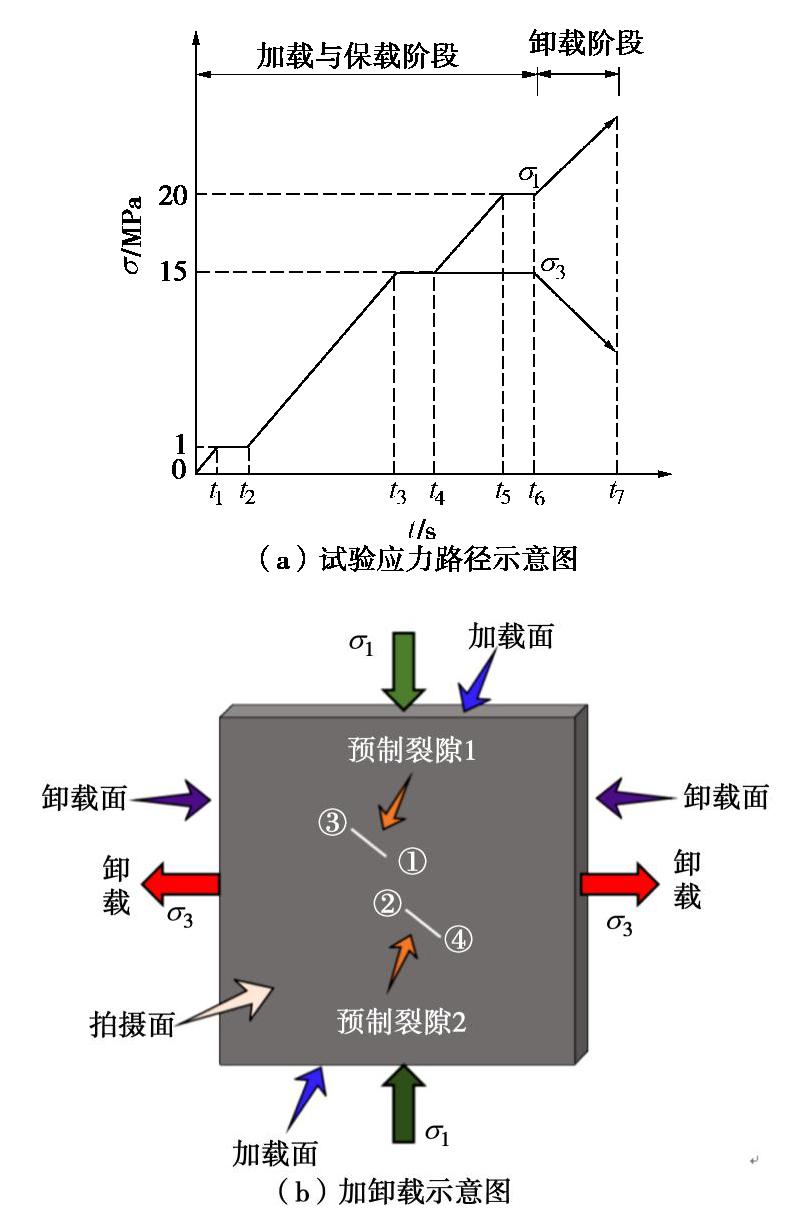
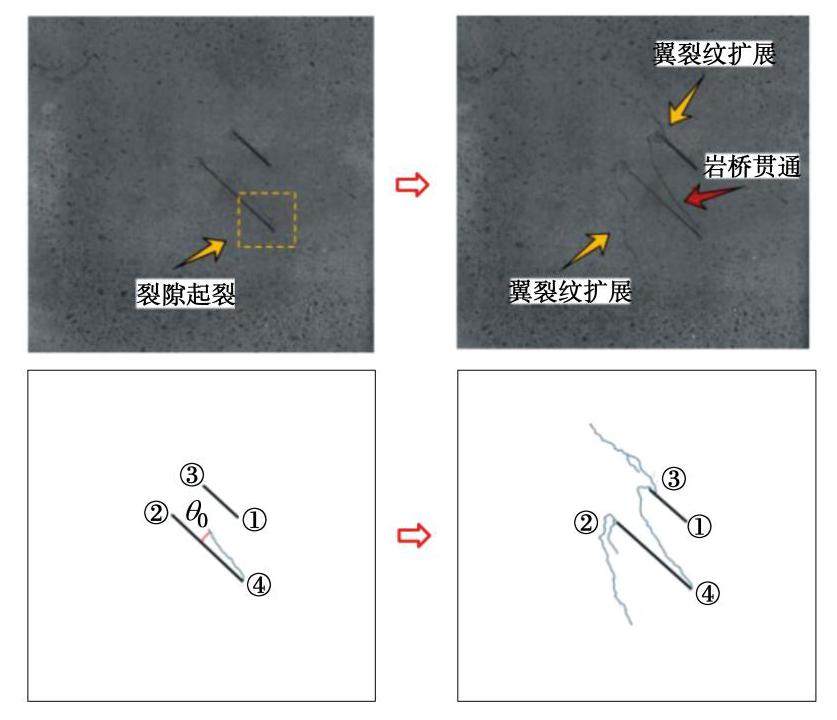
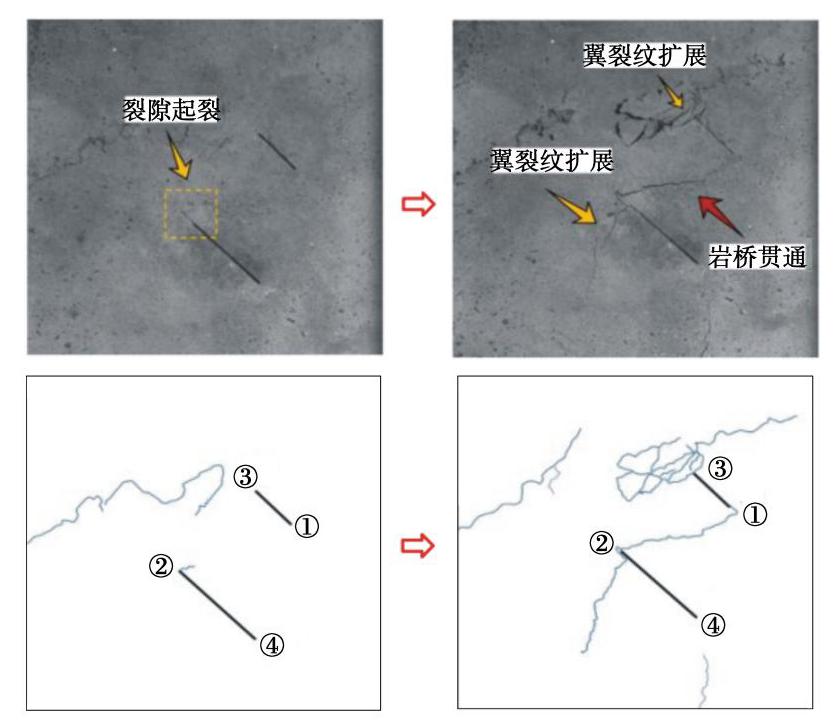
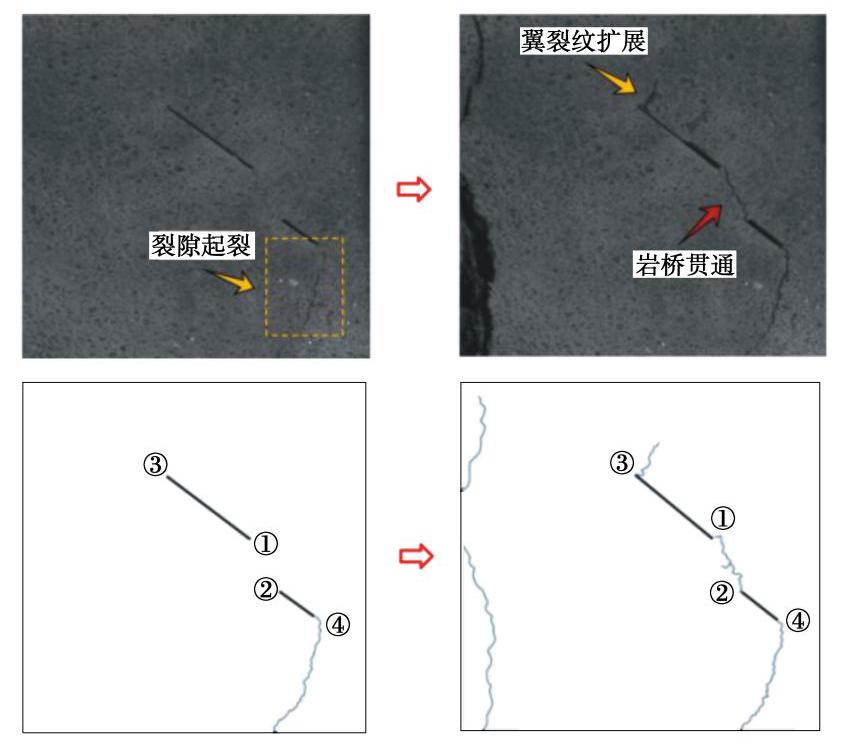
表 1 应力强度因子放大系数误差分析
Table 1 Error analysis of amplification factors of SIF
s/a 本文(B) 手册(C) 相对误差值 KΙ(−b)/KΙ0(−b) KΙ(b)/KΙ0(b) KΙ(−b)/KΙ0(−b) KΙ(b)/KΙ0(b) KΙ(−b)/KΙ0(−b) KΙ(b)/KΙ0(b) -0.5 0.8577 1.1237 0.8700 1.1380 0.0623 0.0143 -0.25 0.9966 1.1287 1.0100 1.1400 0.0534 0.0113 0 1.1098 1.1214 1.1210 1.1320 0.0182 0.0106 0.25 1.1662 1.1063 1.1700 1.1120 0.0138 0.0057 0.5 1.1715 1.0891 1.1730 1.0900 0.0015 0.0009 注: 相对误差W1=|C−B| ,s/a 为负值代表裂隙之间有重叠。表 2 砂岩与试件的力学参数对照表
Table 2 Mechanical properties of sandstone and specimens
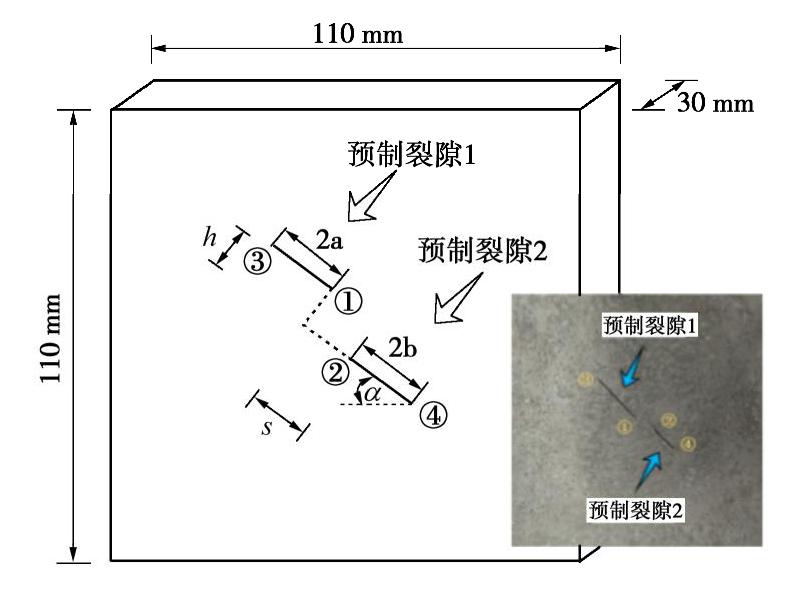
材料 密度/(kg·m-3) 单轴抗压强度/MPa 单轴抗拉强度/MPa 弹性模量/GPa 泊松比 砂岩 2000~2600 20 ~ 200 4 ~ 25 10 ~ 100 0.2 ~ 0.3 试件 2350 52.32 5.06 15.21 0.23 表 3 试件中裂隙的相关几何参数
Table 3 Geometric parameters of cracks in specimens
试件编号 裂隙倾角α/(°) 裂隙1长度2a/ mm 裂隙2长度2b/mm 岩桥长度s/mm 裂隙错距h/mm 1 45 12 24 -12 6 2 45 12 24 -12 12 3 45 12 24 -12 24 4 45 12 24 12 6 5 45 12 36 12 6 6 30 12 24 12 6 7 75 12 24 12 6 注: s为负值时代表裂隙之间存在搭接部分。表 4 卸荷条件下不同试件的裂隙轴向起裂应力
Table 4 Axial-initiation stresses of cracks in different specimens under unloading conditions
试件编号 起裂位置 理论轴向起裂应力σ1t/kN 实际轴向起裂应力σ1s/ kN 相对误差W2/% 1 主裂隙外尖端 89.03 85.17 4.5 2 主裂隙内尖端 93.16 89.71 3.8 3 主裂隙内尖端 96.11 92.13 4.3 4 次裂隙外尖端 85.64 83.52 2.5 5 次裂隙内尖端 83.25 79.68 4.5 6 主裂隙内尖端 86.22 82.33 4.7 7 次裂隙内尖端 97.17 94.28 3.1 注: W2=|σ1t−σ1s |/σ1s 。 -
[1] HUANG D, CEN D F, MA G W, et al. Step-path failure of rock slopes with intermittent joints[J]. Landslides, 2015, 12(5): 911-926. doi: 10.1007/s10346-014-0517-6
[2] TANG C A, LIN P, WONG R H C, et al. Analysis of crack coalescence in rock-like materials containing three flaws—Part II: Numerical approach[J]. International Journal of Rock Mechanics & Mining Sciences, 2001, 38(7): 925-939.
[3] BOBET A, EINSTEIN H H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(7): 863-888. doi: 10.1016/S0148-9062(98)00005-9
[4] WONG R H C, CHAU K T. The coalescence of frictional cracks and the shear zone formation in brittle solids under compressive stresses[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(3): 335.
[5] 杨圣奇. 断续三裂隙砂岩强度破坏和裂隙扩展特征研究[J]. 岩土力学, 2013, 34(1): 31-39. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201301004.htm YANG Sheng-qi. Study of strength failure and crack coalescence behavior of sandstone containing three pre-existing fissures[J]. Rock and Soil Mechanics, 2013, 34(1): 31-39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201301004.htm
[6] 赵程, 鲍冲, 田加深, 等. 基于应变局部化的双裂纹岩样贯通模式及强度试验研究[J]. 岩石力学与工程学报, 2015, 34(11): 239-2318. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201511015.htm ZHAO Cheng, BAO Chong, TIAN Jia-shen, et al. Experimental study of coslescence mode of cracks and strength of rock with double flaws based on strain localization[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(11): 2309-2318. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201511015.htm
[7] 黄达, 金华辉, 黄润秋. 拉剪应力状态下岩体裂隙扩展的断裂力学机制及物理模型试验[J]. 岩土力学, 2011, 32(4): 997-1002. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201104005.htm HUAND Da, JIN Hua-hui, HUANG Run-qiu. Mechanism of fracture mechanics and physical model test of rocks crack expanding under tension-shear stress[J]. Rock and Soil Mechanics, 2011, 32(4): 997-1002. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201104005.htm
[8] 刘磊, 贾洪彪, 马淑芝. 考虑卸荷效应的岩质边坡断裂损伤模型及应用[J]. 岩石力学与工程学报, 2015, 34(4): 747-754. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201504011.htm LIU Lei, JIA Hong-biao, MA Shu-zhi. A fracture damage model for rock slopes under unloading and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(4): 747-754. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201504011.htm
[9] 黄润秋. 岩石高边坡发育的动力过程及其稳定性控制[J]. 岩石力学与工程学报, 2008, 27(8): 1525-1544. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200808004.htm HUANG Run-qiu. Geodynamical process and stability control of high rock slope development[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1525-1544. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200808004.htm
[10] 何庆芝, 郦正能. 工程断裂力学[M]. 北京: 北京航空航天大学出版社, 1993. HE Qing-zhi, LI Zheng-neng. Engineering Fracture Mechanics[M]. Beijing: Beihang University Press, 1993. (in Chinese)
[11] KACHANOV M. A simple technique of stress analysis in elastic solids with many cracks[J]. International Journal of Fracture, 1985, 28(1): 11-19.
[12] 席婧仪, 陈忠辉, 朱帝杰, 等. 岩石不等长裂纹应力强度因子及起裂规律研究[J]. 岩土工程学报, 2015, 37(4): 727-733. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201504023.htm XI Jing-yi, CHEN Zhong-hui, ZHU Di-jie, et al. Stress intensity factors and initiation of unequal collinear cracks in rock[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(4): 727-733. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201504023.htm
[13] 中国航空研究院. 应力强度因子手册(修订版)[M]. 北京: 科学出版社, 1996: 38-39. Chinese Aeronautical Establishment. Handbook of Stress Intensity Factors (Revised Edition)[M]. Beijing: SciencePress, 1996: 38-39. (in Chinese)
[14] 宋彦琦, 李名, 王晓, 等. 基于高速摄影的双预制裂纹大理岩加卸载试验[J]. 岩石力学与工程学报, 2015, 34(增刊1): 2679-2689. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2015S1012.htm SONG Yan-qi, LI Ming, WANG Xiao, et al. Experimental test on marble containing two pre-existing cracks under loading and unloading conditions based on high-speed photography[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 2679-2689. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2015S1012.htm
[15] 范天佑. 断裂理论基础[M]. 北京: 科学出版社, 2003: 73-100. FAN Tian-you. Theoretical Basis of Fracture[M]. Beijing: Science Press, 2003: 73-100. (in Chinese)
-
期刊类型引用(2)
1. 谢军,李延涛,宗金辉,黄久鹏. 斜交隧道—土体相互作用体系振动台试验设计. 科学技术与工程. 2022(17): 7165-7173 .  百度学术
百度学术
2. 李平,刘应慈,周楷,朱胜,李玉影. 振动台模型试验相似设计综述. 防灾科技学院学报. 2020(04): 29-35 .  百度学术
百度学术
其他类型引用(12)



 下载:
下载: