考虑抗拉强度剪断的非饱和土无限边坡稳定性分析

李梦姿; 蔡国庆; 李昊; 杨贝贝; 赵成刚

doi:10.11779/CJGE202004013

考虑抗拉强度剪断的非饱和土无限边坡稳定性分析 English Version

李梦姿^{1, 2,},
蔡国庆^{1, 2, ,},
李昊³,
杨贝贝⁴,
赵成刚^{1, 2}

1.
城市地下工程教育部重点实验室,北京　100044
2.
北京交通大学土木建筑工程学院,北京　100044
3.
河南省交通运输厅,河南　郑州　450003
4.
北京城建设计发展集团股份有限公司郑州分公司,河南　郑州　450000

基金项目:

国家自然科学基金项目 51722802

国家自然科学基金项目 U1834206

国家自然科学基金项目 51678041

河南省交通运输厅科技计划项目 2017B4

详细信息

作者简介:
李梦姿(1992—),女,博士研究生,主要从事非饱和土力学相关研究工作。E-mail: mzli118@163.com

通讯作者:
蔡国庆, E-mail: guoqing.cai@bjtu.edu.cn

中图分类号: TU432
计量
- 文章访问数: 337
- HTML全文浏览量: 49
- PDF下载量: 272
出版历程
- 收稿日期: 2019-03-14
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-03-31

Stability of infinite unsaturated soil slopes with tensile strength cut-off

LI Meng-zi^{1, 2,},
CAI Guo-qing^{1, 2, ,},
LI Hao³,
YANG Bei-bei⁴,
ZHAO Cheng-gang^{1, 2}

1.
Key Laboratory of Urban Underground Engineering of Ministry of Education, Beijing Jiaotong University, Beijing 100044, China
2.
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
3.
Bureau of Transport of Henan Province, Zhengzhou 450003, China
4.
Zhengzhou Branch of Beijing Urban Construction Design& Development Group Co., Ltd., Zhengzhou 450000, China

摘要

摘要: 基于Fredlund强度理论提出了抗拉强度包线部分截断的非饱和土非线性强度准则（C-F准则）。该准则允许土体破坏过程中产生剪切破碎。然后建立无限边坡在稳定渗流作用下,考虑抗拉强度部分剪断的无限边坡稳定性分析方法框架,给出非线性强度包线下安全系数的求解方法。该方法可以考虑抗拉强度部分剪断和渗流作用对边坡稳定性的影响规律。分析结果表明,C-F准则较Fredlund强度准则所得安全系数会有降低,对渗流高陡非饱和土边坡稳定性分析的影响会更加显著。
- 非饱和土 /
- 无限边坡 /
- 抗拉强度 /
- 剪断
Abstract: Based on the Fredlund strength theory, a nonlinear strength criterion for unsaturated soils is proposed. The tensile strength envelope of the Fredlund strength theory as a result of extrapolation of compressive tests into the tensile regime is partially truncated or eliminated in the new strength criterion. The new tensile strength cut-off criterion (C-F criterion) allows to construct the failure mechanisms including rupture mode and shear deformation mode. Then a generalized framework for the stability of infinite slopes under steady unsaturated seepage conditions is put forward using the C-F criterion, and a uniform expression for the safety factor under nonlinear strength criterion is given. The influences of tensile strength cut-off and seepage on slope stability can be considered. The results show that the stability factors for infinite slopes in unsaturated soils with tensile strength cut-off are reduced compared to those based on the Fredlund strength envelope, with the largest drop for steep slopes particularly subjected to heavy rainfall infiltration.
- unsaturated soil /
- infinite slope /
- tensile strength /
- cut-off

HTML全文

0. 引言

土质边坡稳定性受地形地貌、降雨、土性和水文地质条件等多种因素的影响。其中,土性即边坡材料的强度是最重要的影响因素。经典的分析方法通常采用对材料拉剪强度预测比较精确的Mohr–Coulomb强度准则^[1-3]。近年来,随着对土体非饱和强度特性研究的深入,土体的非饱和强度特性对地下水位线以上的浅层边坡稳定性发挥着重要作用,非饱和土强度理论逐渐用于边坡稳定性分析中^[4-5]。Fredlund双应力变量强度理论,能够很好地描述非饱和土在不同基质吸力下非饱和土三轴试验的压剪强度,且具参数少物理意义明确的特点,被广泛用于非饱和土边坡稳定性分析中^[5-6]。

降雨入渗诱发的滑坡可能发生在地下水位以上的非饱和土中,通常具有平行于坡面的浅滑面^[7],而分析该类滑坡通常采用无限边坡模型。无限边坡模型虽然是一种几何形状简单的平面应变问题的简化模型,且忽略了应力集中,但实践表明用于浅层边坡稳定性分析是有效的^[8]。许多学者以无限边坡为分析对象,例如马忠武等^[9]进行降雨入渗时无限边坡的水平位移与稳定性分析；王俊等^[10]研究基于无限边坡算法的降雨型滑坡预警系统的模型试验；唐小松等^[11]在研究不完备概率信息条件下边坡可靠度分析方法时也采用了无限边坡。研究中均未考虑抗拉强度对无限边坡的影响,也很少有学者将非饱和土拉–剪耦合强度理论用于无限边坡稳定性分析。

抗拉强度是影响土坝、边坡、公路路堤等土体结构抗拉开裂和后续抗拉破坏的关键因素^[12]。Abd等^[13]和Michalows等^[14]指出在边坡失稳过程中由于坡体对坡顶后缘的拉张作用,可能在滑坡过程中产生张拉破坏裂缝,汤连生等^[15]通过模型试验观察到在边坡失稳过程中产生了拉裂缝,并指出滑坡的破坏面是由张拉和剪切破坏面组合而成的。因此,抗拉强度应作为滑坡机制的一部分,在拉–剪耦合破坏模式下评价边坡稳定性。

土体作为散粒体材料,其抗拉强度较小,容易受到扰动,且受试验条件限制,在实验室很难精确地测定复杂应力条件下土的抗拉强度,难以得出完整的抗拉强度包络线。在经典的边坡稳定性分析中遇到抗拉强度的问题,经常预先设置拉裂缝并假定土体不能承受拉力或者采用外推法,将压剪试验的强度包线反向延长至拉应力区。

对于非饱和土,抗拉强度主要由颗粒间的胶结作用、范德华力、双电层的吸附作用和毛细作用组成（非饱和特性）^[16],毛细作用包括由基质吸力（或负孔隙水压力）引起的毛细管力和由润湿液体表面张力作用于空气–水界面而引起的毛细管力^[12]。毛细作用力通常从湿砂土中的千帕到黏性土中的几千千帕不等,毛细作用对黏结效应的重要贡献,使非饱和土的表观黏聚力增加,在增加土体抗剪强度的同时抗拉强度也随之增大,其对强度的贡献不容忽略。

目前研究非饱和土抗拉强度的试验,通常为不同基质吸力下的直接拉伸试验^[16]和三轴伸长试验^[17],而对于多向拉伸应力状态的强度,大多是通过拟合单轴抗拉强度和三轴压缩强度得到拉压剪耦合强度包络线^[18-19],复杂应力条件下的多向拉伸抗拉强度是通过内插得到的,具有很大的不确定性,且非饱和土拉剪耦合强度的影响因素较多,表达式较为复杂且不统一,不便于应用。然而,Fredlund双应力变量强度理论外推得到的抗拉强度又明显高估了土的抗拉强度,使边坡稳定性分析偏于不安全。

本文采用直接减少或者部分剪断Fredlund强度理论拉应力区强度包线的方法,即在平面应变问题中拉应力区的强度包络线为某个莫尔圆的一部分（C-F强度理论）。并根据该强度理论建立了稳定渗流作用下无限边坡稳定性分析方法框架,给出了该非线性强度理论下安全系数的求解方法,研究抗拉强度的不同处理方法和渗流作用,对非饱和土无限边坡稳定性的影响。

1. 抗拉强度部分剪断准则

Fredlund 等^[20]建立的基于双应力状态变量的非饱和土的抗剪切强度表达式为

$τ_{f} = c^{'} + {(σ - u_{a})}_{f} \tan φ^{'} + {(u_{a} - u_{w})}_{f} \tan φ^{b}$ ,

(1)

式中, $τ_{f}$ , ${(σ - u_{a})}_{f}$ 和 ${(u_{a} - u_{w})}_{f}$ 分别为非饱和土剪切面上的剪切强度、净法向应力和基质吸力,σ为总应力,u_a为孔隙气压力,u_w为孔隙水压力, $c^{'}$ 为有效黏聚力, $φ^{'}$ 为有效内摩擦角, $φ^{b}$ 为与基质吸力有关的摩擦角。

Fredlund双应力变量强度理论,当基质吸力为0时,即为经典的Mohr–Coulomb强度准则,单轴抗拉强度和抗压强度可分别表示为 $f_{t} = 2 c^{'} \cos φ^{'} /$ (1+cos $φ^{'}$ ),f_c=2 $c^{'} \cos φ^{'}$ /(1-cos $φ^{'}$ )；各向同性拉伸强度为f_3t= $c^{'} \cos φ^{'}$ ；当基质吸力为s时,强度包线为一簇平行于Mohr–Coulomb强度包线的直线,单轴抗拉强度和抗压强度可分别表示为f_t=2ccos $φ^{'}$ /(1+cos $φ^{'}$ )和f_c=2ccos $φ^{'}$ /(1-cos $φ^{'}$ ),各向同性拉伸强度为f_3t=ccot $φ^{'}$ ,其中c=c′+(u_a-u_w)tanϕ^b为非饱和土表观黏聚力。

试验结果和研究^[21-22]表明该强度准则在低应力的压剪区域能较好地描述土体的抗剪强度。但对拉剪区强度的描述,是根据土的压缩试验结果外推到拉伸状态得到的,大于试验所测得的抗拉强度^[19]。而且土体作为散粒体材料,很难进行多向拉伸状态的试验,许多复杂应力的抗拉强度试验实际是围压增加或轴压减小的伸长试验^[17],这并非严格意义的抗拉强度试验。从理论上讲土体多向受拉时,产生裂缝损伤的概率变大,其各向同性抗拉强度应低于土体的单轴抗拉强度。受试验条件和土体易变性的影响,土体的抗拉强度具有很大的不确定性。

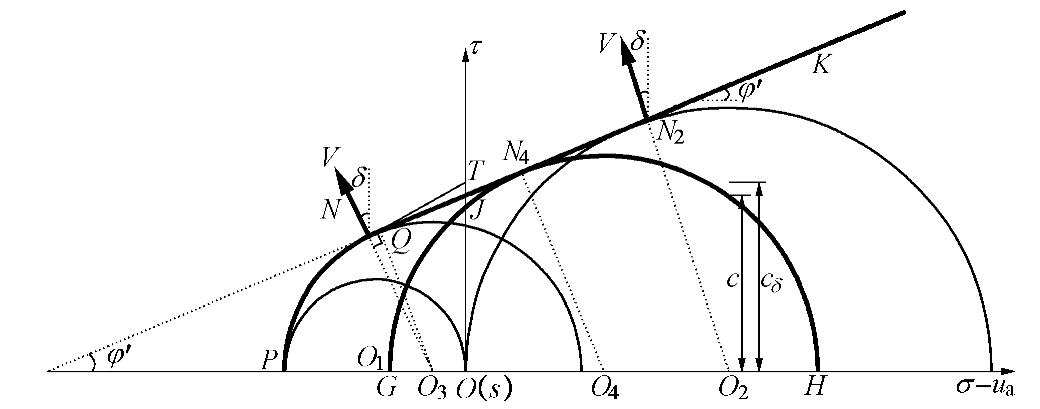
在未考虑材料的非饱和特性时（基质吸力为0）,Paul^[23]提出了在Mohr–Coulomb准则中,限制拉伸状态容许拉应力的方法并给出了图示表达。即在三维主应力空间的拉应力区,采用平行于应力轴、大小相等且相互垂直的3个平面与原始的M–C准则组成新的考虑抗拉强度部分剪断的强度准则。该模型认为土体的各向同性拉伸和单轴抗拉强度相等。这实际上是由三维主应力空间Galileo-Rankine最大拉应力准则和M–C准则的组合。在平面应变状态,该屈服准则的强度包络线在压剪应力区为原始M–C准则的直线部分,在拉剪应力区为某个极限莫尔圆的部分圆弧。拉剪应力区和压剪应力区的分界点为两者的切点。本文将此法延伸到非饱和土中,考虑对Fredlund强度理论的抗拉强度部分剪断（cut-off）,为表达方便,这个新的准则记为C-F准则,在平面应变状态如图1所示。强度面为一个平滑的曲面PP′K′K；在压剪区,为极限状态莫尔圆及其公切线组成的平面QQ′K′K；在拉应力区,部分剪断的单轴抗拉强度由O′P′（饱和）和OP（基质吸力为s）表示,强度面为曲面P′Q′QP,是由不同基质吸力下的一簇极限莫尔圆的部分圆弧组成。

图 1 平面应变C-F准则

Figure 1. Strength envelope of C-F criterion

下载: 全尺寸图片幻灯片

当基质吸力为s时,取QP部分的任一点N,作切线TN,其倾角为δ,在相关联流动法则中, $δ$ 为剪胀角；Reynolds^[24]和Park等^[25]认为与拉力相关的变形为土体间的断裂和分离,因此 $δ$ 为破裂角（rupture angle）,该定义更符合拉力作用下土体变形的实质；但在求解安全系数时,为给出解析表达式,本文参考Mohr–Coulomb准则中压剪强度区内摩擦角的定义,认为δF为拉剪强度区的内摩擦角。 $δ$ 的取值范围为ϕ′≤δ<90°。与文献[26]中拉剪强度内摩擦角大于压剪强度内摩擦角一致。为给出在部分剪断抗拉强度的非线性C-F准则的下无限边坡的安全系数,把与倾角 $δ$ 相对应的 $τ$ 轴的截距OT定义为拉剪区黏聚力,记为 $c_{δ}$ ,但这里的c_δ不能解释为拉应力作用下的真正黏聚力,只是与压剪区黏聚力相对应的表达。

取Fredlund强度理论中抗拉强度的一部分作为土体部分剪断后的抗拉强度。

$O P = f_{t} = ζ \frac{2 c \cos φ^{'}}{1 + \sin φ^{'}} (0 \leq ξ \leq 1)$ 。

(2)

当ζ为0时,完全忽略非饱和土体的抗拉强度；当其为1时,与Fredlund双应力变量强度理论的抗拉强度相同。

根据几何关系可得强度包线非线性段弧QP的方程为

$\frac{{(σ^{'} - r + f_{t})}^{2}}{r^{2}} + \frac{τ^{2}}{r^{2}} = 1$ ,

(3a)

式中, $σ^{'} = σ - u_{a}$ ,r为弧QP的半径,

$r = c \frac{1 + (1 - 2 ζ) \sin φ^{'}}{\cos φ^{'}}$ ,

(3b)

$O T = c_{δ} = \frac{r (1 - \sin δ)}{\cos δ} + f_{t} \tan δ$ ,

(3c)

代入r和 $f_{t}$ 可得

$c_{δ} = c [\frac{1 + (1 - 2 ζ) \sin φ^{'}}{\cos φ^{'}} \frac{(1 - \sin δ)}{\cos δ} + ζ \frac{2 \cos φ^{'}}{1 + \sin φ^{'}} \tan δ]$ 。

(4)

令

$B = \frac{1 + (1 - 2 ζ) \sin φ^{'}}{\cos φ^{'}}$ ,

(5)

$C = ζ \frac{2 \cos φ^{'}}{1 + \sin φ^{'}}$ ,

(6)

因此：

$c_{δ} = [c^{'} + (u_{a} - u_{w}) \tan φ^{b}] [B \frac{(1 - \sin δ)}{\cos δ} + C \tan δ]$ 。

(7)

赵成刚等^[27]根据功的表达式推出了非饱和土有效应力表达式：

$σ^{'} = σ - [S_{r} u_{w} + (1 - S_{r}) u_{a}] = σ - u_{a} + S_{r} (u_{a} - u_{w})$ ,

(8)

式中,S_r为非饱和土有效饱和度。当采用式（8）的有效应力作为计算非饱和土抗剪强度的状态变量时,存在以下关系式：

$\tan φ^{b} = S_{r} \tan φ^{'}$ 。

(9)

因此：

$c = c^{'} + (u_{a} - u_{w}) S_{r} \tan φ^{'} = c^{'} + M \tan φ^{'}$ ,

(10)

式中,

$M = (u_{a} - u_{w}) S_{r}$ 。

(11)

对于同一层土,当给定ζ和 $φ^{'}$ 时,B和C为常数,C-F强度准则的包络线是确定的。

因此,考虑抗拉强度部分截断的非饱和土C-F准则可表示为下列形式：

$τ_{f} = c_{δ} + σ^{'} \tan δ (φ \leq δ < 90 °)$ 。

(12)

当ζ=1时,δ= $φ^{'}$ ,式（12）变为 $τ_{f}$ =c+ $σ^{'} \tan φ^{'}$ ,即为Fredlund强度理论；当0≤ζ<1时,式（12）为C-F准则,若δ= $φ^{'}$ ,极限应力状态处于C-F准则的线性段c_δ=c,若δ> $φ^{'}$ ,极限应力状态处于C-F准则的非线性圆弧段。

2. 无限边坡稳定性

2.1 非饱和土无限边坡稳定性

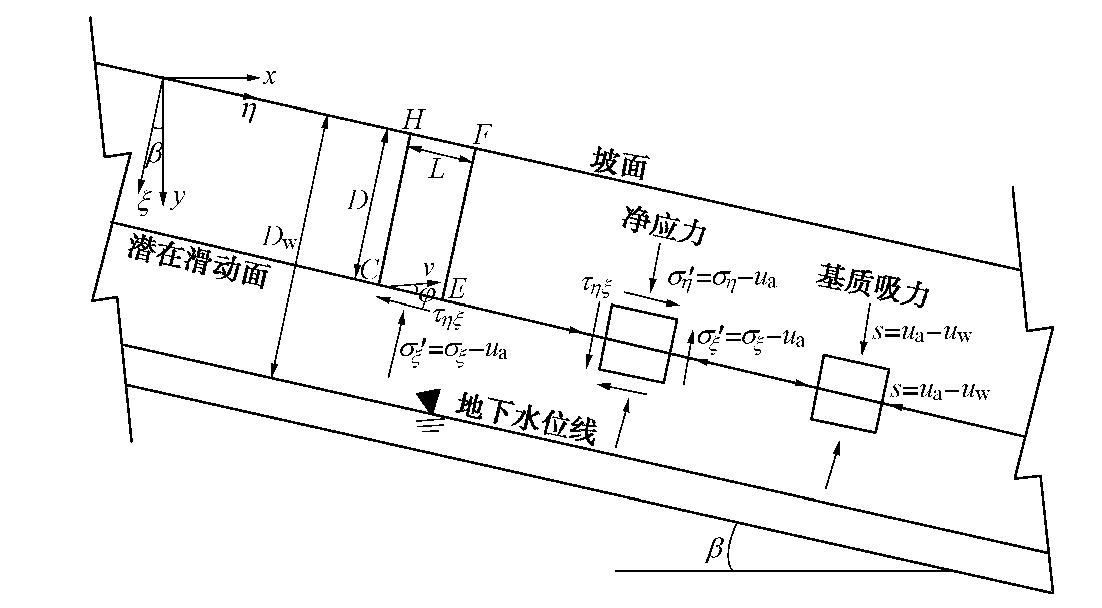
无限边坡模型假定潜在滑动面上应力是均匀分布的,整个滑坡面的应力状态可以用相同的莫尔圆表示,而且由于这种滑坡一般具有离地表较近的浅层滑动面,应力状态莫尔圆离强度准则的原点较近,其破坏可能受拉剪强度准则控制,如图2的GO₄H圆。如引言所述,在非饱和土边坡中,降雨入渗通常引起浅层边坡失稳。因此,无限边坡模型被认为是分析非饱和土边坡稳定性比较常用的模型。图3为平面应变状态浅层无限斜坡模型示意图。设无限边坡的倾角为 $β$ ,x轴和y轴分别沿着水平方向和竖直方向。η和ξ分别是沿x轴和y轴顺时针旋转 $β$ 的轴。假设潜在滑动面和地下水位线均平行于坡面,距离坡面分别为D和D_w且D < D_w。

图 2 C-F准则截面（吸力恒定）

Figure 2. Cross section of C-F criterion (constant matrix suction)

下载: 全尺寸图片幻灯片

图 3 无限斜坡模型示意图

Figure 3. Schematic diagram for shallow infinite slope model

下载: 全尺寸图片幻灯片

潜在滑动面的正应力 $σ_{ξ}$ 和剪应力 $τ_{ξ η}$ 可以通过平衡微分方程和边界条件得到：

$σ_{ξ} = γ D \cos β$ ,

(13a)

$τ_{ξ η} = γ D \sin β$ ,

(13b)

式中,D为潜在滑动面的厚度, $γ$ 为坡体的平均重度, $β$ 为坡角。

由极限平衡法安全系数的定义：

$F = \frac{τ_{f}}{τ}$ ,

(14)

代入非饱和土抗剪强度公式（12）可得

$\begin{array}{l} F = \frac{τ_{f}}{τ} = \frac{c_{δ} + (σ_{ξ} - u_{a}) \tan δ}{τ_{ξ η}} \\ {^{_{^{}}}}_{} = \frac{\tan δ}{\tan β} + [\frac{c^{'} + S_{r} (u_{a} - u_{w}) \tan φ^{'}}{γ D \sin β}] [B \frac{(1 - \sin δ)}{\cos δ} + C \tan δ] 。 \end{array}$

(15)

方程（15）右侧第一项是由土的内摩擦力贡献,第二项是由土的黏聚力和土水相互作用贡献。

当 $ζ = 1$ ,极限应力状态即为Fredlund强度理论,此时安全系数为

$F = \frac{τ_{f}}{τ} = \frac{\tan φ^{'}}{\tan β} + \frac{c^{'}}{γ D \sin β} + \frac{S_{r} (u_{a} - u_{w}) \tan φ^{'}}{γ D \sin β}$ 。

(16)

对比式（15）和（16）可知,C-F准则和Fredlund准则求得的安全系数差别,是由于方程（15）中因式[B(1-sinδ)/cos $δ +$ Ctan $δ$ ],使土有效黏聚力和土水相互作用对安全系数的贡献减小。

当无限边坡滑动面处于地下水位线以下的饱和状态时S_r= 1,该式可退化为饱和土无限边坡安全系数表达式^[28]：

$F = \frac{τ_{f}}{τ} = \frac{\tan φ^{'}}{\tan β} + \frac{c^{'}}{γ D \sin β} - \frac{u_{w} \tan φ^{'}}{γ D \sin β}$ 。

(17)

不难看出,无限边坡的安全系数随着厚度的增加而减小,无限边坡存在临界厚度：

$D^{*} = \frac{c \cos φ^{'}}{γ \sin (β - φ^{'})}$ 。

(18)

因此无限边坡模型只能分析临界厚度以内坡体的强度较上层坡体强度大的边坡。本文假设临界厚度以下的边坡为基岩,潜在滑动面位于临界厚度以上。

2.2 稳定渗流作用下无限边坡稳定性

无渗流时,地下水位线以上基质吸力的分布：

$u_{a} - u_{w} = γ_{w} (D_{w} - D) / \cos θ$ 。

(19)

Lu等^[29]根据非饱和土达西定理,假定渗透系数函数为Gardner模型,推导出稳定渗流作用下基质吸力的分布：

$u_{a} - u_{w} = \frac{- 1}{α} \ln [(1 + q / k_{s}) e^{\frac{- α γ_{w} (D_{w} - D)}{\cos β}} - q / k_{s}]$ ,

(20)

式中,q/k_s >-1,为无量纲量,当|q|>k_s时,多余的水流量无法入渗,在地表形成径流,q为渗流量,k_s为饱和土渗透系数,表示土体单位时间的最大入渗量。q/k_s表示非饱和土中最小的水力坡降,在稳定渗流作用下,q/k_s的大小能反映渗流的强弱。当q/k_s趋向-1时,非饱和土接近饱和状态。因此在下文进行渗流影响下的无限边坡稳定性分析时,取q/k_s为0,-0.5和-0.99,分别表示无渗流、非饱和渗流和近饱和渗流。

坡体中土的有效饱和度可根据土水特征曲线模型Van Genuchten模型得出

$S_{r} = {\frac{1}{1 + {[α (u_{a} - u_{w})]}^{n}}}^{1 - 1 / n}$ ,

(21)

式中,α和n为经验拟合参数,与孔径大小有关,α和n的取值范围^[30]为1.1<n<8.5,0<α<0.5 kPa^-1。

由式（20）和（21）可得稳定渗流作用下的M：

$M = \frac{- 1}{α} \frac{\ln [(1 + q / k_{s}) e^{- α γ_{w} (D_{w} - D) / \cos β} - q / k_{s}]}{{1 + {- \ln [(1 + q / k_{s}) e^{- α γ_{w} (D_{w} - D) / \cos β} - q / k_{s}]}^{n}}^{1 - 1 / n}} 。$

(22)

因此渗流作用下,采用C-F模型计算非饱和土无限边坡安全系数为

$\begin{array}{l} F = \frac{τ_{f}}{τ} = \frac{\tan δ}{\tan β} + (\frac{c^{'}}{γ D \sin β} + \frac{M \tan φ^{'}}{γ D \sin β}) \cdot \\ [B \frac{(1 - \sin δ)}{\cos δ} + C \tan δ] (φ^{'} \leq δ < 90 °) \end{array}$ 。

(23)

式（23）可变形为

$\begin{array}{l} F = B (\frac{c^{'} + M \tan φ^{'}}{γ D \sin β}) \frac{(1 - \sin δ)}{\cos δ} + \\ [\frac{1}{\tan β} + C (\frac{c^{'} + M \tan φ^{'}}{γ D \sin β})] \tan δ (φ^{'} \leq δ < 90 °) \end{array}$ 。

(24)

在边坡稳定性分析中,考虑最不稳定的因素,因此对F的最小取值进行分析。

$\begin{matrix} δ = \arcsin [\frac{\frac{c^{'} + M \tan φ^{'}}{γ D \sin β} B - (\frac{c^{'} + M \tan φ^{'}}{γ D \sin β} C + \frac{1}{\tan β})}{\frac{c^{'} + M \tan φ^{'}}{γ D \sin β} B}] \\ (φ^{'} \leq δ < 90 °) \end{matrix}$ 。

(25)

当δ满足式（25）时,F取最小值。

δ的变化说明极限应力状态位于图1强度包络线QP部分,土体的破坏状态由抗拉强度决定,不同深度处安全系数取最小值的应力状态所在平面的方向与大小主应力的方向的夹角是变化的,且可能不平行于潜在滑动面,因此在边坡失稳过程中,不符合相关联流动法则,且土体不仅发生摩擦剪切滑移,还会有断裂和破碎。因此,定义δ为破裂角更符合边坡失稳中滑带形成的实质。

当滑动面位于地下水位线以下,为饱和土边坡时：

$\begin{matrix} F = B (\frac{c^{'}}{γ D \sin β}) \frac{(1 - \sin δ)}{\cos δ} + [\frac{1}{\tan β} - \frac{γ_{w} D_{w}}{γ D \sin β} + \\ C (\frac{c^{'}}{γ D \sin β})] (φ^{'} \tan δ \leq δ < 90 °) \end{matrix}$ ,

(26)

此时：

$\begin{matrix} δ = \arcsin [\frac{\frac{c^{'}}{γ D \sin β} B - (\frac{c^{'}}{γ D \sin β} C + \frac{1}{\tan β} - \frac{γ_{w} D_{w}}{γ D \sin β})}{\frac{c^{'}}{γ D \sin β} B}] \\ (φ^{'} \leq δ < 90 °) \end{matrix}$ 。

(27)

F取最小值,在不考虑饱和土顺坡向渗流时,该式与Michalowski采用运动学方法（上限理论）所得安全系数一致^[8]。

3. 参数和结果分析

本文选用3种典型土土坡对计算结果进行分析,表1给出了3种土的物理力学参数,参数的取值参考文献[31]。

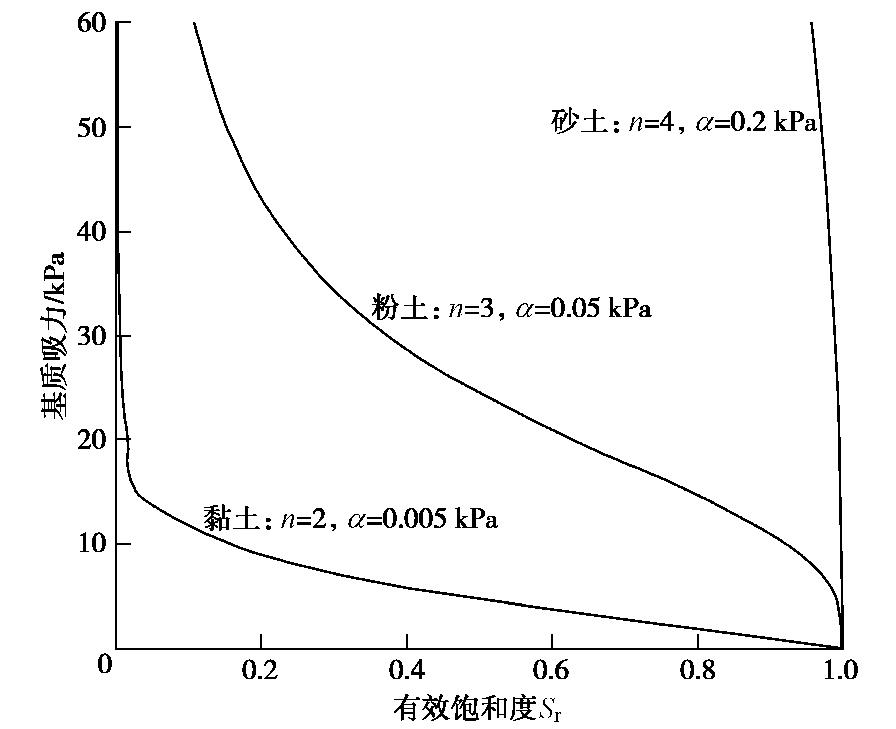
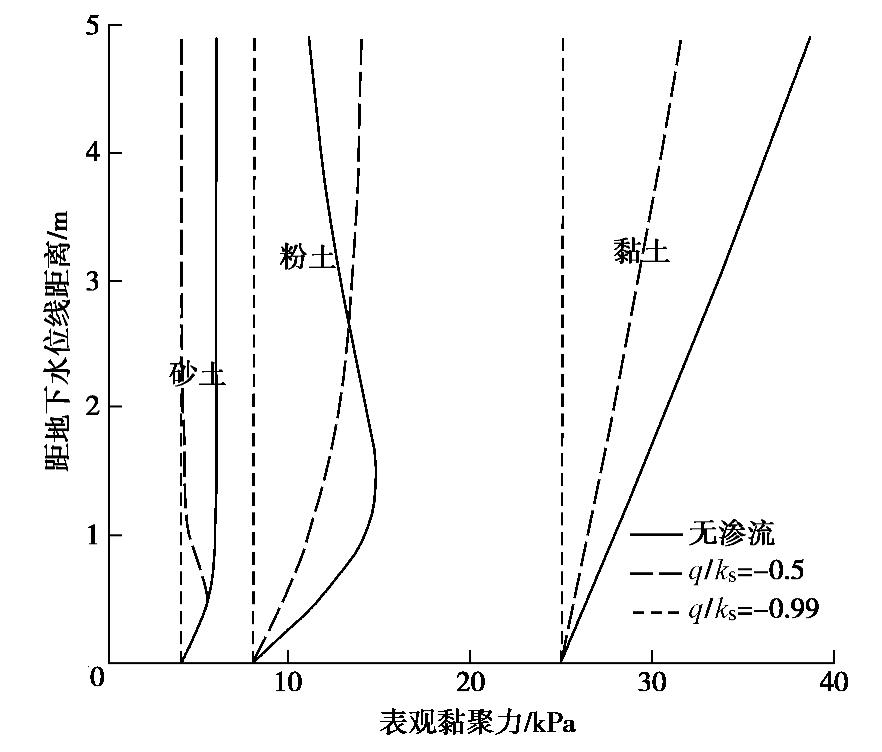
表 1 土的物理力学参数

Table 1. mechanical and hydrologic parameters of soils

土类	n	α	c′	ϕ′
砂土	4	0.2	4	33
粉土	3	0.05	8	28
黏性土	2	0.005	25	12

下载: 导出CSV

| 显示表格

3种土的土水特征曲线如图4所示。根据公式（10）和（22）可以得出表观黏聚力的分布,图5给出了q/k_s分别为0,-0.5,-0.99等不同稳定渗流条件下的有效黏聚力的分布。在不同的渗流条件下,砂土的有效黏聚力变化最小,最大为2 kPa,黏土的最大,可达13 kPa,当q/k_s=-0.99时,土体接近饱和状态,表观黏聚力等于有效黏聚力。在砂土和粉土中,不同渗流条件时,饱和度和基质吸力分布的变化,使渗流引起的黏聚力的变化不单一,如q/k_s=-0.5的渗流时,表观黏聚力在近地表大于无渗流时的黏聚力。因此非饱和土边坡的稳定性分析较饱和土复杂。

图 4 土水特征曲线

Figure 4. Soil-water characteristic curves for sand, silt and clay

下载: 全尺寸图片幻灯片

图 5 表观黏聚力分布

Figure 5. Apparent cohesion profiles under various steady seepages

下载: 全尺寸图片幻灯片

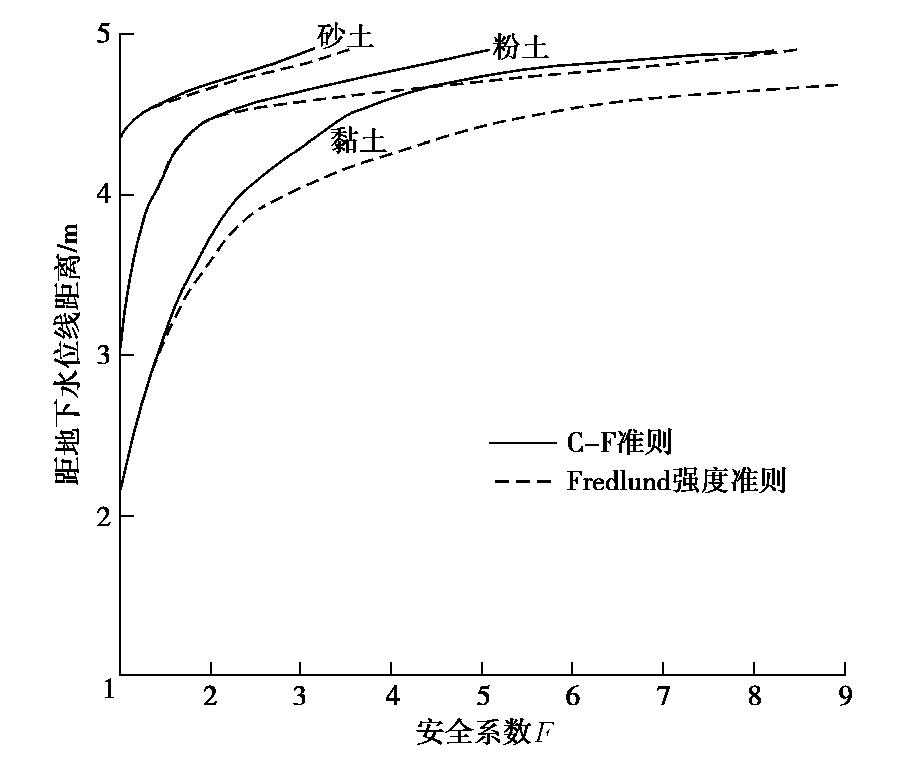
安全系数的最小值可由式（24）和（25）得到,如图6为坡角β=45°,无渗流时,3种土坡的计算结果。

图 6 3种土安全系数分布

Figure 6. Safety factor profiles of C-F criterion and Fredlund strength criterion for sand, silt and clay

下载: 全尺寸图片幻灯片

（1）在近地表0～1 m的浅层滑坡中,C-F准则（ζ=0）与Fredlund准则所得的安全系数相差较大,C-F准则计算的安全系数明显降低；在距地表较深的位置,两种准则所得安全系数的差别不明显。这是因为距地表较深的坡体中（D比较大）,在静态或准静态,坡体中自重应力较大,由自重引起的地应力比较大,且为压应力,应力状态处于强度准则中距离原点较远的压应力区,坡体的破坏受压剪屈服准则的控制,安全系数在ϕ′ =δ时取最小值,与拉剪强度包络线的形状无关,因此C-F准则与Fredlund准则所得安全系数几乎无差别；而在距地表较浅的位置,坡体中的应力较小,其破坏可能受拉剪屈服准则的影响,安全系数在ϕ′ <δ时取最小值,因此拉剪区强度准则的不同,对安全系数的计算结果影响较大。但在膨胀土边坡中,土体在干化过程中,会产生收缩的拉应力,使坡体中的应力减小,因此C-F准则在膨胀土边坡中会表现出更大的作用。

（2）C-F准则较Fredlund准则计算的安全系数,黏性土降低最大,对砂土和粉土的影响较小,即表观黏聚力越大,边坡稳定性评价结果受抗拉强度准则的影响越大。

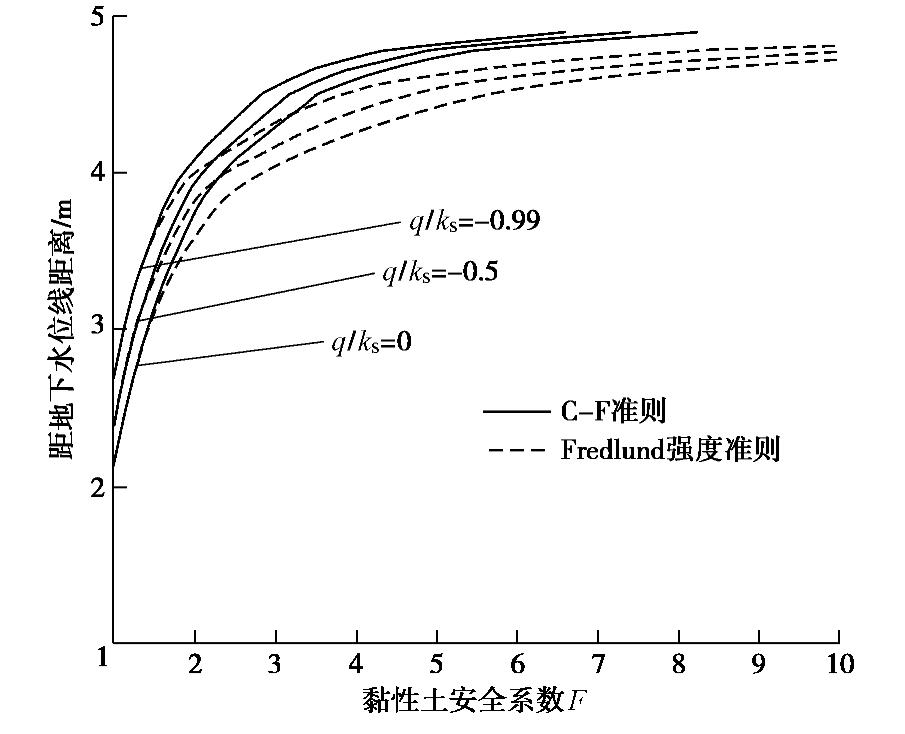
选择黏性土为研究对象,不同渗流条件下坡体的安全系数如图7所示。随着入渗强度的增加,不同深度处潜在滑动面的安全系数均在减小,采用C-F准则的安全系数降幅较小。当q/k_s=-0.99时,所得土坡的安全系数最小,此时土体接近饱和状态,所计算的安全系数可近似等于采用饱和土强度理论的安全系数；当q/k_s=0时,考虑非饱和特性的安全系数较饱和状态提高了25%（C-F准则）,50%（Fredlund准则）,非饱和土强度对地下水位较深的干旱地区边坡稳定性有重要影响,但降雨入渗作用可使非饱和土强度大大降低,因此在施工过程中,应避开雨季。

图 7 不同渗流的安全系数分布

Figure 7. Safety factor profiles of clay slope for C-F criterion and Fredlund strength criterion with various steady seepage conditions

下载: 全尺寸图片幻灯片

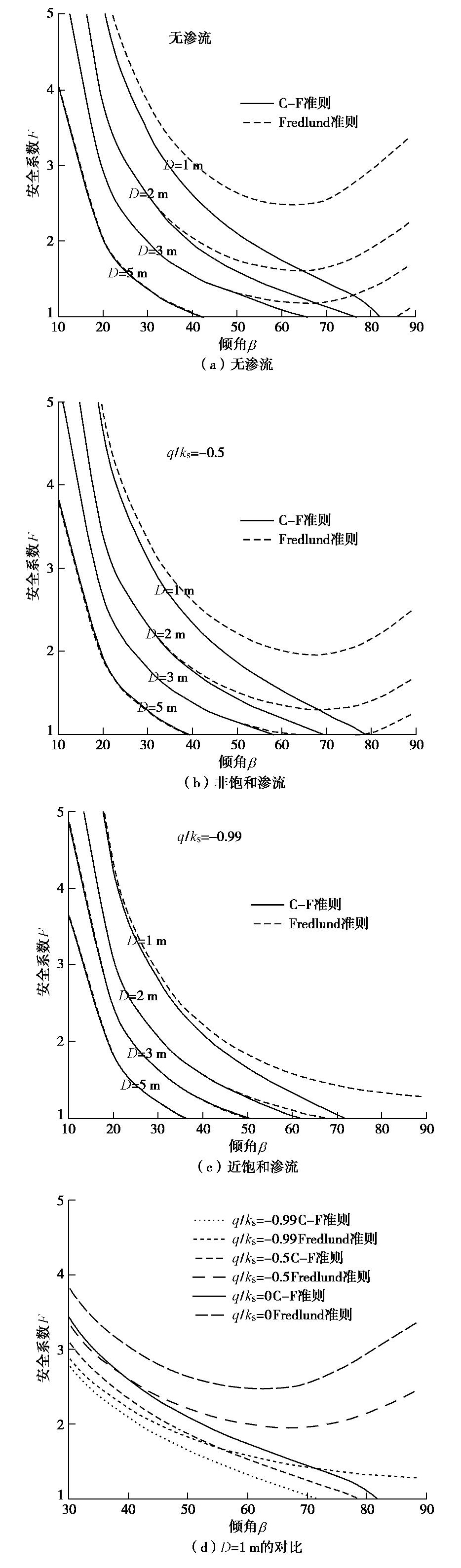
坡角是无限边坡的重要影响参数,图8为潜在滑动面的厚度D从1 m到5 m时,不同坡角的黏性土无限边坡在不同入渗条件下的安全系数。

图 8 坡角的影响

Figure 8. Safety factors for C-F criterion and Fredlund strength criterion under different slope angles

下载: 全尺寸图片幻灯片

（1）不同坡度,不同降雨条件的C-F准则均导致安全系数降低。

（2）坡度越大（坡度大于60°）、深度越浅,安全系数的降低越明显。

（3）渗流越强,安全系数越小,C-F准则导致安全系数的降低越小（从无渗流状态的62%到接近饱和状态的37%）。因此在非饱和土中,抗拉强度对边坡稳定性分析的影响较大,这是因为在非饱和土,土水作用对抗拉强度的作用比较明显,非饱和土抗拉强度的研究较饱和土有更重要的意义。

值得注意的是：在无渗流作用下,Fredlund准则（式（24）,ζ=1）计算的安全系数,随着坡角的增大,并非单调减小,安全系数在某个坡度出现最小值。在土坡分析中,通常认为随着倾角的增加,安全系数应该减小,但本文采用考虑土体非饱和特性的Fredlund准则进行边坡稳定性分析时,在坡度较大的情况下（ $β >$ 70°）出现了相反的结果,这是因为在高陡边坡的浅层,坡体的应力较小,破坏受拉剪包络线控制,Fredlund准则明显高估了非饱和土的抗拉强度。因此本文提出的C-F准则得出的安全系数更为合理,在高陡边坡稳定性分析时,坡体材料的抗拉强度有着至关重要的影响,不可简单地应用外推法得到。

4. 结论

由于非饱和土抗拉强度的不确定性,且Fredlund准则明显高估了非饱和土抗拉强度,本文提出了基于Fredlund准则的考虑抗拉强度部分剪断的C-F准则,考虑抗拉强度的不同处理方式,对无限边坡稳定性的影响。对比分析C-F准则和Fredlund准则对3类土不同渗流作用的无限边坡安全系数的影响。结论如下：

（1）在近地表0～1 m的浅层滑坡中,C-F准则导致无限边坡安全系数的降低,且黏聚力越大,安全系数的降低越多。因此,抗拉强度准则对黏聚力较大的浅层边坡稳定性评价中有重要影响。

（2）考虑坡体非饱和特性的安全系数较饱和状态有所提高,渗流作用降低土坡安全系数,C-F准则相比Fredlund准则的降低作用小。

（3）对于高陡边坡,C-F准则导致无限边坡安全系数的降低更加明显,Fredlund准则由于高估非饱和土的抗拉强度不再适合进行高陡边坡的稳定性分析,C-F准则的分析结果更为合理。

图 1 平面应变C-F准则

Figure 1. Strength envelope of C-F criterion

下载: 全尺寸图片幻灯片

图 2 C-F准则截面（吸力恒定）

Figure 2. Cross section of C-F criterion (constant matrix suction)

下载: 全尺寸图片幻灯片

图 3 无限斜坡模型示意图

Figure 3. Schematic diagram for shallow infinite slope model

下载: 全尺寸图片幻灯片

图 4 土水特征曲线

Figure 4. Soil-water characteristic curves for sand, silt and clay

下载: 全尺寸图片幻灯片

图 5 表观黏聚力分布

Figure 5. Apparent cohesion profiles under various steady seepages

下载: 全尺寸图片幻灯片

图 6 3种土安全系数分布

Figure 6. Safety factor profiles of C-F criterion and Fredlund strength criterion for sand, silt and clay

下载: 全尺寸图片幻灯片

图 7 不同渗流的安全系数分布

Figure 7. Safety factor profiles of clay slope for C-F criterion and Fredlund strength criterion with various steady seepage conditions

下载: 全尺寸图片幻灯片

图 8 坡角的影响

Figure 8. Safety factors for C-F criterion and Fredlund strength criterion under different slope angles

下载: 全尺寸图片幻灯片

表 1 土的物理力学参数

Table 1 mechanical and hydrologic parameters of soils

土类 n α c′ ϕ′

砂土 4 0.2 4 33
粉土 3 0.05 8 28
黏性土 2 0.005 25 12

下载: 导出CSV

参考文献(31)

[1]	杨明成, 郑颖人. 基于极限平衡理论的局部最小安全系数法[J]. 岩土工程学报, 2002, 24(5): 600-604. doi: 10.3321/j.issn:1000-4548.2002.05.013 YANG Ming-cheng, ZHENG Ying-ren. Local minimum factor-of- safety method based on limit equilibrium theory[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 600-604. (in Chinese) doi: 10.3321/j.issn:1000-4548.2002.05.013
[2]	谭晓慧, 王建国, 刘新荣, 等. 边坡稳定的有限元可靠度计算及敏感性分析[J]. 岩石力学与工程学报, 2007, 26(1): 115-122. doi: 10.3321/j.issn:1000-6915.2007.01.016 TAN Xiao-hui, WANG Jian-guo, LIU Xin-rong. et al. Finite element reliability computation and sensitivity analysis of slope stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 115-122. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.01.016
[3]	刘才华, 陈从新, 冯夏庭. 库水位上升诱发边坡失稳机理研究[J]. 岩土力学, 2005, 26(5): 769-773. doi: 10.3969/j.issn.1000-7598.2005.05.018 LIU Cai-hua, CHEN Cong-xin, FENG Xia-ting. Study on mechanism of slope instability due to reservoir water level rise[J]. Rock and Soil Mechanics, 2005, 26(5): 769-773. (in Chinese) doi: 10.3969/j.issn.1000-7598.2005.05.018
[4]	陈善雄, 陈守义. 考虑降雨的非饱和土边坡稳定性分析方法[J]. 岩土力学, 2001, 22(4): 447-450. doi: 10.3969/j.issn.1000-7598.2001.04.019 CHEN Shan-xiong, CHEN Shou-yi. Analysis of stability of unsaturated soil slope due to permeation of rainwater[J]. Rock and Soil Mechanics, 2001, 22(4): 447-450. (in Chinese) doi: 10.3969/j.issn.1000-7598.2001.04.019
[5]	徐晗, 朱以文, 蔡元奇, 等. 降雨入渗条件下非饱和土边坡稳定分析[J]. 岩土力学, 2005, 26(12): 1957-1962. doi: 10.3969/j.issn.1000-7598.2005.12.019 XU Han, ZHU Yi-wen, CAI Yuan-qi, et al. Stability analysis of unsaturated soil slopes under rainfall infiltration[J]. Rock and Soil Mechanics, 2005, 26(12): 1957-1962. (in Chinese) doi: 10.3969/j.issn.1000-7598.2005.12.019
[6]	李荣建, 于玉贞, 邓丽军, 等. 非饱和土边坡稳定分析方法探讨[J]. 岩土力学, 2007, 28(10): 2060-2064. doi: 10.3969/j.issn.1000-7598.2007.10.010 LI Rong-jian, YU Yu-zhen, DENG Li-jun, et al. Discussion on stability analysis of unsaturated soil slopes[J]. Rock and Soil Mechanics, 2007, 28(10): 2060-2064. (in Chinese) doi: 10.3969/j.issn.1000-7598.2007.10.010
[7]	LU N, GODT J. Infinite slope stability under steady unsaturated seepage conditions[J]. Water Resources Research, 2008, 44(11): W11404.
[8]	MICHALOWSKI R L. Failure potential of infinite slopes in bonded soils with tensile strength cut-off.[J]. Canadian Geotechnical Journal, 2018, 55(4): 477-485. doi: 10.1139/cgj-2017-0041
[9]	马崇武, 刘忠玉. 降雨入渗时无限边坡的水平位移与稳定性分析[J]. 岩土力学, 2007, 28(增刊1): 563-568. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2007S1114.htm MA Hong-wu, LIU Zhong-yu. Horizontal displacements and stability analysis of infinite slopes under rainfall infiltration[J]. Rock and Soil Mechanics, 2007, 28(S1): 563-568. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2007S1114.htm
[10]	王俊, 黄润秋, 聂闻, 等. 基于无限边坡算法的降雨型滑坡预警系统的模型试验研究[J]. 岩土力学, 2014, 35(12): 3503-3510. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412022.htm WANG Jun, HUANG Run-qiu, NIE Wen. Experimental study of early warning system model of landslide induced by rainfall based on infinite slope method[J]. Rock and Soil Mechanics, 2014, 35(12): 3503-3510. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412022.htm
[11]	唐小松, 李典庆, 周创兵, 等. 不完备概率信息条件下边坡可靠度分析方法[J]. 岩土工程学报, 2013, 35(6): 1027-1034. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201306007.htm TANG Xiao-song, LI Dian-qing, ZHOU Chuang-bing. Modeling dependence between shear strength parameters using copulas and its effect on slope reliability[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1027-1034. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201306007.htm
[12]	YIN P, VANAPALLI S K. Model for predicting the tensile strength of unsaturated cohesionless soils[J]. Canadian Geotechnical Journal, 2018, 55(9): 1313-1333. doi: 10.1139/cgj-2017-0376
[13]	ABD A H, UTILI S. Design of geosynthetic-reinforced slopes in cohesive backfills[J]. Geotextiles and Geomembranes, 2017, 45(6): 627-641. doi: 10.1016/j.geotexmem.2017.08.004
[14]	MICHALOWS K L. Stability assessment of slopes with cracks using limit analysis[J]. Canadian Geotechnical Journal, 2013, 50(10): 1011-1021. doi: 10.1139/cgj-2012-0448
[15]	汤连生, 赵占仑, 钟明灯, 等. 滑坡裂隙与边坡拉剪耦合破坏的模型试验研究[C]//裂隙性黏土的工程特性及应用专题学术研讨会. 2018, 武汉: 111-117. TANG Lian-sheng, ZHAO Zhan-lun, ZHONG Ming-deng, et al. Model experimental study on cracks and tensile-shear coupling failure of landslide[C]//Seminar on Engineering Properties and Applications of Fissure Clay, 2018, Wuhan, 111-117. (in Chinese)
[16]	LU N, WU B, TAN C P. Tensile strength characteristics of unsaturated sands[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2007, 133(2): 144-154.
[17]	朱崇辉, 刘俊民, 严宝文, 等. 非饱和黏性土的抗拉强度与抗剪强度关系试验研究[J]. 岩石力学与工程学报, 2008, 27(增刊2): 3453-3453. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2008S2026.htm ZHU Chong-hui, LIU Jun-min, YAN Bao-wen, et al. Experimental study on the relationship between tensile strength and shear strength of unsaturation clay earth material[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S2): 3453-3453. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2008S2026.htm
[18]	孔小昂, 蔡国庆, 刘真真, 等. 非饱和黏土的张拉-剪切耦合强度研究[J]. 岩土力学, 2017, 38(增刊2): 9-17. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2017S2002.htm KONG Xiao-ang, CAI Guo-qing, LIU Zhen-zhen, et al. Research on tensile-shear coupling strength of unsaturated clays[J]. Rock and Soil Mechanics, 2017, 38(S2): 9-17. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2017S2002.htm
[19]	李荣建, 刘军定, 郑文, 等. 基于结构性黄土抗拉和抗剪特性的双线性强度及其应用[J]. 岩土工程学报, 2013, 35(S2): 247-252. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2042.htm LI Ring-jian, LIU Jun-ding, ZHENG Wen, et al. A bilinear strength formula for structured loess based on tensile strength and shear strength and its application[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 247-252. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2042.htm
[20]	FREDLUND D G, MORGENSTERN N R, WIDGER R A. The shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 1978, 15(3): 313-321.
[21]	陈敬虞, FREDLUNDDG . 非饱和土抗剪强度理论的研究进展[J]. 岩土力学, 2003, 24(增刊2): 655-660. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201802002.htm CHEN Jing-yu, FREDLUND D G. Advance in research on shear strength of unsaturated soils[J]. Rock and Soil Mechanics, 2003, 24(S2): 655-660. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201802002.htm
[22]	汤连生. 从粒间吸力特性再认识非饱和土抗剪强度理论[J]. 岩土工程学报, 2001, 23(4): 412-417. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200104006.htm TANG Lian-sheng. New suggestion on shear strength in unsaturated soil based on suction between grains[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 412-417. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200104006.htm
[23]	PAUL B. A modification of the Coulomb-Mohr theory of fracture[J]. Journal of Applied Mechanics, 1961, 28(2): 259-268.
[24]	REYNOLDS O. On the dilatancy of media composed of rigid particles in contact: with experimental illustrations[J]. Philosophical Magazine, 1885, 20(127): 469-482
[25]	PARK D, MICHALOWS K L. A cone surface in three- dimensional analyses of slopes with tension cut-off[J]. Geotechnical Research, 2018, 5(2): 51-67.
[26]	MAYNE P W. Stress anisotropy effects on clay strength[J]. Journal of Geotechnical Engineering, 1985, 111: 356-366.
[27]	赵成刚, 蔡国庆. 非饱和土广义有效应力原理[J]. 岩土力学, 2016, 30(11): 3232-3236. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200911004.htm ZHAO Cheng-gang, CAI Guo-qing. Principle of generalized effective stress for unsaturated soils[J]. Rock and Soil Mechanics, 2016, 30(11): 3232-3236. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200911004.htm
[28]	DUNCAN J M, WRIGHT S G. Soil Strength and Slope Stability[M]. New Jersey: John Wiley & Sons, Inc, 2005.
[29]	LU N, GRIFFITHS D V. Suction stress profiles in unsaturated soils[J]. J Geotech Geoenviron Eng, 2004, 130(10): 1063-1076.
[30]	GENUCHTEN M T V. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils1[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898.
[31]	LUN , LIKOSW . 非饱和土力学[M]. 北京: 高等教育出版社, 2012. LU N, LIKOS W. Soil Mechanics for Unsaturated Soils[M]. Beijing: Higher Education Press, 2012. (in Chinese)

施引文献(13)

期刊类型引用(6)

1.	张德沧，毛佳，戴妙林，邵琳玉，赵兰浩. 圆化离散单元法的改进及其在岩体断裂过程中的应用. 岩土工程学报. 2024(09): 1974-1983 . 本站查看
2.	何荣兴，张智源，张星宇，章雅雯. 诱导下岩体裂隙扩展规律研究存在问题及对策. 中国矿业. 2024(10): 168-176 . 百度学术
3.	刘洋，吴志军，储昭飞，翁磊，徐翔宇，周原，高波，毛春光. 基于FDEM的围压条件下机械冲击破岩机理研究. 中南大学学报(自然科学版). 2023(03): 866-879 . 百度学术
4.	杨奎斌，朱彦鹏. 考虑后缘裂缝影响的均质土坡滑动面形式及搜索研究. 应用基础与工程科学学报. 2022(05): 1216-1227 . 百度学术
5.	张亚军，莫思阳，张友良. 基于修正牛顿-拉普森迭代的数值流形法. 计算机仿真. 2022(09): 394-397+440 . 百度学术
6.	韩笑. 基于高阶块体元-有限元建模的混凝土细观数值分析. 粉煤灰综合利用. 2021(03): 56-63 . 百度学术

其他类型引用(7)

资源附件(0)

图(8) / 表(1)

计量

文章访问数: 337
HTML全文浏览量: 49
PDF下载量: 272
被引次数: 13

0. 引言
1. 抗拉强度部分剪断准则
2. 无限边坡稳定性
2.1 非饱和土无限边坡稳定性
2.2 稳定渗流作用下无限边坡稳定性
3. 参数和结果分析
4. 结论

考虑抗拉强度剪断的非饱和土无限边坡稳定性分析 English Version

作者简介: 李梦姿(1992—),女,博士研究生,主要从事非饱和土力学相关研究工作。E-mail: mzli118@163.com

通讯作者: 蔡国庆, E-mail: guoqing.cai@bjtu.edu.cn

计量

出版历程