盆地内外介质阻抗比对盆地地表地震动及次生Rayleigh面波的影响

于彦彦; 丁海平; 刘启方

doi:10.11779/CJGE202004009

盆地内外介质阻抗比对盆地地表地震动及次生Rayleigh面波的影响 English Version

苏州科技大学江苏省结构工程重点实验室,江苏　苏州　215011

基金项目:

国家自然科学基金青年基金项目 51808371

江苏省高等学校自然科学研究面上项目 18KJB560017

详细信息

作者简介:
于彦彦(1985—),男,博士,讲师,主要从事场地地震效应及波动数值模拟研究。E-mail: yyy_usts@126.com

中图分类号: TU447
计量
- 文章访问数: 226
- HTML全文浏览量: 25
- PDF下载量: 80
出版历程
- 收稿日期: 2019-07-30
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-03-31

Effects of impedance ratio between basin sediment and surrounding rock on seismic ground motions and basin-induced Rayleigh waves

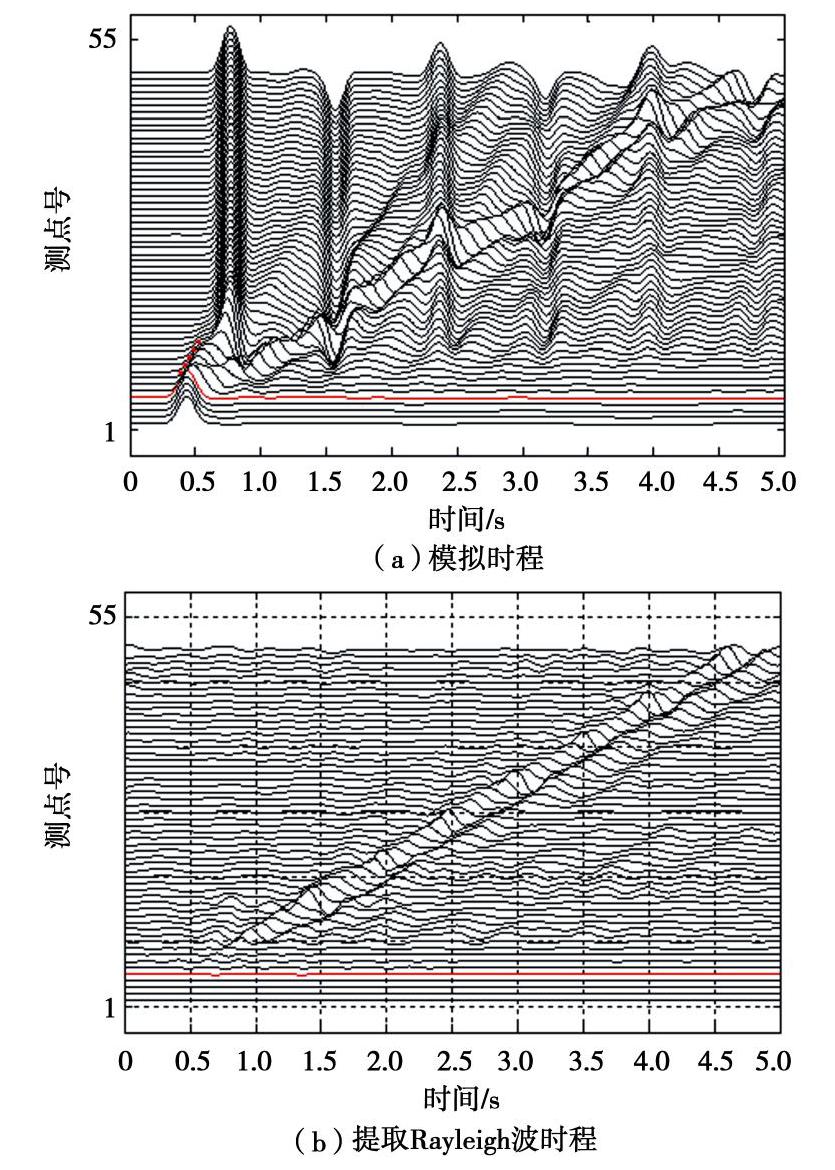
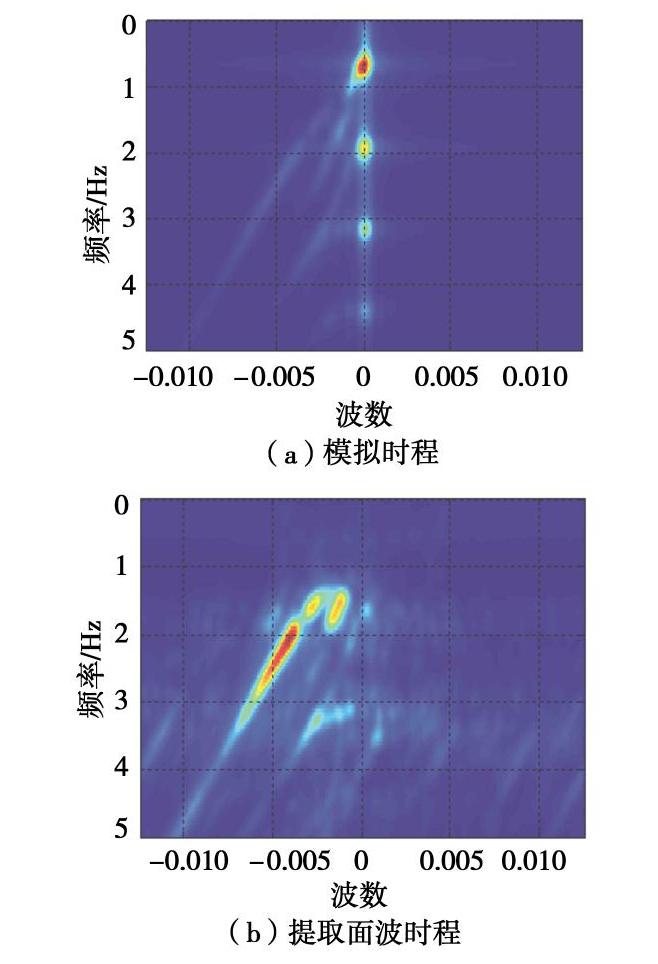
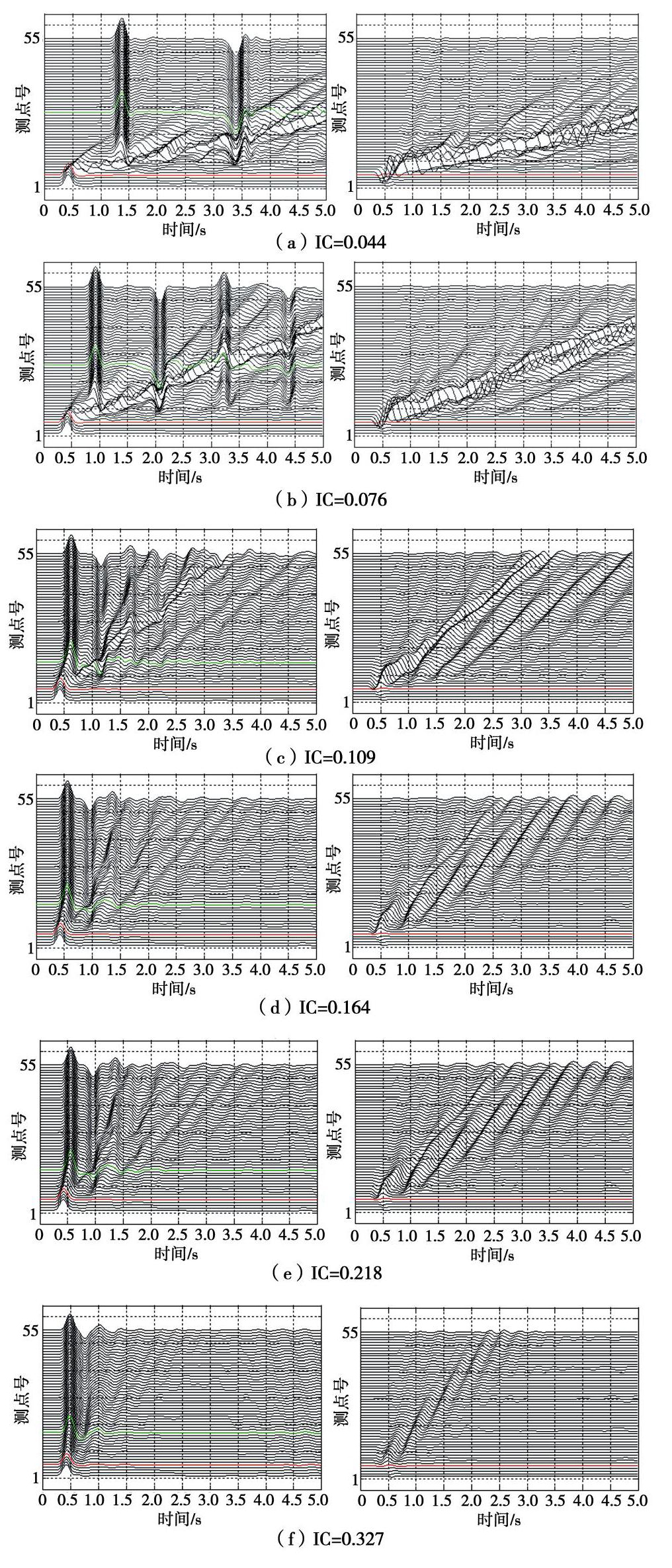
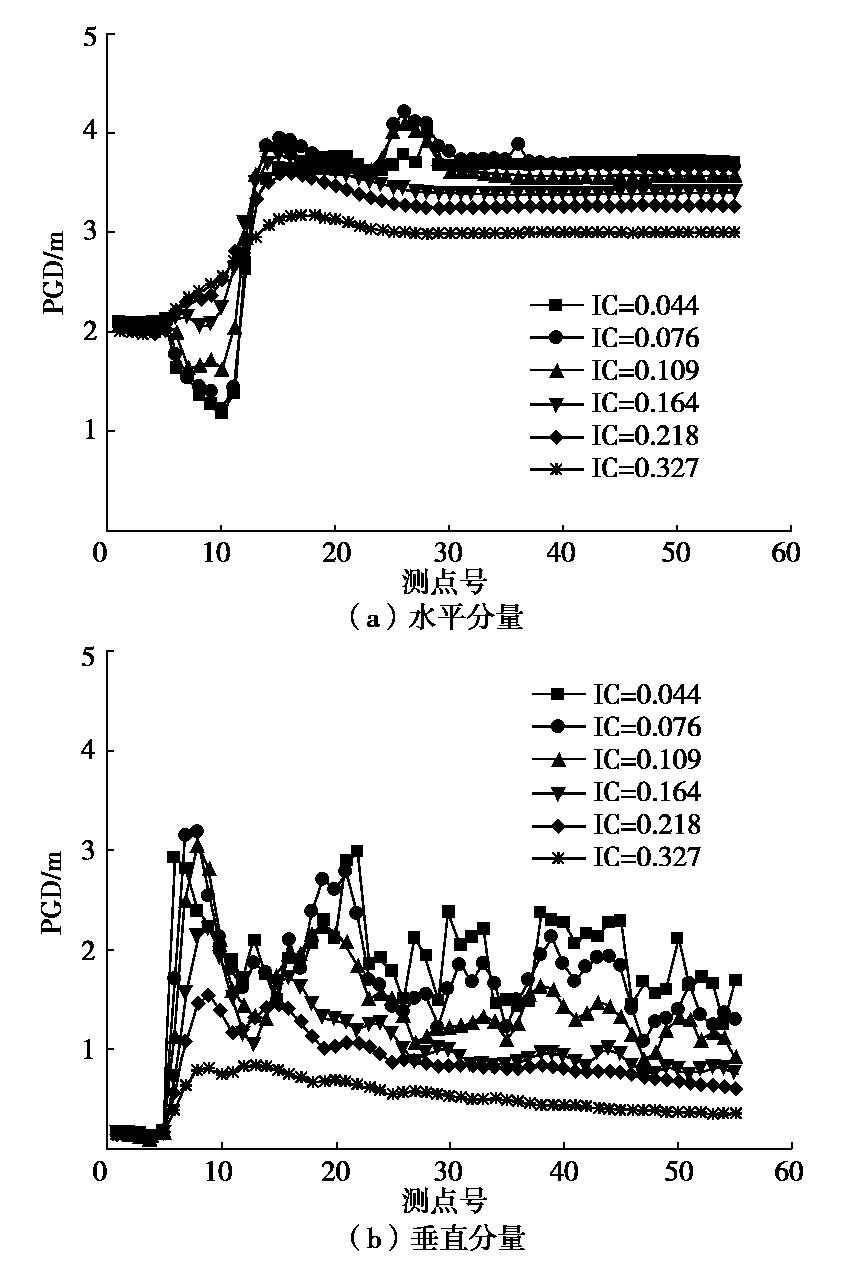
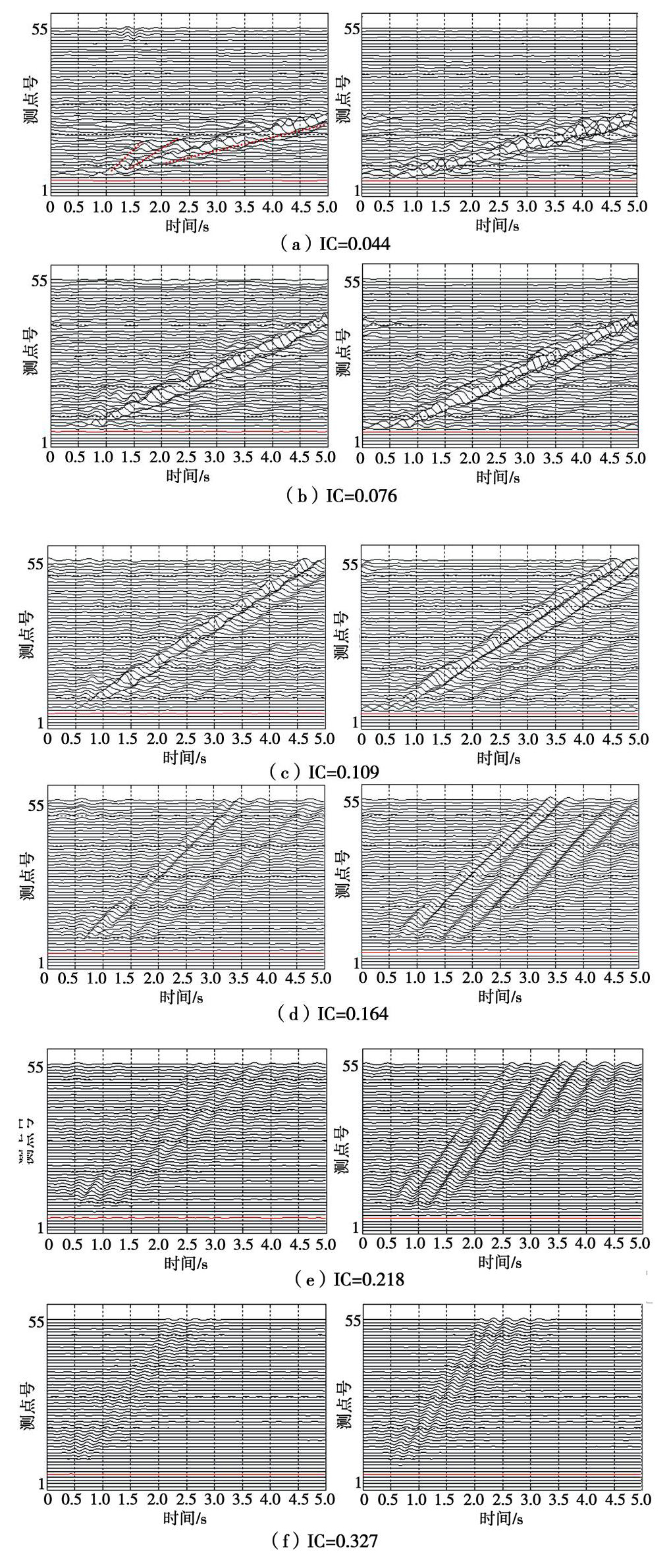
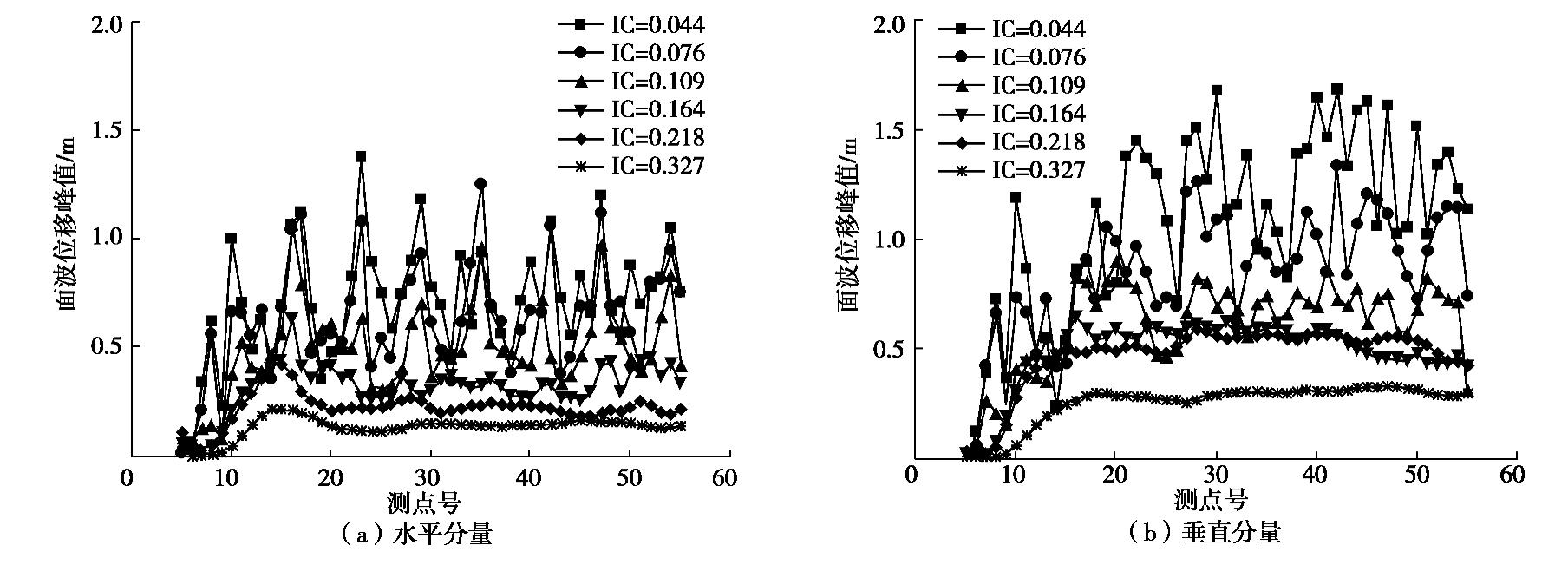
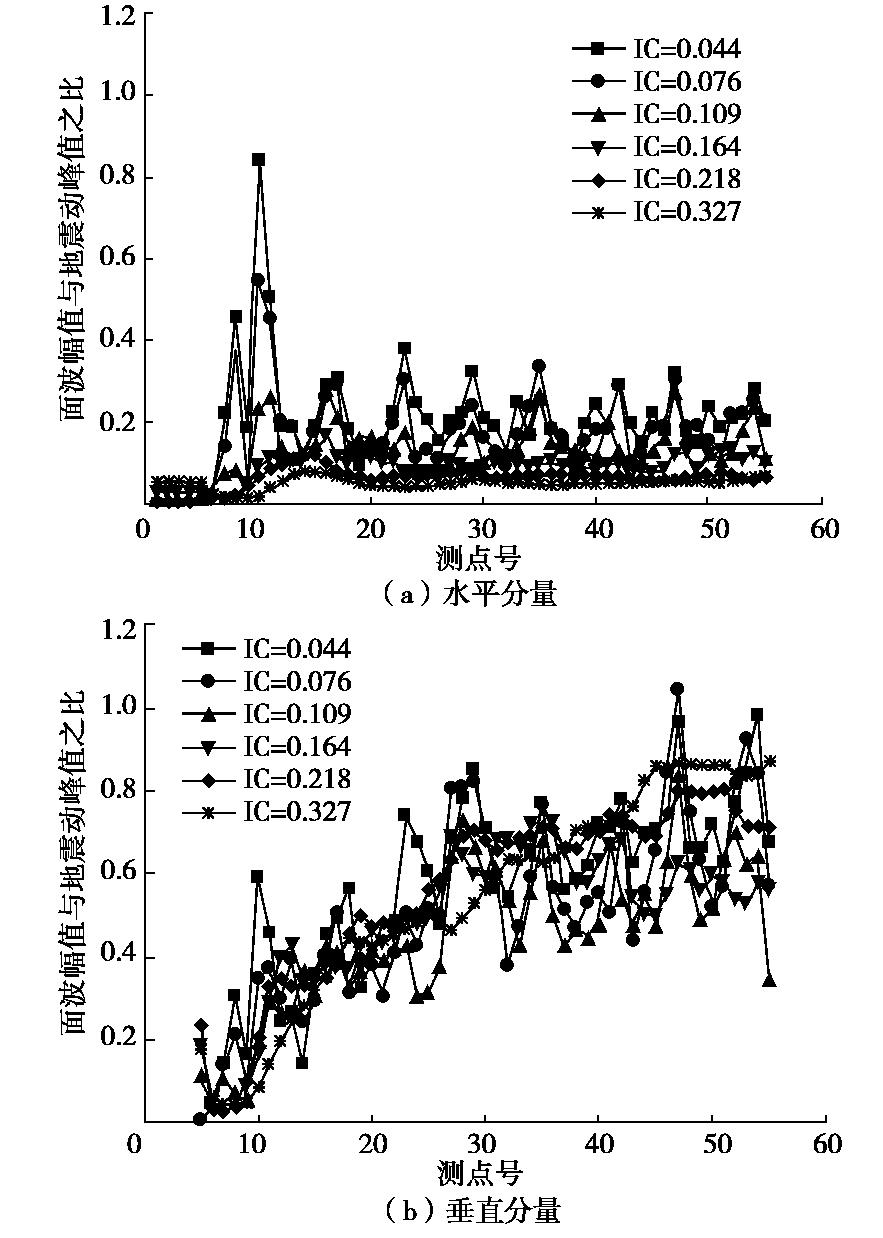
Key Laboratory of Structure Engineering of Jiangsu Province, Suzhou University of Science and Technology, Suzhou 215011, China

摘要

摘要: 采用综合f-k滤波和基于S变换的极化分析方法,从盆地观测点的模拟时程中提取Rayleigh面波,研究盆地内外介质的阻抗比（IC）对盆地地表地震动及次生面波的影响。结果表明：①此方法能较好地识别和提取Rayleigh面波震相。②盆地放大效应受IR影响显著。水平分量最大放大系数（AF_max）随IC的增加而增大,最大约1.15；垂直分量AF_max随之降低,最大值0.85左右。同时,盆地斜边区域水平分量地震动的削减作用随IC减小而增强。③IC对盆地显著放大区域的分布特征影响明显。IC较小时,盆地内存在多个显著放大区域；IC较大时,此区域仅出现在盆地边缘。④随IC增加,两分量的面波幅值降低,面波持时变长,传播速度增大。⑤IC较小时,面波幅值在盆地内振荡明显,随IC增大,该值在盆地边缘处最大,向内部基本不变。⑥面波幅值与地震动峰值之比在水平分量上随IC增大而降低,最大比值出现在盆地边缘；在垂直分量上受IC影响不明显,主要随与盆地边缘距离的增加而增大。
- 盆地 /
- Rayleigh面波识别 /
- 阻抗比 /
- 地震动 /
- 放大效应
Abstract: A method for extracting Rayleigh wave phases from simulated seismograms is proposed by incorporating the F-K filtering and polarization analysis based on the time-frequency S transform. Then the effects of impedance ratio (IC) between basin sediment and surrounding rock on the basin ground motion and basin-induced surface wave are investigated. The results show that: (1) The Rayleigh waves can be satisfactorily identified and extracted by using this method. (2) The amplification effects of the basin are significantly affected by IC. The maximum amplification factor (AF_max) of the horizontal component increases with growing IC, with a largest value of about 1.15 for the studied cases. Contrastly, AF_max of the vertical component decreases with larger IC with the largest value of 0.85. In addition, horizontal ground motion at basin slope region is gradually weakened with reduced IC. (3) IC has obvious influences on the distribution features of intensely amplified regions of the basin. Under small IC, a few such regions occur in the basin, however, under large IC, these regions only appear at the basin edge. (4) With increasing IC, the amplitude of the basin-induced Rayleigh waves becomes lower, but the duration gets longer, and their travelling speeds become larger. (5) For the small IC case, an obvious oscillation of the surface wave amplitude (SWA) is observed, whereas for large IC model, the largest SWA only appears near the basin edge, and it is almost unchanged inside the basin. (6) The ratio of SWA to PGD decreases with the growing IC for the horizontal component, and the largest ratio occurs at the basin edge. However, this ratio is insensitive to IC for the vertical component, and it generally increases with larger distance from the basin edge.
- basin /
- identification of Rayleigh wave /
- impedance contrast /
- seismic ground motion /
- amplification effect

HTML全文

0. 引言

粗粒土是一种常见的筑坝材料。粗粒土剪切过程中的颗粒破碎现象明显^[1],这是引起堆石坝发生变形的重要原因之一。随着中国超高坝的建设,越来越多的学者开始关注高应力作用下粗粒土颗粒的破碎特性^[2-5]。但是,由于试验条件的限制,宏观试验只能根据破碎前后的级配曲线演化来推断颗粒破碎程度。与宏观试验相比,近年来日益成熟的离散元法（discrete element method,简称DEM）数值模拟为从细观层面对粗粒土颗粒破碎进行研究提供了新途径^[6-10]。

在DEM数值模拟中,颗粒强度和弹性力学参数是模拟颗粒破碎以及颗粒—颗粒、颗粒—边界相互作用的重要材料特性,是影响数值模拟结果的关键因素之一。目前主流的细观参数标定方法,通常是先假定一组细观参数,通过对参数及其组合的调整使数值试样的宏观力学表现不断逼近土体的真实行为,直到数值试验与室内试验得到的宏观力学性质曲线基本接近时,认为该组细观参数已具备一定合理性,可以用于后续的数值计算中。这种依托于使用者经验的“试错法”需进行多次尝试并有一定的盲目性。考虑到DEM数值模拟建立在细观颗粒间相互作用的基础上,通过物理力学试验获得颗粒强度和弹性力学参数的真实分布规律,可以为DEM数值模拟的细观参数标定提供规律性方面的参考和支撑。

粗粒土的DEM数值模拟中需要考虑的细观参数主要是颗粒强度和弹性模量,关于它们的研究主要集中在两个方面。一是颗粒参数的离散性。以颗粒强度为例,比如McDowell等^[11-12]提出用Weibull分布来描述颗粒强度的分布特点,但是迟世春等^[13]对石灰岩颗粒进行相同试验之后却发现用该分布拟合颗粒强度离散性的效果不佳；另外还有张明等^[14]提出用对数正态分布来描述颗粒强度的随机性在实际应用上更为合理,米晓飞等^[15]用Logistic函数对颗粒强度的随机分布特点进行了描述。上述关于颗粒参数离散性分布特征的研究都是在确定某一特定分布函数后对试验结果进行拟合,对于结果缺少在不同分布类型之间的对比选优。二是颗粒参数的尺寸效应。目前对于颗粒强度的尺寸效应研究很多,结果表明粗粒土颗粒强度与颗粒尺寸之间存在着较强的相关性,这种相关性通常用幂函数关系来表示^[12-13,16]；而对于颗粒弹性模量的尺寸效应研究不多。总体来说,国内外学者对于粗粒土颗粒强度的研究已取得较为丰富的成果；虽然关于粒状材料的弹性力学参数的研究案例并不少^[17-21],但是对于粗粒土颗粒的弹性力学参数进行研究的先例却不多；目前,对于粗粒土颗粒的研究主要集中在粒径60 mm以下的小尺寸范围,得到的尺寸效应模型能否适用于更大的粒径范围也值得探究。

本文基于20～120 mm的粗粒土颗粒单轴压缩试验结果,确定颗粒强度和弹性模量,用统计学中的K-S检验法从Weibull分布、Lognormal分布和Logistic分布中分别比选出它们的最优分布类型,给出它们各自的尺寸效应经验模型。然后采用240 mm粗粒土颗粒的试验结果对提出的尺寸效应经验模型进行验证。最后对颗粒刚度的特点进行了初步讨论。

1. 试验材料和方法

本试验采用爆破开采得到的大连石灰岩颗粒,按照粒径大小依次记为①～⑧组,粒径分别为20～24 mm、24～28 mm、28～32 mm、32～36 mm、36～40 mm以及60 mm、120 mm和240 mm。其中,①～⑤组颗粒由常规筛分得到,⑥～⑧组颗粒用特制的圆孔筛（直径分别为60±5,120±5,240±5 mm）挑选得到。为了减少颗粒形状对参数的影响,选取的颗粒几何形状相似,并剔除针状、扁平状等特殊颗粒。

由于石灰岩颗粒不是完全规则的球形,其尺寸仅用筛孔大小难以准确描述。试验时是将颗粒稳定放置在下刚性板上,并且进行多次试放,找到竖直高度最短的稳定放置状态,定义此时的高度为短轴H,并以此稳定状态进行轴向加载；在与H垂直的横截面中,取最大径为长轴L,与L垂直方向上的最大径为中轴W。此处的L、W和H互相垂直,并且满足 $L \geq W \geq H$ 。颗粒尺寸用算术平均径 $d_{a}$ 来衡量,各组颗粒的特征粒径用该组颗粒的算术平均径的均值表示,颗粒形状用球度S_p来描述：

$d_{a} = (L + W + H) / 3$ ,

(1)

$S_{p} = {(L \cdot W \cdot H)}^{1 / 3} / L \times 100 %$ 。

(2)

本文选择的石灰岩颗粒样本的各项基本物理参数详见表1。由于本文试验中各组颗粒样本的球度接近,可以认为形状对各组的影响是相同的。

表 1 石灰岩颗粒的基本物理参数

Table 1. Basic physical parameters of limestone particles

编号	粒组/mm	个数	算数平均径d_a/mm	球度S_p/%	质量m/g
①	20~24	82	22.13±1.97	74.07±7.53	11.24±2.90
②	24~28	78	25.83±2.03	76.54±7.49	18.10±3.72
③	28~32	76	30.17±2.25	74.34±6.99	26.50±5.99
④	32~36	77	33.81±2.43	75.70±7.49	37.26±7.89
⑤	36~40	76	37.32±2.88	75.99±7.13	48.57±9.81
⑥	60	35	53.89±4.48	77.98±6.68	183.52±31.40
⑦	120	38	120.99±8.31	77.30±6.25	2532.56±2928.13
⑧	240	20	225.35±16.42	78.80±5.07	13357.50±1884.72
注：表中格式为“均值±标准差”。

下载: 导出CSV

| 显示表格

由于本文试验所用石灰岩颗粒的粒径范围大,为保证试验顺利进行,①～⑤组颗粒使用图1（a）所示装置进行单轴压缩试验,⑥～⑧组颗粒使用图1（b）所示装置进行单轴压缩试验。上述两种装置的试验原理相同,加载方式可以采用位移控制或力控制,试验过程相当于上、下两个平行的刚性平面挤压颗粒直至破碎。这两种装置只有最大加载能力和刚性平面最大间距存在区别。

图 1 试验装置示意图

Figure 1. Schematic diagram of test instrument

下载: 全尺寸图片幻灯片

试验前将颗粒在烘箱内连续干燥6 h以上。将颗粒置于两刚性板间,通过控制位移施加轴向荷载,加载速率取0.5 mm/min,试验过程中自动记录荷载和位移。当观察到颗粒发生主体破坏后便停止加载,主体破坏是指颗粒产生贯穿型裂缝或分裂为几块。颗粒破碎前后的情况如图2所示,其荷载–位移曲线如图3所示。由于颗粒形状的不规则性会引起颗粒与刚性板之间的接触点附近产生应力集中,造成颗粒的局部压裂或者棱角破碎,反映在荷载–位移曲线上为荷载突然跌落,曲线呈现锯齿状。

图 2 颗粒破碎前后的照片

Figure 2. Photos of a particle before and after breakage

下载: 全尺寸图片幻灯片

图 3 石灰岩颗粒的荷载–位移曲线

Figure 3. Force-displacement curve of limestone particles

下载: 全尺寸图片幻灯片

2. 颗粒强度和弹性模量的确定

2.1 颗粒强度指标的确定

石灰岩颗粒强度指标由下式计算^[22]：

$σ_{c} = \frac{F_{f}}{d^{2}}$ ,

(3)

式中, $σ_{c}$ 为颗粒强度指标, $F_{f}$ 为颗粒破坏荷载,d为颗粒粒径,此处取每个颗粒的实际受力长度,即两刚性板之间的距离。

2.2 颗粒弹性模量的确定

文献[23]介绍了一种建立在固体力学中计算接触应力的赫兹理论的基础之上,用于计算质地相对坚硬且均匀的粒状材料弹性模量的方法。该方法所使用的试验手段和材料变形过程都与本文的试验研究极为相似,两刚性板的挤压是导致颗粒材料发生变形直至最后破坏的驱动力,所以本文采用该方法对石灰岩颗粒的弹性模量进行了计算。

上述方法将受到两刚性板挤压的不规则颗粒（如图4所示）的荷载–位移关系用下式表示：

图 4 不规则颗粒受压示意

Figure 4. Diagram of compression on an irregular particle

下载: 全尺寸图片幻灯片

$F = \frac{E}{0.338 K (1 - ν^{2})} \cdot s^{3 / 2}$ 。

(4)

式中 $F$ 为轴向荷载； $s$ 为轴向荷载 $F$ 作用下的变形量； $ν$ 为泊松比,本文根据文献[24]中对各类岩石泊松比的汇总,假设石灰岩的泊松比 $ν = 0.25$ ； $E$ 为颗粒弹性模量；K为和颗粒接触点曲率有关的参数,引入该参数是因为颗粒表面粗糙导致接触点附近并非绝对光滑且连续,

$K = {[K_{U} {(\frac{1}{R_{U}} + \frac{1}{{R^{'}}_{U}})}^{1 / 3} + K_{L} {(\frac{1}{R_{L}} + \frac{1}{{R^{'}}_{L}})}^{1 / 3}]}^{3 / 2}$ 。

(5)

式中 ${R^{'}}_{U}$ , $R_{U}$ 分别为颗粒与上刚性板接触点处的最大和最小曲率半径； ${R^{'}}_{L}$ , $R_{L}$ 分别为颗粒与下刚性板接触点处的最大和最小曲率半径； $K_{U}$ , $K_{L}$ 为主曲率半径决定的常数,通过计算 $\cos θ$ ,可以从表2中对应查取, $θ$ 为颗粒表面与刚性板接触点处接触主平面的夹角（°）,根据赫兹接触理论有 $K_{U}$ 和 $K_{L}$ 分别对应的 $\cos θ$ 表达式为

表 2 不同的θ对应的K_U（K_L）值（节选）^[23]

Table 2. Values of K_U (K_L) for various values of θ (excerpts)^[23]

θ/(°)	50	55	60	…	80	85	90
cos θ	0.6428	0.5736	0.5000	…	0.1736	0.0872	0.0
K_U(K_L)	1.198	1.235	1.267	…	1.342	1.349	1.351

下载: 导出CSV

| 显示表格

$\begin{array}{l} K_{U} ： & \cos θ = (1 / R_{U} - 1 / {R^{'}}_{U}) / (1 / R_{U} + 1 / {R^{'}}_{U}) & , \\ K_{L} ： & \cos θ = (1 / R_{L} - 1 / {R^{'}}_{L}) / (1 / R_{L} + 1 / {R^{'}}_{L}) & 。 \end{array}}$

(6)

具体结合本文试验,石灰岩颗粒在自重下处于自稳定状态。可以认为颗粒与下刚性板之间近似面面接触,与上刚性板之间近似点面接触。这种情况下,颗粒与下刚性板接触点处的曲率 ${R^{'}}_{L} = R_{L} = \infty$ 。此时可以将式（4）具体写成

$F = \frac{E}{0.338 (1 - ν^{2}) {[K_{U} {(1 / R_{U} + 1 / {R^{'}}_{U})}^{1 / 3}]}^{3 / 2}} \cdot s^{3 / 2}$ ,

(7)

式中, ${R^{'}}_{U}$ , $R_{U}$ 由颗粒的L,W和H计算^[18]：

${R^{'}}_{U} = (L^{2} / 4 + H^{2}) / (2 H)$ ,

(8)

$R_{U} = (W^{2} / 4 + H^{2}) / (2 H)$ ,

(9)

继续将式（7）简写为

$F = C_{H} \cdot s^{3 / 2}$ ,

(10)

式中, $C_{H}$ 可以由颗粒破坏前的荷载–位移曲线拟合得到。因而,颗粒弹性模量E如下所示：

$E = 0.338 C_{H} (1 - ν^{2}) {[K_{U} {(\frac{1}{R_{U}} + \frac{1}{{R^{'}}_{U}})}^{1 / 3}]}^{3 / 2}$ 。

(11)

3. 数理统计和分析

3.1 参数的数理统计方法

本文首先采用格布拉斯准则^[25]检测样本中的异常值。设 $X = (X_{1}, X_{2}, \dots, X_{n})$ 是待检测数据,如果最值 $X_{i}$ 满足下式则为异常值,应予剔除。

$\frac{| X_{i} - \bar{X} |}{S} \geq G (N, α)$ 。

(12)

式中 $\bar{X}$ 和 $S$ 分别为样本均值和标准差； $G$ 为格拉布斯临界值,根据样本容量 $N$ 和显著性水平 $α$ 查表^[25]得到。在剔除某一异常值后,应继续对余下的样本点进行检测,直到没有异常值为止。

然后根据已有研究经验^[11-17],本文尝试用Weibull分布、Lognormal分布和Logistic分布对颗粒强度 $σ_{c}$ 和弹性模量E分别进行统计。

最后对于每个参数,使用K-S检验法^[26]定量地判断假设的概率分布类型是否合适,并从中确定最优分布形式。该方法通过将选定的分布类型的理论累积概率与观察到的经验累积概率进行比较,找出它们之间最大的差值,并参照抽样分布,给出这一差异是否处于偶然。如果两者较为接近,则表明实际样本的分布类型与假设的理论分布类型拟合程度很高。所有的统计分析均在显著性水平 $α = 0.05$ 的条件下进行,即置信度为95%。

3.2 参数的最优分布类型

采用式（3）,（11）对各粒组的颗粒强度 $σ_{c}$ 和弹性模量E进行整理,绘制参数统计直方图,并采用K-S检验法分别对3种假设分布类型进行了检验。其中,28～32 mm粒组的参数统计直方图和最优概率密度曲线如图5所示,限于篇幅,其他粒组略。各粒组的K-S检验结果详见表3,结果表明：①参数 $σ_{c}$ 和E对于Weibull分布、Lognormal分布和Logistic分布都可接受；②对参数 $σ_{c}$ 和E可以直接判定最优分布类型是Lognormal分布。

图 5 石灰岩颗粒参数统计直方图和最优概率密度曲线

Figure 5. Statistical histograms and optimal probability density functions of parameters for limestone particles

下载: 全尺寸图片幻灯片

表 3 石灰岩颗粒强度和弹性模量分布类型的K-S检验

Table 3. K-S test results of distribution types for strength and elastic modulus of limestone particles

编号	粒组/mm	颗粒强度					弹性模量
编号	粒组/mm	均值/MPa	分布形式	K-S值	判断	最优分布	均值/MPa	分布形式	K-S值	判断	最优分布
①	20~24	13.108	Weibull	0.085	满足	Lognormal	1005.193	Weibull	0.097	满足	Lognormal
			Lognormal	0.055	满足			Lognormal	0.073	满足
			Logistic	0.068	满足			Logistic	0.103	满足
②	24~28	12.389	Weibull	0.092	满足	Lognormal	1113.994	Weibull	0.095	满足	Lognormal
			Lognormal	0.062	满足			Lognormal	0.089	满足
			Logistic	0.096	满足			Logistic	0.092	满足
③	28~32	11.977	Weibull	0.078	满足	Lognormal	928.598	Weibull	0.073	满足	Lognormal
			Lognormal	0.056	满足			Lognormal	0.072	满足
			Logistic	0.089	满足			Logistic	0.085	满足
④	32~36	11.673	Weibull	0.128	满足	Lognormal	839.674	Weibull	0.100	满足	Lognormal
			Lognormal	0.112	满足			Lognormal	0.067	满足
			Logistic	0.126	满足			Logistic	0.084	满足
⑤	36~40	10.438	Weibull	0.084	满足	Lognormal	801.380	Weibull	0.102	满足	Lognormal
			Lognormal	0.040	满足			Lognormal	0.084	满足
			Logistic	0.077	满足			Logistic	0.126	满足
⑥	60	6.442	Weibull	0.113	满足	Lognormal	544.306	Weibull	0.135	满足	Lognormal
			Lognormal	0.079	满足			Lognormal	0.096	满足
			Logistic	0.089	满足			Logistic	0.138	满足
⑦	120	5.242	Weibull	0.103	满足	Lognormal	422.451	Weibull	0.169	满足	Lognormal
			Lognormal	0.048	满足			Lognormal	0.107	满足
			Logistic	0.076	满足			Logistic	0.143	满足
⑧	240	3.394	Weibull	0.117	满足	Lognormal	281.528	Weibull	0.125	满足	Lognormal
			Lognormal	0.084	满足			Lognormal	0.119	满足
			Logistic	0.126	满足			Logistic	0.121	满足

下载: 导出CSV

| 显示表格

3.3 参数的尺寸效应模型

为进一步研究颗粒强度和弹性模量与粒径的相关性,选择参数均值作为其代表值绘制于图6中。由图6可知这两个参数与颗粒尺寸之间存在着明显的非线性相关性。为了能够简单明了地描述这一关系,采用式（13）的幂函数表达式对这一关系进行了拟合,并且将拟合结果作为参数的尺寸效应经验模型,拟合结果详见表4。

图 6 石灰岩颗粒参数的尺寸效应曲线

Figure 6. Curves of size effect of parameters for limestone particles

下载: 全尺寸图片幻灯片

表 4 参数的尺寸效应模型

Table 4. Models for size effect of parameters

参数名称	代表值含义及符号	尺寸效应模型	r²	预测误差/%
颗粒强度	均值 $σ_{0}$	$σ_{0} =89 .71 {\bar{d}}_{a}^{- 0.606}$	0.92	0.58
弹性模量	均值 $E_{0}$	$E_{0} = 7351 {\bar{d}}_{a}^{- 0.615}$	0.91	6.61

下载: 导出CSV

| 显示表格

$y = λ {\bar{d}}_{a}^{n}$ 。

(13)

式中 $y$ 为待研究参数代表值； ${\bar{d}}_{a}$ 为颗粒算数平均径的均值； $λ$ 和 $n$ 为拟合参数。为了验证本文所给的参数尺寸效应经验模型是否准确,对240 mm的颗粒试验结果进行了预测,颗粒强度 $σ_{c}$ 、弹性模量E的预测值和试验值之间的相对误差分别为0.58%,6.61%,在可接受范围内。这表明,本文所给出的参数尺寸效应经验模型能够适用于更大的颗粒尺寸范围。尺寸效应经验模型的n值小于0说明大连石灰岩的颗粒强度和弹性模量的均值和颗粒尺寸之间呈负相关。该结果和前人统计结果一致^[12-13,17],同时弥补了对大尺寸不规则颗粒单轴压缩试验结果进行统计分析的空白。

4. 讨论

前文讨论了颗粒强度和弹性模量的随机分布规律和尺寸效应模型,除了上述两个参数外,颗粒刚度也是DEM数值模拟中需要考虑的重要参数之一。对于刚度的认识有两种：①认为刚度是线性的；②认为刚度是非线性的。而目前多把颗粒刚度看作是线性的。为了分析线性刚度和非线性刚度哪个更加符合实际情况,这里对石灰岩颗粒在破坏点之前的荷载—位移曲线进行了线性拟合（ $F = k s$ ）和非线性拟合（ $F = C_{H} s^{3 / 2}$ ）结果的对比,如图7所示。通过对每个颗粒线性拟合和非线性拟合结果的 $r^{2}$ 进行比较,发现本文试验有81.74%的颗粒用非线性拟合比线性拟合效果更好。这说明,在石灰岩颗粒受单轴压缩过程中,颗粒刚度用非线性来描述更加符合实际。

图 7 石灰岩颗粒荷载–位移曲线的线性拟合和非线性拟合结果对比

Figure 7. Comparison between linear fitting and nonlinear fitting results of load-displacement curves for limestone particles

下载: 全尺寸图片幻灯片

5. 结论

本文通过大量大连石灰岩颗粒单轴压缩试验,获得了颗粒强度和弹性模量的随机分布特征和尺寸效应经验模型,并对颗粒刚度的特点进行了初步讨论。这些统计结果反映了粗粒土颗粒在受力变形过程中的力学规律。建议在进行粗粒土DEM数值模拟时,对这些规律加以考虑。

（1）不仅粗粒土颗粒强度具有离散性,而且颗粒弹性模量同样具有离散性,该情况说明粗粒土颗粒在力学特性上表现出固有的离散性。

（2）大连石灰岩颗粒强度和弹性模量的最优概率分布类型是Lognormal分布。

（3）大连石灰岩颗粒强度和弹性模量的均值均与颗粒尺寸之间呈负相关,用幂函数拟合效果较好。可见,粗粒土颗粒强度和弹性模量都具有明显的尺寸效应。

（4）在石灰岩颗粒单轴压缩过程中,颗粒刚度用非线性来描述更加符合实际。

图 1 盆地地表观测点的模拟时程及提取Rayleigh波时程

Figure 1. Simulated seismograms and extracted Rayleigh waves for observation points

下载: 全尺寸图片幻灯片

图 2 模拟及提取面波时程的f-k谱

Figure 2. f-k spectra for simulated seismograms and extracted Rayleigh waves

下载: 全尺寸图片幻灯片

图 3 二维盆地计算模型（黑色圆点表示代表性的台站位置）

Figure 3. 2D basin model for investigations (solid circles-representative stations)

下载: 全尺寸图片幻灯片

图 4 输入波时程及其傅里叶谱

Figure 4. Time histories of input waves and their Fourier spectra

下载: 全尺寸图片幻灯片

图 5 不同阻抗比模型对应的盆地地表观测点水平（左）和垂直(右)分量的模拟位移时程

Figure 5. Time histories of horizontal (left) and vertical (right) components for ground points of different IC models

下载: 全尺寸图片幻灯片

图 6 不同阻抗比模型对应的盆地地表观测点的位移峰值分布

Figure 6. PGD distributions for ground points of different IC models

下载: 全尺寸图片幻灯片

图 7 不同阻抗比模型对应的盆地地表观测点的放大系数分布

Figure 7. Amplification factor distributions for ground points of different IC models

下载: 全尺寸图片幻灯片

图 8 不同阻抗比模型对应的盆地地表观测点Rayleigh面波水平（左）和垂直（右）分量的位移时程

Figure 8. Time histories of Raleigh wave of horizontal (left) and vertical (right) components for ground points of changed IR models

下载: 全尺寸图片幻灯片

图 9 不同阻抗比模型的盆地内地表观测点次生Rayleigh面波的位移峰值分布

Figure 9. Amplitude distributions of basin-induced Rayleigh waves for ground points of different IC models

下载: 全尺寸图片幻灯片

图 10 IC=0.044模型对应的不同时刻水平分量的位移波场快照（黑色实线之内为盆地）

Figure 10. Snapshots of horizontal component displacement wavefield for IC=0.044 model (black line-basin boundary)

下载: 全尺寸图片幻灯片

图 11 不同阻抗比模型的盆地内地表观测点次生Rayleigh面波的幅值与地震动峰值的比值

Figure 11. Distributions of ratio of amplitudes of basin-induced Rayleigh waves to PGDs of ground points for different IC models

下载: 全尺寸图片幻灯片

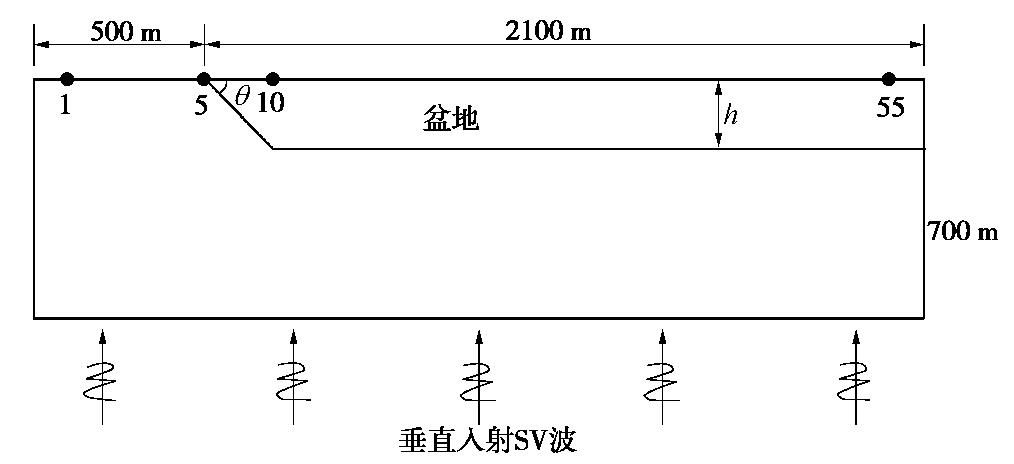
表 1 计算模型介质参数

Table 1 Physical parameters of model

类型剪切波速V_s/(m·s^-1) 压缩波速V_p/(m·s^-1) 密度/(kg·m^-3)

盆地 200~1500 2V_s 1700
基岩 3000 5196 2600

下载: 导出CSV

表 2 不同阻抗比模型模拟得到的盆地地表水平和垂直分量的PGD最大值及二者的比值

Table 2 Maximum values and ratios of PGDs of horizontal to vertical components of changed IC models

IC 水平分量位移最大值dx/m 垂直分量位移最大值dy/m dy/dx

0.044 4.02 2.99 0.74
0.076 4.23 3.18 0.75
0.109 4.11 3.05 0.74
0.164 3.79 2.22 0.59
0.218 3.62 1.54 0.43
0.327 3.19 0.83 0.26

下载: 导出CSV

参考文献(26)

[1]	刘烁宇, 李英民. 盆地型长周期地震动的判别准则[J]. 湖南大学学报(自然科学版), 2018, 45(5): 85-93. doi: 10.16339/j.cnki.hdxbzkb.2018.05.010 LIU Shuo-yu, LI Ying-min. Discriminant criterion of long-period ground motion in basin[J]. Journal of Hunan University (Natural Science), 2018, 45(5): 85-93. (in Chinese) doi: 10.16339/j.cnki.hdxbzkb.2018.05.010
[2]	ANDERSON J G, BODIN P, BRUNE J N, et al. Strong ground motion from the Michoacan, Mexico, Earthquake[J]. Science, 1986, 233(4768): 1043-1049. doi: 10.1126/science.233.4768.1043
[3]	KAWASE H. The cause of the damage belt in Kobe: “The basin-edge effect,” constructive interference of the direct S-wave with the basin-induced diffracted/Rayleigh waves[J]. Seismological Research Letters, 1996, 67(5): 25-34. doi: 10.1785/gssrl.67.5.25
[4]	李雪强. 沉积盆地地震效应研究[D]. 北京: 中国地震局工程力学研究所, 2011. LI Xue-qiang. Study on Seismic Effect of Sedimentary Basin[D]. Beijing: Institute of Engineering Mechanics, China Earthquake Administration, 2011. (in Chinese)
[5]	YUAN Y F, YANG B P, HUANG S D. Damage distribution and estimation of ground motion in Shidian (China) basin[C]//Proceedings of the International Symposium on the Effects of Surface Geology on Seismic Motion, 1992, Odawara.
[6]	ROTEN D, FÄH D, CORNOU C, et al. Two-dimensional resonances in Alpine valleys identified from ambient vibration wavefields[J]. Geophysical Journal International, 2006, 165(3): 889-905. doi: 10.1111/j.1365-246X.2006.02935.x
[7]	BOUÉ P, DENOLLE M, HIRATA N, et al. Beyond basin resonance: characterizing wave propagation using a dense array and the ambient seismic field[J]. Geophysical Journal International, 2016, 206(2): 1261-1272. doi: 10.1093/gji/ggw205
[8]	LIU Q, YU Y, YIN D, et al. Simulations of strong motion in the Weihe basin during the Wenchuan earthquake by spectral element method[J]. Geophysical Journal International, 2018, 215(2): 978-995. doi: 10.1093/gji/ggy320
[9]	FRANKEL A, HOUGH S, FRIBERG P, et al. Observations of Loma Prieta aftershocks from a dense array in Sunnyvale, California[J]. Bull Seism Soc Am, 1991, 81(5): 1900-1922. doi: 10.1785/BSSA0810051900
[10]	ABRAHAM J R, LAI C G, PAPAGEORGIOU A. Basin-effects observed during the 2012 Emilia earthquake sequence in Northern Italy[J]. Soil Dynamics and Earthquake Engineering, 2015, 78: 230-242. doi: 10.1016/j.soildyn.2015.08.007
[11]	王季. 基于F-K变换的井下多道瑞利波频散曲线提取[J]. 煤田地质与勘探, 2012, 40(2): 75-77. https://www.cnki.com.cn/Article/CJFDTOTAL-MDKT201202020.htm WANG Ji. Dispersive curve extraction of Rayleigh wave in coal mine based on F-K transform[J]. Coal Geology and Exploration, 2012, 40(2): 75-77. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MDKT201202020.htm
[12]	雍凡, 罗水余, 李颜贵, 等. F-K变换与预测反褶积压制多次波效果对比[J]. 物探化探计算技术, 2014, 36(6): 700-707. https://www.cnki.com.cn/Article/CJFDTOTAL-WTHT201406010.htm YONG Fan, LUO Shui-yu, LI Yan-gui, et al. Comparisons of F-K domain methods and prediction deconvolution for multiple attenuation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2014, 36(6): 700-707. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WTHT201406010.htm
[13]	PINNEGAR C R. Polarization analysis and polarization filtering of three-component signals with the time-frequency S transform[J]. Geophysical Journal International, 2006, 165(2): 596-606. doi: 10.1111/j.1365-246X.2006.02937.x
[14]	GALIANA-MERINO J J, PAROLAI S, ROSA-HERRANZ J. Seismic wave characterization using complex trace analysis in the stationary wavelet packet domain[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(11): 1565-1578. doi: 10.1016/j.soildyn.2011.06.009
[15]	MEZA-FAJARDO K C, PAPAGEORGIOU A S, SEMBLAT J F. Identification and extraction of surface waves from three-component seismograms based on the normalized inner product[J]. Bulletin of the Seismological Society of America, 2015, 105(1): 210-229. doi: 10.1785/0120140012
[16]	MEZA-FAJARDO K C, PAPAGEORGIOU A S. Estimation of rocking and torsion associated with surface waves extracted from recorded motions[J]. Soil Dynamics and Earthquake Engineering, 2016, 80: 225-240. doi: 10.1016/j.soildyn.2015.10.017
[17]	MEZA-FAJARDO K C, VARONE C, LENTI L, et al. Surface wave quantification in a highly heterogeneous alluvial basin: case study of the Fosso di Vallerano valley, Rome, Italy[J]. Soil Dynamics and Earthquake Engineering, 2019, 120: 292-300. doi: 10.1016/j.soildyn.2019.02.008
[18]	ZHANG Z, SUN Y, BERTEUSSEN K. Analysis of surface waves in shallow water environment of the Persian Gulf using S and t-f-k transform[M]//SEG Technical Program Expanded Abstracts 2010. Society of Exploration Geophysicists, 2010: 3723-3727.
[19]	WANG C, WANG Y. Ground roll attenuation using polarization analysis in the t-f-k domain[J]. Geophysical Journal International, 2017, 210(1): 240-254. doi: 10.1093/gji/ggx152
[20]	NARAYAN J P. Effects of angle of incidence of SH-wave at the basin-edge on the characteristics of basin edge induced Love wave[J]. J Earthq Tsunami, 2012, 6(1): 1250006. doi: 10.1142/S1793431112500066
[21]	NARAYAN J P. Effects of P-wave and S-wave impedance contrast on the characteristics of basin transduced Rayleigh waves[J]. Pure and Applied Geophysics, 2012, 169(4): 693-709. doi: 10.1007/s00024-011-0338-7
[22]	LIU Q, YU Y, ZHANG X. Three-dimensional simulations of strong ground motion in the Shidian basin based upon the spectral-element method[J]. Earthquake Engineering and Engineering Vibration, 2015, 14(3): 385-398.
[23]	MOCZO P, KRISTEK J, BARD P Y, et al. Key structural parameters affecting earthquake ground motion in 2D and 3D sedimentary structures[J]. Bulletin of Earthquake Engineering, 2018, 16(6): 2421-2450.
[24]	李一琼. 基于SDSCD数值算法完善与盆地表征模型模拟[D]. 北京: 中国地震局地球物理研究所, 2014. LI Yi-qiong. The Numerical Algorithm Perfection of SDSCD and Simulation on Basin Characteristic Model[D]. Beijing: Institute of Geophysics, China Earthquake Administration, 2014. (in Chinese)
[25]	刘中宪, 黄磊, 梁建文. 三维局部场地对地震波的散射IBIEM-FEM耦合模拟[J]. 岩土工程学报, 2017, 39(2): 301-310. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201702017.htm LIU Zhong-xian, HUANG Lei, LIANG Jian-wen. FEM-IBIEM coupled method for simulating scattering of seismic waves by 3-D complex local site[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(2): 301-310. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201702017.htm
[26]	廖振鹏. 工程波动理论导论[M]. 北京: 科学出版社, 2002. LIAO Zhen-peng. Introduction to Wave Motion Theories in Engineering[M]. Beijing: Science Press, 2002. (in Chinese)

施引文献(12)

期刊类型引用(4)

1.	罗仁宇，李奇志，祖公博，黄云进，杨耿超，姚清河. 基于卷积神经网络的超分辨率格子Boltzmann方法研究. 力学学报. 2024(12): 3612-3624 . 百度学术
2.	侯娟，滕宇阳，李昊，刘磊. 多孔介质曲折度对膨润土衬垫渗透性能的影响. 湖南大学学报(自然科学版). 2022(01): 155-164 . 百度学术
3.	陈经明，周泽超，陈茜茜，李寻，罗跃. 酸法地浸采铀多井系统中渗透系数时空演化模拟. 有色金属科学与工程. 2022(03): 106-116 . 百度学术
4.	吴志平，刘波平，王康，李石滨，胡毕炜，胡必伟，游杰. 基于高性能计算的离散介质冲击过程. 计算机与现代化. 2022(10): 41-46 . 百度学术