0.   引言

土作为多孔多相材料,其体积会随着剪切作用,发生膨胀或压缩,这种性质被称作剪胀（剪缩）性^[1]。剪胀性是土区别于其他材料的重要特性^[2],是建立本构模型的基础^[3]。国外学者针对土的剪胀性开展了大量研究。1885年Reynolds^[4]提出砂土的剪胀特性与粒子之间的跨越现象有关。1962年Rowe^[5]提出应力剪胀理论,认为剪胀是由内部几何约束引起的,并得到了广泛的应用。随着研究的深入,学者们发现砂土的剪胀率还与其材料状态^[6]密切相关。Been等^[7]提出了描述粗粒土剪胀变形的状态参数,Cubrinovski等^[8]通过试验分析,发现塑性剪应变会影响剪胀率的变化。Li等^[9]将剪胀性与材料的当前状态紧密联系起来。Antonio等^[10]利用改进后的应力剪胀理论建立了各向同性的弹塑性模型。Fern等^[11]将改进后的应力剪胀理论推广到非饱和土的研究中。Patil等^[12]对静态压实粉砂的剪胀性进行了全面的分析,并揭示了峰值应力比与剪胀率的关系。国内学者同时也取得了丰富的研究成果。李广信等^[13]认为,土的剪胀变化是土颗粒从低能状态向高能状态的变化过程,其大部分剪胀会随着卸荷而恢复。张建民^[14]认为砂土存在可逆性剪胀是相对滑移机制和平均定向率的可逆变化共同作用的结果。刘元雪等^[15]提出土体的可恢复性剪胀可部分归因于土的各向异性引起的弹性剪胀。迟明杰等^[16]基于细观力学的思想,对砂土剪胀机理开展了探索,并得到了新的剪胀模型。熊焕等^[17]利用非共轴因子的优化剪胀方程,使得Rowe剪胀模型适用于主应力轴旋转等更加复杂的加载条件。孙逸飞等^[18]基于分数阶梯度律,从理论层面提出了分数阶状态依赖剪胀方程。陆勇等^[19]通过引入应力路径相关因子来修正塑性应变增量中与应力路径相关的部分,从而使得模型硬化参量能够反映密实砂土在常压下的剪胀特性。刘斯宏等^[20]假定堆石料存在唯一的临界状态面,对剪胀模型与硬化参数进行了修正。Li等^[21]在对粉质黏土的三轴试验中,发现了剪胀率与塑性剪应变之间存在明显的非线性特征。

学者们从能量、状态参数和微观组构等角度来解释剪胀机理,并建立了大量模型,但这些模型的通用性却不尽人意。这个事实表明,对土的剪胀性问题的复杂性,并未找到它的症结所在。笔者认为主要是当前建立的剪胀模型并未对土的剪胀特性的共同规律进行深入研究所致。

土的剪胀性问题比较复杂。根据土在剪切作用下的体积变化过程,将其分为剪缩型土和剪胀型土。剪缩型土在剪切作用下,只发生压缩变形；剪胀型土在剪切作用下,先发生压缩变形,达到相变状态后,再发生膨胀变形。它们的力学机制与计算模型大不相同,剪缩型土的剪胀特性将另文研究,因此本文只研究剪胀型土的剪胀特性与计算模型。近年来,大数据深度挖掘技术在岩土工程的规律发现与特征提取上表现了突出的能力^[22-24],表明了大数据技术在土的剪胀性研究上是可行的。本文的主要目的是利用大数据深度挖掘技术,建立一个能反映剪胀型土的剪胀性共同规律的剪胀模型。首先基于Hadoop+Spark的大数据计算平台,对大量剪胀型土的剪胀性试验数据进行特征挖掘,建立了剪胀率与其各影响因素之间的相关性函数。在此基础上,根据其基本力学特性,建立了剪胀模型。通过模型的检验,验证了模型的科学性和合理性。

1.   一种分布式处理的DLMR算法

在本文研究中,需要对剪胀性大数据特征进行深度挖掘,重点是在剪胀率与其影响因素之间开展大数据回归分析。通过调研可知,传统回归算法存在着收敛性慢,计算不稳定以及在处理大规模数据时效率低下等问题。为了解决以上问题,本文提出了一种基于Hadoop+Spark大数据平台的（distributed levenberg marquardt regression）DLMR算法。

1.1   Levenberg-Marquardt（LM）算法

在进行回归分析时,多采用Gradient Descent（GD）法和Gauss-Newton（GN）法,但GD法在远离极小值时下滑很快,而在接近极小值时下滑却很慢,并且在靠近极小值时呈Z型下降,容易导致误差变大。GN法在某些情况下,其后续迭代值会出现大于前序迭代值的情况,从而造成回归失败。在LM^[25]算法中,当学习参数$\lambda$很小时,步长等于GN法步长,当$\lambda$很大时,步长约等于GD法的步长,LM算法结合了GD法和GN法的优点,同时解决了收敛性慢等问题。因此在对数据进行回归处理时,LM算法能够表现出良好的性能。

1.2   基于Hadoop+Spark的分布式计算平台

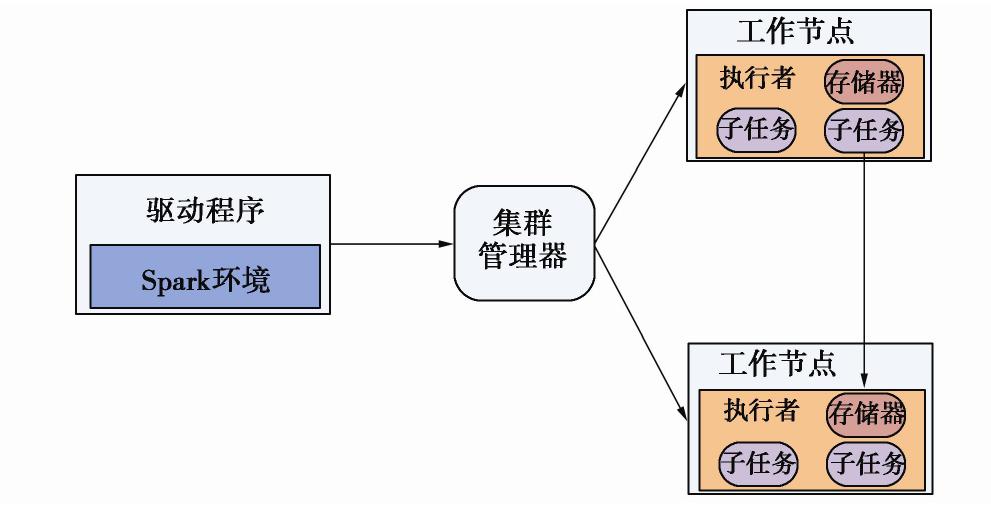
Hadoop是一个用于分布式计算的大数据处理平台,主要由分布式文件存储系统（HDFS）和MapReduce框架构成。在本文研究中,海量试验数据被存储在HDFS中,一方面实现了试验数据的分布式存储,保证了数据的安全性；另一方面也为后续的分布式计算提供了数据平台,提高了数据挖掘的效率。Spark与其他大数据架构的最大区别是基于内存而进行数据计算,因此可高效地在内存中直接对目标数据进行复杂批量处理。Spark^[26]的架构组成如图1所示。

图  1  Spark的架构组成

Figure  1.  Architectural composition of Spark

下载: 全尺寸图片 幻灯片

其中,Cluster Manager可视作Master主节点,负责控制整个集群,并监控Worker的工作。Worker Node视作从节点,负责控制具体的计算节点以及Executor。Driver负责运行某个Application的函数。Executor视作执行器,是某个Application运行在Worker Node上的一个进程。基本原理是将目标数据划分为若干块,再交由Cluster Manager分配给各Worker Node节点计算,完成运算后,再进行组合,从而得到最终结果。在传统回归算法中,每次迭代都必须要遍历所有数据,导致计算效率低下。采用Hadoop+Spark的分布式计算平台可让集群中的多个工作节点共同参与到运算过程中,从而大大提高计算稳定性和运行效率。

1.3   基于Hadoop+Spark的LM算法

在本文中引入了LM算法的思想,又因为回归问题可转化为非线性最小二乘问题,所以在进行迭代运算时,首先用信赖域的方法计算惩罚因子$\mu$,并将其置于迭代步长中。本文算法的迭代公式如下所示：

式中,$h_{lm}$.为迭代步长,$J_{\text{r}}$为雅可比矩阵。

在描述本文提出的算法之前,再对部分记号进行说明。$J^k=\nabla \mathrm{F}(x^k)$表示函数$F$在$x^k$处的雅可比矩阵,将$J^k$的列分成t组$J_1^k,J_{\text{2}}^k,\cdots ,J_t^k$,其中$J_i^k$是$m\times n_i$的矩阵。又记$x_{\text{1}}\in R^{{\text{n}}_1},x_{\text{2}}\in R^{{\text{n}}_{\text{2}}},\cdots ,x_t\in R^{{\text{n}}_t}$。设$J_i^k$是由$J^k$的第$j_1,j_2,\cdots ,j_i$列构成,记$\overline{x_i}$表示用$x_i$的元素代替n维零向量相应于$j_1,j_2,\cdots ,j_i$的零元素所形成的n维向量。结合1.1和1.2节内容,可将LM算法在Hadoop+Spark的分布式计算平台下实现,步骤如下所示：①首先定初始值$x^{\text{1}},k=1,i=1,r^k=F(x^k)$；②计算$J_i^k=\nabla \mathrm{F}{(x^k)}_i,i=1,2,\cdots ,t$；③计算$s_i^k$,$\min \text{{||}{J}_i^k{s}_i+$$r^{k+(i-1)/t}{\text{||}}_{\text{2}};s_j\in R^{n_i}\text{}},i=1,2,\cdots ,t$；④计算$w_i,i=1,2,\cdots ,t$；⑤计算$r^{k+1}=r^k+{\displaystyle \sum w_i{J}_i^k{s}_i^k}$；⑥计算$x^{k+1}=x^k+$${\displaystyle \sum w_i{\overline{s}}_i^k}$；⑦当迭代完成或满足收敛条件时,运算结束,得到最优的回归训练参数,否则令$k=k+\text{1}$,转到步骤②,重复进行。通过对本文算法分析可知,步骤②、③和④具有完全的可并行性,另在步骤⑤和⑥中,可让t个工作节点分别计算$r^{k+1}$和$x^{k+1}$的分量,所以本文提出的分布式DLMR算法具有良好的并行性。另在本文研究中,集群平台的环境配置如表1所示。

表  1  基于Hadoop的Spark大数据计算平台环境配置

Table  1.  Environment configuration of Spark big data computing platform based on Hadoop

软件名称	版本
Hadoop	2.6.2
Spark	1.5.2
Scala	2.10.4
Java	jdk1.7.0_79
Ubuntu	14.04

下载: 导出CSV 

| 显示表格

2.   基于剪胀性的大数据特征和DLMR算法的剪胀模型

2.1   剪胀性大数据的来源

剪胀性数据的可靠性和规模性是保证本文研究的重要条件,因此在对数据进行筛选时需要严格按照如下标准施行。

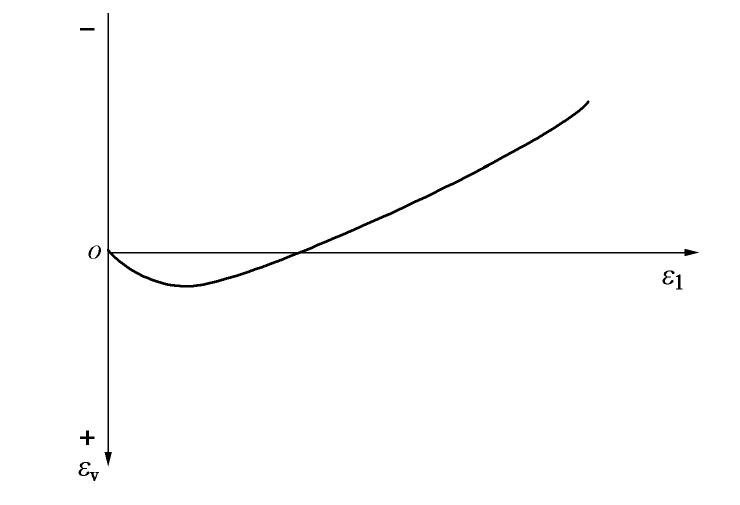
（1）由于本文针对的是剪胀型土的研究,所以选择的土样本的体应变${\epsilon }_{\text{v}}$随轴向应变${\epsilon }_1$的变化趋势需要符合图2中曲线所示。

图  2  剪胀型土${\epsilon }_{\text{v}}$与${\epsilon }_1$的关系

Figure  2.  Relationship between ${\epsilon }_{\text{v}}$ and ${\epsilon }_1$ of dilatant soil

下载: 全尺寸图片 幻灯片

（2）应力路径对土的剪胀特性的影响比较复杂。课题组考虑到常规三轴压缩试验在实际应用中较为普遍,数据丰富并且较易获取；另一方面常规三轴压缩试验的应力路径较为简单。因此在本文研究中要求试验数据必须来源于常规三轴压缩试验的土样本。

（3）在提取试验数据点时,必须按照实际的试验点进行提取。其中在剪缩阶段的试验点要求不少于10个,在剪胀阶段的试验点要求不少于15个。

前期,课题组已从国内外具有重要影响的学术刊物中搜集了约500篇关于土的剪胀性的文献资料,主要来源期刊见表2。

表  2  文献主要来源表

Table  2.  Main sources of literatures

中文期刊	外文期刊
《岩土工程学报》	《GEOTECHNIQUE》
《岩石力学与工程学报》	《SOILS FOUND》
《岩土力学》	《INT J GEOMECH》
《土木工程学报》	《J GEOTECH GEOENVIRON》

下载: 导出CSV 

| 显示表格

为了保证本文研究中数据来源的可靠性,同时避免数据提取中存在的误差影响,将课题组分为两个小组,严格按照上述的数据筛选标准分别进行核查,最终得到155个剪胀型土样本,并从中提取计算出相关的试验数据如表3所示,其中剪胀率$d$,为塑性体应变增量$\text{d}{\epsilon }_{\text{v}}^{\text{p}}$与塑性剪应变增量$\text{d}{\epsilon }_s^p$的比值,可作为评价剪胀性的重要指标,当$d>0$时,土体为剪缩变形；当$d<0$时,土体为剪胀变形。

表  3  部分土样本的数据

Table  3.  Data of some soil samples

样本编号	实验序列点	$d$	$p$	$q$	$\text{d}p$	$\text{d}q$	${\epsilon }_{\text{v}}^p$	${\epsilon }_{\text{s}}^p$	$\cdots$
S-1	1	0.67	715.12	795.28	40.23	120.69	0.0026	0.0039	$⋮$
	2	0.44	745.43	886.28	30.32	90.96	0.0048	0.0089	$⋮$
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
	24	-0.02	820.84	1112.52	-2.51	-7.53	0.0056	0.0931	$⋮$
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
CN-5	1	0.85	283.51	400.53	38.38	115.14	0.0007	0.0008	$⋮$
	2	0.63	333.14	549.44	49.63	148.90	0.0012	0.0016	$⋮$
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
	28	-0.09	417.40	802.21	-5.90	-17.72	-0.0164	0.0631	$⋮$

下载: 导出CSV 

| 显示表格

2.2   剪胀率的影响因素

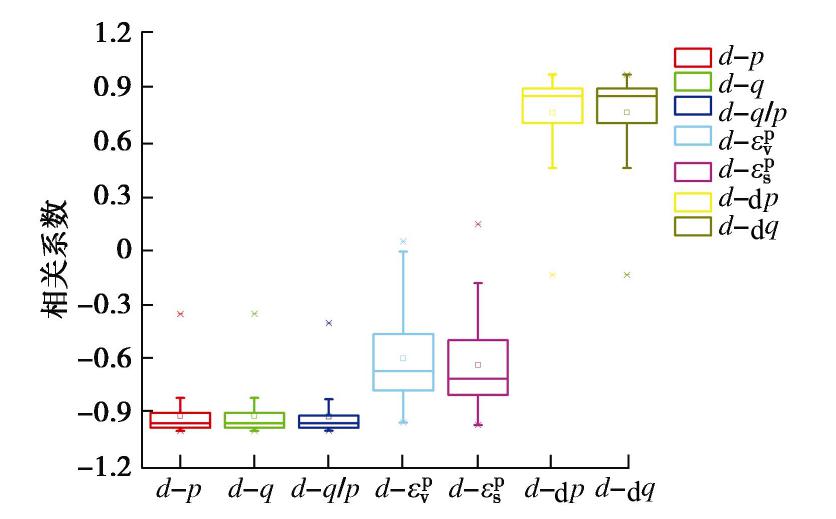
剪胀率$d$是评价土的剪胀性的重要指标,因此对剪胀率影响因素的研究显得尤为必要。对于剪胀型土,Roscoe等^[27]认为$d$与应力比$q/p$有关。Cubrinovski 等^[8]指出$d$会受到塑性剪应变${\epsilon }_{\text{s}}^{\text{p}}$的影响。考虑到塑性体应变${\epsilon }_{\text{v}}^{\text{p}}$也是描述土的剪胀性的一个重要参数,所以表明d与${\epsilon }_{\text{v}}^{\text{p}}$,${\epsilon }_{\text{s}}^{\text{p}}$均存在相关关系。岩土材料不同于其他材料,其变形过程不仅取决于当前应力状态,还与应力增量状态有关。综上分析,本文利用155个剪胀型土样本的剪胀性大数据,分别计算了$d$与应力、应变以及应力增量之间的相关系数,结果如图3所示。

图  3  剪胀率与不同影响因素之间的相关系数

Figure  3.  Correlation coefficient between dilatancy ratio and different influencing factors

下载: 全尺寸图片 幻灯片

从图3可知,$d$与$p$,$q$的相关系数均值约为-0.9,$d$与$q/p$的相关系数均值高达-0.92,表明$d$与$p,q,q\text{/}p$均为高度负相关；$d$与${\epsilon }_{\text{v}}^{\text{p}}$,${\epsilon }_{\text{s}}^{\text{p}}$的相关系数均值分别为-0.61,-0.65,表明$d$与${\epsilon }_{\text{v}}^{\text{p}}$,${\epsilon }_{\text{s}}^{\text{p}}$呈负相关；$d$与$\text{d}p,\text{d}q$的相关系数均值约为0.75,表明$d$与$\text{d}p$,$\text{d}q$呈正相关。考虑到$p,q,q\text{/}p$均为应力型影响因素,$p$和$q$ 又处于同一量级,$d$与$q/p$的相关性更强,且远高于${\epsilon }_{\text{v}}^{\text{p}}$,${\epsilon }_{\text{s}}^{\text{p}}$,$\text{d}p,\text{d}q$,所以在本文中选择$q/p$作为$d$的主要影响因素,而将${\epsilon }_{\text{v}}^{\text{p}}$,${\epsilon }_{\text{s}}^{\text{p}}$,$\text{d}p,\text{d}q$作为$d$的附加影响因素进行研究。

2.3   剪胀率与各影响因素之间的相关性函数

在本节中,基于剪胀型土的剪胀性大数据特征,根据其基本力学特性和本文提出的DLMR算法,分别建立了剪胀率与各影响因素之间的相关性函数。

（1）剪胀率与主要影响因素之间的相关性函数

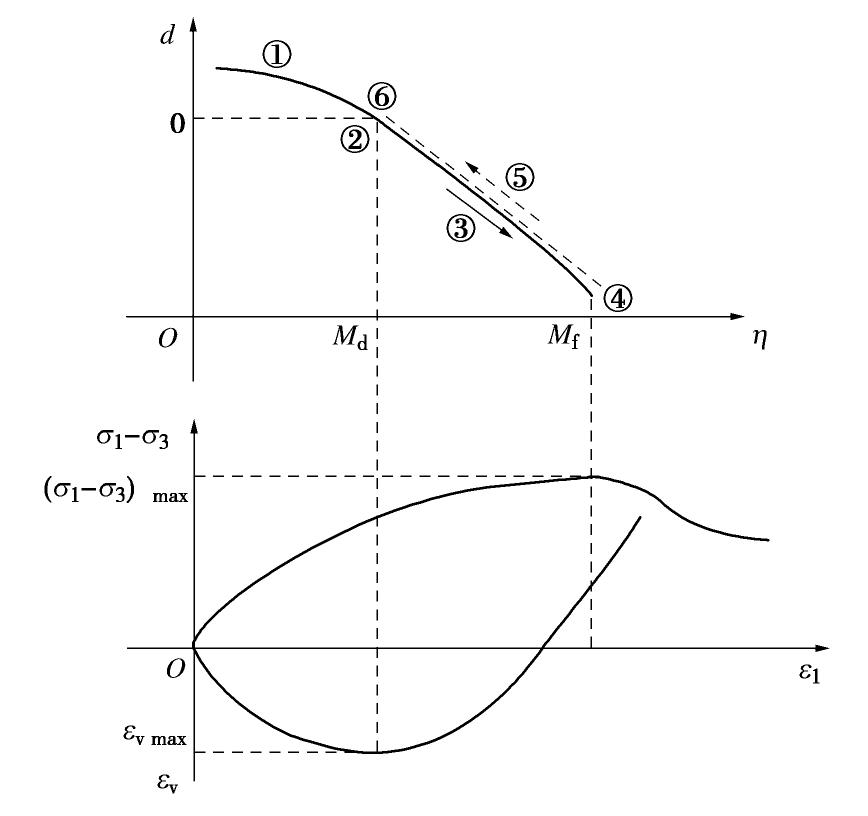
研究土的剪胀性的最佳方法是绘制$d$随应力比（$q/p$可记作$\eta$）变化的曲线。剪胀型土的变化过程如图4所示,可分为3个特征阶段和3个特征点。图中的$M_{\text{d}}$表示剪胀应力比,它与${\epsilon }_{\text{v}}-{\epsilon }_1$坐标系中的${\epsilon }_{\text{vmax}}$相对应,即表明土体在达到$M_{\text{d}}$之前,一直处于剪缩变形；当达到$M_{\text{d}}$时,体积压缩变形达到最大；经过$M_{\text{d}}$之后,土体开始膨胀变形,即$M_{\text{d}}$为土体由剪缩状态转换为剪胀状态的特征点。$M_{\text{f}}$则表示峰值应力比,它与$（{\sigma }_{\text{1}}-{\sigma }_{\text{3}}）-{\epsilon }_{\text{1}}$坐标系中的$（{\sigma }_{\text{1}}-{\sigma }_{\text{3}}{）}_{\max }$相对应,即土体所能达到的最大应力比。

图  4  剪胀型土的剪胀率随应力比的变化

Figure  4.  Change of dilatancy ratio with stress ratio of dilatant soil

下载: 全尺寸图片 幻灯片

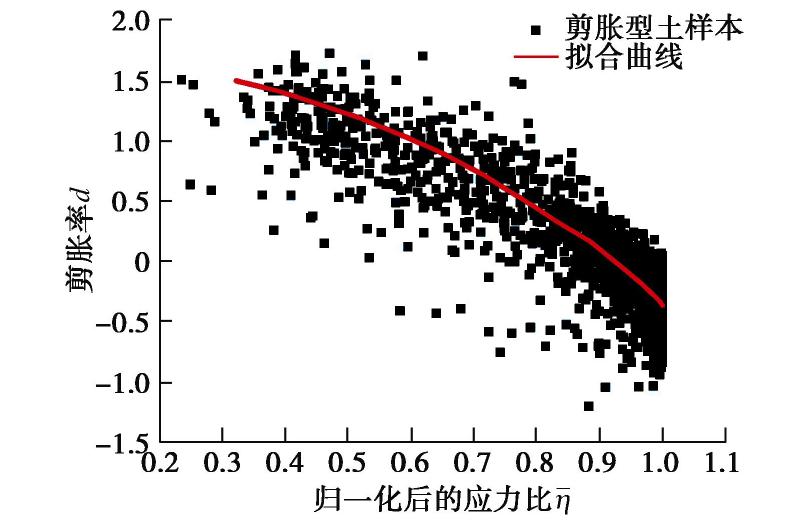
从图4可知：①剪缩阶段,此时$0<\eta <M_{\text{d}}$,$d>0$,土体为剪缩变形；②相变转换特征点,此时$\eta =M_{\text{d}}$,$d=0$；③剪胀阶段,此时$M_{\text{d}}<\eta <M_{\text{f}}$,$d<0$,土体为剪胀变形；④峰值应力比点,此时$\eta =M_{\text{f}}$,$d<0$,土体为剪胀变形；⑤软化阶段,此时$M_{\text{d}}<\eta <M_{\text{f}}$,$d<0$,土体为剪胀变形；⑥临界特征点,$d=0$。考虑到剪胀型土样本的$\eta$范围差别较大,所以基于峰值应力比$M_{\text{f}}$对$\eta$进行归一化处理,如下式：

$\overline{\eta }$表示归一化后的$\eta$,根据如图5所示的$d$与$\overline{\eta }$的大数据特征,再依据上述①～⑥的变形阶段,参考修正剑桥模型和统一硬化理论^[28],可提出相关性函数如下式：

图  5  $d$与$\overline{\eta }$的大数据特征

Figure  5.  Big data characteristics of $d$ and $\overline{\eta }$

下载: 全尺寸图片 幻灯片

式中,$d_{\eta }$表示主要影响因素$\eta$所对应的剪胀率,$\overline{M_{\text{d}}}$为$\overline{\eta }$所对应的剪胀应力比,$\overline{M_{\text{f}}}$为$\overline{\eta }$所对应的峰值应力比。通过本文提出的DLMR算法,即可得到如图5所示的拟合曲线。此时参数为：$n_1$=3.610,$n_2$=1.251,$n_3$=0.027,拟合度为0.764。

（2）剪胀率与附加影响因素之间的相关性函数

在上节中,已研究了$\eta$对$d$的影响,并得到了$d_{\eta }$与$\eta$的相关性函数。本节中利用式（5）即可得到附加因素${\epsilon }_{\text{v}}^{\text{p}},{\epsilon }_{\text{s}}^{\text{p}},\text{d}p,\text{d}q$对剪胀率的影响。

式中,$d_{\text{re}}$表示纯考虑应力比的剪胀率误差,也是附加影响因素对剪胀率影响的比例。本节主要研究$d_{\text{re}}$与附加影响因素之间的相关关系。

a）$d_{\text{re}}$与${\epsilon }_{\text{v}}^{\text{p}}$的相关性函数

考虑到剪胀型土样本的${\epsilon }_{\text{v}}^{\text{p}}$范围差别较大,本文将${\epsilon }_{\text{v}}^{\text{p}}$归一化后再进行研究,归一化方法如下式所示：

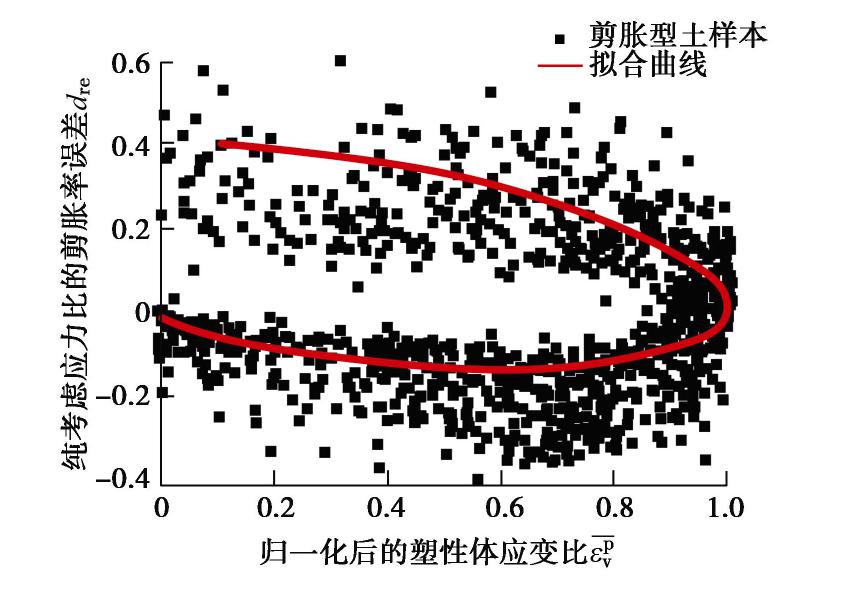
式中,${\epsilon }_{\text{v}}^{\text{p}}{}_{\text{cs}}$表示临界状态（critical state）时的${\epsilon }_{\text{v}}^{\text{p}}$,${\epsilon }_{\text{v}}^{\text{p}}{}_{\text{pts}}$表示相变转换状态（phase transformation state）时的${\epsilon }_{\text{v}}^{\text{p}}$,$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$表示归一化后的${\epsilon }_{\text{v}}^{\text{p}}$,$d_{\text{re}}$与$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$的大数据特征关系如图6所示。

图  6  $d_{\text{re}}$与$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$的大数据特征

Figure  6.  Big data characteristics of $d_{\text{re}}$ and $\overline{{\epsilon }_{\text{v}}^{\text{p}}}$

下载: 全尺寸图片 幻灯片

从图6可知,在剪缩阶段,$d_{\text{re}}$随着$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$的增大逐渐减小,达到相变特征状态时$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$达到最大,有$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$=1,$d_{\text{re}}$趋于0。在剪胀阶段,$d_{\text{re}}$随着$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$的减小而先减小后增大,达到临界状态时有$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$=0,$d_{\text{re}}$趋于0。由于$d_{\text{re}}$与$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$的特征关系可近似为椭圆曲线。因此可建立如下椭圆方程：

式中,$n_{\text{5}}$表示椭圆的长半轴长,$n_{\text{6}}$为短半轴长。$n_{\text{4}}$和$n_{\text{7}}$分别表示平移和旋转参数。同时,式（7）可表示为式（8）的形式,即为$d_{\text{re}}$与$\overline{{\epsilon }_{\text{v}}^{\text{p}}}$之间的相关性函数：

通过本文提出的DLMR算法,即可得到如图6中的拟合曲线,此时参数为$n_{\text{4}}$=0.437,$n_{\text{5}}$=0.425,$n_{\text{6}}$=0.241,$n_7$=0.183,拟合度为0.653。

b）$d_{\text{re}}$与${\epsilon }_{\text{s}}^{\text{p}}$的相关性函数

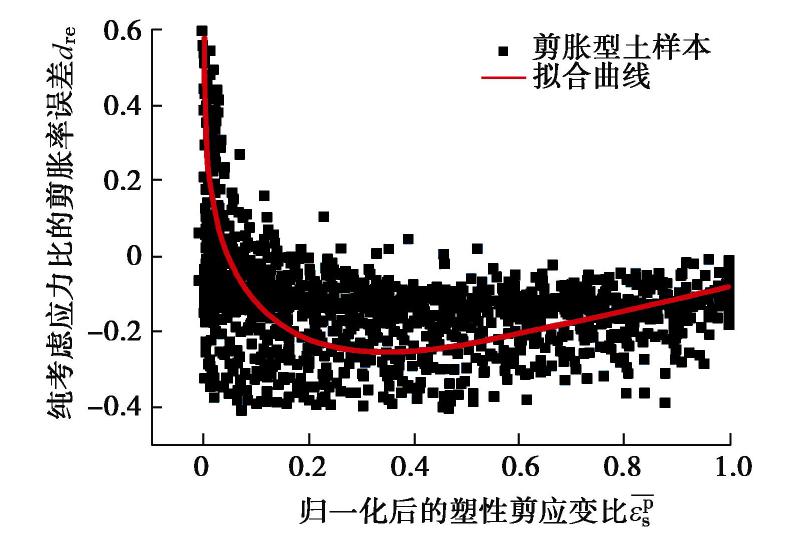
根据剪胀型土的基本力学特性可知,塑性剪应变${\epsilon }_{\text{s}}^{\text{p}}$在剪切作用下逐渐增大。考虑到${\epsilon }_{\text{s}}^{\text{p}}$在临界状态下仍然会继续增大,所以本文将初始临界状态（initial critical state）时的${\epsilon }_{\text{s}}^{\text{p}}$记作${\epsilon }_{\text{s}}^{\text{p}}{}_{\text{ics}}$。又因为剪胀型土样本的${\epsilon }_{\text{s}}^{\text{p}}$范围差别较大,因此基于${\epsilon }_{\text{s}}^{\text{p}}{}_{\text{ics}}$对${\epsilon }_{\text{s}}^{\text{p}}$进行归一化处理,$\overline{{\epsilon }_{\text{s}}^{\text{p}}}$表示归一化后的${\epsilon }_{\text{s}}^{\text{p}}$,如下式所示：

$d_{\text{re}}$与$\overline{{\epsilon }_{\text{s}}^{\text{p}}}$的大数据特征关系如图7所示。

图  7  $d_{\text{re}}$与$\overline{{\epsilon }_{\text{s}}^{\text{p}}}$的大数据特征

Figure  7.  Big data characteristics of $d_{\text{re}}$ and $\overline{{\epsilon }_{\text{s}}^{\text{p}}}$

下载: 全尺寸图片 幻灯片

从图7可知,在剪缩阶段,$d_{\text{re}}$随着$\overline{{\epsilon }_{\text{s}}^{\text{p}}}$的增大而减小；在剪胀阶段,$d_{\text{re}}$随着$\overline{{\epsilon }_{\text{s}}^{\text{p}}}$的增大先减小,再逐渐增大,因此可提出$d_{\text{re}}$与${\epsilon }_{\text{s}}^{\text{p}}$的相关性函数如下式所示：

通过本文提出的DLMR算法,即可得到如图7中所示的拟合曲线。此时参数为：$n_{\text{8}}$=-0.701,$n_{\text{9}}$=0.232,$n_{\text{10}}$=-0.137,拟合度为0.668。

c）$d_{\text{re}}$与$\text{d}p$,$\text{d}q$的相关性函数

考虑到剪胀型土样本中$\text{d}p$和$\text{d}q$范围差别较大,因此选择先期固结压力$p_{\text{c}}$分别对其进行归一化处理,如下式所示：

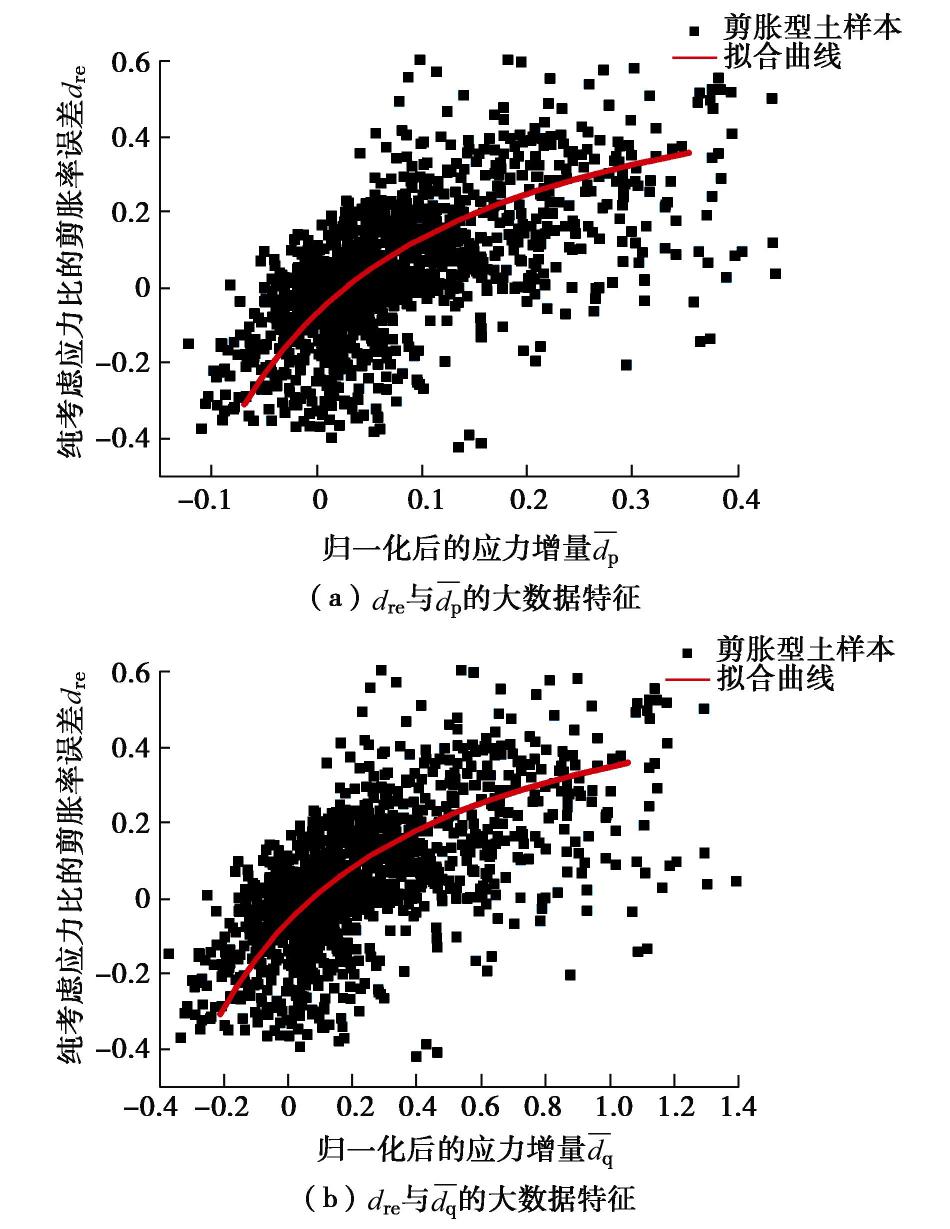
式中,$\overline{\text{d}p}$和$\overline{\text{d}q}$分别表示归一化后的$\text{d}p$和$\text{d}q$。$d_{\text{re}}$与$\overline{\text{d}p}$,$\overline{\text{d}q}$的大数据特征关系如图8（a）,（b）所示。

图  8  $d_{\text{re}}$与应力增量的大数据特征

Figure  8.  Big data characteristics of $d_{\text{re}}$ and stress increment

下载: 全尺寸图片 幻灯片

从图8（a）,（b）可知,$d_{\text{re}}$分别随着$\overline{\text{d}p}$,$\overline{\text{d}q}$的增加而逐渐变大,因此可提出$d_{\text{re}}$分别与$\text{d}p$,$\text{d}q$的相关性函数如下式所示：

通过本文提出的DLMR算法,即可得到如图8（a）,（b）中所示的拟合曲线。此时式（13）中参数为$n_{\text{11}}$=-0.028,$n_{\text{12}}$=0.671,$n_{\text{13}}$=1.353,拟合度为0.635。此时式（14）中参数为：$n_{\text{14}}$=-0.075,$n_{\text{15}}$=1.238,$n_{\text{16}}$=1.431,拟合度为0.638。

2.4   剪胀型土的剪胀模型

从2.3节的结论可知,基于大量剪胀型土样本试验数据建立的剪胀率与各影响因素之间的相关性函数拟合度均较低,这表明了剪胀率不能只考虑单一因素的影响,而是需要综合考虑主要因素和附加因素的影响。$d_{\text{re}}$与${\epsilon }_{\text{v}}^{\text{p}},{\epsilon }_s^p,\text{d}p,\text{d}q$之间的相关性函数实际上包含了所有附加影响因素的影响,因此在总的剪胀计算模型中需要根据它们的相关性差异进行加权处理。

本文计算了$d_{\text{re}}$与各附加影响因素之间的相关系数,如表4所示,其中$r_{{\epsilon }_{\text{v}}^{\text{p}}}$,$r_{{\epsilon }_{\text{v}}^{\text{p}}}$,$r_{\text{d}p}$,$r_{\text{d}q}$分别表示$d_{\text{re}}$与${\epsilon }_{\text{v}}^{\text{p}},{\epsilon }_{\text{s}}^{\text{p}},\text{d}p,\text{d}q$之间的相关系数。

表  4  $d_{\text{re}}$与各附加影响因素之间的相关系数

Table  4.  Correlation coefficient between $d_{\text{re}}$ and additional factors

$r_{{\epsilon }_{\text{v}}^{\text{p}}}$	$r_{{\epsilon }_{\text{s}}^{\text{p}}}$	$r_{\text{d}p}$	$r_{\text{d}q}$
-0.65	-0.69	0.63	0.63

下载: 导出CSV 

| 显示表格

由此可计算出各附加因素对$d_{\text{re}}$影响的权重值,如下式所示：

式中,$w_{{\epsilon }_{\text{v}}^{\text{p}}}$表示${\epsilon }_{\text{v}}^{\text{p}}$对$d_{\text{re}}$的影响权重值。同理可求得$w_{{\epsilon }_{\text{s}}^{\text{p}}}$=0.266,$w_{\text{d}p}$=0.242,$w_{\text{d}q}$=0.242。

综上,本文根据剪胀型土的基本力学特性,结合主要影响因素和附加影响因素的相关性函数,综合建立了如下式所示的剪胀模型：

式中,$f(\eta )$表示主要影响因素$\eta$与$d_{\eta }$的相关性函数；$f_1({\epsilon }_{\text{v}}^{\text{p}})$,$f_2({\epsilon }_{\text{s}}^{\text{p}})$,$f_3(\text{d}p)$,$f_4(\text{d}q)$分别表示附加影响因素${\epsilon }_{\text{v}}^{\text{p}},{\epsilon }_{\text{s}}^{\text{p}},\text{d}p,\text{d}q$与$d_{re}$的相关性函数。同时,式（16）可转换为式（5）的形式,即$d=d_{\eta }(1+d_{\text{re}})$。本文剪胀模型中的各参数值分别从2.3节建立的各相关性函数中通过DLMR算法获得,如表5所示。

表  5  剪胀模型的参数值

Table  5.  Parameter values of dilatancy model

主要影响因素参数			附加影响因素参数
$n_1$	$n_2$	$n_3$	$n_{\text{4}}$	$n_{\text{5}}$	$n_{\text{6}}$	$n_7$	$n_8$	$n_9$	$n_{10}$	$n_{11}$	$n_{\text{12}}$	$n_{\text{13}}$	$n_{\text{14}}$	$n_{15}$	$n_{16}$
3.610	1.251	0.027	0.437	0.425	0.241	0.183	-0.701	0.232	-0.137	-0.028	0.671	1.353	-0.075	1.238	1.431

下载: 导出CSV 

| 显示表格

从式（16）可知,当土处于相变特征状态时,本文模型有$f(\eta )$=0,从而有$d$=0；当处于临界状态时,本文模型有$f(\eta )$=0,同样可得到$d$=0。此外,本文模型与剪胀型土样本所有试验数据的剪胀率拟合度为0.932,明显高于各类影响因素的相关性函数拟合度。综上分析,结果表明了本文模型不仅能够良好的模拟剪胀型土的剪胀率变化的共同规律,同时也进一步证明了考虑主要因素和附加因素综合影响的剪胀模型是更为科学合理的。

3.   模型的检验

3.1   模型的比较

目前,应用广泛的剪胀模型主要有修正剑桥模型下剪胀模型的改进式,如式（17）所示,本文中记作模型1；Rowe模型,如式（18）所示,本文中记作模型2。

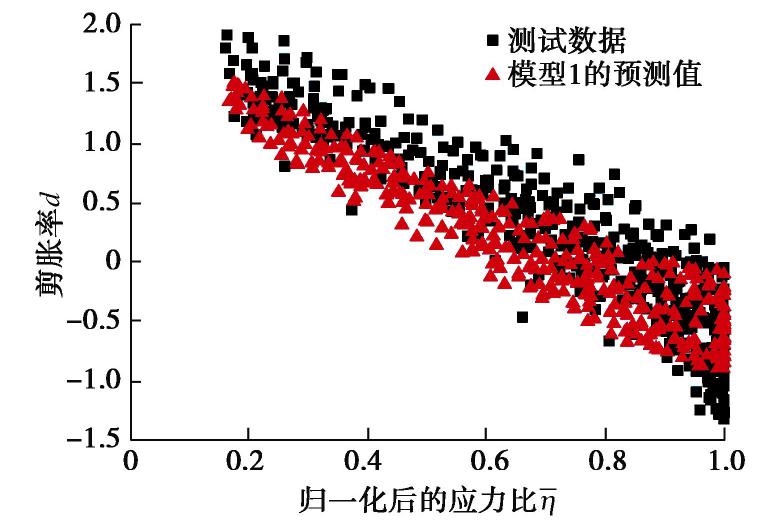
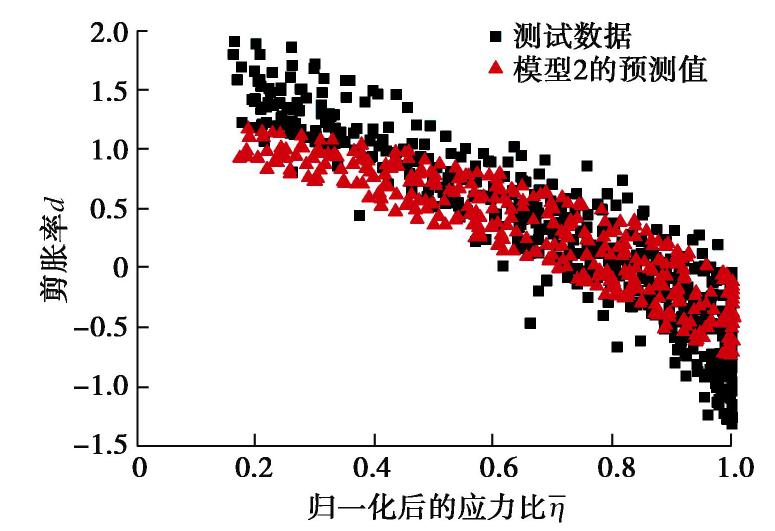
式中,$R$为大小主应力比,$R_{\text{u}}$为极限主应力比。模型1是姚仰平等^[29]针对修正剑桥模型,利用剪胀应力比$M_{\text{d}}$替换$M$得到。SHIVEL^[30]利用式（17）建立了本构模型,并取得了一定的研究成果。模型2是由Rowe建立的剪胀模型,可较好的描述砂土的剪胀特性。本文提出的剪胀模型是在大量剪胀性试验数据的分析处理基础上,再根据其基本力学特性和DLMR算法建立的,所以它不同于一般统计学意义上的计算模型,而是具有一定理论意义和应用背景的计算模型。为了验证本文模型的适用性和准确性,重新选择了一组未参与之前模型建立的试验数据作为测试数据。一般地,用于建立模型的训练数据（155个剪胀型土样本）和测试数据的数量之比为7∶3,所以测试数据包含了66个新的剪胀型土样本。作为测试数据的剪胀型土样本同样也来源于表2中的期刊文献资料,并且测试数据的选择标准和过程也与训练数据组相同。因此利用测试数据分别在模型1,模型2以及本文模型下进行比较,结果如图9～11所示。

图  9  模型1的剪胀率预测值

Figure  9.  Predicted values of dilatancy ratio of model 1

下载: 全尺寸图片 幻灯片

图  10  模型2的剪胀率预测值

Figure  10.  Predicted values of dilatancy ratio of model 2

下载: 全尺寸图片 幻灯片

图  11  本文模型下的剪胀率预测值

Figure  11.  Predicted value of dilatancy ratio of proposed model

下载: 全尺寸图片 幻灯片

在图9中,模型1与测试数据的剪胀率拟合度为0.665。虽然模型1在修正剑桥模型的基础上,引入了剪胀应力比$M_{\text{d}}$,使其能大致描述剪胀型土的剪胀变化过程,但通过模型1计算得到的剪胀率在其剪缩阶段数值偏小,表明模型1低估了其剪缩性,而在剪胀阶段数值偏大,表明模型1高估了其剪胀性。

在图10中,模型2与测试数据的剪胀率拟合度为0.605。相较于模型1,模型效果有所降低,这是由于模型2在描述粗粒土的剪胀特性时,会过大地估计其剪胀变形。

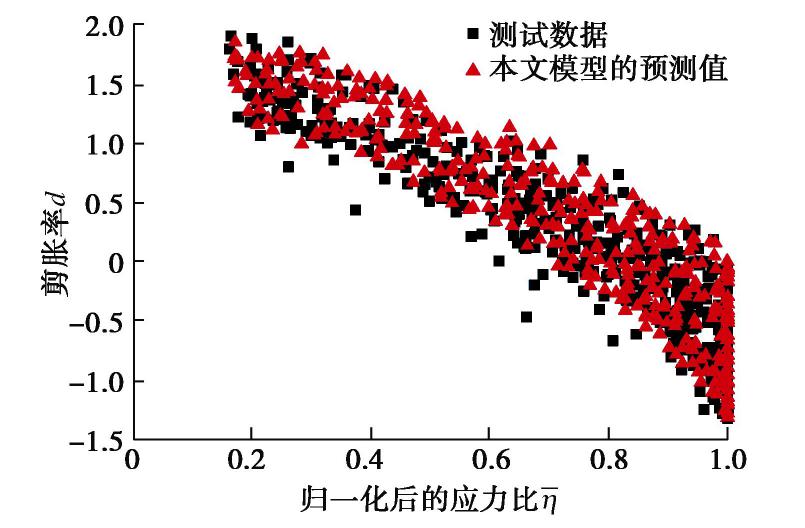
在图11中,本文模型（见式（16）和表5）与测试数据组的剪胀率拟合度为0.934。相较于模型1和模型2,其模型效果明显提高。笔者认为主要原因是本文模型考虑了剪胀率的主要因素和附加因素的综合影响,因此解决了模型1和模型2在剪缩阶段剪缩性被低估,在剪胀阶段剪胀性被高估的问题。

综上分析,本文模型可良好的描述剪胀型土的剪胀变化特性,这也是本文在剪胀型土的剪胀性大数据基础上进行特征深度挖掘与研究的原因所在。

3.2   模型的验证

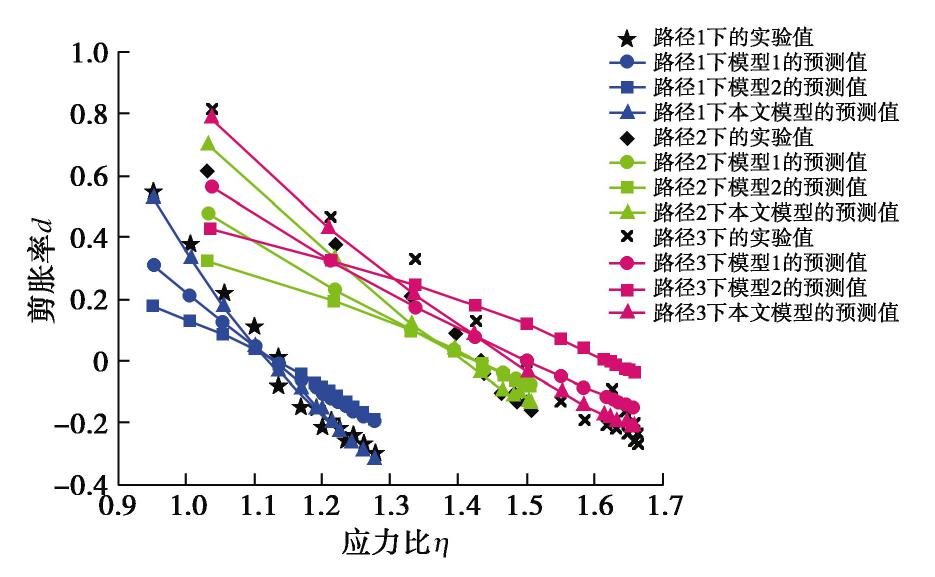
为了验证本文模型的适用性,选择了未参与本文统计的文献[31～33]中样3种不同应力路径下的试验数据。不同应力路径下3种剪胀模型的预测效果如图12所示。

图  12  不同应力路径下3种剪胀模型的拟合效果图

Figure  12.  Fitting effects of three models for dilatancy ratio under different stress paths

下载: 全尺寸图片 幻灯片

从图12和表6可知,模型1和模型2虽然可以大致描述剪胀率变化的情况,但在剪缩阶段,两种模型都低估了其剪缩性,而在剪胀阶段,两种模型均高估了其剪胀性。此外,模型1和模型2的预测值与试验值之间的欧氏距离较大,说明预测值与试验值误差较大。本文模型（式（16）和表5）计算的欧式距离基本保持在相对较小的范围内,说明本文模型与试验值误差较小。总的来说,本文模型不仅能够良好的描述各阶段和特征状态下的剪胀率变化情况,而且在不同应力路径下对于剪胀型土的剪胀变化特性均有较强地适应性。

表  6  不同应力路径下的3种模型预测与试验值的欧式距离

Table  6.  Euclidean distances of predicted values and experimental data of three models under different stress paths

类型	路径1	路径2	路径3
本文模型	0.131	0.153	0.191
模型1	0.423	0.336	0.412
模型2	0.581	0.424	0.721

下载: 导出CSV 

| 显示表格

为了量化不同应力路径下剪胀模型的拟合效果,试验值与3种剪胀模型的预测值之间的欧氏距离如表6所示。

4.   讨论

本文利用大数据深度挖掘技术,得到了剪胀型土的剪胀性大数据特征,并建立了剪胀率与各影响因素的相关性函数。在此基础上,构建了新的剪胀模型。

（1）在一般剪胀性的计算模型中,认为应力比是剪胀率的唯一影响因素。本文通过对大量剪胀型土剪胀性试验数据的特征挖掘,发现剪胀率不仅与应力有关,还与应变和应力增量有关,这就是一般剪胀模型不合理的根本原因。由各相关性函数综合建立的剪胀模型的拟合度明显高于单个影响因素的拟合度,进一步表明了剪胀型土的剪胀率仅仅考虑单个因素的影响是远远不够的,必须考虑主要因素和附加因素的综合影响。

（2）利用大数据技术研究土的剪胀特性是课题组在土的本构关系与大数据的交叉领域中初步的探索。希望能从中获取关于剪胀性的变化规律,加深对土体基本力学特性的认识。本文提出的剪胀模型较合理地考虑了剪胀率各类影响因素的综合影响,下一步还需要探索模型中拟合参数的物理意义。

5.   结论

（1）提出了一种基于Hadoop+Spark的分布式DLMR回归算法。该算法结合了LM算法,并在Spark分布式框架下解决了大量剪胀型土的剪胀性试验数据回归分析时的全局优化性差、收敛性慢、计算不稳定的问题。

（2）通过大数据深度挖掘技术,揭示了应力、应变以及应力增量对剪胀型土的剪胀性影响的大数据特征。通过本文提出的DLMR算法分别得到了剪胀率与各影响因素之间的相关性函数。根据剪胀型土的基本力学特性,建立了可以反映其剪胀特性共同规律的剪胀模型。

（3）本文模型和剪胀型土样本所有试验数据的剪胀率拟合度为0.932,明显优于修正剑桥模型下剪胀模型的改进式和Rowe模型,并且还可以较好地反映不同应力路径下本文未统计的试验样本的剪胀特性。