DEM simulation of instability mode in sand under constant shear drained conditions
-
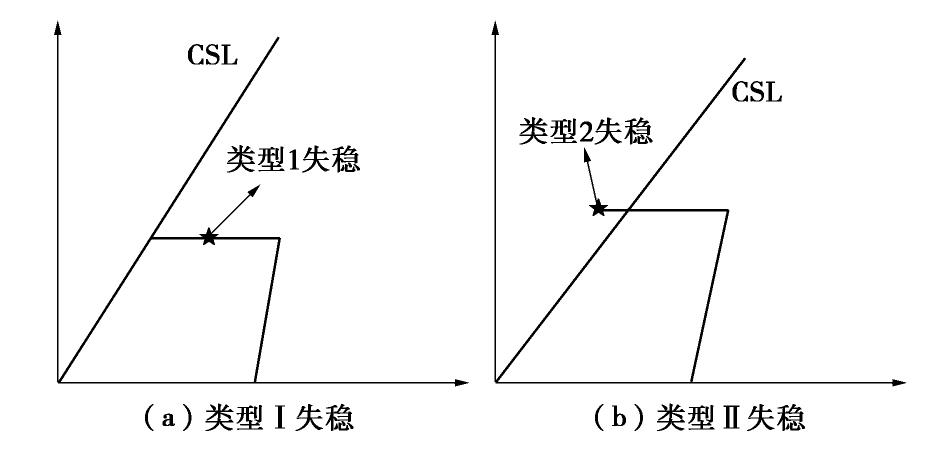
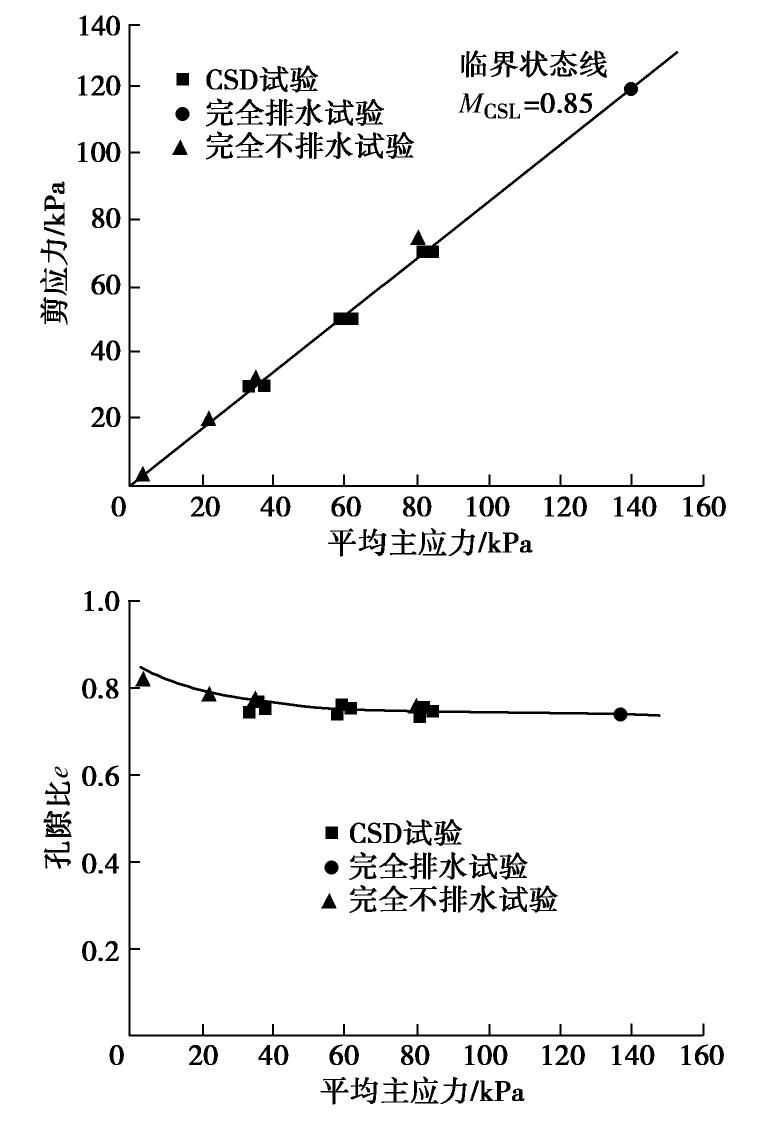
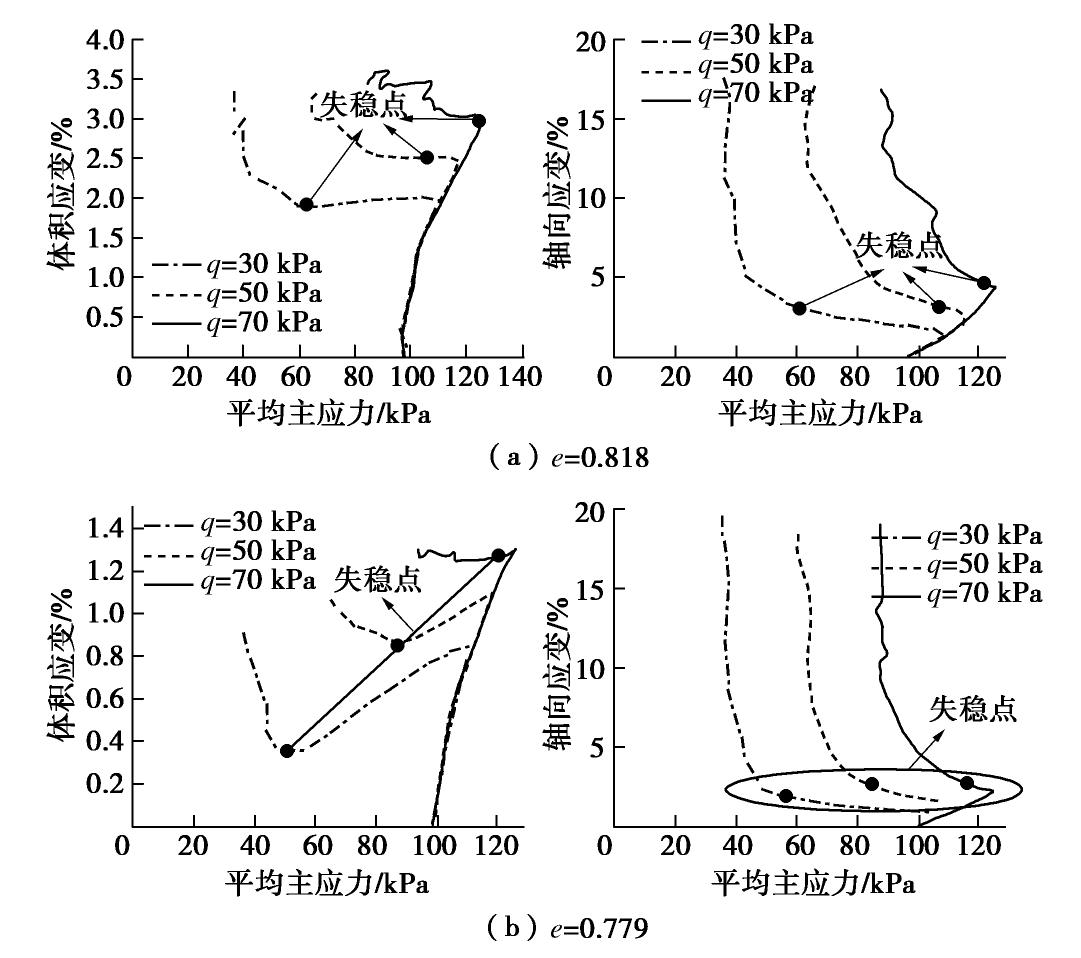
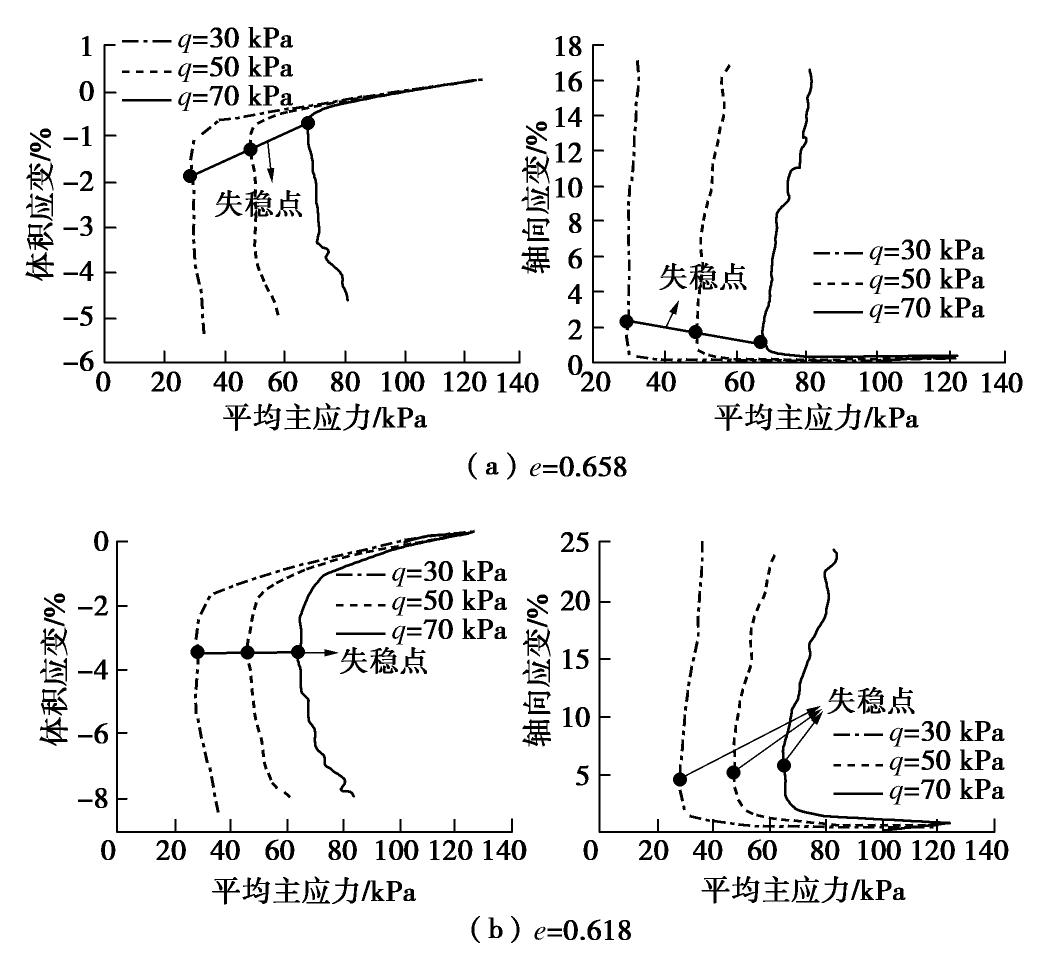
摘要: 松砂在不排水条件下会发生分散性的液化失稳,失稳点在破坏线内。近年来的研究表明,砂土在完全排水条件下也会发生分散性失稳,可用常偏应力剪切(CSD)试验来研究。在CSD试验中,控制偏应力的误差是得出正确结果的关键。采用离散元数值方法模拟了砂土试样在不同剪应力水平下的CSD试验,实现了偏应力的较精准控制。根据模拟结果,采用Hill的二阶功准则,结合失稳时的应力与变形特征,详细分析了CSD试验中发生的Ⅰ型和Ⅱ型两种失稳模式,讨论了在CSD加载路径下初始孔隙比和剪应力水平对砂土失稳的影响。模拟结果表明,松散试样发生了Ⅰ型失稳,而密实试样发生了Ⅱ型失稳,且初始孔隙比越大越易失稳;剪应力水平越高,失稳发生的越快。结合三轴不排水和排水剪切模拟结果,讨论了失稳线(IL)斜率与初始孔隙比之间的关系,并将模拟结果与室内多种砂的试验结果进行了比较分析,进一步提出了砂土失稳的排水与不排水统一分析方法。Abstract: Loose sandy soil can undergo static liquefaction under undrained conditions and the onset of instability is within the failure line, and this kind of instability is called diffusion instability. In recent years, some studies have shown that failure can occur under drained conditions. The constant shear drained (CSD) tests can be performed to investigate this drained instability. A key point of CSD tests is to control the error of deviating stress for getting reliable results in experiments. The discrete element method is used to simulate the CSD tests of sand with different densities under different shear stress levels. Based on the Hill's second-order work criterion, the possible model for instability in CSD tests are divided into two types. Both the modes of instability are observed in DEM simulations. The influences of initial void ratio and shear stress level are analyzed on instability under CSD loading path. The numerical results indicate that the samples with lager void ratio are easy to collapse, and the higher the shear stress level, the faster the instability occurs. The slope of instability line (IL) associated with the initial void ratio is also discussed in details, and a unified method is proposed to analyze sand instabilities under both drained and undrained stress paths. Finally, the numerical results from this study are compared with test ones of several kinds of sands.
-
Keywords:
- sand /
- instability /
- discrete element method /
- constant shear drained test /
- second-order work
-
0. 引言
黄土作为风成土具有较强的结构性,结构性土具有较高的抗压和抗剪能力。但这种结构性在浸水或者扰动作用下会发生破坏,进而导致土的力学性质发生显著变化,如湿陷性、承载力降低和强度弱化等现象[1-2]。原状黄土经过开挖、击实等扰动后,其粒间架空孔隙结构发生破坏,孔隙被压缩,变为重塑黄土,此时原状黄土的湿陷性丧失,进而成为路用性能较好的填筑材料。随着一带一路倡议的推进,一大批交通基础设施工程建设于黄土地区,交通荷载引起了黄土地基严重的永久变形,如兰新高铁黄土地基产生了较大工后不均匀沉降(最大沉降62 mm)[3],西宝高速公路、通黄高速公路、连云港—兰州铁路等黄土地基也出现了较大的工后不均匀沉降[4]。因此,研究循环交通荷载作用下的重塑黄土的力学性质具有重要的现实意义。
岩土工程领域内的实际工程建设经常会发生主应力轴旋转现象,尤其是在边坡、土方开挖及路基填筑等工程问题中[5]。此外,在地震、波浪、尤其是车辆交通荷载等循环荷载作用下,地基土中的应力路径发生变化。以交通荷载为例,其应力特征为主应力方向连续旋转与剪应力幅值耦合变化的心形线应力路径,车轮正下方的土体单元的主应力在-90°~90°间做连续变化,如图 1所示。其中主应力轴旋转不仅产生弹性变形,也会产生部分塑性变形,这已成为业内共识[6-7]。
目前,国内外针对于主应力旋转的研究主要集中在砂土和软黏土方面[8-10]。沈扬等[11]依托浙江大学HCA较早地针对原状软黏土进行了一系列的主应力轴旋转试验,发现主应力轴旋转对土体孔压的积累带来显著的影响。王钰轲等[12]对饱和软黏土开展了主应力轴连续旋转试验,指出随着孔压的增加,竖向模量和剪切模量均随着循环应力比和围压的增加逐渐降低。刘家顺等[13]通过对软黏土的孔压和塑性应变的累积进行分析,得到累积塑性应变随循环剪应力比和循环动应力比的增大而增大的变化规律。扈萍等[14]对粉细砂的非共轴变形进行了细致研究,发现中主应力系数和循环起始角度对粉细砂竖向应变、剪切应变及体应变等有明显影响。Prasanna等[15]通过空心圆柱扭剪试验对砂土液化的敏感性进行了分析,结果表明液化敏感性增加可能是由于最大剪应力平面与层面的倾角等因素造成的。
黄土作为良好的路基填筑材料,在西北地区道路工程建设中起到重要作用。而目前针对于黄土路基在交通荷载作用下的研究较少。为此,本文以重塑黄土作为研究对象,借助空心圆柱扭剪仪对饱和重塑黄土在主应力轴旋转下的变形特性展开研究,以期为实际工程中黄土路基的变形控制提供科学依据。
1. 试验基本情况
试验仪器为长安大学GDS空心圆柱扭剪仪(图 2),该仪器主要包括围压控制系统和外力控制系统。仪器可以对试样施加独立控制的外压(Po)、内压(Pi)、轴力W和扭矩MT,从而实现主应力轴连续旋转等复杂条件下的试验应力路径。关于仪器的具体描述参见Yang等[16]的研究。
试验所用土样为重塑黄土,土样的基本物理性质指标见表 1。将原状黄土烘干、粉碎后按照一定的含水率拌合,密封至保鲜袋中18~24 h,确保含水率均匀,后将土料分层放入安装好的模具内,每装入100 g击实一次,最终制备完成试样[17]。试样尺寸为高度×外径×内径=200 mm×100 mm×60 mm。采用空心圆柱扭剪仪对制备好的土样进行反压饱和(反压分别为50,100和150 kPa;围压分别为70,120和170 kPa),采用三级饱和法,直至孔压系数B≥0.96[18],即可认为土样达到饱和状态,随后进行等压固结,保持反压不变,同时将内压和外压增大至250 kPa,最终完成土样的固结。
表 1 土样物理指标Table 1. Physical parameters of soil samples含水率
/%密度
/(g·cm-3)干密度
/(g·cm-3)相对质量密度 液限
/%塑限
/%14.2 2.07 1.83 2.71 13.8 18.9 交通荷载作用引起地基土单元体主应力轴发生连续循环旋转,其应力路径可简化为心形,因此,本试验采用动态加载模块,对土样施加不同循环荷载从而模拟路基上方交通荷载作用。具体地,开展了不同条件下饱和重塑黄土的循环三轴试验和循环交通荷载试验。在循环三轴试验中忽略埋深对路基土体单元的影响,引入了竖向循环应力比CVSR:
CVSR=σamplz/2p′0, (1) 式中,σamplz为循环动应力幅值,p′0为初始有效平均应力。在循环交通荷载试验中,忽略轴载的影响,引入了循环扭剪应力比η:
η=τamplzθ/σamplz, (2) 式中,τamplzθ为循环剪应力幅值。循环三轴试验仅从竖向循环动应力σcycz的角度出发,反映了其对路基沉降的影响,而循环交通荷载试验则反映了竖向循环动应力σcycz及循环剪应力τcyczθ两方面对路基沉降的影响。为了实现心形加载路径,引用心形线的参数方程:
X=a[2cos(t)−cos(2t)] ,Y=a[2sin(t)−sin(2t)] 。} (3) 根据试验方案对其进行适当的平移变化,就可得到本文所需的加载波形,如图 3所示,其中ω为加载频率,T为加载时间。
试验划分为12组,根据试验影响因素的不同,试验方案可分为2个系列,分别为循环三轴试验(η=0)和循环交通荷载试验(η≠0)。所有试样的有效固结压力σ3均为150 kPa,根据ASTM规范[19]选取试验加载频率为2 Hz(车辆速度约70 km/h),循环次数达10000次后停止试验。具体试验方案见表 2。
表 2 试验方案Table 2. Test programs系列编号 试样编号 σamplz
/kPaCVSR τamplzθ
/kPaη Ⅰ A1 20 0.10 0 0 A2 30 0.15 0 0 A3 40 0.20 0 0 Ⅱ B1 20 0.10 4 0.2 B2 20 0.10 6 0.3 B3 20 0.10 8 0.4 C1 30 0.15 6 0.2 C2 30 0.15 9 0.3 C3 30 0.15 12 0.4 D1 40 0.20 8 0.2 D2 40 0.20 12 0.3 D3 40 0.20 16 0.4 值得注意的是,对于渗透性较低的土类,绝大部分学者开展的循环加载试验均是在不排水条件下进行的,原因是一般加载频率范围内排水条件下的循环加载试验无法保证试样中孔压的完全消散,这样会造成试样内部孔压和有效应力分布不均匀,因而一般来说排水条件下的循环加载试验不能看作为标准的单元体试验。这样的单元体试验结果是不能直接用于本构模型验证的。实际工程的排水条件可以结合有效应力模型通过边值问题进行求解,而排水条件下的循环加载单元体试验结果可以作为边值问题的一种验证。因此,从工程实用角度来说,排水条件下的循环加载试验具有一定参考价值。基于上述原因本文开展的试验均在排水条件下进行。
2. 试验结果与分析
2.1 竖向塑性累积应变分析
图 4为竖向塑性累积应变εpz随竖向循环应力比CVSR变化图。从图 4中可以看出,两类试验中εpz均呈现出随循环次数的增大而增大的变化规律。在循环次数较低时,εpz增长速率很快,在N达到1000次后,εpz增长逐渐变缓,之后随循环次数的增长表现出缓慢增长的趋势,并最终逐渐趋于平稳。这主要是由于试验初始阶段试样孔隙结构逐渐被压密,当孔隙结构被压实至一定程度,累积应变也逐渐趋于稳定。当循环扭剪应力比η一定时,εpz随竖向循环应力比CVSR的增加而增加。而对比不同η下,同一循环次数下(图 4(e),以N=6000为例)的累积应变增长速率可发现,循环三轴试验中εpz随CVSR的增大速率接近于线性,而循环交通荷载试验呈现出非线性增长的趋势,这表明循环交通荷载对土体的竖向变形有着显著的影响。其原因在于即使仅有主应力轴方向的循环变化,土体也会产生相应的累积应变。此外,εpz随循环次数N的变化趋势与应力主轴是否发生旋转无关,其主要原因可能是土样压实度的影响。
图 5为竖向塑性累积应变εpz随循环扭剪应力比η的变化图。对比不同循环扭剪应力比η试验结果,可发现应力主轴的旋转会加速产生相应的竖向塑性累积应变。例如当N=10000,CVSR=0.2时,循环三轴试验的εpz为0.0442,循环交通荷载试验下,η=0.2,0.3和0.4时,εpz分别为0.0593,0.0813和0.1437,为循环三轴试验的1.34倍,1.84倍和3.25倍。此外,结合图 4和图 5,可发现循环竖向应力比和循环扭剪应力比的增加均会引起竖向塑性累积应变的增加,且当循环次数达到一定时(N≥1000),εpz逐渐趋于稳定。
2.2 径向与环向塑性累积应变分析
为反映不同循环应力比下,径向塑性累积应变随循环加载次数的变化规律,本文以η=0.3和CVSR= 0.15为例进行分析。图 6为径向塑性累积应变εpr随不同循环应力比的变化规律。由于等压固结时可能已产生部分径向应变,在此均取起始径向应变为参考点进行分析。从图 6中可以看出,径向塑性累积应变方向为负,说明起始径向受力状态为拉应力作用,在拉应力作用下试样短时间内产生很大的εpr,随着循环次数的增加,在达到某一值后,εpr开始反向不断累积。在η一定时,随着CVSR的增大,εpr产生的径向拉应变逐渐增大,同时,在CVSR一定时,不同η下,径向累积应变随循环次数的变化规律总体呈现出类似于不同CVSR下径向累积应变随循环次数的变化规律,即呈现出先快速降低后缓慢上升趋势。由此可推断出,加载初期试样受径向拉应力影响,快速发生变形,随循环次数的增加,εpr的增加速率逐渐减小,当达到一定循环次数时,径向应变达到了最大值,此时竖向循环应力产生的拉应力与循环扭剪应力产生的压应力相等,随后继续加载时,径向拉应力小于径向压应力,从而试样径向累积应变趋于减小。
在本文的试验过程中,内外围压在数值上始终相等,此时根据Hight等[20]提出的薄壁试样计算公式可知,环向应力和径向应力数值相等(σr=σθ),因此径向塑性累积应变σpr和环向塑性累积应变σpθ也应近似相等。为验证上述猜测,以η=0.3时环向塑性累积应变随不同竖向循环应力比的变化规律(如图 7所示)为例进行试验验证。对比图 7与图 6(a)可知,在相同应力比条件下,σpr和σpθ在数值上近似相等。这与Cai等[21]对砂土进行的围压恒定的定向剪切试验得到的结论相似。
2.3 累积塑性体应变分析
图 8为累积塑性体应变εpv随循环扭剪应力比η的变化图。由图 8可知,在循环次数较低时,εpv为负值,在循环次数达到某一值后,εpv开始逐渐由负转正,呈现出随循环次数的增大而增大的变化规律。在试验过程中,试样在扭矩MT作用下径向和环向上发生剪缩现象,而在轴力W作用下径向和环向上会发生剪胀现象,竖向呈现剪缩现象。试样的体应变计算公式如下所示:
εv=εz+εr+εθ, (4) 在循环次数较低时,扭剪次数较低,试样在径向和环向上的变形主要受轴力作用影响,试样在径向和环向上所受的拉应力大于竖向所受的压应力,试样整体受拉,体应变为负值。随着循环次数的增加,试样在循环扭剪应力的作用下,试样在径向和环向上出现径缩,试样整体受压,体应变为正值。同时由2.1节可知,主应力轴连续旋转会加速竖向应变的累积,因此随着循环次数的增加,试样体应变逐渐增大,出现由负转正的变化规律。
2.4 八面体塑性累积剪应变分析
图 9反映了八面体应变空间下,剪应变随循环扭剪比η变化规律。由图 9可知,γpoct随循环次数的增大而增大,且表现为对数型的增长态势。从图 9中可以看出,循环三轴试验和循环扭剪试验均呈现出随循环次数的增大而增大的变化规律。同时,随着η的增大,γpoct也相应增大。例如当CVSR=0.2时,试验结束时,循环三轴试验γpoct为0.128%,η=0.2,0.3和0.4时,γpoct分别为0.137%,0.174%和0.208%,分别是同条件下循环三轴试验的1.07倍,1.36倍,1.63倍。这说明应力主轴的旋转会加速八面体剪应变的累积,随着η的增大,土样的γpoct也增大。对比分析图 9,可发现在η不变时,γpoct随CVSR增大也出现相应的增大,但当η达到某一值(文中为η=0.4)且循环次数较大时,试样CVSR的增加不会引起γpoct发生明显变化。这表明η较大时,γpoct的收敛主要是由于循环扭剪应力所产生的,而不依赖于竖向循环应力比CVSR。
2.5 塑性累积应变对比分析
由于环向塑性累积应变与径向塑性累积应变数值近似相等,竖向塑性累积应变与累积塑性体应变变化规律也大体相似,在相同应力条件下,本文仅对竖向塑性累积应变、径向塑性累积应变和八面体塑性累积剪应变的发展规律进行对比,以加载结束时(N=10000次)的累积应变作为数据来源,对CVSR=0.15和η=0.3时3种应变形式进行了分析对比,如图 10所示。从结果看,对竖向累积应变和八面体累积应变而言,应变终值与循环扭剪应力比η和循环竖向应力比CVSR均呈正相关。且随不同应力比的增长趋势基本一致。但当CVSR一定时,径向累积应变终值随η增大在0.3处波动,可认为其和扭剪应力比的相关性不显著;当η一定时,径向累积应变终值随CVSR增大而逐渐减小,因此,可认为其和竖向循环应力比呈负相关。此外,循环交通荷载试验(η≠0)中累积变形大于循环三轴试验(η=0)累积变形,其中竖向塑性累积应变>八面体塑性累积应变>径向塑性累积应变,试验结果进一步表明了主应力轴旋转对路基稳定性有着显著的影响。
2.6 土类对比分析
前文已对循环交通荷载作用下饱和重塑黄土的变形特性进行了详细的分析,为更好地反映重塑黄土在实际工程中的应用价值,将本文试验结果与郭林[22]的饱和原状软黏土试验结果进行比较。图 11为相同CVSR和η情况下,重塑黄土与原状软黏土竖向塑性累积应变对比图。
由图 11可知,原状软黏土在未发生破坏时,其竖向塑性累积应变约为重塑黄土的10倍,在发生破坏时,其竖向塑性累积应变约为重塑黄土的100倍,这是因为相较于原状软黏土,重塑黄土由于击实作用,其压缩模量远远大于原状软黏土,因此原状软黏土在外力扰动作用下,更易发生较大变形。此外,值得注意的是当CVSR=0.2,η=0.3,循环次数约为8000时,原状软黏土的竖向塑性累积应变发生突变,土体发生了破坏,而重塑黄土在本次试验中未发生破坏。这进一步表明重塑黄土相较于原状软黏土作为路基填筑材料的优越性。
3. 竖向塑性累积变形计算模型
3.1 竖向塑性累积变形计算模型的建立
基于上述所获得的空心扭剪试验结果,本文在Monismith模型[23]的基础上提出了适用于重塑饱和黄土路基竖向应变累积的显式模型,Monismith模型如下式:
εp=αNβ, (5) 式中,N为循环次数,α和β为拟合参数。
本文在此基础上,引入循环扭剪应力比η和循环竖向应力比CVSR,从而建立较为完善的黄土路基沉降预测模型。通过对试验数据的进一步处理,发现试样在经过200次循环后,竖向塑性累积应变lg(εPz)与循环次数lg(N)基本呈线性变化关系,如图 12所示。所以根据式(4)提出如下假设:
lg(εpz)=k[lg(N)−lg(200)]+lg(εpz,200), (6) 式中,k为拟合曲线斜率,εPz为第200次循环后试样的竖向塑性累积应变。
对比图 12中的拟合曲线可发现,线性拟合后,拟合线斜率基本保持不变,由此可说明k与循环应力比和循环竖向应力比均无相关性。因此,k值取12组数据的加权平均值,即k=0.112。而截距lg(εpz,200)随CVSR和η具有显著的相关性。为此,本文提出以CVSR和η为自变量,lg(εpz,200)为因变量,采用Origin软件进行二元非线性拟合,拟合函数采用Poly 2D函数,具体数学模型表达式为
εpz,200=m+a×CVSR+b×η+c×(CVSR)2+d×η2+n×CVSR×η。 (7) 基于循环次数为200时的竖向塑性累积应变的试验数据以及Poly 2D函数开展二元非线性拟合。求解得出其中的参数m,a,b,c,d,n分别为0.049,-0.650,-0.051,3.050,0.367和0.036。将式(7)带入式(6)中,进而得到完整的饱和重塑黄土路基沉降的显式预测模型,即
εpz=(N200)0.112×(0.049−0.65CVSR−0.051η+3.05×CVSR2+0.367×η2+0.036η×CVSR)。 (8) 3.2 竖向塑性累积变形计算模型的验证
为验证上述预测模型的准确性,本文设置了一组与试验方案相同的平行试验,并将预测值与其试验结果进行了对比验证,结果如图 13所示。
从图 13可以看出,通过式(8)得到的竖向塑性累积应变与通过扭剪试验得到的累积应变基本吻合。计算模型对不同循环扭剪应力比η和循环竖向应力比CVSR均有一定的预测效果。因此,该计算模型能较好地适用于重塑饱和黄土的循环三轴试验累积应变的预测,同时通过引入CVSR和η两个系数也能较好反映主应力轴旋转对竖向塑性累积应变产生的影响。
4. 结论
通过开展不同循环应力比下重塑黄土的空心圆柱扭剪试验,主要针对循环扭剪应力比和循环竖向应力比对试样竖向应变、径向应变以及八面体剪应变的影响展开分析,并与饱和软黏土的变形特性进行了比较,且基于试验结果建立了黄土路基沉降变形的显式预测模型,最终通过已有结果与试验结果对比验证了模型的有效性。主要结论如下:
(1)土样的竖向塑性累积应变和八面体剪应变随循环次数呈对数型增长趋势,在循环次数达到1000次时,应变增长速率趋于平缓。
(2)试样竖向塑性累积变形增长速率随循环次数变化的变化规律与主应力轴是否发生旋转无关,但应力主轴的旋转会加速累积沉降变形的产生,循环交通荷载对路基的沉降变形有着显著的影响。
(3)对竖向累积应变和八面体累积应变而言,累积应变终值与循环扭剪应力比η和循环竖向应力比CVSR均呈正相关。对径向累积应变而言,累积应变终值主要受CVSR影响,与η相关性并不显著。
(4)经试验数据验证,建立的同时考虑CVSR和η影响的竖向塑性累积应变的计算模型适用性良好。
-
表 1 离散元模拟微观力学参数
Table 1 Micromechanical parameters of numerical samples
参数 颗粒粒径/mm 颗粒密度/(kg·m-3) 颗粒-颗粒摩擦系数 颗粒接触法向刚度/(N·m-1) 颗粒接触刚度比 量值 0.5~0.9 2600 0.75 1×107 1.5 -
[1] CASTRO G. Liquefaction of Sands[D]. Boston: Harvard University, 1969.
[2] LADE P V, PRADEL D. Instability and plastic flow of soils: I experimental observations[J]. Journal of Engineering Mechanics, 1990, 116(11): 2532-2550. doi: 10.1061/(ASCE)0733-9399(1990)116:11(2532)
[3] LANCELOT L, SHAHROUR I, MAHMOUD M A. Instability and static liquefaction on proportional strain paths for sand at low stresses[J]. Journal of Engineering Mechanics, 2004, 130(11): 1365-1372. doi: 10.1061/(ASCE)0733-9399(2004)130:11(1365)
[4] LADE P V. Static instability and liquefaction of loose fine sandy slopes[J]. Journal of Geotechnical Engineering, 1992, 118(1): 51-71. doi: 10.1061/(ASCE)0733-9410(1992)118:1(51)
[5] KRAFT L M, GAVIN T M, BRUTON J C. Submarine flow slide in Puget Sound[J]. Journal of Geotechnical Engineering, 1992, 118(10): 1577-1591. doi: 10.1061/(ASCE)0733-9410(1992)118:10(1577)
[6] 符新军, 赵仲辉. 饱和粉砂不稳定性的试验研究[J]. 岩土力学, 2008, 29(2): 381-385. doi: 10.3969/j.issn.1000-7598.2008.02.017 FU Xin-jun, ZHAO Zhong-hui. Laboratory study of the instability of saturated silty sand[J]. Rock and Soil Mechanics, 2008, 29(2): 381-385. (in Chinese) doi: 10.3969/j.issn.1000-7598.2008.02.017
[7] 章根德, 韦昌富, 江礼茂. 饱和砂土的非稳定性[J]. 岩土工程学报, 1994, 16(6): 39-46. doi: 10.3321/j.issn:1000-4548.1994.06.005 ZHANG Gen-de, WEI Chang-fu, JIANG Li-mao. The instability of saturated sand[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(6): 39-46. (in Chinese) doi: 10.3321/j.issn:1000-4548.1994.06.005
[8] MRÓZ Z, BOUKPETI N, DRESCHER A. Constitutive model for static liquefaction[J]. International Journal of Geomechanics, 2003, 3(2): 133-144. doi: 10.1061/(ASCE)1532-3641(2003)3:2(133)
[9] DESAI C S, PRADHAN S K, COHEN D. Cyclic Testing and constitutive modeling of saturated sand-concrete interfaces using the disturbed state concept[J]. International Journal of Geomechanics, 2005, 5(4): 286-294. doi: 10.1061/(ASCE)1532-3641(2005)5:4(286)
[10] RAHMAN M M, BAKI M A L, LO S R. Prediction of undrained monotonic and cyclic liquefaction behavior of sand with fines based on the equivalent granular state parameter[J]. International Journal of Geomechanics, 2014, 14(2): 254-266. doi: 10.1061/(ASCE)GM.1943-5622.0000316
[11] 马刚, 常晓林, 刘嘉英, 等. 颗粒物质在等比例应变加载下的分散性失稳模式[J]. 岩土力学, 2015, 36(增刊1): 181-186. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S1030.htm MA Gang, CHANG Xiao-lin, LIU Jia-ying, et al. Diffusion failure mode of granular materials under proportional strain path loading[J]. Rock and Soil Mechanics, 2015, 36(S1): 181-186. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S1030.htm
[12] CHU J, LO S R, LEE I K. Instability of granular soils under strain path testing[J]. Journal of Geotechnical Engineering, 1993, 119(5): 874-892. doi: 10.1061/(ASCE)0733-9410(1993)119:5(874)
[13] LANCELOT L, SHAHROUR I, MAHMOUD M A. Instability and static liquefaction on proportional strain paths for sand at low stresses[J]. Journal of Engineering Mechanics, 2004, 130(11): 1365-1372. doi: 10.1061/(ASCE)0733-9399(2004)130:11(1365)
[14] JRAD M, SUKUMARAN B, DAOUADJI A. Experimental analyses of the behaviour of saturated granular materials during axisymmetric proportional strain paths[J]. European Journal of Environmental and Civil Engineering, 2012, 16(1): 111-120. doi: 10.1080/19648189.2012.666900
[15] ECKERSLEY J D. Instrumented laboratory flow slides[J]. Géotechnique, 1990, 40(3): 489-502. doi: 10.1680/geot.1990.40.3.489
[16] OLSON S M, STARK T D, WALTON W H. 1907 Static liquefaction flow failure of the north dike of Wachusett dam[J]. Journal of Geotechnical and Geo-environmental Engineering, 2000, 126(12): 1184-1193. doi: 10.1061/(ASCE)1090-0241(2000)126:12(1184)
[17] HILL R. A general theory of uniqueness and stability in elastic-plastic solids[J]. Journal of the Mechanics and Physics of Solids, 1958, 6(3): 236-249. doi: 10.1016/0022-5096(58)90029-2
[18] SASITHARAN S, ROBERTSON P K, SEGO D C, et al. Collapse behavior of sand[J]. Canadian Geotechnical Journal, 1993, 30(4): 569-577. doi: 10.1139/t93-049
[19] SKOPEK P, MORGENSTERN N R, ROBERTSON P, et al. Collapse of dry sand[J]. Canadian Geotechnical Journal, 1994, 31(6): 1008-1014. doi: 10.1139/t94-115
[20] ANDERSON S A, RIEMER M F. Collapse of saturated soil due to reduction in confinement[J]. Journal of Geotechnical Engineering, 1995, 121(2): 216-220. doi: 10.1061/(ASCE)0733-9410(1995)121:2(216)
[21] CHU J, S L , LEONG W K. Unstable behavior of sand and its implication for slope instability[J]. Canadian Geotechnical Journal, 2003, 40(5): 873-885. doi: 10.1139/t03-039
[22] LADE P V, PRADEL D. Instability and plastic flow of soils I: experimental observations[J]. Journal of Engineering Mechanics, 1990, 116(11): 2532-2550. doi: 10.1061/(ASCE)0733-9399(1990)116:11(2532)
[23] LEONG W K, CHU J, TEH C I. Liquefaction and instability of a granular fill material[J]. Geotechnical Testing Journal, 2000, 23(2): 178-192. doi: 10.1520/GTJ11042J
[24] MONKUL M M, YAMAMURO J A, LADE P V. Failure, instability, and the second work increment in loose silty sand[J]. Canadian Geotechnical Journal, 2011, 48(6): 943-955. doi: 10.1139/t11-013
[25] CHU J, LEONG W K, LOKE W L, et al. Instability of loose sand under drained conditions[J]. Journal of Geotechnical & Geo-environmental Engineering, 2012, 138(2): 207-216.
[26] DONG Q, XU C, CAI Y, et al. Drained instability in loose granular material[J]. International Journal of Geomechanics, 2015, 16(2): 04015043.
[27] 董全杨, 蔡袁强, 王军, 等. 松散砂土不稳定性试验研究[J]. 岩石力学与工程学报, 2014(3): 623-630. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201403024.htm DONG Quan-yang, CAI Yuan-qiang, WANG Jun, et al. Experimental study of instability of loose sand[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014(3): 623-630. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201403024.htm
[28] DAOUADJI A, ALGALI H, DARVE F, et al. Instability in granular materials: experimental evidence of diffuse mode of failure for loose sands[J]. Journal of Engineering Mechanics, 2010, 136(5): 575-588. doi: 10.1061/(ASCE)EM.1943-7889.0000101
[29] DAOUADJI A, HICHER P Y, JRAD M, et al. Experimental and numerical investigation of diffuse instability in granular materials using a microstructural model under various loading paths[J]. Géotechnique, 2013, 63(5): 368-381. doi: 10.1680/geot.10.P.121
[30] DARVE F, LAOUAFA F, SERVANT G, et al. Continuous and discrete analyses of failure in geomaterials[J]. Computer Methods in Applied Mechanics & Engineering, 2004, 193(27): 3057-3085.
[31] DARVE F, SIBILLE L, DAOUADJI A, et al. Bifurcations in granular media: macro and micro-mechanics approaches[J]. Comptes Rendus Mécanique, 2007, 335(9/10): 496-515.
[32] ORENSE R, FAROOQ K, TOWHATA I. Deformation behavior of sandy slopes during rainwater infiltration[J]. Soils and Foundations, 2004, 44(2): 15-30. doi: 10.3208/sandf.44.2_15
[33] WANATOWSKI D, CHU J, LOKE W L. Drained instability of sand in plane strain[J]. Canadian Geotechnical Journal, 2010, 47(4): 400-412. doi: 10.1139/T09-111
[34] CHU J, WANATOWSKI D, LEONG W K, et al. Instability of dilative sand[J]. Geotechnical Research, 2015, 2(1): 35-48.
[35] FAN M, LIU Y, HAN J, et al. Numerical investigation of diffuse instability in sandy soil using discrete element method under proportional strain path loading[J]. Latin American Journal of Solids and Structures, 2018, 15(11): e134.
[36] FEIA S, SULEM J, CANOU J, et al. Changes in permeability of sand during triaxial loading: effect of fine particles production[J]. Acta Geotech, 2016, 11(1): 1-19.
-
期刊类型引用(5)
1. 窦杰,向子林,许强,郑鹏麟,王协康,苏爱军,刘军旗,罗万祺. 机器学习在滑坡智能防灾减灾中的应用与发展趋势. 地球科学. 2023(05): 1657-1674 .  百度学术
百度学术
2. 姚未来,刘元雪,陈进,程香. 新工科背景下岩土工程学科研究生培养科研支架式教学模式构建. 高等建筑教育. 2022(02): 66-76 .  百度学术
百度学术
3. 董亮,阚新生,邓国如,徐杰,袁慧. 短期电力负荷预测的时间序列数据深度挖掘模型设计. 能源与环保. 2021(06): 207-212 .  百度学术
百度学术
4. 刘元雪,姚未来,陈进,郑颖人. 建构“创新”基因, 改革岩土塑性力学研究生教材. 高等工程教育研究. 2021(05): 100-105 .  百度学术
百度学术
5. 刘洋,于鹏强,张铎,王肖肖. 一个基于微观力学分析的散粒体应力–剪胀关系. 岩土工程学报. 2021(10): 1816-1824 .  本站查看
本站查看
其他类型引用(2)




 下载:
下载: