考虑颗粒排列的土体几何迂曲度模型

颜瀚; 滕继东; 张升; 盛岱超

doi:10.11779/CJGE202001023

考虑颗粒排列的土体几何迂曲度模型 English Version

颜瀚^1,,
滕继东^{1, 2},
张升^{1, 2, ,},
盛岱超^{1, 2}

1.
中南大学土木工程学院,湖南　长沙　410075
2.
中南大学高速铁路建造技术国家工程实验室,湖南　长沙　410075

基金项目:

国家自然科学基金优秀青年基金项目 51722812

湖南省自然科学基金项目 2017JJ1033

国家自然科学基金项目 51878665

国家自然科学基金项目 U1834206

铁路总公司重大研究计划项目 K2018G019

详细信息

作者简介:
颜瀚（1994— ）,男,硕士研究生,主要从事冻土渗流方面的研究工作。E-mail：yanhanxy@csu.edu.cn

通讯作者:
张升, E-mail：zhang-sheng@csu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 327
- HTML全文浏览量: 24
- PDF下载量: 264
出版历程
- 收稿日期: 2019-02-21
- 网络出版日期: 2022-12-07
- 刊出日期: 2019-12-31

Model for tortuosity of soil considering geometric arrangement of particles

YAN Han^1,,
TENG Ji-dong^{1, 2},
ZHANG Sheng^{1, 2, ,},
SHENG Dai-chao^{1, 2}

1.
Department of Geotechnical Engineering, Central South University, Changsha 410075, China
2.
National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China

摘要

摘要: 迂曲度反映了流体在土颗粒中的流动路径,是研究土体透水透气性质的重要参数。目前研究通常认为迂曲度仅与孔隙率有关,但不同文献的迂曲度表达式存在一定差异,造成差异的原因可能是存在其他影响迂曲度的因素。建立了流体在层流状态下通过正方形颗粒的物理模型,通过确定颗粒间位置关系和流径的几何关系,提出了迂曲度计算模型。同时,对比结果表明本文模型的计算结果与数值模拟结果、文献中试验结果存在很好的一致性,证明了模型的有效性。最后,分析了颗粒排列分布对迂曲度的影响,确定了迂曲度的取值区域。提出的模型证实：颗粒的迂曲度不是孔隙率的单一函数,排列分布也对迂曲度有影响。
- 迂曲度 /
- 孔隙率 /
- 颗粒排列 /
- 渗透
Abstract: Tortuosity is an important parameter in studying the permeability of soil, which reflects the flow path of fluid in soil particles. In literatures, the tortuosity is considered to be solely related to the porosity of soil. However, the expressions for the tortuosity vary greatly in the previous studies. It may be caused by some other unconsidered factors. The physical model for fluid passing through square particles in laminar flow state is established in this study. The results show that the proposed model agrees well with the numerical simulation results and the experimental results in the literatures. Finally, the influences of particle arrangement and distribution on the tortuosity are analyzed, and the value region of the tortuosity is determined. It is concluded that the tortuosity of particles relates to the porosity of soil and the distribution of particles.
- tortuosity /
- porosity /
- particle arrangement /
- permeability

HTML全文

0. 引言

“锅盖效应”是由李强等^[1]提出的用以描述土中的水汽，因毛细作用、温度作用、蒸发等作用向土体表面迁移的过程中，受到地表不透气的覆盖层的阻碍，而在覆盖层下积聚的现象。

“锅盖效应”广泛存在于建筑、公路、机场等工程中，沈阳桃仙机场在其地下水位极低（埋深28~35 m）的情况下，在机场跑道道面下积聚了大量水而对跑道造成损害^[2]；敦煌机场跑道道面下的水汽不能有效蒸发，在道面以下不断下降的冰冻线附近结成冰，造成道面鼓胀变形破坏^[3]；斯堪的纳维亚、加拿大北部和美国北部的某些路面和颗粒基层之间的界面处凝结的水分过多^[4]，造成柔性路面的过早失效。建筑物基础、公路路面和机场跑道形成的“锅盖”，可能会导致土中含水量分布发生改变，这将影响土体的变形和承载力，也可能给道面带来冻胀、唧泥、掉角、断板以及不均匀沉降等一系列工程灾害。因此，对于“锅盖效应”的发生机理探讨、试验再现、防范措施也开始进入了大规模的探索和研究阶段^[5-10]。

目前，非饱和土的冻胀研究极少开展，传统的非饱和土渗流理论常常忽略低温条件下水汽的迁移特征和规律，而传统冻土理论也多基于饱和土渗流理论，关注液态水的冻结和集聚作用，较少涉及气态水的迁移。然而，Milly^[11]通过非饱和土试验、Miyazaki^[12]通过一维土体湿热空气扩散试验，Anthony等^[13]通过裸地土壤的现场试验，均发现气态水在土中的迁移现象非常明显。Zhang^[14]等在对“锅盖效应”的研究中，采用荧光示踪剂来追踪土壤未冻结的液态水的位置，更进一步证实了“锅盖效应”中气态水迁移的重要影响。

因此本文在前人研究的基础上，考虑了土体的土颗粒骨架结构、孔隙率、饱和度、蒸汽压、以及温度对“锅盖效应”气态水迁移的影响，基于PDV经典水汽迁移模型，推导出在“锅盖效应”的框架内的一维气态水迁移方程，并分析了温度与饱和度对“锅盖效应”气态水迁移通量的影响，为“锅盖效应”的研究提供帮助。

1. 一维“锅盖效应”气态水迁移方程

1.1 “锅盖效应”的机理

“锅盖效应”是一种土中的水汽迁移现象，土层道基以下的地下水是“锅盖效应”的主要水来源，地下水在毛细作用下向上迁移，但当地下水位较深的时候，如沈阳桃仙机场，地下水埋深约28~35 m，毛细作用很难上升这么大的高度，此时在道面零下低温的条件下，温度梯度的作用使气态水的迁移成为了土层道基中水汽迁移的主要组成部分，气态水在土层道基中向上迁移至道面下的碎石层中，被不透气的道面所阻挡，而碎石层的温度较低，因此气态水在碎石层中凝结成液态水，并积累在碎石层中，如图 1所示。

图 1 “锅盖效应”的发生机理

Figure 1. Mechanism of "pot cover effect"

下载: 全尺寸图片幻灯片

1.2 一维“锅盖效应”气态水迁移方程的建立

土体内的水汽迁移十分复杂，Sherwood^[15]认为土体水汽迁移的驱动势是土体的湿含量梯度；Cealglske等^[16]认为驱动势为土体内部的毛细管势能；Henry^[17]认为是土体内的蒸汽扩散。但单一的驱动势是无法很好地描述土体内水汽迁移的真实现象。Philip等^[18]提出的非饱和土壤中水汽迁移的双场模型，作为以温度梯度和湿分梯度为驱动势的双场模型，该模型着重考虑到了土体气相的水分传输，这印证了目前“锅盖效应”现象中土体中气态水迁移的重要影响，这也是本文采用该模型作为“锅盖效应”气态水迁移方程理论基础的原因。该模型提出了水蒸气通过非饱和土壤的流动机制：

${V_{\text{v}}} = - \frac{{{D_{{\text{atms}}}}\nu \tau {\theta _{\text{a}}}}}{{{\rho _{\text{w}}}}}\nabla {\rho _{\text{v}}} \text{，}$

(1)

式中 ${V_{\text{v}}}$ 为水蒸气的速度； ${V_{\text{v}}}$ 为扩散系数；ν为质量流因子；τ为土壤迂曲度； ${\theta _{\text{a}}}$ 为单位体积空气的含量； ${\rho _{\text{v}}}$ 为水蒸气的密度； ${\rho _{\text{w}}}$ 为液态水的密度； $\nabla {\rho _{\text{v}}}$ 为水蒸气的密度梯度。

对于单位体积空气的含量，有

${\theta _{\text{a}}} = \varphi - {\theta _{\text{w}}} \text{，}$

(2)

式中，φ为孔隙率， ${\theta _{\text{w}}}$ 为单位体积的液态水含量。

土壤的孔隙气体则可以作为孔隙干燥空气与孔隙水蒸气组成的二元混合物。在土体内气态水的迁移过程中，存在着与孔隙液态水之间的冷凝与蒸发，维持着动态平衡，因此可以认为孔隙液态水与孔隙气态水之间的冷凝与蒸发速率相同，任意一点上单位体积的液态水与气态水处于平衡状态^[19]，此时液态水与气态水之间界面的曲率则决定蒸汽分压，而土体的饱和度则决定的液态水与气态水之间界面的曲率，因此蒸汽压力与多孔介质的液体饱和度存在函数关系。

从热力学可知，流体的绝对自由能G是分子离开该相倾向的一种量度。对于“锅盖效应”中土体孔隙中与蒸汽处于平衡状态的液态水，其液态水的自由能 ${G_{\text{w}}}$ 应等于蒸汽的自由能 ${G_{\text{v}}}$ 。如果出现从一个平衡状态的过渡，则一定有 ${\text{d}}{G_{\text{w}}} = {\text{d}}{G_{\text{v}}}$ 。

假定液态水的压力改变一个微量 ${\text{d}}{u_{\text{w}}}$ ，在蒸汽压力中必将发生相应的改变 ${\text{d}}{u_{\text{v}}}$ ，于是有

${V_{\text{w}}}{\text{d}}{u_{\text{w}}} = {V_{\text{v}}}{\text{d}}{u_{\text{v}}} \text{，}$

(3)

式中 ${V_{\text{w}}}$ 和 ${V_{\text{v}}}$ 为液态水和蒸汽的比摩尔容积； ${u_{\text{v}}}$ 为蒸汽分压； ${u_{\text{w}}}$ 为孔隙水压力。

将蒸汽视作理想气体，则有

${V_{\text{v}}} = \frac{{RT}}{{{u_{\text{v}}}}} \text{，}$

(4)

式中，R为气体常数，R=461.52 J/kg·K，T为温度。

液态水的体积 ${V_{\text{w}}}$ 可以写作

${V_{\text{w}}} = \frac{M}{\rho } \text{，}$

(5)

式中，M为摩尔质量， $\rho$ 为液体密度。

将式（4），（5）代入到式（3）中，则可以得到

$\frac{{{\text{d}}{u_{\text{v}}}}}{{{u_{\text{v}}}}} = \frac{M}{{\rho RT}}{\text{d}}{\rho _{\text{w}}} 。$

(6)

两边同时积分有

${u_{\text{v}}} = {u_{{\text{v0}}}}h = {u_{{\text{v0}}}}\exp \left[ { - {u_{\text{c}}}\left( {\frac{ M}{{\rho PT}}} \right)} \right] \text{，}$

(7)

式中， ${u_{{\text{v0}}}}$ 为饱和蒸汽压。

“锅盖效应”中的土体为非饱和土体，因此存在基质吸力会对水蒸气的迁移造成影响。Fredlund等^[20]将基质吸力定义为孔隙空气压力与孔隙液体压力之差，表示为

${u_{\text{c}}} = {u_{\text{a}}} - {u_{\text{w}}} 。$

(8)

式中， ${u_{\text{c}}}$ 为基质吸力。

将式（8）代入到式（7），并引入相对湿度h，可得出

${u_{\text{v}}} = {u_{{\text{v0}}}}h = {u_{{\text{v0}}}}\exp \left[ { - {u_{\text{c}}}\left( {\frac{M}{{\rho PT}}} \right)} \right] \text{，}$

(9)

式中，h为相对湿度。

根据Ewen等^[21]的理论，浓度梯度 $\nabla {\rho _{\text{v}}}$ 取决于温度与含水率，可以表示为

$\nabla {\rho }_{\text{v}}=\left(h\frac{\partial {u}_{\text{v0}}}{\partial T}+{u}_{\text{v0}}\frac{\partial h}{\partial T}\right)\nabla T+\left({\rho }_{0}\frac{\partial h}{\partial {S}_{\text{r}}}\right)\nabla {u}_{\text{a}}-\left({\rho }_{0}\frac{\partial h}{\partial {S}_{\text{r}}}\right)\nabla {u}_{\text{w}}。$

(10)

通过气体的绝对浓度公式，则可以得到单位体积内的气态水水分含量：

$C = \frac{{{u_{\text{v}}}}}{{RT}} = \frac{{{u_{{\text{v0}}}}h}}{{RT}} 。$

(11)

此时对于“锅盖效应”单位时间内某一截面通过的气态水的量，可以用通量来表示，即单位时间内该截面的气态水水分含量与气态水迁移速率的乘积，因此通量公式写作：

$\begin{aligned} & J=\frac{u_{\mathrm{v} 0} h}{R T} \cdot \frac{-D_{\mathrm{atms}} v \tau\left(\varphi-\theta_{\mathrm{w}}\right)}{\rho_{\mathrm{w}}} \cdot \\ & {\left[\left(h \frac{\partial u_{\mathrm{v} 0}}{\partial T}+u_{\mathrm{v} 0} \frac{\partial h}{\partial T}\right) \nabla T+\left(\rho_0 \frac{\partial h}{\partial S_{\mathrm{r}}}\right) \nabla u_a-\left(\rho_0 \frac{\partial h}{\partial S_{\mathrm{r}}}\right) \nabla u_{\mathrm{w}}\right] 。} \end{aligned}$

(12)

将式（8）代入可以得到

$\begin{aligned} J=& \frac{u_{\mathrm{v} 0} h}{R T} \cdot \frac{-D_{\mathrm{atms}} v \tau\left(\varphi-\theta_{\mathrm{w}}\right)}{\rho_{\mathrm{w}}} \cdot \\ & \ \ \ \ \ {\left[\left(h \frac{\partial u_{\mathrm{v} 0}}{\partial T}+u_{\mathrm{v} 0} \frac{\partial h}{\partial T}\right) \nabla T+\left(\rho_0 \frac{\partial h}{\partial S_{\mathrm{r}}}\right) \nabla u_{\mathrm{c}}\right] 。 } \end{aligned}$

(13)

若引入土水特征曲线常用的VG模型，则可以表示土体饱和度与基质吸力的关系，即

${S_{\text{r}}} = f({u_{\text{c}}}) = \frac{1}{{{{\left[ {1 + {{(a{u_{\text{c}}})}^n}} \right]}^{(1 - \frac{1}{n})}}}} \text{，}$

(14)

式中，S_r为饱和度，a与n为模型参数。

将式（14）代入到式（9）中，则可以得到

$h = \exp \left( {\frac{{{{({S_{\text{r}}}^{\frac{n}{{1 - n}}} - 1)}^{\frac{1}{n}}}}}{{ - a{\rho _{\text{w}}}{R_{\text{v}}}T}}} \right) 。$

(15)

式（15）可以表示出土体孔隙气相相对湿度与土体饱和度的关系，并且利用 $\nabla {u_{\text{c}}} = \frac{{\partial {u_{\text{c}}}}}{{\partial {S_{\text{r}}}}} \cdot \nabla {S_{\text{r}}}$ ，那么式（13）可表示为温度梯度与饱和度梯度双驱动势的迁移通量公式：

$\begin{aligned} J= & \frac{u_{\mathrm{v} 0} h}{R T} \cdot \frac{-D_{\mathrm{atms}} v \tau\left(\varphi-\theta_{\mathrm{w}}\right)}{\rho_{\mathrm{w}}} . \\ & \ \ {\left[\left(h \frac{\partial u_{\mathrm{v} 0}}{\partial T}+u_{\mathrm{v} 0} \frac{\partial h}{\partial T}\right) \nabla T+u_{\mathrm{v} 0} \frac{\partial h}{\partial S_{\mathrm{r}}} \cdot \frac{\partial u_{\mathrm{c}}}{\partial S_{\mathrm{r}}} \nabla S_{\mathrm{r}}\right] 。 } \end{aligned}$

(16)

式（16）表示，“锅盖效应”气态水迁移过程中，在温度梯度与饱和度梯度双驱动势作用下的单位截面积上气态水迁移的通量。式（16）表明温度、相对湿度、蒸汽压、饱和度、土体结构对“锅盖效应”气态水迁移具有重要影响，物理明确。

参考陈含进行的“锅盖效应”室内试验作用^[22]，试验原理如图 2所示。

图 2 “锅盖效应”的试验原理

Figure 2. Test principle of "pot cover effect"

下载: 全尺寸图片幻灯片

设计如下试验条件：

土样采用纯细砾。试验筒顶部和底部控制不同的恒定温度，形成温度梯度，气态水在温度梯度的作用下向上迁移，因为砾石层孔隙较大以及砾石的持水能力较差等特点，气态水在砾石层中凝结为液态水后会因为重力作用下渗至饱和砾石层。对于重力作用下渗的液态水，其重力下渗的启动条件为“临界饱和状态”，即凝结的液态水的重力与土体的持水能力达到平衡的状态，陈含^[22]经过试验总结出选用的砾石持水度和温度具有如下关系：

${\theta _{\text{r}}} = - 0.001 \cdot T + 0.32 。$

(17)

Partington^[23]对于封闭系统中蒸发源与冷凝之间的稳态扩散，提出的质量流动因子ν的表达式如下：

$\nu = \frac{{{u_{\text{a}}}}}{{{u_{\text{a}}} - {u_{\text{v}}}}} 。$

(18)

对于饱和蒸汽压力，本文采用修正的Tetens饱和蒸汽压公式：

${u_{{\text{v0}}}} = 6.112\exp \left( {\frac{{17.67(T - 273.15)}}{{T - 29.65}}} \right) 。$

(19)

因为“锅盖效应”系统的顶部和底部分别设置有恒定温度，对于系统内的温度梯度，则可以视作沿系统高度的稳态温度场分布，因此温度梯度可视作常数：

$\frac{{\partial T}}{{\partial x}} = \frac{{{T_{\text{t}}} - {T_{\text{b}}}}}{{{x_{\text{t}}} - {x_{\text{b}}}}} \text{，}$

(20)

式中 ${T_{\text{t}}}$ 与 ${T_{\text{b}}}$ 为系统顶部与底部的温度； ${x_{\text{t}}}$ 与 ${x_{\text{b}}}$ 为系统顶部与底部在x方向上的长度。

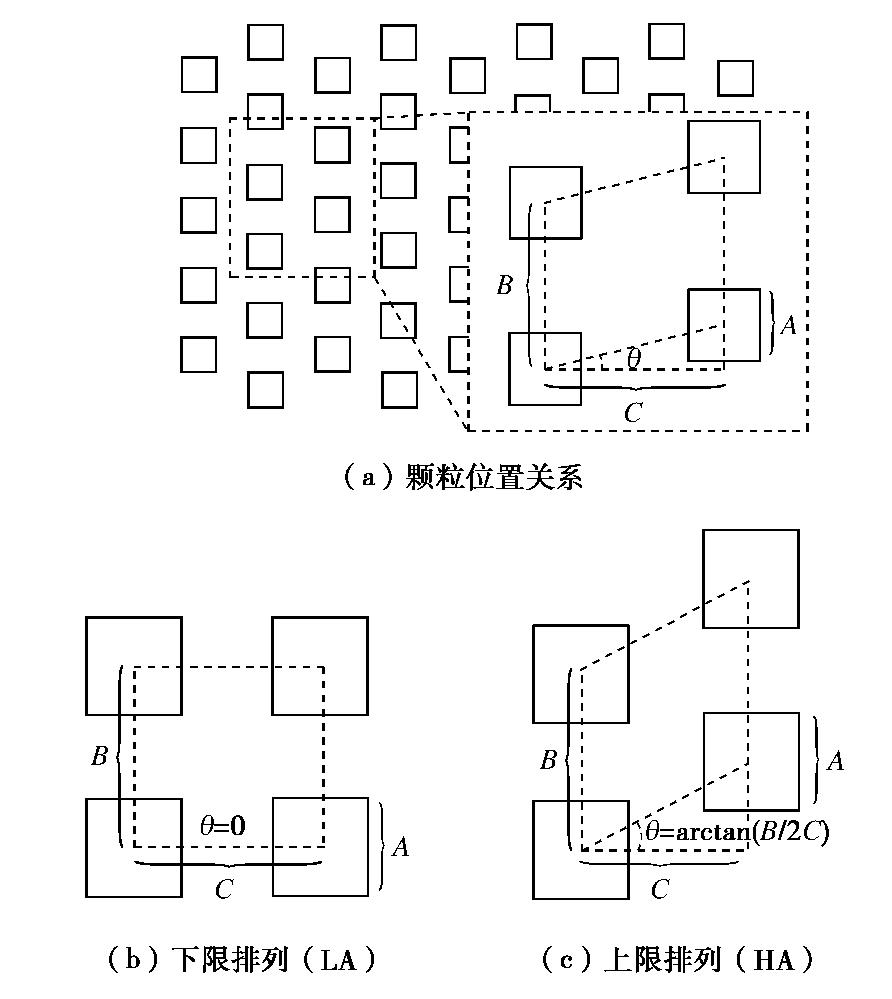
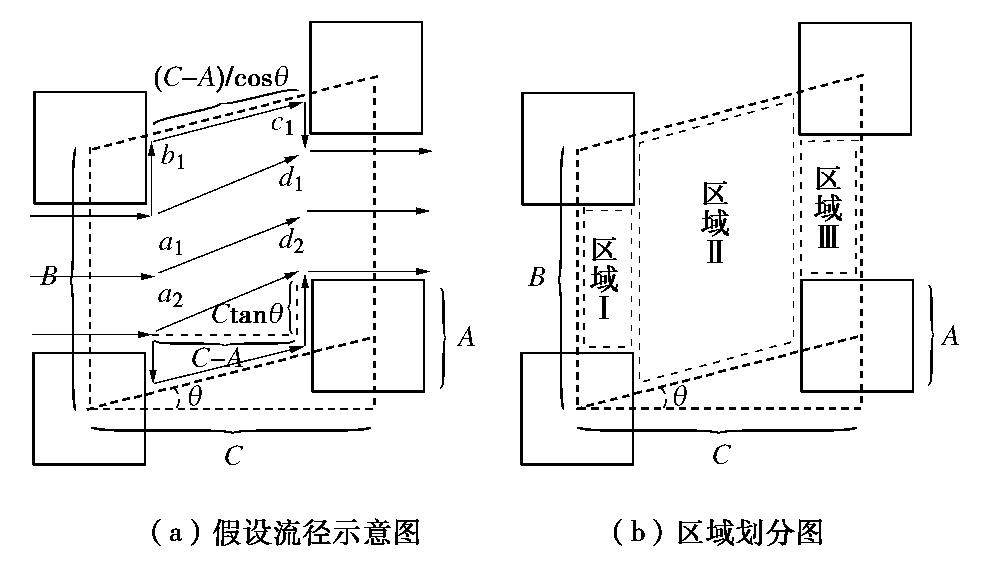
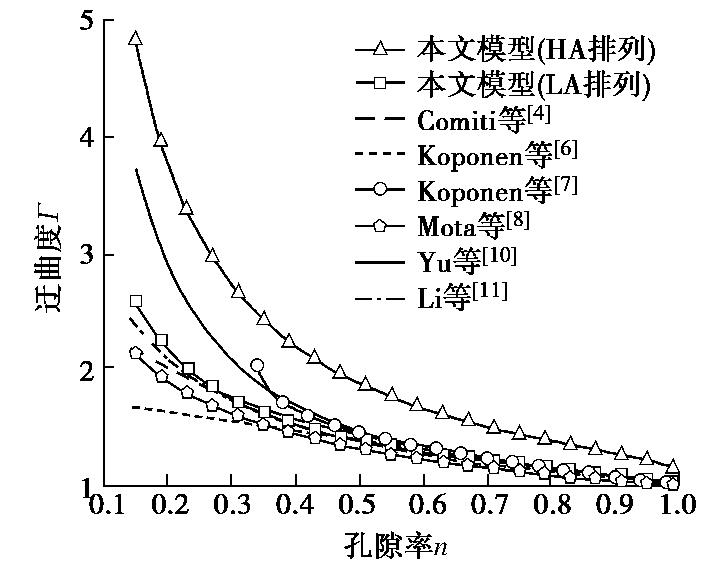
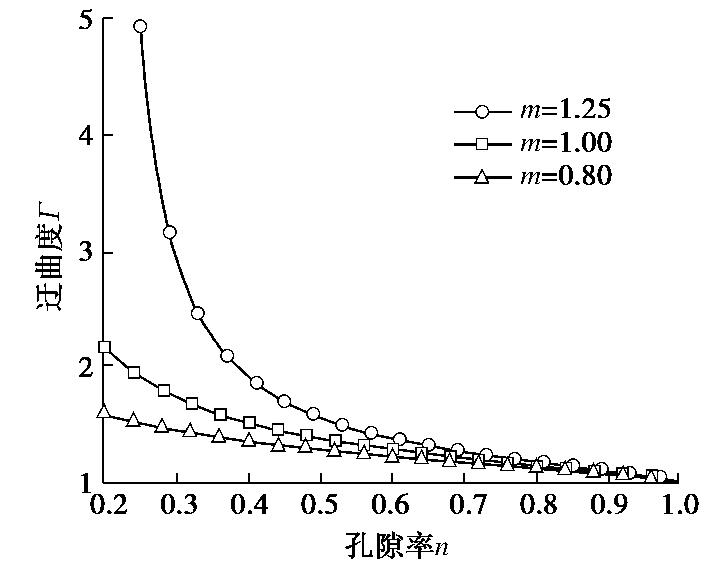
对于土壤迂曲度τ，本文采用Koponen^[24]提出的用孔隙率的函数来表示的土壤迂曲度表达式，即

$\tau = {\left[ {0.8(1 - n) + 1} \right]^{ - 1}} 。$

(21)

对于扩散系数D_atms，Krischer^[25]给出了蒸汽相相对于空气的分子扩散系数经验公式：

${D_{{\text{atms}}}} = 5.893 \times {10^{ - 6}}\frac{{{T^{2.3}}}}{{{u_{\text{a}}}}} 。$

(22)

对于该试验中的土样，砾石层的含水率为临界饱和状态，即θ_r；砾石的G_s=2.61，干密度ρ_d=1.40 g/cm³，孔隙率φ=46.4%；仪器顶部恒温T_t=0.3℃，底部恒温T_b=20℃，仪器高度45 cm，因此温度梯度 $\nabla T$ 取0.4378℃/cm；土水特征曲线参考文献[26]中细砾VG模型的拟合参数a=0.077，n=1.20。

将上述试验条件以及式（17）~（22）代入到式（16）中分别分析温度与饱和度对“锅盖效应”气态水迁移通量的影响。

（1）温度对“锅盖效应”气态水迁移的影响

按照上述试验条件，控制砾石的饱和度恒定为10%，绘制温度对“锅盖效应”气态水迁移的影响，如图 3所示。

图 3 迁移通量J与温度T的关系曲线

Figure 3. Relationship between diffusion flux J and temperature T

下载: 全尺寸图片幻灯片

从图 3可以看出温度对“锅盖效应”气态水迁移通量具有正相关影响，随着温度的增加，迁移通量也会增大。

（2）饱和度对“锅盖效应”气态水迁移的影响

控制砾石的温度恒定为10℃，绘制土体饱和度对“锅盖效应”气态水迁移的影响，如图 4所示。

图 4 迁移通量J与饱和度S_r的关系曲线

Figure 4. Relationship between diffusion flux J and soil saturation S_r

下载: 全尺寸图片幻灯片

从图 4可以看出，随着饱和度的增加，“锅盖效应”气态水的迁移通量呈现先增大后减小的规律，这与文献[5]试验所发现的水汽迁移系数与土体含水率的关系曲线较为一致。在饱和度很低的时候，气态水与液态水的含量都很低，因此迁移通量也很低，并且由于土颗粒的持水能力，气态水很容易就附着在土颗粒的表面形成吸附水，因此迁移通量接近0；随着饱和度的增加，土颗粒无法吸附更多的水，气态水更容易通过土体孔隙，因此迁移通量也在增加；当饱和度进一步增加，孔隙中的液态水含量较高，土体孔隙被液态水所占据，削弱了气态水浓度梯度作为驱动势的影响，因此造成了迁移通量的减小。

2. 结论

基于已有的水汽迁移模型，推导了在“锅盖效应”框架内一维气态水迁移的方程，并分析了温度与饱和度对“锅盖效应”气态水迁移的影响，得到如下结论：

（1）以PDV模型为基础，考虑到温度、相对湿度、蒸汽压、含水率、土体结构、水蒸气密度梯度对“锅盖效应”气态水迁移的影响，推导出一维“锅盖效应”气态水迁移方程，物理意义明确。

（2）温度对“锅盖效应”气态水迁移通量具有正相关影响，温度的增加会使迁移通量相应增大。

（3）饱和度的增加会使“锅盖效应”气态水迁移通量呈现先增大后减小的规律，与文献中的试验结果较为一致。

图 1 颗粒分布位置图

Figure 1. Schematic diagram of particle arrangement

下载: 全尺寸图片幻灯片

图 2 颗粒间流体的流动路径

Figure 2. Assumed flow paths in soil particles

下载: 全尺寸图片幻灯片

图 3 数值计算模型示意图

Figure 3. Schematic diagram for numerical model

下载: 全尺寸图片幻灯片

图 4 理论值与数值模拟值对比

Figure 4. Comparison between theoretical and numerical results

下载: 全尺寸图片幻灯片

图 5 不同迂曲度模型计算结果对比

Figure 5. Comparison between model predicted results of different tortuosity

下载: 全尺寸图片幻灯片

图 6 不同m对应的迂曲度变化

Figure 6. Influences of variable m on tortuosity

下载: 全尺寸图片幻灯片

图 7 不同θ对应的迂曲度变化

Figure 7. Influences of variable θ on tortuosity

下载: 全尺寸图片幻灯片

表 1 迂曲度公式表

Table 1 Formulas for tortuosity

公式	文献来源	相关参数
$Γ = 1 - P \ln n$ $Γ = 1 - P \ln n$	Comiti等^[4]	P为拟合系数
$Γ = 1 + 0.8 (1 - n)$ $Γ = 1 + 0.8 (1 - n)$	Koponen等^[6]	0.8为拟合参数
$Γ = 1 + a \frac{1 - n}{{(n - n_{c})}^{m}}$ $Γ = 1 + a \frac{1 - n}{{(n - n_{c})}^{m}}$	Koponen等^[7]	a,m为拟合参数,a=0.65,m=0.19,n_c=0.33
$Γ = n^{- β}$ $Γ = n^{- β}$	Mota等^[8]	β为拟合参数,β=0.4
$Γ = \frac{1}{2} [1 + \frac{1}{2} \sqrt{1 - n} + \sqrt{1 - n} \frac{\sqrt{{(\frac{1}{\sqrt{1 - n}} - 1)}^{2} + \frac{1}{4}}}{1 - \sqrt{1 - n}}]$ $Γ = \frac{1}{2} [1 + \frac{1}{2} \sqrt{1 - n} + \sqrt{1 - n} \frac{\sqrt{{(\frac{1}{\sqrt{1 - n}} - 1)}^{2} + \frac{1}{4}}}{1 - \sqrt{1 - n}}]$	Yu等^[10]	无
$Γ = {(\frac{19}{18})}^{\ln n / \ln (8 / 9)}$ $Γ = {(\frac{19}{18})}^{\ln n / \ln (8 / 9)}$	Li等^[11]	无

下载: 导出CSV

表 2 数值计算参数表

Table 2 Inputs for numerical computation

参数	取值
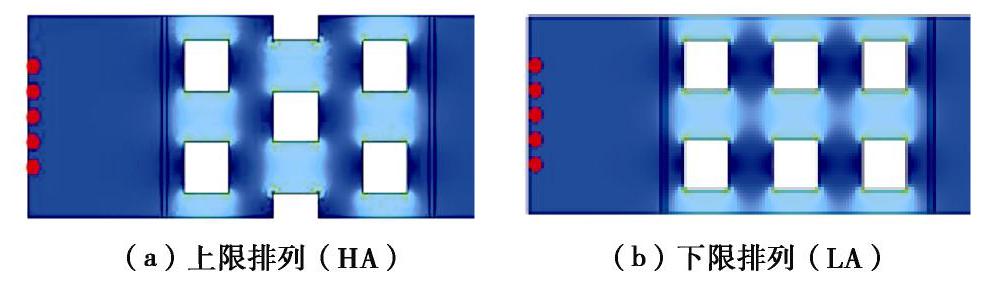
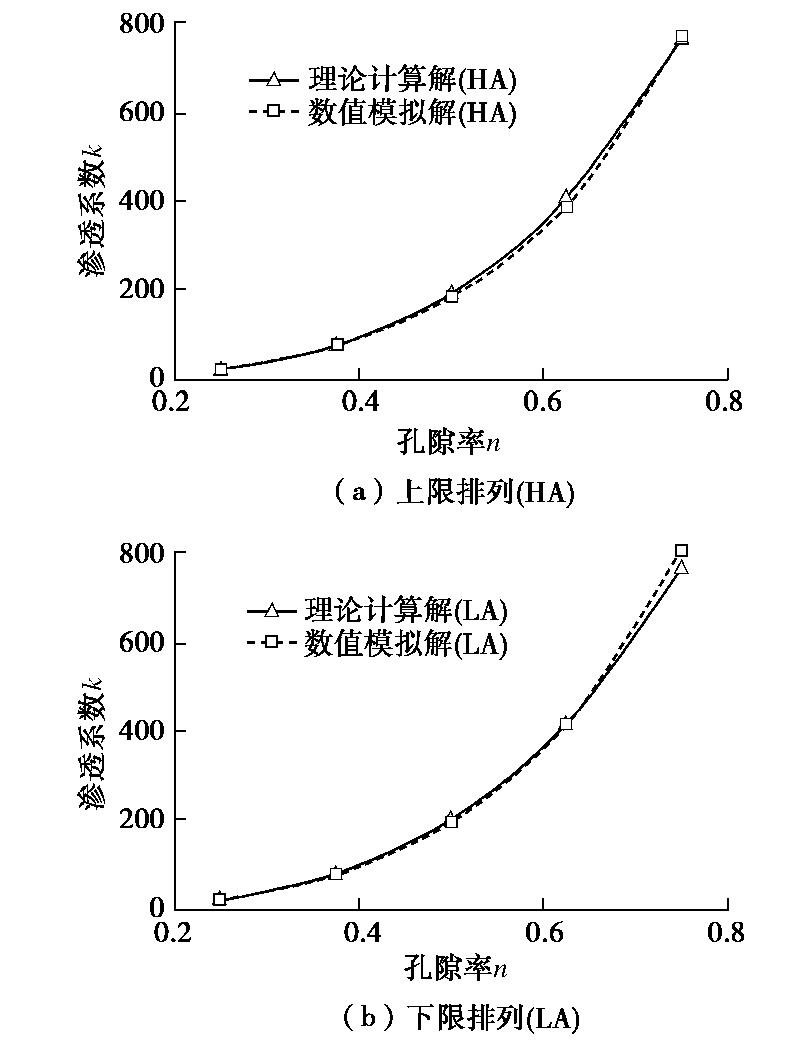
求解方程	$\begin{matrix} ρ \frac{\partial u}{\partial t} + ρ (u \cdot \nabla) u = \nabla \cdot [- p I + μ \nabla u + μ {(\nabla u)}^{T}] + \\ ρ F ρ \nabla \cdot (u) = 0 \end{matrix}$ $\begin{matrix} ρ \frac{\partial u}{\partial t} + ρ (u \cdot \nabla) u = \nabla \cdot [- p I + μ \nabla u + μ {(\nabla u)}^{T}] + \\ ρ F ρ \nabla \cdot (u) = 0 \end{matrix}$
求解方程	黏性不可压缩流体运动方程：ρ为流体密度,u为流速,F为质量力,μ为动力黏度,I为单位张量
流体性质	水
入口压强/Pa	0.1 Pa（保证雷诺数小于5）
入口长度/cm	8
颗粒边长/cm	1.0,1.5,2.0,2.5,3.0
∆l/cm	0.12
雷诺数	小于5

下载: 导出CSV

表 3 理论模型参数取值表

Table 3 Values of parameters in theoretical model

变化参数	取值	其他参数
n	0.4375,对应A=0.03	HA排列：
	0.6094,对应A=0.025	θ= arctan(1/2)
	0.75,对应A=0.02	m=1c=6
	0.8594,对应A=0.015	LA排列：θ=0
	0.9375,对应A=0.01	m=1c=7.6

下载: 导出CSV

参考文献(11)

[1]	员美娟. 多孔介质中流体的若干流动特性研究[D]. 武汉: 华中科技大学, 2008. YUAN Mei-juan. Research on Some Flow Properties of Fluidin Porous Media[D]. Wuhan: Hua Zhong University of Science and Technology, 2008. (in Chinese)
[2]	BROOKS R H, COREY A T. Hydraulic properties of porous media[J]. Hydrol Pap, 1964, 3(1): 352-366.
[3]	SHACKELFORD C D, MOORE S M. Fickian diffusion of radionuclides for engineered containment barriers: diffusion coefficients, porosities, and complicating issues[J]. Engineering Geology, 2013, 152(1): 133-147. doi: 10.1016/j.enggeo.2012.10.014
[4]	COMITI J, RENAUD M. A new model for determining mean structure parameters of fixed beds from pressure drop measurements: application to beds packed with parallelepipedal particles[J]. Chemical Engineering Science, 1989, 44(7): 1539-1545. doi: 10.1016/0009-2509(89)80031-4
[5]	MAURET E, RENAUD M. Transport phenomena in multi-particle systems: I limits of applicability of capillary model in high voidage beds-application to fixed beds of fibers and fluidized beds of spheres[J]. Chemical Engineering Science, 1997, 52(11): 1807-1817. doi: 10.1016/S0009-2509(96)00499-X
[6]	KOPONEN A, KATAJA M, TIMONEN J. Tortuous flow in porous media[J]. Phys Rev E Stat Phys Plasmas Fluids RelatInterdiscip Topics, 1996, 54(1): 406-410.
[7]	KOPONEN A, KATAJA M, TIMONEN J. Permeability and effective porosity of porous media[J]. Phys Rev E, 1997, 56: 3319-3325. doi: 10.1103/PhysRevE.56.3319
[8]	MOTA M. Binary spherical particle mixed beds: Porosity and permeability relationship measurement[J]. Filtration Society, 2001, 1(4): 101-106.
[9]	GHANBARIAN B, HUNT A G, EWING R P, et al. Tortuosity in porous media: a critical review[J]. Soil Science Society of America Journal, 2013, 77(5): 1461-1477. doi: 10.2136/sssaj2012.0435
[10]	YU B M, LI J H. A geometry model for tortuosity of flow path in porous media[J]. Chinese Physics Letters, 2004, 21(8): 1569-1571.
[11]	LI J H, YU B M. Tortuosity of flow paths through a sierpinski carpet[J]. Chinese Physics Letters, 2011, 28(3): 34701-34703. doi: 10.1088/0256-307X/28/3/034701

施引文献(35)

期刊类型引用(19)

1.	彭俊皓，魏玉峰，李常虎，王群，李征征. 基于DBO-GRNN神经网络的冰水堆积物渗透系数预测. 人民长江. 2025(02): 167-174 . 百度学术
2.	张杰，黄勇. 长江漫滩区软土渗透系数计算方法对比分析. 中国煤炭地质. 2024(02): 37-42 . 百度学术
3.	王宇虓，杜广印，刘松玉，杨泳，周同和，徐金涛. 振杆密实法加固粗粒混合土模型试验. 工程科学与技术. 2024(03): 99-108 . 百度学术
4.	樊书抗，杨正权，朱凯斌，赵艺颖，刘小生，赵剑明. 土的级配特征与连续级配方程研究. 水利学报. 2024(05): 597-606 . 百度学术
5.	郭海，张安银. 基于PCA的长江漫滩软弱黏性土渗透特性研究. 江苏建筑. 2024(04): 102-105 . 百度学术
6.	赵桂锋，蒋明杰，张振，王天成，梅国雄. 粗粒土缩尺级配的渗透系数规律试验. 工程科学与技术. 2024(05): 240-246 . 百度学术
7.	李诗琪，杨忠平，刘浩宇，高宇豪，刘新荣. 考虑间断级配影响的土石混合体水力侵蚀分异机理. 土木工程学报. 2024(10): 125-134 . 百度学术
8.	付宏渊，杨海涛，吴二鲁，曾铃，钟涛，姜懿芸. 考虑炭质泥岩颗粒破碎的级配演化预测模型. 水利学报. 2024(09): 1058-1070 . 百度学术
9.	杨锴，杨奇，徐方，徐俏东，韩学良. 考虑细粒含量的单参数连续级配方程研究. 铁道科学与工程学报. 2024(12): 5094-5103 . 百度学术
10.	曲诗章，刘晓明，黎莉，陈仁朋. 基于双分形级配模型参数的粗粒土渗透系数计算公式. 岩土工程学报. 2023(01): 144-152 . 本站查看
11.	侯龙清，袁晓铭，陈龙伟，李明东. 一种新型南55渗透仪研制及工程应用. 岩土工程学报. 2023(02): 419-425 . 本站查看
12.	李浩，李春艳，张嵩，谢英美. 建筑工程中地质特征及岩土工程支护研究. 能源与环保. 2023(01): 181-186 . 百度学术
13.	赵贵章，孔令莹，徐远志，王淑丽，王展. 银川平原典型介质的颗粒级配对渗透系数的影响研究. 中国农村水利水电. 2023(04): 203-207 . 百度学术
14.	张福海，徐嘉成，薛浩宇，刘峥嵘. 级配分布对杂填土地基互嵌沉降影响的试验分析. 河南科学. 2023(05): 730-737 . 百度学术
15.	林玉祥，林浩东，莫品强，褚锋，庄培芝. 基于XGBoost的堆场软土渗透系数反演研究. 西安理工大学学报. 2023(01): 133-140 . 百度学术
16.	袁仕方，曹志翔，韩志洋，张玲洁. 藏东南粗粒土降雨入渗影响因素试验分析. 高原农业. 2022(02): 189-196 . 百度学术
17.	丁林楠，李国英，魏匡民. 描述土体级配分布的级配方程及其适用性. 岩土力学. 2022(S1): 173-183 . 百度学术
18.	段钊，袁林，毕银丽，王凯，吴延斌，张庆. 紫花苜蓿根系-黄土复合体剪切特性与库仑修正模型. 煤田地质与勘探. 2022(12): 85-95 . 百度学术
19.	骆莉莎，周昕，林军. 颗粒形态对粗粒土渗透系数影响的数值模拟研究. 湖南工业职业技术学院学报. 2021(01): 93-96 . 百度学术

其他类型引用(16)

资源附件(0)

图(7) / 表(3)

计量

文章访问数: 327
HTML全文浏览量: 24
PDF下载量: 264
被引次数: 35

0. 引言
1. 一维“锅盖效应”气态水迁移方程
1.1 “锅盖效应”的机理
1.2 一维“锅盖效应”气态水迁移方程的建立
2. 结论

考虑颗粒排列的土体几何迂曲度模型 English Version

作者简介: 颜瀚（1994— ）,男,硕士研究生,主要从事冻土渗流方面的研究工作。E-mail：yanhanxy@csu.edu.cn

通讯作者: 张升, E-mail：zhang-sheng@csu.edu.cn

计量

出版历程