循环扭剪作用下黄土的动剪切特性试验研究

邵帅; 邵生俊; 陈攀; 袁浩

doi:10.11779/CJGE202001019

循环扭剪作用下黄土的动剪切特性试验研究 English Version

邵帅^1,,
邵生俊^{1, 2, ,},
陈攀¹,
袁浩¹

1.
西安理工大学岩土工程研究所,陕西　西安　710048
2.
陕西省黄土力学与工程重点实验室,陕西　西安　710048

基金项目:

国家自然科学基金面上项目 11572245

详细信息

作者简介:
邵帅（1991— ）,男,博士研究生,主要从事黄土力学与土动力学研究。E-mail：315602024 @qq.com

通讯作者:
邵生俊, E-mail：sjshao@xaut.edu.cn

中图分类号: TU43
计量
- 文章访问数: 331
- HTML全文浏览量: 18
- PDF下载量: 150
出版历程
- 收稿日期: 2018-10-05
- 网络出版日期: 2022-12-07
- 刊出日期: 2019-12-31

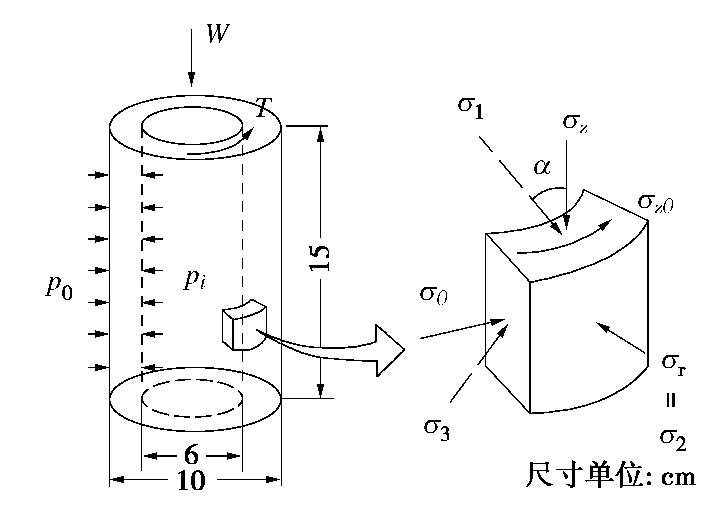
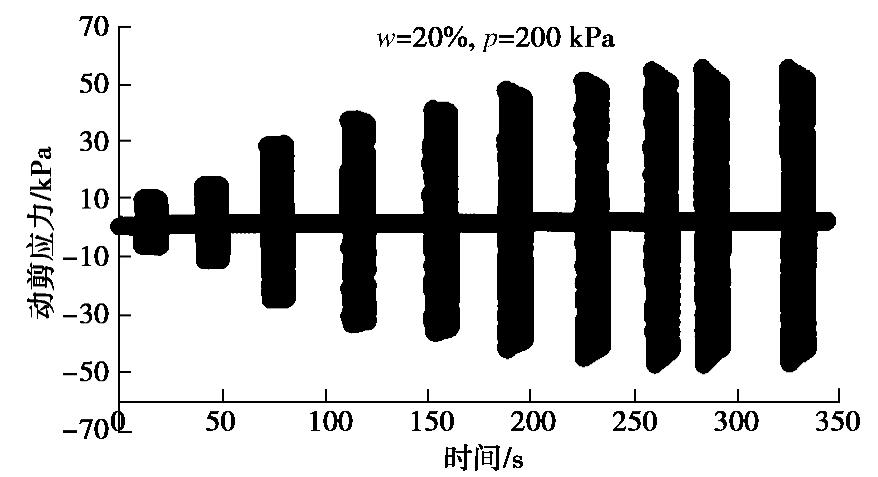
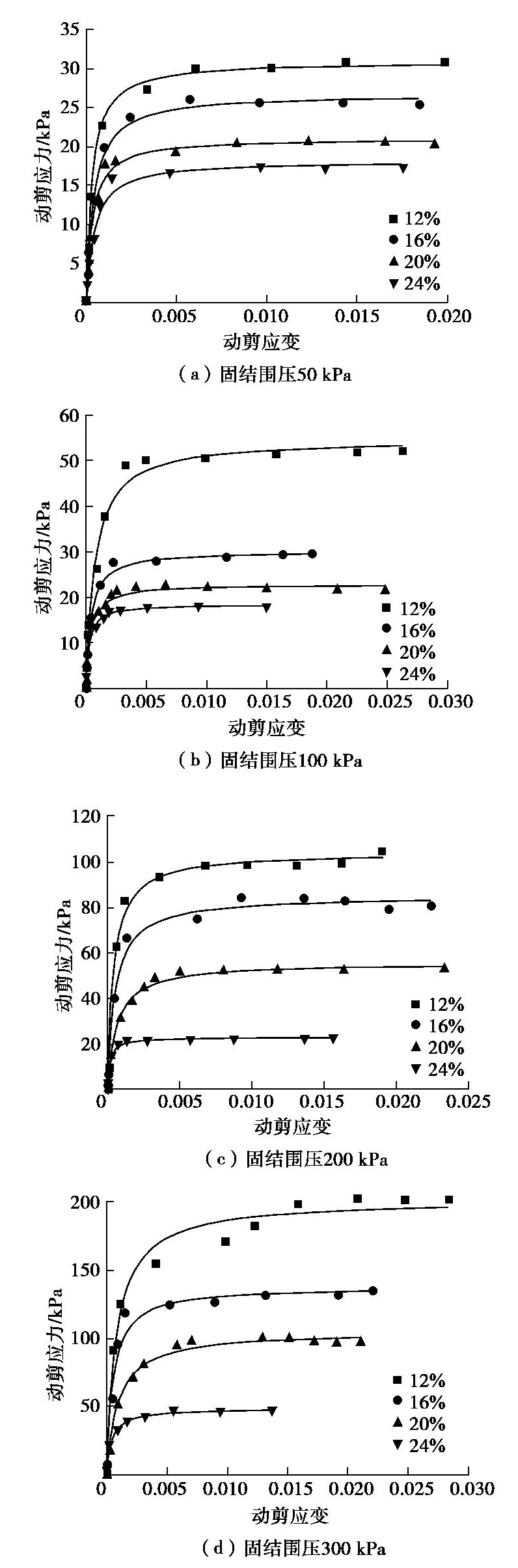
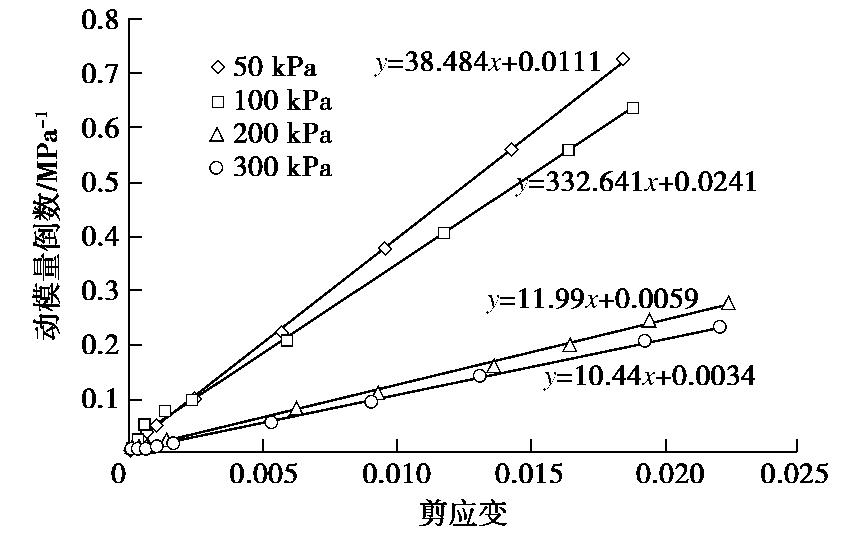
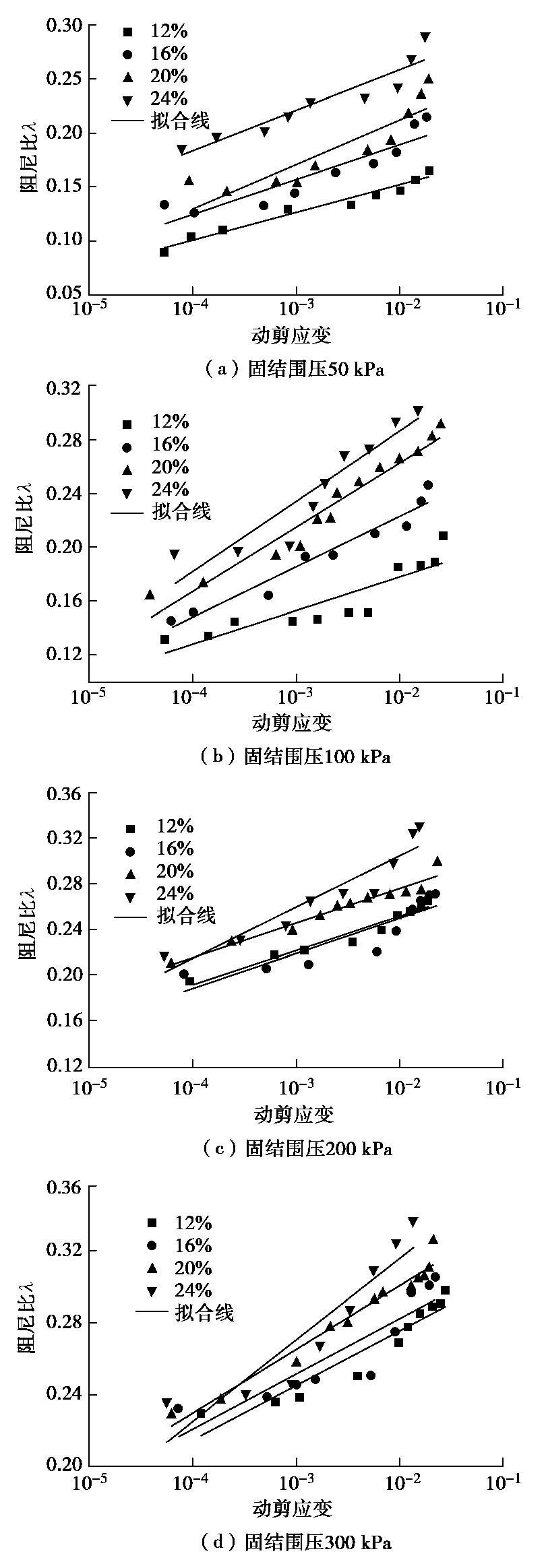
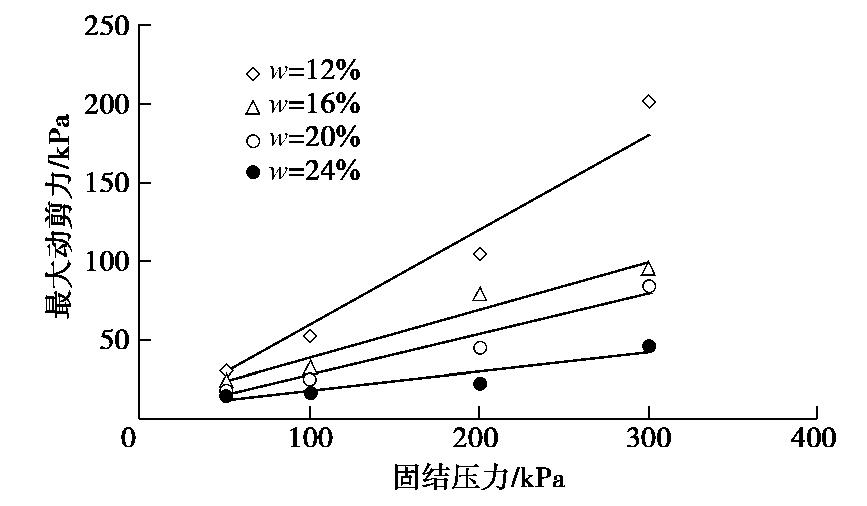
Experimental study on dynamic shear characteristics of loess under cyclic torsional shearing

1.
Institute of Geotechnical Engineering, Xi'an University of Technology, Xi'an 710048, China
2.
Shaanxi Provincial Key Laboratory of Loess Mechanics and Engineering, Xi'an 710048, China

摘要

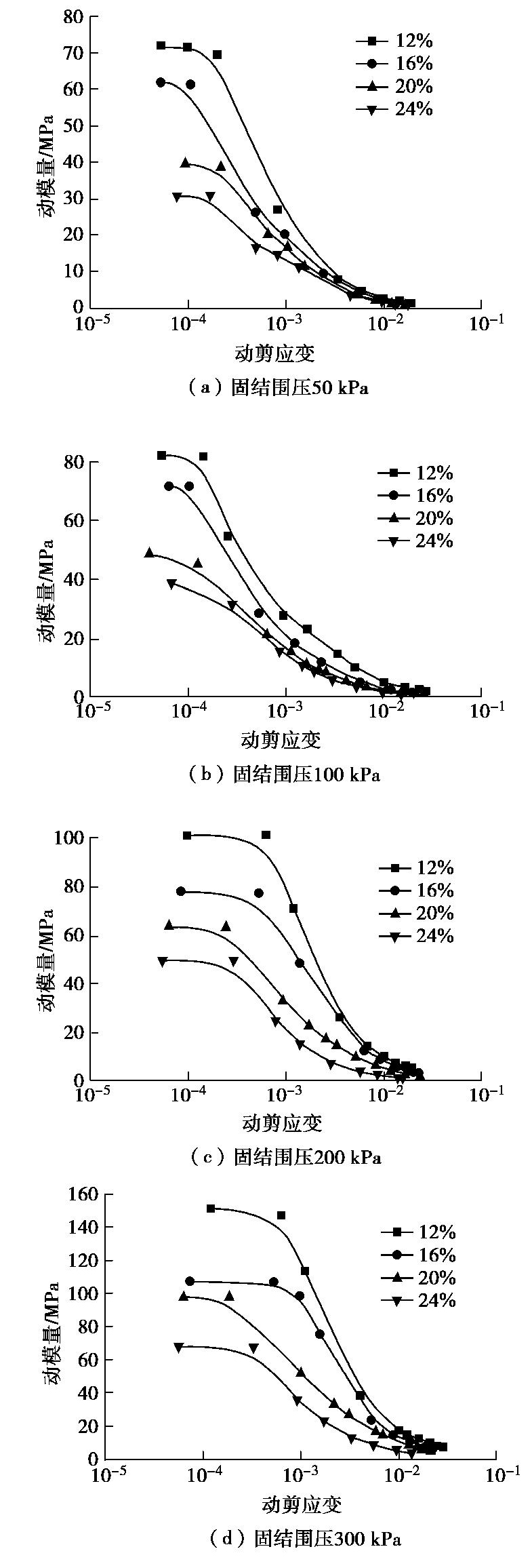
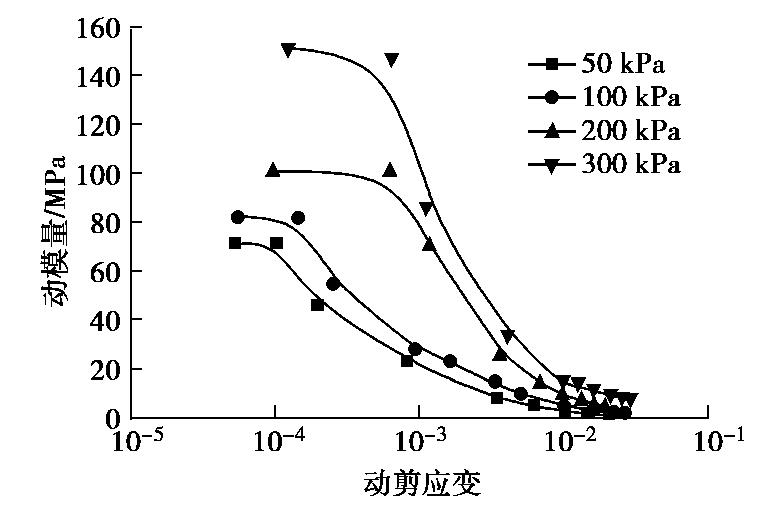
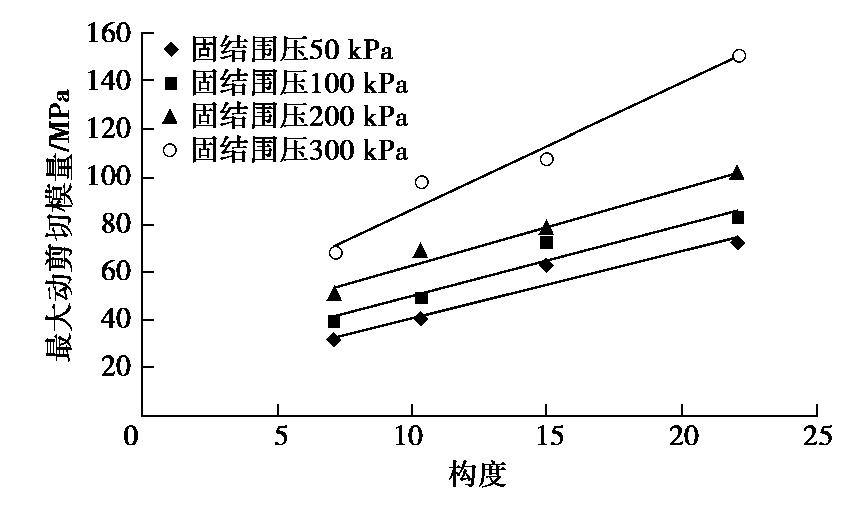
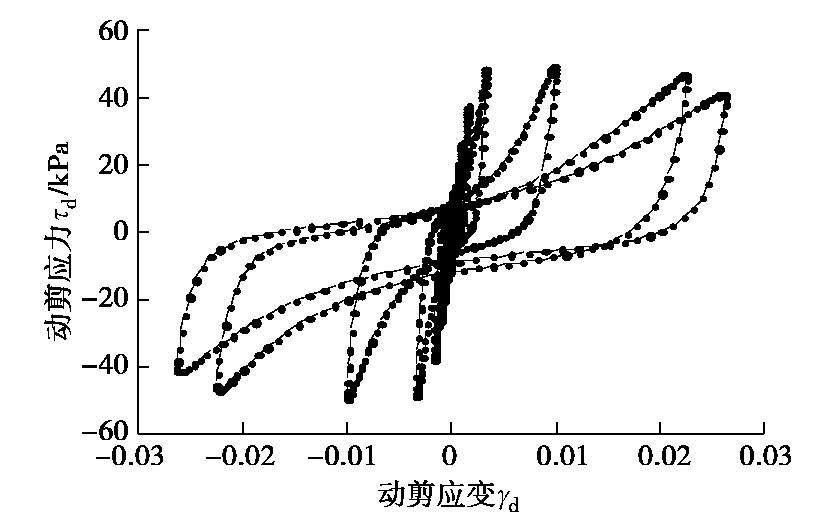
摘要: 原状黄土具有显著的结构性,在增湿及循环剪切作用下均可导致其结构破坏。通过不同固结围压条件下大尺寸原状黄土圆筒试样的动扭剪试验,测试分析了原状黄土从小应变到大应变的动应力应变关系,动剪切模量和阻尼比的变化规律,以及逐级增大循环扭剪作用下黄土的剪切强度。得到了10^-5～10^-2剪切应变范围内黄土动剪切模量随固结围压和含水率的变化规律,分析了黄土最大动剪切模量随黄土构度的变化规律。建立了黄土最大动剪切模量与构度和固结围压的关系式。揭示不同固结围压条件下不同含水率黄土的阻尼比随动剪应变对数值的变化分布在一个带内；循环扭转作用下圆筒黄土样存在两组破坏面。
- 原状黄土 /
- 动扭剪试验 /
- 动应力应变关系 /
- 动剪切模量 /
- 阻尼比 /
- 剪切破坏面
Abstract: The unsaturated intact loess has remarkable structured properties. Its structure is damaged by wetting and cyclic shear action, which leads to the development of shear and subsidence deformation of loess under earthquake. Based on the dynamic torsional shear tests on hollow cylindrical specimens of intact loess under different consolidation pressures, the dynamic shear-strain relationship from small to large strain, the dynamic shear modulus and the dynamic damping ratio of loess are tested and analyzed. The relationships between dynamic shear stress and shear strain, dynamic shear modulus and dynamic damping ratio and the failure strength of loess under gradually increasing cyclic torsion shear action are measured. The variation rules of dynamic shear modulus of loess under different consolidation pressures and moisture contents are obtained in the shear strain range of 10^-5~10^-2. It is shown that the maximum dynamic shear modulus increases with the initial structural index of loess. An approximate linear relationship among the maximum dynamic shear modulus, the structural index and the consolidation pressure is established. The damping ratio of loess changing with the dynamic shear strain logarithm under different consolidation pressure and moisture contents is released. The shear failure characteristics of cylindrical loess samples under cyclic torsional shear action are constituted by two groups of shear failure planes.
- undisturbed loess /
- dynamic torsional shear test /
- dynamic stress-strain relationship /
- dynamic shear modulus /
- damping ratio /
- shear failure plane

HTML全文

0. 引言

近年来,城市轨道交通以其便捷快速的优点在许多城市得到快速的发展。然而随着城市化进程的不断推进,许多已建成的地铁隧道附近不可避免地受到外部工程活动扰动影响,其中突发地表堆载引发的隧道变形事故日益突出^[1],如为便于上海嘉闵高架的施工将河道作为堆放材料场地引起地铁9号线产生较大的不均匀沉降^[2]以及违规弃土引起的地铁正上方堆载导致隧道的横向变形^[3-4]等。地表堆土荷载作用引起的附加应力,会破坏盾构结构原有的平衡状态,引起隧道应力重分布,产生一定的纵向和横向变形,一旦结构内力超过混凝土和螺栓容许应力,会引发管片压损或开裂等^[5],对地铁安全造成严重影响。因此研究地表堆载对临近运营地铁盾构隧道的影响具有重要意义。

目前,已有学者对地表堆载荷载作用下盾构隧道的纵向变形进行了研究。戴宏伟等^[6]利用Boussinesq解和分层总和法计算自由场的位移,基于Euler-Bernoulli梁模型研究了地表施工荷载对临近地铁隧道的影响,但未考虑土体成层特性和隧道自身的结构特性；魏新江等^[7]、魏纲等^[8]基于变分法研究了堆载对下卧隧道错台变形的影响,康成等^[9]采用Timoshenko梁模型研究了不同堆载形式对隧道纵向变形的影响,高继锦等^[10]研究了堆载对下卧交叉隧道竖向位移的影响,但是他们的研究忽略了土体的成层特性；李俊昱等^[11]根据层状弹性半空间理论计算了高填方堆载对地埋管线受力和变形的影响,研究成果虽然涉及到土体的成层特性但没有考虑管线接头的影响。综上,这些研究成果或考虑的土层单一,不能分析土层特性对隧道变形的影响；或忽略了隧道接头引起的隧道整体刚度的弱化,无法准确反映分层地基中堆载对隧道纵向变形的影响。黄大维等^[3]、张明告等^[12]、Zhang等^[13]、张治国等^[14]研究表明当土层性质差别比较大时,不能简单地将分层地基等效为均值地基,关于这一点,康成等^[9]也明确指出。

在实际工程中,由于土是长期自然沉积形成的,因此天然地基并非是均质的弹性体,而是层状分布。基于层状弹性半空间理论^[15-16],本文建立了层状地基中地表堆载对既有隧道影响的弹性分析方法。利用Fourier变换,首先推导了直角坐标系下非均质土体中堆载引起的附加应力；基于两阶段法^[17],采用Timoshenko梁模型和Winkker地基模型,计算地表堆载下隧道的响应；进一步分析上覆土层和下卧土层对隧道内力和变形的影响。与已有的研究成果相比,本文的计算模型可以同时考虑土体的分层特性及隧道的结构特性,通用性更强。

1. 计算模型

1.1 直角坐标系下弹性层状半空间体系基本解

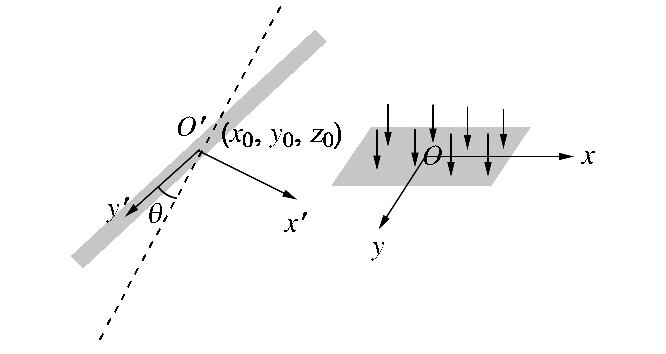
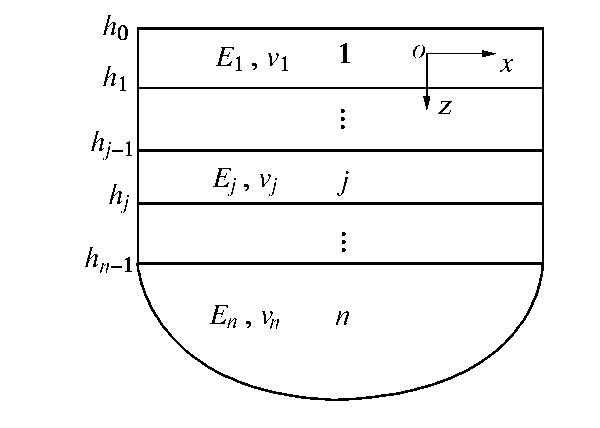
地表堆载作用下将在地层中产生附加应力,从而引起已有地铁隧道产生沉降变形,甚至影响隧道的正常运营。为简化计算,得到堆载下分层地基中的基本解,本文计算模型做如下假定：①地基由多个具有有限厚度的水平层以及半无限空间体组成,每层都是均匀、连续、各向同性的弹性体（如图1所示）；②各层之间弹性接触,且不发生相对滑动；③不考虑土体固结和蠕变以及地表堆载随时间的变化,且堆载前隧道变形已经稳定。

图 1 层状地基示意图

Figure 1. Cross section of multi-layered soils

下载: 全尺寸图片幻灯片

从弹性力学中不计体力的平衡微分方程、几何方程和物理方程构造如下控制方程^[18]：

(1)

式中, $σ_{z}$ , $τ_{z x}$ , $τ_{y z}$ 分别为竖向应力和剪应力, $u_{x}$ , $u_{y}$ , $u_{z}$ 分别为3个方向的位移。

为推导方便,采用如下变换：

$\begin{matrix} χ_{1} = \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y}, Γ_{1} = \frac{\partial u_{x}}{\partial x} + \frac{\partial u_{y}}{\partial y}, χ_{2} = \frac{\partial τ_{x z}}{\partial y} - \frac{\partial τ_{y z}}{\partial x}, \\ Γ_{2} = \frac{\partial u_{x}}{\partial y} - \frac{\partial u_{y}}{\partial x} 。 \end{matrix}$

(2)

双重Fourier变换与逆变换采用如下形式进行：

$\begin{matrix} ({\tilde{χ}}_{1}, {\tilde{Γ}}_{1}, {\tilde{σ}}_{z}, {\tilde{u}}_{z}, {\tilde{χ}}_{2}, {\tilde{Γ}}_{2}) = \frac{1}{4 π^{2}} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} (χ_{1}, Γ_{1}, σ_{z}, u_{z}, χ_{2}, Γ_{2}) \cdot \\ e^{- i (f_{x} x + f_{y} y)} d x d y, \end{matrix}$

(3a)

$\begin{matrix} (χ_{1}, Γ_{1}, σ_{z}, u_{z}, χ_{2}, Γ_{2}) = \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} ({\tilde{χ}}_{1}, {\tilde{Γ}}_{1}, {\tilde{σ}}_{z}, {\tilde{u}}_{z}, {\tilde{χ}}_{2}, {\tilde{Γ}}_{2}) \cdot \\ e^{i (f_{x} x + f_{y} y)} d f_{x} d f_{y} 。 \end{matrix}$

(3b)

$f_{x}$ 和 $f_{y}$ 分别对应于时域中的x和y坐标。结合式（2）,对控制方程（1）进行双重Fourier变换,并写成矩阵形式,有

$\frac{d {\tilde{U}}_{I 1}}{d z} = A_{I 1} {\tilde{U}}_{I 1}$ ,

(4a)

$\frac{d {\tilde{U}}_{I 2}}{d z} = A_{I 2} {\tilde{U}}_{I 2}$ ,

(4b)

式中, $f = \sqrt{f_{x}^{2} + f_{y}^{2}}$ , ${\tilde{U}}_{I 1} = {[\begin{matrix} {\tilde{Γ}}_{1} & {\tilde{u}}_{z} & {\tilde{χ}}_{1} & {\tilde{σ}}_{z} \end{matrix}]}^{T}$ ,

$\begin{array}{l} {\tilde{U}}_{I 2} = {[\begin{matrix} {\tilde{Γ}}_{2} & {\tilde{χ}}_{2} \end{matrix}]}^{T} \\ A_{I 1} = [\begin{matrix} 0 & f^{2} & \frac{2 (1 + μ)}{E} & 0 \\ - \frac{μ}{1 - μ} & 0 & 0 & \frac{(1 + μ) (1 - 2 μ)}{(1 - μ) E} \\ \frac{E}{1 - μ^{2}} f^{2} & 0 & 0 & \frac{1}{1 - μ^{2}} f^{2} \\ 0 & 0 & - 1 & 0 \end{matrix}], \\ A_{I 2} = [\begin{matrix} 0 & \frac{2 (1 + μ)}{E} \\ \frac{E}{2 (1 + μ)} f^{2} \end{matrix}] 。 \end{array}$

依据Cayley-Hamilton定理,对矩阵方程式（4a）,（4b）进行求解可以得到单层地基中应力和位移的传递函数,传递函数的具体表达形式参见文献[18],由于篇幅限制,本文不再赘述。采用与文献[16]相似的处理方式,就可以得到堆载作用下层状土体的应力位移关系：

(5)

基于文献[19]的方法,对式（5）进行双重Fourier逆变换,可以得到真实空间域中地表堆载引起的附加应力数值解。

对于如图2所示的地面偏心堆载,采用如式（6）的坐标变换,并代入式（5）中,即可以得到偏心荷载下分层地基中应力和位移的响应。

$\begin{array}{l} x = x^{'} \cos θ - y^{'} \sin θ + x_{0}, \\ y = x^{'} \sin θ + y^{'} \cos θ + y_{0}, \\ z = z_{0} 。 \end{array}}$

(6)

图 2 偏心堆载

Figure 2. Eccentric surcharge

下载: 全尺寸图片幻灯片

1.2 地表荷载作用下盾构隧道变形计算

通过1.1节可以得到地表堆载下分层地基中任一深度处附加应力的计算结果,接下来采用两阶段法^[17],计算地铁隧道与土体的相互作用,分析地表堆载下隧道的纵向变形响应。

（1）土体模型

在结构与土体的相互作用计算中,通常采用Winkler地基模型^{[17, 20]}、Pasternak地基模型^[21]、连续弹性体模型来模拟软土^[13]。Liang等^[21-22]分析了基坑开挖对下卧地铁的影响,土体分别采用Winkler地基模型和Pasternak地基模型进行模拟,研究表明两种地基模型下得到的隧道隆起量差别不大,但Winkler地基模型更方便于工程应用。因此,本文土体模型采用Winkler地基模型。关于地基反力系数,Vesic基于地表弹性地基梁,给出了确定地基反力系数的经验公式。由于没有考虑土层埋深对土层刚度的影响,Vesic经验公式会高估了隧道的变形。为了更好地反映埋深对土层刚度的影响,Liang等^[21]提出了基于埋深修正的Vesic地基反力系数经验公式：

$k = \frac{1.3 E_{s}}{η B (1 - μ^{2})} \sqrt[12]{\frac{E_{s} B^{4}}{E I}},$

(7)

式中, $η = 1 + \frac{1}{1.7 z_{0} / B}$ ^[20], $E_{s}$ , $μ$ 分别为隧道周围土体变形模量和泊松比,B为隧道外径, $E I$ 取隧道等效抗弯刚度 $E I_{eq}$ 。

（2）隧道模型

城市地铁隧道通常由预制管片组成,管片与管片之间通过高强螺栓连成一个整体。毫无疑问,管片接头的存在会削弱盾构隧道的整体刚度。大量监测数据表明,隧道沿轴线方向的变形可以分解为两部分：①弯曲引发管片的弯曲变形,造成管片的张开；②不均匀沉降诱发的剪切应力引发管片之间的错台变形^[23-24]。戴宏伟等^[6]、李俊昱等^[11]采用Euler-Bernoulli梁分别计算了隧道和管线的纵向变形,但Euler-Bernoulli梁只能考虑弯曲变形,无法得到管片之间的错台量大小,因此本文采用Timoshenko梁来模拟盾构隧道。

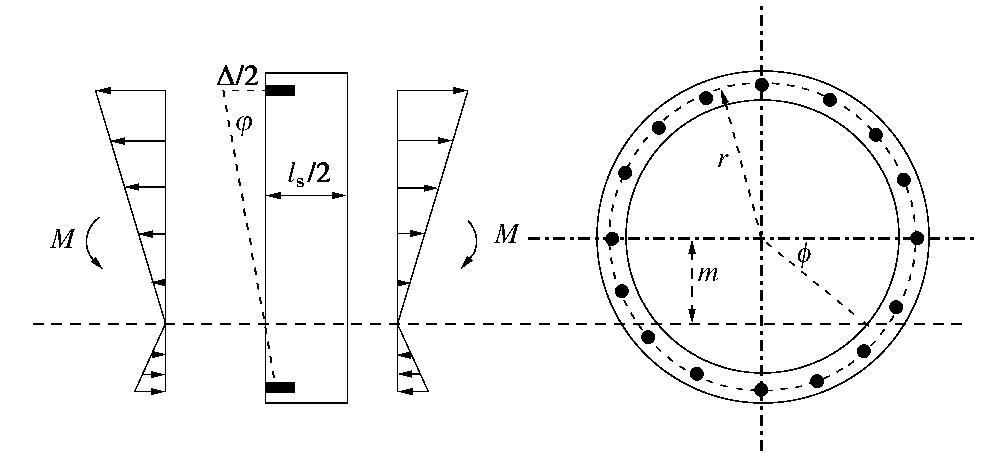
为了考虑管片之间接头的存在引起隧道纵向刚度的衰减,大量学者进行了研究^[25-26],其中日本学者Shiba提出的刚度等效方法在工程中得到了大量应用,本文同样也采用该方法。图3为隧道变形示意图,通过变形协调条件,可以得到隧道等效抗弯刚度、等效抗剪刚度、张开量和错台量。

图 3 管片受力和变形示意图

Figure 3. Deformation and stress of linings

下载: 全尺寸图片幻灯片

a）等效抗弯刚度和张开量

$\begin{array}{l} ϕ + \cot ϕ = π (0.5 + \frac{N k_{b} l_{s}}{E_{c} A_{c}}), \\ φ = \frac{l_{s}}{E_{c} I_{c}} \frac{\cos ϕ + (ϕ + π / 2) \sin ϕ}{\cos^{3} ϕ} M, \\ E I_{eq} = \frac{\cos^{3} ϕ}{\cos ϕ + (ϕ + π / 2) \sin ϕ} E_{c} I_{c} 。 \end{array}}$

(8)

式中,N为纵向螺栓的数量, $k_{b}$ 为螺栓的刚度： $k_{b} =$ $E_{b} A_{b} / l_{b}$ , $l_{s}$ 和 $l_{b}$ 分别为管片和螺栓的长度, $E_{c}$ 和 $I_{c}$ 分别为管片的弹性模量和隧道的惯性矩。

由弯矩引起管片之间最大张开量可以表示为

$Δ = φ (r + m) = \frac{M}{E I_{eq}} (r + r \sin ϕ) l_{b} 。$

(9)

b）等效剪切刚度和错台量

基于Timoshenko梁理论和变形协调条件,隧道的等效剪切刚度可以表示为

$G_{e q} = ζ \frac{l_{s}}{\frac{l_{b}}{N κ_{b} G_{b} A_{b}} + \frac{l_{s}}{κ_{c} G_{c} A_{c}}},$

(10)

式中 $ζ$ 为考虑影响隧道刚度相关因素的修正参数,一般取1； $κ_{b}$ 和 $κ_{c}$ 为Timoshenko梁和管片的剪切刚度修正系数,分别取0.9和0.5； $G_{b}$ 和 $G_{c}$ 分别为螺栓和隧道的剪切模量； $A_{b}$ 和 $A_{c}$ 分别为螺栓和隧道的横截面积。

由剪切引起管片之间的错台量可以表示为

$δ = l_{s} \frac{Q}{G_{eq}} 。$

(11)

（3）隧道变形计算模型

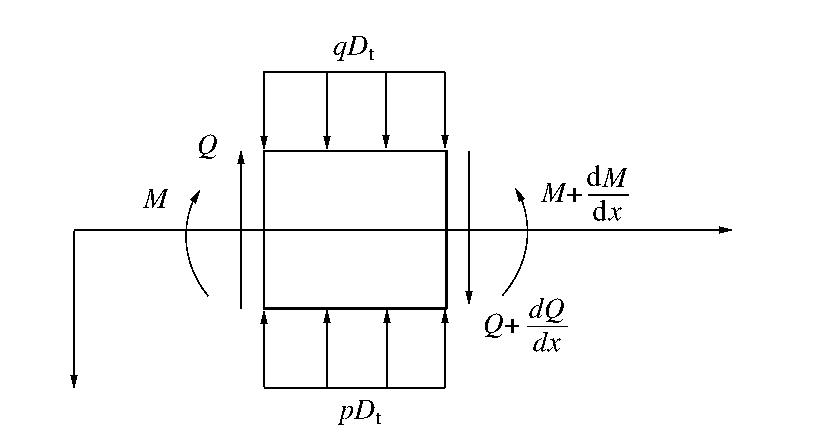
为简化计算,假设地表荷载作用前隧道变形已经稳定、隧道与周围土体始终保持接触,并且不考虑土体固结、蠕变以及荷载随时间的变化。取隧道微元体单元进行受力分析（如图4所示）,可以得到如下两个平衡方程：

图 4 隧道单元受力分析图

Figure 4. Force analysis of element

下载: 全尺寸图片幻灯片

$Q + p D_{t} d x = q D_{t} d x + Q + d Q / d x （力平衡方程）,$

(12a)

$\begin{matrix} - M - Q d x - p D_{t} d x d x / 2 + q D_{t} d x d x / 2 + M + d M / d x = 0 \\ （力矩平衡方程）。 \end{matrix}$

(12b)

式中 $Q$ 和 $M$ 分别为作用在隧道上的剪力和弯矩； $q$ 为堆载引起的附加应力； $D_{t}$ 为隧道外径； $p$ 为地基反力,根据Winkler地基模型, $p = k w (x)$ , $k$ 为地基反力系数,由式（7）确定, $w (x)$ 为堆载引起的隧道沉降。

根据Timoshenko梁理论,内力与变形之间的关系为

$M = - E I_{eq} \frac{d θ}{d x}, Q = G_{eq} (\frac{d w}{d x} - θ),$

(13)

式中, $θ$ 为梁截面中性面的转动角度。

联立式（12a）,（12b）,（13）,可以得到地表竖向荷载下盾构隧道竖向位移w(x)的微分控制方程：

$\frac{d^{4} w (x)}{d x^{4}} + α \frac{d^{2} w (x)}{d x^{2}} + β w (x) = α_{1} \frac{d^{2} q (x)}{d x^{2}} + β_{1} q (x),$

(14)

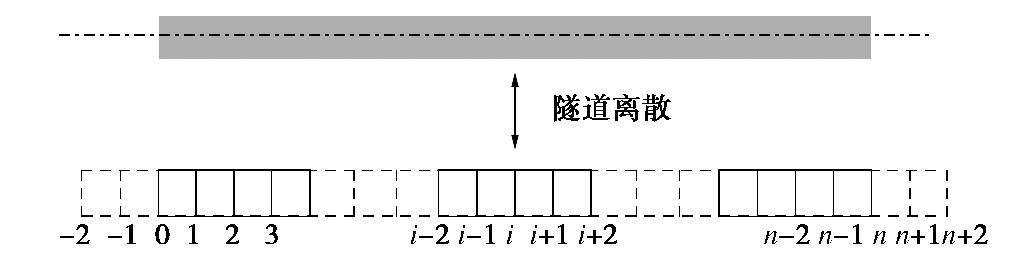
式中, $α = - \frac{k D_{t}}{G_{eq}}$ , $β = \frac{k D_{t}}{E I_{eq}}$ , $α_{1} = - \frac{D_{t}}{G_{eq}}$ , $β_{1} = \frac{D_{t}}{E I_{eq}}$ 。

式（14）为4阶常微分方程,很难直接得到其显式解析解,故采用有限差分法将微分方程转换为代数形式的差分方程,通过编程求其数值解。先将隧道离散成n+5个微单元体,每个单元体的长度为l,如图5所示,-2,-1,n+1和n+2均为虚节点。假设隧道两端均自由,即无弯矩和剪力作用。因此,对于0节点和n节点,分别满足边界条件： $Q_{0} = Q_{n} = 0$ , $M_{0} =$ $M_{n} = 0$ 。根据差分原理,结合边界条件,式（14）可以改写为以挠度w(x)为未知数的矩阵表达式：

图 5 隧道离散分析

Figure 5. Discretization of tunnel

下载: 全尺寸图片幻灯片

$K W = D S,$

(15)

式中, $W = {[w_{0} w_{1} \dots w_{n - 1} w_{n}]}^{T}$ , $S =$ ${[q_{0} q_{1} \dots q_{n - 1} q_{n}]}^{T}$ ,可以通过式（5）求得,K和D的表示形式见附录。求解式（15）就可以得到地表荷载作用下隧道的纵向变形,然后联立式（9）～（13）,进一步可以得到隧道承受的弯矩、剪力、张开量和错台量。

1.3 算例验证

（1）与Boussinesq解比较

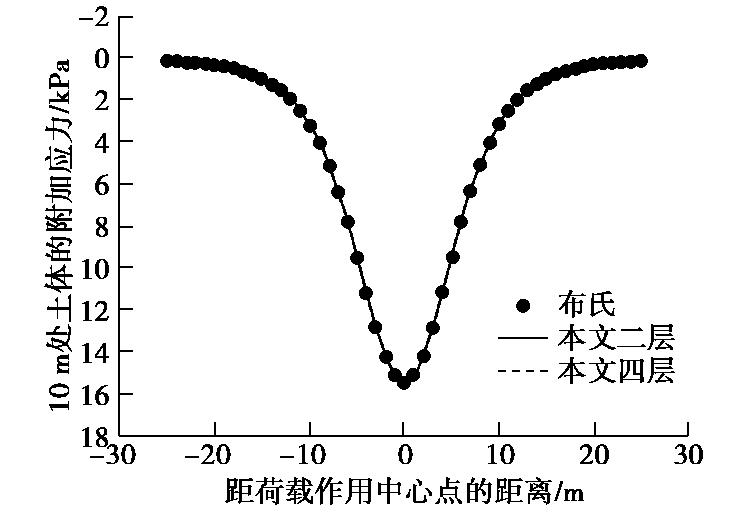
基于式（5）,采用双重Fourier逆变换和高斯积分法,可以得到分层地基中地表堆载引起的附加应力,通过与经典的Boussinesq解进行对比,来验证分层地基应力计算模型以及数值变换的正确性。假设地表作用100 kN的荷载,荷载作用范围为4×10 m,地基土为弹性半空间无限体,弹性模量为10 MPa,泊松比为0.33。分别采用Boussinesq解和本文解（其中土体分层数取为2层和4层）计算10 m处的附加应力,计算结果如图6所示,对比结果表明,本文计算结果与Boussinesq解基本一致,从而验证了本文分层土体附加应力计算模型的可靠性。

图 6 附加应力计算结果对比

Figure 6. Comparison of additional stress

下载: 全尺寸图片幻灯片

（2）与已有文献比较

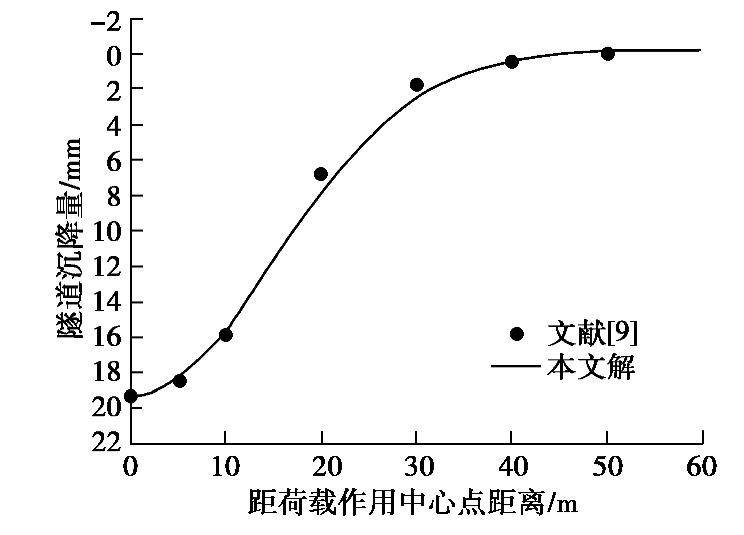
文献[9]以上海典型隧道为研究背景,分析了均质土体中地表堆载对隧道纵向变形的影响。采用本文的计算结果与文献的结果如图7所示,进一步验证了本文计算模型的正确性。

图 7 均质地基中堆载引起的隧道沉降

Figure 7. Comparison of settlement

下载: 全尺寸图片幻灯片

2. 影响参数分析

假定在隧道轴线正上方地表进行工程堆土,堆土重度为18 kN/m³,堆土高度为4 m,地表附加荷载作用范围为2a×2b=20 m×40 m,隧道轴线埋深为15 m。隧道为上海典型地铁隧道,管片内外径分别为5.5 m和6.2 m,环宽为1.2 m,弹性模量为3.45×10⁷ kPa。螺栓为17个,直径为0.03 m,长度为0.4 m,弹性模量为2.06×10⁸ kPa。在下面分析中,若无特别说明,隧道所取参数不变。

2.1 上覆土体模量

为了便于分析,假设第一层层厚10 m,弹性模量变化范围为5～40 MPa,泊松比为0.35,第二层为半无限空间体,弹性模量为10 MPa,泊松比为0.35。

隧道正上方堆载情况下,上覆土体模量对隧道纵向变形影响如图8（a）所示。隧道竖向沉降最大值出现在荷载作用中心处,随着上覆土体模量越大隧道纵向变形越小；当上覆土体模量从5 MPa增大到40 MPa时,隧道最大沉降从16 mm减小为12 mm,最大沉降幅度减小了25%。这主要是因为上覆土体模量越大,土体强度越高,应力扩散效应越明显,作用在隧道上的附加应力也就越小,从而引起隧道的沉降量也就越小。距堆载中心40 m附近,隧道沉降几乎为零,因此隧道沉降槽宽度约为80 m,是荷载作用宽度（沿隧道轴线方向）的4倍,且沉降槽宽度几乎不受上覆土体模量的影响。

图 8 上覆土体模量对隧道内力和变形的影响

Figure 8. Effects of modulus of overlying soil on tunnel deformation and internal forces

下载: 全尺寸图片幻灯片

图8（b）,（c）分别为隧道所受弯矩和张开量随上覆土层模量的变化情况。由图可知,堆载作用下隧道弯矩和张开量沿隧道纵向的分布一致,最大值均出现在荷载作用中心点处,此处即为隧道最危险截面,隧道管片可能因为过大的压应力或拉应力导致破损或产生裂缝,从而引发隧道渗水,影响隧道安全运营。地表堆载下,隧道受到的最大剪力和错台量出现在荷载作用边缘处,如图8（d）,（e）所示,这表明在这些隧道截面处,螺栓承受的剪应力最大,因而最容易发生破坏。

综上,在堆载中心处和边缘处,隧道会因承受较大的弯矩和剪力而出现较大的张开量和错台量,情况严重时甚至导致隧道出现道床脱落管片混凝土挤碎、螺栓剪断、渗漏水以及纵缝张开等^[1]病害,影响隧道的安全运营。所以,一旦隧道正上方出现堆载,需要加强这些隧道截面的监测工作或提前采取保护措施,预防隧道病害的产生。

2.2 下卧土体模量

为了便于分析,假设第一层层厚20 m,弹性模量为10 MPa,泊松比为0.35,第二层为半无限空间体,弹性模量变化范围为5～40 MPa,泊松比为0.35。

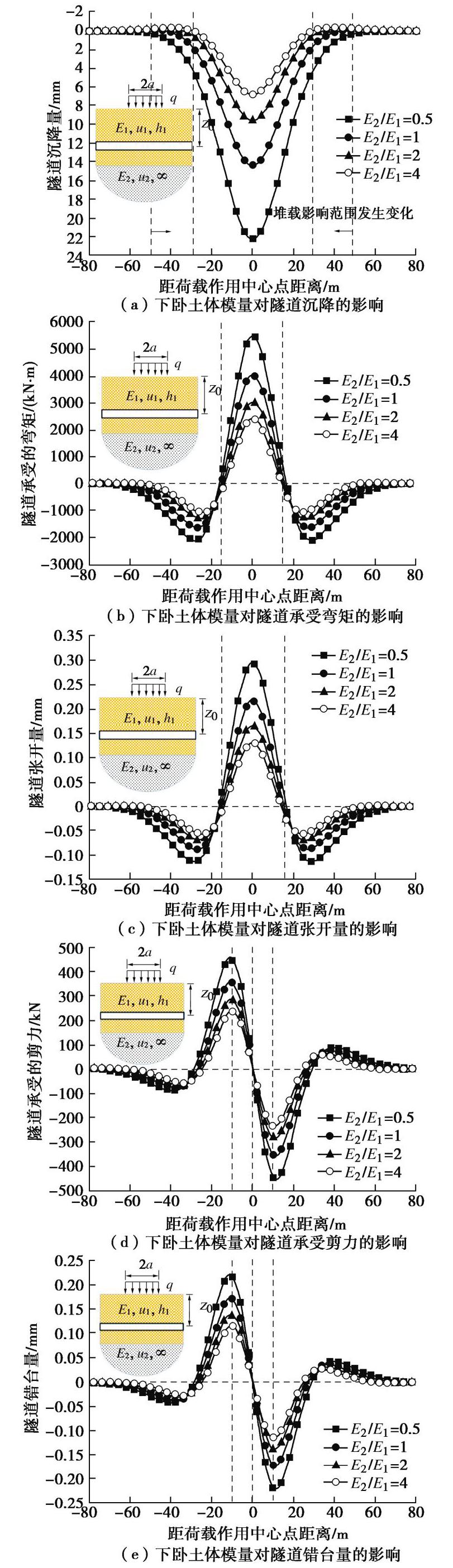
隧道正上方地表堆载作用下,隧道下卧土体模量对隧道内力和变形的影响如图9所示。由图9（a）可知,下卧土体模量越大,地表荷载作用下隧道沉降越小；当下卧土体模量从5 MPa增大到40 MPa时,隧道最大沉降从22 mm减小为7 mm,最大沉降幅度减小了68%。这主要是因为下卧土体模量越大,土体刚度也就越大,对上覆土体的约束作用也随之增加；当下卧土体的模量趋于无穷大时,下卧土层可以等效为刚性边界,即上覆土体底部的竖向位移完全被约束,此种情况下隧道的纵向变形完全取决于上层土体的性质。此外,与图9（a）比较,隧道沉降范围随着下卧土体模量的增大明显缩小,从5倍加载宽度减小为3倍。

图 9 下卧土体模量对隧道内力和变形的影响

Figure 9. Effects of modulus of underlying soil on tunnel deformation and internal forces

下载: 全尺寸图片幻灯片

下卧土体模量对隧道承受的弯矩、张开量、剪力以及错台量的影响分别如图9（b）～（e）所示,随着下卧土体模量的增加,隧道内力和变形随之减小,变化趋势与上层土体一致,此处不再赘述。

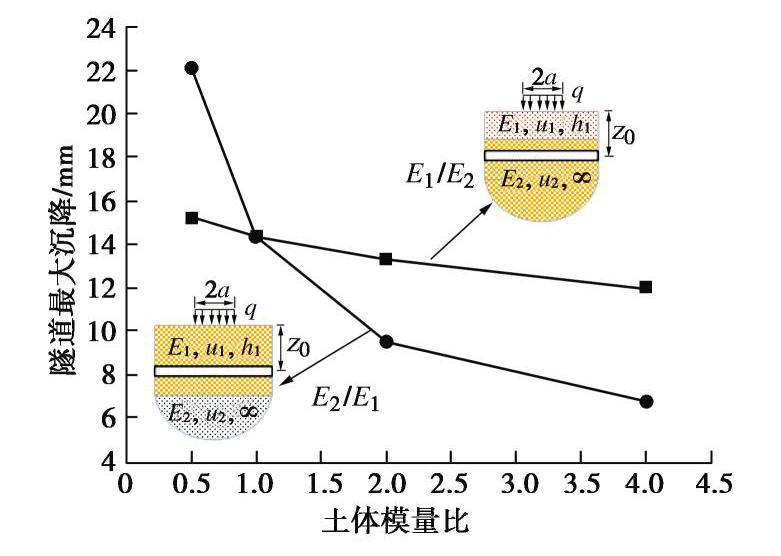
两层土体情况下,隧道最大沉降随土体模量比变化的计算结果如图10所示。由图10可知,在地表堆载作用下,无论是上覆土体模量增加,还是下卧土体模量增加,隧道竖向最大沉降均会降低,相比而言下卧土层的影响更为明显,说明下卧土层控制隧道沉降的效果要优于硬表层地基的情况。另一方面,当下卧土层模量小于隧道所处土层的模量时（即下卧软土层）,隧道沉降急剧增大。因此,若隧道下卧软土层,需要引起重视,不宜进行堆土工程,避免隧道因堆载出现过大的变形。

图 10 最大沉降随土体模量比的变化趋势

Figure 10. Effects of relative soil modulus on maximum tunnel settlement

下载: 全尺寸图片幻灯片

3. 结论

地表堆载会改变隧道原有的平衡状态,引起隧道结构产生过大变形,诱发一系列的隧道病害。基于层状弹性半空间理论,本文建立了层状地基中地表堆载对既有隧道影响的弹性分析方法,分析了土体分层特性对隧道结构响应的影响,得到以下3点结论。

（1）本文采用弹性层状半空间地基模型,建立了能够考虑非均质土体条件的地表大面积荷载对临近既有隧道影响的弹性分析方法,并编写了层状地基中隧道性状的分析程序,方便求解出地表堆载作用下土体特性对既有盾构隧道的内力和变形响应。通过与已有文献数据的对比,验证了本文模型的合理性。

（2）本文方法具有较强的通用性,不仅可以解答均质地基的情况,还可以解答非均质地基的情况,继而可以反映土体分层特性对隧道的影响。对上海典型地铁隧道性状进行参数分析,结果表明上覆土层和下卧土层的弹性模量对隧道沉降和受力具有较为明显的影响,其中增大下卧层土体弹性模量可以显著减小隧道沉降。

（3）当隧道下卧软土层时,地表堆载作用下隧道更容易发生变形,为了保证隧道的安全运营,应该严格评估隧道地表堆载的影响。

此外,限于篇幅,本文仅考虑了隧道正上方大面积堆载引发的隧道纵向变形响应,未涉及到隧道堆载（尤其是偏载）对隧道侧向变形的影响,因此在后续的研究中也可以进行具体分析。

附录

图 1 原状黄土圆筒状试样

Figure 1. Cylindrical sample of loess

下载: 全尺寸图片幻灯片

图 2 圆筒试样扭转加载和应力条件

Figure 2. Loading and stress conditions of specimen in dynamic hollow cylinder torsion test

下载: 全尺寸图片幻灯片

图 3 逐级加荷时程曲线

Figure 3. Time-history curves of step-loading

下载: 全尺寸图片幻灯片

图 4 不同含水率的动剪应力应变曲线

Figure 4. Dynamic shear stress-strain curves under different moisture contents

下载: 全尺寸图片幻灯片

图 5 不同固结围压黄土的动剪应力应变曲线（含水率12%）

Figure 5. dynamic shear stress-strain curves under different consolidation confining pressures at moisture content of 12%

下载: 全尺寸图片幻灯片

图 6 黄土的动模量倒数与动剪应变关系（含水率16%）

Figure 6. Relationship between dynamic modulus reciprocal and dynamic shear strain of loess (moisture content of 16%)

下载: 全尺寸图片幻灯片

图 7 不同含水率黄土的动剪切模量-动剪应变曲线

Figure 7. Dynamic shear modulus-dynamic shear strain relationship curves under different moisture contents

下载: 全尺寸图片幻灯片

图 8 不同围压黄土的动剪切模量-剪应变曲线（含水率12%）

Figure 8. Dynamic shear modulus-shear strain curves of loess under different consolidation pressures (moisture content 12%)

下载: 全尺寸图片幻灯片

图 9 最大动剪切模量随构度的变化

Figure 9. Variation of maximum dynamic shear modulus with structural index

下载: 全尺寸图片幻灯片

图 10 最大动剪切模量与固结围压和构度的关系

Figure 10. Variation of maximum dynamic shear modulus with consolidation confining pressure and structural index

下载: 全尺寸图片幻灯片

图 11 w=12%,围压100 kPa应力应变滞回圈形态图

Figure 11. Stress-strain hysteresis loop patterns

下载: 全尺寸图片幻灯片

图 12 不同含水率的黄土阻尼比变化规律

Figure 12. Variation laws of damping ratio of loess with different moisture contents

下载: 全尺寸图片幻灯片

图 13 黄土的循环扭剪强度

Figure 13. Cyclic torsional shear strengths of loess

下载: 全尺寸图片幻灯片

图 14 圆筒土体扭剪破坏模式

Figure 14. Torsional shear failure modes of cylindrical soils

下载: 全尺寸图片幻灯片

表 1 黄土的基本物理性质指标

Table 1 Basic physical properties of loess samples

天然密度/(g·cm^-3) 含水率/% 干密度/(g·cm^-3) 液限/% 塑限/% 塑性指数

1.68 21.0 1.39 34.2 18.6 15.6

下载: 导出CSV

参考文献(12)

[1]	张振中. 黄土地震灾害预测[M]. 北京: 地震出版社, 1999. ZHANG Zhen-zhong. Earthquake Disaster Prediction of Loess[M]. Beijing: earthquake Press, 1999. (in Chinese)
[2]	王兰民. 黄土动力学[M]. 北京: 地震出版社, 2003. WANG Lan-min. Loess Dynamics[M]. Beijing: Earthquake Publishing House, 2003. (in Chinese)
[3]	陈永明, 石玉成. 中国西北黄土地区地震滑坡基本特征[J]. 地震研究, 2006, 29(3): 276-280. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYJ200603012.htm CHEN Yong-ming, SHI Yu-cheng. Basic characteristics of earthquake landslide in the Loess region of Northwest China[J]. Journal of Seismological Research, 2006, 29(3): 276-280. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZYJ200603012.htm
[4]	潘华, 陈国兴. 动态围压下空心圆柱扭剪仪模拟主应力轴旋转应力路径能力分析[J]. 岩土力学, 2011, 32(6): 1701-1712. PAN Hua, CHEN Guo-xing. Analysis of capabilities of HCA to simulate stress paths for principal stressrotation under dynamic confining pressure[J]. Rock and Soil Mechanics, 2011, 32(6): 1701-1712. (in Chinese)
[5]	沈扬, 周健, 龚晓南. 空心圆柱仪(HCA)模拟恒定围压下主应力轴循环旋转应力路径能力分析[J]. 岩土工程学报, 2006, 28(3): 281-287. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200603001.htm SHEN Yang, ZHOU Jian, GONG Xiao-nan. Analysis on ability of HCA to imitate cyclic principal stress rotation under constant confining pressure[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 281-287. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200603001.htm
[6]	YOSHIMINE M, ISHIHARA K, VARGAS W. Effects of principal stress direction and intermediate principal stress on undrained shear behavior of sand[J]. Soils and Foundations, 1998, 38(3): 179-188. doi: 10.3208/sandf.38.3_179
[7]	SIVATHAYALAN S, VAID Y P. Influence of generalized initial state and principal stress rotation on the undrained response sands[J]. Canadian Geotechnical Journal, 2002, 39: 63-76. doi: 10.1139/t01-078
[8]	ZDRAVKOVIC L, JARDINE R J. The effect on anisotropy of rotationg the principal stress axes during consolidation[J]. Geotechnique, 2001, 51(1): 69-83. doi: 10.1680/geot.2001.51.1.69
[9]	杨利国. 复杂初始应力条件下压实黄土动力特性的试验研究[D]. 杨凌: 西北农林科技大学, 2010. YANG Li-guo. Experimental Study on Dynamic Characteristics of Compacted Loess under Complex Initial Stress[D]. Yangling: Northwest University of Agriculture and Forestry Science and Technology, 2010. (in Chinese)
[10]	王志杰, 骆亚生, 王瑞瑞, 等. 不同地区原状黄土动剪切模量与阻尼比试验研究[J]. 岩土工程学报, 2010, 28(9): 1464-1469. WANG Zhi-jie, LUO Ya-sheng, WANG Rui-rui, et al. Experimental study on dynamic shear modulus and damping ratio ofundisturbed loess in different regions[J]. Chinese Journal of Geotechnical Engineering, 2010, 28(9): 1464-1469. (in Chinese)
[11]	骆亚生, 田堪良. 非饱和黄土的动剪模量与阻尼比[J]. 水利学报, 2005, 36(7): 830-34. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200507010.htm LUO Ya-sheng, TIAN Kan-liang. Dynamic shear modulus and damping ratio of unsaturated loess[J]. Journal of Hydraulic Engineering, 2005, 36(7): 830-34. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200507010.htm
[12]	邵生俊, 王丽琴, 邵帅, 等. 黄土的结构屈服及湿陷变形的分析[J]. 岩土工程学报, 2017, 39(8): 1357-1365. SHAO Sheng-jun, WANG Li-qin, SHAO Shuai, et al. Structural yield and collapse deformation of loess[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(8): 1357-1365. (in Chinese)

施引文献(35)

期刊类型引用(19)

1.	彭俊皓，魏玉峰，李常虎，王群，李征征. 基于DBO-GRNN神经网络的冰水堆积物渗透系数预测. 人民长江. 2025(02): 167-174 . 百度学术
2.	张杰，黄勇. 长江漫滩区软土渗透系数计算方法对比分析. 中国煤炭地质. 2024(02): 37-42 . 百度学术
3.	王宇虓，杜广印，刘松玉，杨泳，周同和，徐金涛. 振杆密实法加固粗粒混合土模型试验. 工程科学与技术. 2024(03): 99-108 . 百度学术
4.	樊书抗，杨正权，朱凯斌，赵艺颖，刘小生，赵剑明. 土的级配特征与连续级配方程研究. 水利学报. 2024(05): 597-606 . 百度学术
5.	郭海，张安银. 基于PCA的长江漫滩软弱黏性土渗透特性研究. 江苏建筑. 2024(04): 102-105 . 百度学术
6.	赵桂锋，蒋明杰，张振，王天成，梅国雄. 粗粒土缩尺级配的渗透系数规律试验. 工程科学与技术. 2024(05): 240-246 . 百度学术
7.	李诗琪，杨忠平，刘浩宇，高宇豪，刘新荣. 考虑间断级配影响的土石混合体水力侵蚀分异机理. 土木工程学报. 2024(10): 125-134 . 百度学术
8.	付宏渊，杨海涛，吴二鲁，曾铃，钟涛，姜懿芸. 考虑炭质泥岩颗粒破碎的级配演化预测模型. 水利学报. 2024(09): 1058-1070 . 百度学术
9.	杨锴，杨奇，徐方，徐俏东，韩学良. 考虑细粒含量的单参数连续级配方程研究. 铁道科学与工程学报. 2024(12): 5094-5103 . 百度学术
10.	曲诗章，刘晓明，黎莉，陈仁朋. 基于双分形级配模型参数的粗粒土渗透系数计算公式. 岩土工程学报. 2023(01): 144-152 . 本站查看
11.	侯龙清，袁晓铭，陈龙伟，李明东. 一种新型南55渗透仪研制及工程应用. 岩土工程学报. 2023(02): 419-425 . 本站查看
12.	李浩，李春艳，张嵩，谢英美. 建筑工程中地质特征及岩土工程支护研究. 能源与环保. 2023(01): 181-186 . 百度学术
13.	赵贵章，孔令莹，徐远志，王淑丽，王展. 银川平原典型介质的颗粒级配对渗透系数的影响研究. 中国农村水利水电. 2023(04): 203-207 . 百度学术
14.	张福海，徐嘉成，薛浩宇，刘峥嵘. 级配分布对杂填土地基互嵌沉降影响的试验分析. 河南科学. 2023(05): 730-737 . 百度学术
15.	林玉祥，林浩东，莫品强，褚锋，庄培芝. 基于XGBoost的堆场软土渗透系数反演研究. 西安理工大学学报. 2023(01): 133-140 . 百度学术
16.	袁仕方，曹志翔，韩志洋，张玲洁. 藏东南粗粒土降雨入渗影响因素试验分析. 高原农业. 2022(02): 189-196 . 百度学术
17.	丁林楠，李国英，魏匡民. 描述土体级配分布的级配方程及其适用性. 岩土力学. 2022(S1): 173-183 . 百度学术
18.	段钊，袁林，毕银丽，王凯，吴延斌，张庆. 紫花苜蓿根系-黄土复合体剪切特性与库仑修正模型. 煤田地质与勘探. 2022(12): 85-95 . 百度学术
19.	骆莉莎，周昕，林军. 颗粒形态对粗粒土渗透系数影响的数值模拟研究. 湖南工业职业技术学院学报. 2021(01): 93-96 . 百度学术