考虑注浆圈作用的体外排水隧道渗流场解析研究

李林毅; 阳军生; 高超; 夏万友; 麻彦娜

doi:10.11779/CJGE202001015

考虑注浆圈作用的体外排水隧道渗流场解析研究 English Version

1.
中南大学土木工程学院,湖南　长沙　410075
2.
大永高速公路投资开发有限公司,云南　昭通　657000
3.
湖南财政经济学院工程管理学院,湖南　长沙　410205

基金项目:

国家重点研发计划项目 2017YFB1302600

中南大学中央高校基本科研业务费专项资金项目 2019zzts291

详细信息

作者简介:
李林毅（1994— ）,男,湖南郴州人,博士研究生,从事隧道工程防排水体系研究工作。E-mail：tunnel_lly@csu.edu.cn

通讯作者:
阳军生, E-mail：jsyang@csu.edu.cn

中图分类号: TU45
计量
- 文章访问数: 343
- HTML全文浏览量: 13
- PDF下载量: 196
出版历程
- 收稿日期: 2019-04-09
- 网络出版日期: 2022-12-07
- 刊出日期: 2019-12-31

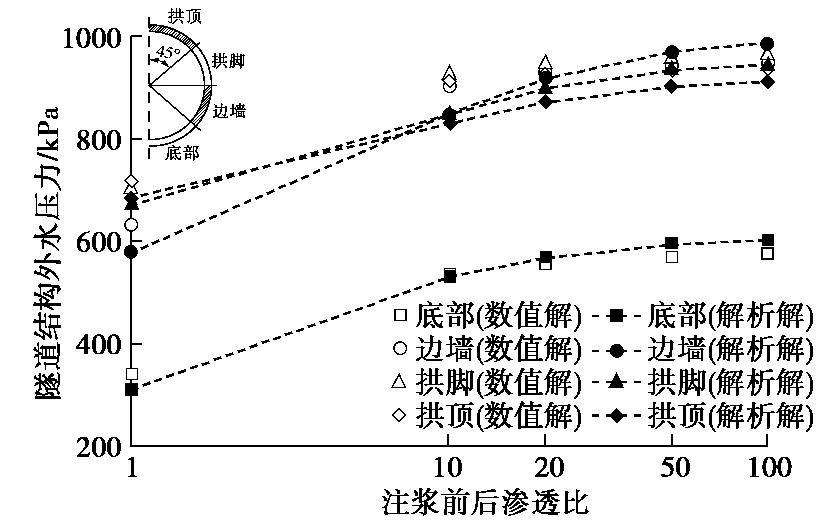
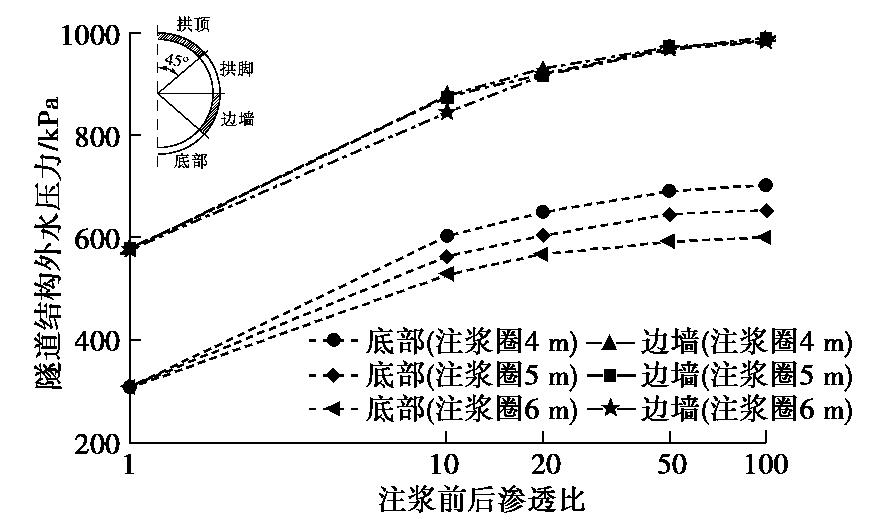
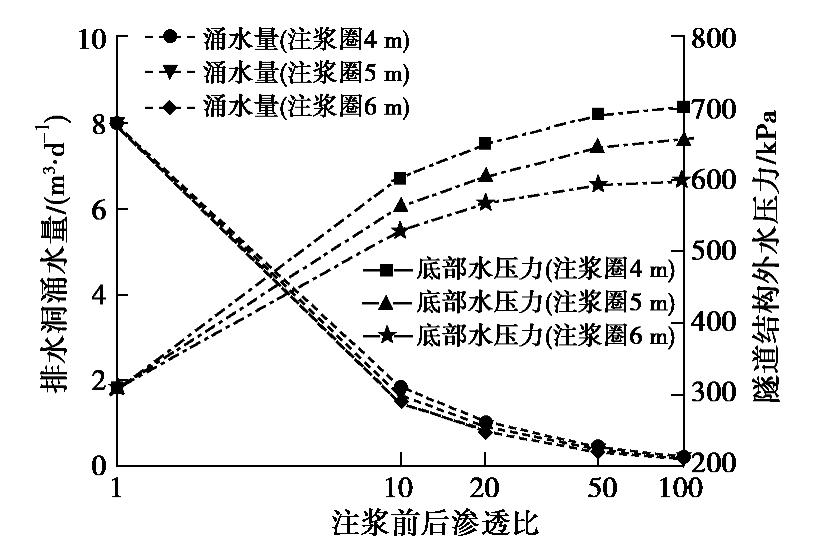
Analytical study on seepage field of tunnels with external drainage considering effect of grouting rings

1.
School of Civil Engineering, Central South University, Changsha 410075, China
2.
Dayong Highway Investment Development Co., Ltd., Zhaotong 657000, China
3.
School of Engineering Management, Hunan University of Finance and Economics, Changsha 410205, China

摘要

摘要: 体外排水方式在隧道工程中已得到逐步应用,但考虑注浆作用的体外排水隧道渗流场解析理论未见报道,导致理论滞后于工程实践。基于镜像法与渗流力学理论,提出了考虑注浆圈作用的体外排水隧道渗流场理论模型,通过解析退化、数值仿真两种方法共同验证了理论模型及解析公式的正确性,探讨了注浆圈渗透系数与厚度对涌水量、隧道外水压力的影响规律。分析结果表明：注浆圈渗透系数对体外排水隧道渗流场存在显著影响,随注浆渗透系数比值增大,涌水量可得到明显控制,但会引起外水压力的增长；注浆圈厚度影响相对较小,其影响主要在于厚度值越大时能一定程度上加强对底部结构外水压力的控制。提出了兼顾隧道限排要求与隧底水压力控制效果的合理注浆圈参数。研究成果以期为体外排水隧道注浆参数设计及施工实践提供参考。
- 体外排水方式 /
- 渗流力学 /
- 渗流场 /
- 涌水量 /
- 水压力 /
- 隧道 /
- 注浆圈参数
Abstract: The external drainage method has been gradually applied in the tunnel engineering, but the analytical theory of the seepage field of the external drainage tunnel considering the grouting effect has not been reported, which leads to that the theory lags behind engineering practice. Based on the mirror image method and the theory of seepage mechanics, the theoretical model of seepage field of the external drainage tunnel considering grouting rings is proposed. The correctness of the formula is verified through the analytical degradation and numerical simulation. The influences of the permeability coefficient and thickness of the grouting rings on the water inflow and the water pressure outside the tunnel are discussed. The analysis results show that the permeability coefficient of grouting rings has a significant influence on the seepage field of external drainage tunnel, and with the increase of the ratio, the water inflow can be controlled obviously, but it will cause the increase of external water pressure. The influences of grouting ring thickness are relatively small, which mainly lies in that the greater the grouting ring thickness, the stronger the control of the bottom external water pressure. The reasonable parameters of grouting rings are put forward considering the requirements of groundwater environmental protection and the control effect of water pressure. The research results may provide reference for the design of grouting parameters and the construction practice of external drainage tunnels.
- external drainage method /
- percolation mechanics /
- seepage field /
- water inflow /
- water pressure /
- tunnel /
- grouting ring parameter

HTML全文

0. 引言

合理开发和利用地下空间已成为解决城市人口激增、空间拥挤、交通阻塞及环境污染等问题的重要途径。在城市相对集中的沿江和滨海等饱和软黏土区域,地下空间开发所引起的长期沉降相当显著,通常为总沉降的30%〜90%^[1-3]。长期沉降不仅影响地下空间自身安全,如隧道衬砌开裂和渗漏水等,还会对周围环境和邻近建/构筑物等产生危害,如地下管线变形过大和地面建筑倾斜等。从长期沉降的发展机理来看^[3],地下空间开发对周围土体产生扰动后,所引起的超孔隙水压力消散及土体的流变特性是产生长期沉降的两个重要因素。因此,研究黏弹性地基中隧道施工等地下空间开发活动所引起的洞周超孔隙水压力消散问题具有重要的理论意义和工程应用价值。

针对洞周超孔隙水压力消散问题,国内外学者展开了较为广泛的研究。Carter等^[4-5]以Biot固结理论为框架,推导了弹性地基中洞周超孔隙水压力以及土体应力场和位移场的解析计算方法,洞周边界分为完全透水和完全不透水两种情况。在此基础上,Li等^[6-7]通过引入半渗透边界条件,将上述解答拓展至弹性半空间体内具有有限渗透性边界的洞周超孔隙水压力消散问题。基于Terzaghi-Rendulic二维固结理论,王志良等^[8]及申林方等^[9]推导了洞周不透水条件下饱和弹性地基中超孔隙水压力的解析解,分析了渗透系数、土体弹性模量以及隧洞埋深等参数对超孔隙水压力消散的影响。上述研究均将土体视为弹性介质,没有考虑其流变特性。为考虑土体流变特性对洞周超孔隙水压力消散的影响,詹美礼等^[10]以Terzaghi-Rendulic二维固结理论为基础,采用三元件Merchant模型描述土体的流变特性,推导了洞周超孔隙水压力的解析解,洞周边界为完全透水和完全不透水两种情况。童磊^[3]将三元件Merchant模型推广至四元件Burgers模型,建立了相应的解析解,研究了土体特性对超孔隙水压力消散的影响。针对泥炭质土层盾构施工引起的长期沉降问题,王志良等^[11]采用五元件模型来描述泥炭质土的流变特性,耦合Terzaghi-Rendulic二维固结理论,建立了完全不透水边界条件下洞周超孔隙水压力的解析解。综合考虑洞周土体流变和衬砌半渗透特性,李翔宇等^[12]建立了半透水边界条件下黏弹性地基中洞周超孔隙水压力的解析解,分析了不同衬砌透水程度对超孔隙水压力消散和分布的影响。刘干斌等^[13]基于Biot固结理论,运用推广的李氏比拟法,建立了半透水边界条件下黏弹性地基中深埋洞周的超孔隙水解答,研究了深埋条件下洞周超孔隙水压力以及土体应力和位移场的变化规律。上述研究虽考虑了土体流变特性对洞周超孔隙水压力消散特性的影响,但均采用经典流变模型（即整数阶流变模型）来描述土体的流变特性。然而,试验研究表明^[14-15],经典流变模型有时难以很好地描述材料的流变特性,特别是在初始流变阶段,通常需要较多的元件组合才能获得较好的模拟精度。

分数阶流变模型是经典流变模型的进一步拓展和延伸,采用分数阶导数代替整数阶导数来描述元件的本构关系。众多学者发现,分数阶流变模型可以采用相对较少的模型参数来更好地模拟材料的流变特性^[16-17]。自Gemant^[18]首次建立分数阶流变模型描述材料的流变特性以来,分数阶流变模型已逐渐成为岩土工程等领域的研究热点之一。Bagley等^[19]从能量耗散角度对分数阶流变模型的本构方程进行讨论和验证。Koller^[20]建立了多个分数阶流变模型,并对其流变特性进行了研究。赵永玲等^[21]和孙雅珍等^[22]采用分数阶流变模型分别研究了橡胶材料和沥青路面的流变特性。在岩土工程领域,Yin等^[17]、刘林超等^[23]、孙海忠等^[24]、Zhu等^[25]、何利军等^[26]、李锐铎等^[27]采用分数阶Kelvin模型、分数阶Merchant模型、分数阶Burger模型以及分数阶五元件模型等来拟合不同地区或不同类型软黏土的流变试验数据,得到很好的拟合结果,证明了分数阶流变模型描述软黏土流变特性的有效性和适用性。在此基础上,Wang等^[28]、解益等^[29]、刘忠玉等^[15,30]将分数阶流变模型应用到饱和软黏土一维流变固结分析中,研究了一维固结条件下分数阶黏弹性地基中孔隙水压力消散及土体变形发展规律。汪磊等^[31]、李林忠等^[32]、田乙等^[33]进一步建立了单面半透水、双面半透水以及连续排水边界条件下分数阶黏弹性地基的一维固结问题,分析了复杂边界条件对超孔隙水压力消散的影响。基于分数阶流变模型,Huang等^[34-35]研究了一维降水以及砂井固结条件下黏弹性地基中的超孔隙水压力消散问题,分析了分数阶流变模型参数对超孔隙水压力消散的影响。但是,目前尚未见分数阶流变模型应用于洞周超孔隙水压力消散问题的相关研究。

在以上学者的研究基础上,本文引入分数阶流变模型对黏弹性地基中洞周超孔隙水压力消散问题进行研究和探讨。首先,基于分数阶Merchant模型和Terzaghi-Rendulic二维固结理论,建立分数阶黏弹性地基中超孔隙水压力消散的控制方程；其次,借助保角变换、分离变量、Laplace变换及逆变换等方法,建立洞周超孔隙水压力的解答及其计算方法,并与文献已有解答进行对比；最后,探讨分数阶流变模型参数和边界条件对洞周超孔隙水压力消散特性的影响。

1. 解析问题的描述

1.1 分数阶Merchant模型

如图1所示,分数阶Merchant模型为三元件模型,由一个弹簧元件和一个Kelvin体所组成。基于分数阶微积分理论,分数阶流变模型采用分数阶导数关系来描述传统整数阶流变模型中的Abel黏壶。基于此,分数阶Merchant模型的总应力和总应变可以表示为^[25]

${\begin{array}{l} ε = ε_{1} + ε_{2}, \\ σ = E_{1} ε_{1} = E_{2} ε_{2} + E_{2} λ^{α}^{RL} D_{t}^{^{α}} ε_{2} 。 \end{array}$

(1)

图 1 分数阶Merchant模型

Figure 1. Fractional-derivative Merchant model

下载: 全尺寸图片幻灯片

式中 $σ$ 为总应力； $ε$ 为总应变； $ε_{1}$ 和 $ε_{2}$ 分别为弹簧元件和Kelvin体所产生的应变； $E_{1}$ 和 $E_{2}$ 为弹簧元件和Kelvin体的弹性模量； $λ = η / E_{2}$ 为Kelvin体的黏滞时间, $η$ 为其Abel黏壶的黏滞系数, $t$ 为时间, $^{RL} D_{t}^{^{α}}$ 为Riemann-Liouville型分数阶导数,其定义为^[16]

$^{RL} D_{t}^{α} ε (t) = \frac{1}{Γ (n - α)} \frac{d}{d t} \int_{0}^{t} {(t - τ)}^{n - α - 1} ε (τ) d τ$ ,

(2)

式中, $Γ (\cdot)$ 为Gamma函数, $α \in [n - 1, n)$ 为分数阶阶次, $n \geq 1$ 为自然数, $τ$ 为积分变量。对于分数阶流变模型,通常取 $0 \leq α \leq 1$ 。

对式（1）进行拉普拉斯变换,整理得到

$L (ε) = \frac{1}{E_{1}} (1 + \frac{κ}{λ^{α} s^{α} + 1}) L (σ)$ 。

(3)

式中, $κ = E_{1} / E_{2}$ , $L (\cdot)$ 表示拉普拉斯变换, $s$ 为一个复变量。

令 $σ = H (t)$ ,其中 $H (t)$ 为Heaviside函数,则利用卷积定理和拉普拉斯逆变换,由式（3）可以得到分数阶Merchant模型的柔度函数 $J (t)$ 为

$J (t) = \frac{1}{E_{1}} L^{- 1} (\frac{1}{s} + \frac{1}{s} \cdot \frac{κ}{λ^{α} s^{α} + 1})$ ,

(4)

式中, $L^{- 1} (\cdot)$ 表示拉普拉斯逆变换。当 $α = 1$ 时,式（4）可简化为

$J (t) = \frac{1}{E_{1}} [1 + κ (1 - e^{- \frac{t}{λ}})]$ 。

(5)

式（5）为整数阶Merchant模型的柔度函数^[9]。当 $α = 0$ 时,式（4）可简化为

$J (t) = \frac{κ + 2}{2 E_{1}}$ 。

(6)

式（6）为线弹性模型的柔度函数^[10]。可见,线弹性模型和整数阶Merchant模型均可视为分数阶Merchant模型的两个特例。

1.2 计算模型与控制方程

分析时,将洞周饱和软黏土层视为带圆孔的半无限平面,如图2所示。图2中,h为洞周埋深,r₀为洞周外径,C为平面坐标原点,D为无限远处的点,S区域为洞周饱和软黏土层。为了便于理论推导,本文采用如下假设^[10-12]：①饱和软黏土为各向同性介质,其应力应变关系服从分数阶Merchant模型,且所有黏弹性参数均为常数；②孔隙水和土颗粒的压缩可忽略不计,孔隙水流动服从达西定律,且饱和软黏土的渗透系数为常数；③土体变形十分微小,可忽略其对坐标的影响；④采用Terzaghi-Rendulic固结理论,土体中各点变形完全自由,且其所承受的总应力不随时间变化。基于上述假设,饱和软黏土二维固结状态下超孔隙水压力消散的偏微分方程可以表示为^[10-12]

$u_{x x} + u_{y y} = \frac{γ_{w}}{k m_{v}} (u_{t} + E_{1} \int_{0}^{t} u_{τ} J_{t - τ} d τ)$ 。

(7)

图 2 半无限空间中洞周土体计算模型图

Figure 2. Model for soft soil around tunnel in half space

下载: 全尺寸图片幻灯片

式中 $u$ 为超孔隙水压力； $u_{x x}$ 和 $u_{y y}$ 分别为 $u$ 关于x和y的二阶导数； $u_{t}$ 为 $u$ 关于t的一阶导数； $m_{v}$ 为土体压缩系数； $k$ 为渗透系数； $γ_{w}$ 为水的重度。

饱和软黏土所占区域为一个带圆孔的半无限平面,拥有地表和洞周内壁两个边界。在地表处,可以认为其完全透水,即超孔隙水压力为零；在洞周内壁处,通常按两种情况进行考虑：①施工期间,衬砌尚未完成,洞周内壁允许排水；②竣工后,洞周衬砌不允许排水。因此,两种情况下的边界条件（分别记为第一类边界、第二类边界条件）可以表示为

$\begin{matrix} {\begin{cases} {u |}_{y = 0} = 0 \\ {u |}_{x^{2} + {(y + h)}^{2} = r_{0}^{2}} = 0 \end{cases} & , & {\begin{cases} {u |}_{y = 0} = 0 \\ {u_{r} |}_{x^{2} + {(y + h)}^{2} = r_{0}^{2}} = 0 \end{cases} \end{matrix}$ 。

(8)

另外,在初始时刻 $t = 0$ 时,饱和软黏土层中的超孔隙水压力可表示为

${u |}_{t = 0} = u_{0} (x, y)$ 。

(9)

将式（4）代入式（7）中,并进行拉普拉斯变换,得到

$\frac{\partial^{2} \tilde{u}}{\partial x^{2}} + \frac{\partial^{2} \tilde{u}}{\partial y^{2}} = \frac{γ_{w}}{k m_{v}} (1 + \frac{κ}{λ^{α} s^{α} + 1}) (s \tilde{u} - u_{0})$ ,

(10)

式中, $\tilde{u} = L (u)$ 。式（10）为拉普拉斯域内基于分数阶Merchant模型的饱和软黏土中超孔隙水压力消散控制方程。在拉普拉斯域内,第一、二类边界条件式（8）可表示为

$\begin{matrix} {\begin{cases} {\tilde{u} |}_{y = 0} = 0 \\ {\tilde{u} |}_{x^{2} + {(y + h)}^{2} = r_{0}^{2}} = 0 \end{cases} & , & {\begin{cases} {\tilde{u} |}_{y = 0} = 0 \\ {{\tilde{u}}_{r} |}_{x^{2} + {(y + h)}^{2} = r_{0}^{2}} = 0 \end{cases} \end{matrix}$ 。

(11)

2. 超孔隙水压力解答推导与验证

2.1 保角变换

为研究图2中所示z平面内半无限空间中的单一孔洞问题,需采用保角变换,将其可转换为 $ζ$ 平面中的圆环域问题,如图3所示。映射函数为^[9-10]

$z = - i a \frac{1 + ζ}{1 - ζ}$ ,

(12)

图 3 保角变换映射计算模型图

Figure 3. Model after conformal mapping

下载: 全尺寸图片幻灯片

式中, $z = x + i y$ , $ζ = ξ + i η = ρ (\cos θ + i \sin θ)$ , $a = \sqrt{h^{2} - r_{0}^{2}}$ , $i = \sqrt{- 1}$ 为虚数单位。根据映射函数GOTOBUTTON ZEqnNum973390 \* MERGEFORMAT (12),图2中z平面上点C和D点分别映射成为图3中 $ζ$ 平面上点 $C^{'}$ 和 $D^{'}$ 点；洞周线 $| z + h i | = r_{0}$ 映射为圆环 $| ζ | = R$ ,水平线 $z = \bar{z}$ 映射为圆环 $| ζ | = 1$ ,求解域S区域映射为两个圆环间的 $\bar{S}$ 区域。

利用映射函数式（12）,方程（10）可以变换为

$\begin{matrix} \frac{\partial^{2} \tilde{u}}{\partial ρ^{2}} + \frac{1}{ρ} \frac{\partial \tilde{u}}{\partial ρ} + \frac{1}{ρ^{2}} \frac{\partial^{2} \tilde{u}}{\partial θ^{2}} = \frac{γ_{w}}{k m_{v}} \frac{4 a^{2}}{{(1 + ρ^{2} - 2 ρ \cos θ)}^{2}} \cdot \\ (1 + \frac{κ}{λ^{α} s^{α} + 1}) (s \tilde{u} - u_{0}) \end{matrix}$ 。

(13)

式中, $ρ$ 为径向坐标, $θ$ 为环向坐标。相应地,第一、二类边界条件式（11）变换为

$\begin{matrix} {\begin{cases} {\tilde{u} |}_{ρ = 1} = 0 \\ {\tilde{u} |}_{ρ = R} = 0 \end{cases} & , & {\begin{cases} {\tilde{u} |}_{ρ = 1} = 0 \\ {{\tilde{u}}_{ρ} |}_{ρ = R} = 0 \end{cases} \end{matrix}$ ,

(14)

式中, $R = (h - \sqrt{h^{2} - r_{0}^{2}}) / r_{0}$ 。

2.2 超孔隙水压力解答推导

方程（13）可采用分离变量法进行求解,令

$u (ρ, θ, t) = W (ρ, θ) T (t)$ ,

(15)

上述解答形式的拉普拉斯变换为

$\tilde{u} (ρ, θ, s) = W (ρ, θ) \tilde{T} (s)$ 。

(16)

将式（16）代入方程（13）中,得到如下两个方程：

$W_{, χ χ} + χ^{- 1} W_{, χ} + ϑ^{2} W = 0$ ,

(17)

$(1 + \frac{κ}{λ^{α} s^{α} + 1}) (s \tilde{T} - T_{0}) + \frac{k m_{v}}{4 a^{2} γ_{w}} ϑ^{2} \tilde{T} = 0$ 。

(18)

式中 $χ = {(1 + ρ^{2} - 2 ρ \cos θ)}^{- 1 / 2}$ ； $T_{0}$ 为时间项函数 $T (t)$ 的初始值,取 $T_{0} = 1$ ； $ϑ$ 为特征值。根据式（14）,方程（17）的第一、二类边界条件可表示为

$\begin{matrix} {\begin{cases} {W |}_{χ = χ_{1}} = 0 \\ {W |}_{χ = χ_{0}} = 0 \end{cases} & , & {\begin{cases} {W |}_{χ = χ_{1}} = 0 \\ {W_{χ} |}_{χ = χ_{0}} = 0 \end{cases} \end{matrix}$ ,

(19)

式中, $χ_{0} = {(1 + R^{2} - 2 R \cos θ)}^{- 1 / 2}$ , $χ_{1} = {(2 - 2 \cos θ)}^{- 1 / 2}$ 。

方程（17）为零阶Bessel方程,其通解为

$W (χ) = A J_{0} (ϑ χ) + B N_{0} (ϑ χ)$ ,

(20)

式中, $J_{0}$ 和 $N_{0}$ 分别为零阶Bessel函数和Neumann函数,A和B为待定系数。

将边界条件式（19）代入式（20）中,并确保式（20）为非零解,即系数A和B不同时为零,则可得到第一、二类边界条件下,关于 $ϑ$ 的特征方程分别为

$J_{0} (ϑ χ_{1}) N_{0} (ϑ χ_{0}) - N_{0} (ϑ χ_{1}) J_{0} (ϑ χ_{0}) = 0$ ,

(21)

$J_{0} (ϑ χ_{1}) N_{1} (ϑ χ_{0}) - N_{0} (ϑ χ_{1}) J_{1} (ϑ χ_{0}) = 0$ 。

(22)

式中, $J_{1}$ 和 $N_{1}$ 分别为一阶Bessel函数和Neumann函数。特征方程（21）和（22）中均含有变量 $ϑ$ 。对于每个确定的 $ϑ$ 值,均可从式（21）和（22）中分别求出n个特征值 $ϑ_{n}$ ,求解方法同文献[7]和[8]。第一类边界条件下的特征值 $ϑ_{n}$ 由式（21）求得,记为 $ϑ_{n 1}$ ；第二类边界条件下的特征值 $ϑ_{n}$ 由式（22）求得,记为 $ϑ_{n 2}$ 。对应于每个特征值 $ϑ_{n}$ ,方程（17）式的通解可表示为

$W_{n} (χ) = A_{n} J_{0} (ϑ_{n} χ) + B_{n} N_{0} (ϑ_{n} χ)$ ,

(23)

式中, $A_{n}$ 和 $B_{n}$ 为待定系数。由式（19）中 $χ = χ_{1}$ 处的边界,可得

$B_{n} = - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} A_{n}$ 。

(24)

将式（24）代入式（23）中,得到

$W_{n} (χ) = A_{n} [J_{0} (ϑ_{n} χ) - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} N_{0} (ϑ_{n} χ)]$ 。

(25)

另外,对于每个特征值 $ϑ_{n}$ ,式（18）可改写为

$(1 + \frac{κ}{λ^{α} s^{α} + 1}) (s {\tilde{T}}_{n} - T_{n, 0}) + β_{n} {\tilde{T}}_{n} = 0$ ,

(26)

式中, $β_{n} = k m_{v} ϑ_{n}^{2} / (4 a^{2} γ_{w})$ , $T_{n, 0}$ 为函数 $T_{n} (t)$ 的初始值,不失一般性,取 $T_{n, 0} = 1$ 。求解方程（26）,得到

${\tilde{T}}_{n} = \frac{λ^{α} s^{α} + κ + 1}{(λ^{α} s^{α} + κ + 1) s + (λ^{α} s^{α} + 1) β_{n}}$ 。

(27)

对式（27）两端做拉普拉斯逆变换,得到

$T_{n} = \frac{1}{2 πi} \int_{c - i \infty}^{c + i \infty} \frac{(λ^{α} s^{α} + κ + 1) e^{s t}}{(λ^{α} s^{α} + κ + 1) s + (λ^{α} s^{α} + 1) β_{n}} d s$ ,

(28)

式中, $c$ 为大于 ${\tilde{T}}_{n}$ 所有奇点实部的实数。通常,在 $0 < α < 1$ 的情况下,式（28）无解析表达式,其可采用Crump方法^[36]进行计算：

$T_{n} = \frac{e^{c t}}{T_{c}} [\frac{1}{2} {\tilde{T}}_{n} (c) + \sum_{l = 1}^{\infty} {\tilde{T}}_{n} (c + \frac{i l π}{T_{c}}) \cdot e^{\frac{i l π t}{T_{c}}}]$ ,

(29)

式中, $T_{c}$ 拉普拉斯逆变换的计算时间周期,通常可取为最大计算时间的两倍。

对应于n个特征值 $ϑ_{n}$ ,式（25）,（28）均可分别给出n个线性独立的解答 $W_{n}$ 和 $T_{n}$ 。将其进行线性叠加,并代入式（15）中,可得到超孔隙水压力的解答为

$\begin{matrix} u (ρ, θ, t) = \sum_{n}^{\infty} W_{n} (χ) T_{n} (t) \\ = \sum_{n}^{\infty} A_{n} [J_{0} (ϑ_{n} χ) - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} N_{0} (ϑ_{n} χ)] T_{n} (t) \end{matrix}$ 。

(30)

式中,系数 $A_{n}$ 由初始条件确定,即

$\sum_{n}^{\infty} W_{n} (χ) = u_{0}$ 。

(31)

将式（31）两端同时乘以 $W_{m}$ ,并将其沿 $χ$ 从 $χ_{0}$ 至 $χ_{1}$ 积分,则根据解答 $W_{n}$ 的正交性^[3,10],可得

$A_{n} = \frac{\int_{χ_{0}}^{χ_{1}} [J_{0} (ϑ_{n} χ) - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} N_{0} (ϑ_{n} χ)] u_{0} d χ}{\int_{χ_{0}}^{χ_{1}} {[J_{0} (ϑ_{n} χ) - \frac{J_{0} (ϑ_{n} χ_{1})}{N_{0} (ϑ_{n} χ_{1})} N_{0} (ϑ_{n} χ)]}^{2} d χ}$ 。

(32)

2.3 超孔隙水压力解答验证

为了验证分数阶黏弹性地基中洞周超孔隙水压力解答（30）的正确性,将其与已有的线弹性和黏弹性地基中的洞周超孔隙水压力解答进行对比。当 $α = 0$ 时,分数阶Merchant模型退化为线弹性模型。此时,式（28）可表示为

$T_{n} = \frac{1}{2 πi} \int_{c - i \infty}^{c + i \infty} \frac{(κ + 2) e^{s t}}{(κ + 2) s + 2 β_{n}} d s = e^{- {β^{'}}_{n} t}$ ,

(33)

式中, ${β^{'}}_{n} = 2 β_{n} / (κ + 2)$ 。对应的,超孔隙水压力解答（30）可表示为

$u = \sum_{n}^{\infty} W_{n} e^{- {β^{'}}_{n} t}$ 。

(34)

当 $α = 1$ 时,分数阶Merchant模型退化为整数阶Merchant模型。此时,式（28）可表示为

$\begin{array}{l} T_{n} = \frac{1}{2 πi} \int_{c - i \infty}^{c + i \infty} \frac{(λ s + κ + 1) e^{s t}}{(λ s + κ + 1) s + (λ s + 1) β_{n}} d s \\ = \frac{1}{ω_{n, 1} - ω_{n, 2}} \sum_{l = 1}^{2} {(- 1)}^{l + 1} (ω_{n, l} - \frac{1 + κ}{λ}) e^{- ω_{n, l} t} \end{array}$ 。

(35)

其中,

$\begin{matrix} ω_{n, 1} \\ ω_{n, 2} \end{matrix} = \frac{1}{2} [\frac{1 + κ + λ β_{n}}{λ} \pm \sqrt{{(\frac{1 + κ}{λ} + β_{n})}^{2} - \frac{4 β_{n}}{λ}}]$ 。

(36)

对应超孔隙水压力解答（30）可表示为

$u = \sum_{n}^{\infty} \sum_{l = 1}^{2} \frac{{(- 1)}^{l + 1} W_{n}}{ω_{n, 1} - ω_{n, 2}} (ω_{n, l} - \frac{1 + κ}{λ}) e^{- ω_{n, l} t}$ 。

(37)

解答（34）与申林方等^[9]所建立的线弹性地基中洞周超孔隙水压力解答一致；解答（37）与詹美礼等^[10]所建立的整数阶Merchant黏弹性地基中洞周超孔隙水压力解答一致。可见,本文解答是正确的,且线弹性和整数阶Merchant黏弹性地基中洞周超孔隙水压力解答为本文解答的两个特例。

3. 超孔隙水压力消散特性分析

为分析分数阶黏弹性地基中洞周超孔隙水压力的消散特性,选取某隧道工程参数为^[10]：半径 $r_{_{0}} = 5 m$ ,埋深 $h = 15 m$ ,地面堆载 $q = 200 kPa$ ,饱和软黏土的渗透系数 $k = 1.99 mm/d$ ,弹性模量 $E_{1} = 6 MPa$ ,泊松比 $μ = 0.3$ ,黏滞系数 $η = 4.92 \times 10^{5} MPa \cdot d$ 。为简化分析,假设地面堆载为大面积均布堆载,其在洞周饱和软黏土中所引起的初始超孔隙水压力近似于均匀分布且等于堆载集度q,即 $u_{0} = q$ 。根据上述参数,利用式（30）即可计算获得分数阶黏弹性地基中洞周的超孔隙水压力值。

3.1 不同分数阶阶次下超孔隙水压力消散特性

分数阶阶次 $α$ 为分数阶Merchant模型描述饱和软黏土变形特性的一个量纲为“1”参数。当其在0和1之间变化时,Abel黏壶（也称为分数阶元件）的受力特性将介于理想固体和理想流体之间。分数阶阶次 $α$ 较小时,其受力特性与理想固体（即弹簧单元）相似,力的大小受变形和刚度控制；而分数阶阶次 $α$ 较大时,其受力特性与理想流体（即黏壶单元）相似,力的大小由变形率和黏滞系数控制。图4给出了不同分数阶阶次下洞周饱和软黏土中 $θ = 0$ 和 $θ = π / 2$ 处超孔隙水压力的消散规律。限于篇幅,这里只给出洞周内壁允许排水（即第一类边界）条件下的计算结果,洞周内壁不允许排水（即第二类边界）条件下的计算结果与之类似,不再列出。从图4可以看出,随着消散时间的增大,洞周超孔隙水压力消散曲线出现相互交叉的现象,即在不同的消散阶段,分数阶阶次 $α$ 对超孔隙水压力消散特性的影响是不同的。在消散初期,分数阶阶次 $α$ 越大,超孔隙水压力消散越快,即在同一时刻,超孔隙水压力越小；而在消散后期,分数阶阶次 $α$ 越大,超孔隙水压力则消散越慢,即在同一时刻,超孔隙水压力越大。上述现象是由分数阶元件的力学特性所引起的。在消散初期,饱和软黏土层的变形尚未得到充分发展,变形很小,其对土层有效应力的影响很小。此时,土体有效应力主要由变形率所主导。分数阶阶次 $α$ 越大,分数阶元件的受力特性越接近理想流体,其力的大小受到变形率的影响越大,从而使得在相同变形率的条件下,所引起的土体有效应力越大,即土体中的超孔隙水压力消散越快。而在消散后期,饱和软黏土层的变形得到了充分的发展,其对土体有效应力起到了主导作用。在此阶段,分数阶阶次 $α$ 越小,则分数阶元件的受力特性则越接近理想固体,其力的大小受变形的影响则更为明显,从而使得相同变形的条件下,所引起的土体有效应力越大,即土体中的超孔隙水压力消散越快；反之,分数阶阶次 $α$ 越大,土体中的超孔隙水压力消散则越慢。

图 4 不同分数阶阶次下超孔隙水压力的消散规律

Figure 4. Dissipation of excess pore-water pressure under different fractional orders

下载: 全尺寸图片幻灯片

3.2 不同模量比下超孔隙水压力消散特性

模量比 $κ$ 为分数阶Merchant模型中独立弹簧单元的弹性模量 $E_{1}$ 与Kelvin体中弹簧单元的弹性模量 $E_{2}$ 之比。计算时, $E_{1}$ 取为6 MPa, $E_{2} = E_{1} / κ$ 随着模量比 $κ$ 发生变化。针对洞周内壁允许排水的情况,图5给出了不同模量比下洞周饱和软黏土中 $θ = 0$ 和 $θ = π / 2$ 处超孔隙水压力的消散规律。可以看出,随着模量比的增大,洞周超孔隙水压力消散越慢,即在同一时刻,超孔隙水压力越大。这是因为,在给定 $E_{1}$ 的情况下,模量比 $κ$ 越大,所对应的 $E_{2}$ 则越小,即土层越软。在超孔隙水压力消散即土体变形过程中,土层越软,土中有效应力发展得越慢,从而使得超孔隙水压力消散得越慢。在超孔隙水压力消散前期即土体变形相对较小时,模量比 $κ$ 所产生的影响较小；而在超孔隙水压力消散中后期即土体变形得到较为充分的发展时,模量比 $κ$ 所产生的影响则变得较为明显。

图 5 不同模量比下超孔隙水压力的消散规律

Figure 5. Dissipation of excess pore-water pressure under different modulus ratios

下载: 全尺寸图片幻灯片

3.3 不同黏滞系数下超孔隙水压力消散特性

黏滞系数是表征饱和软黏土流变特性的重要指标之一。土体的黏滞系数越大,土体的流变特性越显著,其沉降发展越缓慢,沉降完成所需的时间也越长^[37]。针对洞周内壁允许排水的情况,图6给出了不同黏滞系数下洞周饱和软黏土中 $θ = 0$ 和 $θ = π / 2$ 处超孔隙水压力的消散规律。可以看出,不同黏滞系数下,洞周超孔隙水压力的消散曲线出现相互交叉的现象,其与不同分数阶阶次下超孔隙水压力的消散现象类似,如图4所示。在消散前期,黏滞系数越大,超孔隙水压力消散得越快,即同一时刻,超孔隙水压力值越小；而在消散后期,黏滞系数越大,超孔隙水压力消散得越慢,即同一时刻,超孔隙水压力值越大。这种现象与黏弹性饱和软黏土一维固结中的超孔隙水压力消散现象相同^[38],其可采用分数阶Merchant模型的力学特性来解释。如图1所示,分数阶Merchant流变模型由一个独立弹簧和一个Kelvin体串联组成,二者承受的应力值相等,均为饱和软黏土所承受的有效应力。在消散前期,特别是初始阶段,饱和软黏土层所产生变形还非常小,其对土体有效应力的贡献和影响都很小。在这一阶段,土体有效应力主要由Kelvin体中Abel黏壶承担。因此,较大的黏滞系数会诱发较大的土体有效应力,从而加速了超孔隙水压力的消散。在消散后期,饱和软黏土中的变形已得到了较为充分的发展,其对土体有效应力的贡献和影响变得更为明显,甚至起主导作用。土体的黏滞系数越大,其沉降发展就越缓慢,即同一时刻,沉降值越小。因此,在该阶段,黏滞系数越大,其沉降和有效应力发展越缓慢,从而使得超孔隙水压力消散得越慢。

图 6 不同黏滞系数下超孔隙水压力的消散规律

Figure 6. Dissipation of excess pore-water pressure under different viscosity coefficients

下载: 全尺寸图片幻灯片

3.4 不同边界条件下超孔隙水压力分布和消散特性

针对施工期间衬砌未完成和竣工后衬砌已完成的两种情况,本文建立了洞周允许排水和不允许排水两种边界条件下的超孔隙水压力解答。针对上述两种边界条件,图7给出了洞周饱和软黏土中 $θ = 0$ 和 $θ = π / 2$ 处在不同时刻的超孔隙水压力分布规律。可以看出,洞周允许排水时,超孔隙水压力在径向坐标 $ρ$ 的两端为零,其沿径向坐标 $ρ$ 呈现先增加而后减小的分布规律；洞周不允许排水时,超孔隙水压力在靠近洞周一侧为最大值,在远离洞周一侧为零,其沿径向坐标 $ρ$ 呈现逐渐减小的分布规律。在超孔隙水压力消散初期,边界条件所产生的影响主要体现在靠近洞周一侧；之后,其影响逐渐向远离洞周一侧延伸。此外,图7（a）和（b）的对比表明,与洞侧壁 $θ = 0$ 处超孔隙水压力的消散相比,洞顶 $θ = π / 2$ 处超孔隙水压力的消散更快,且超孔隙水压力消散前期,边界条件在洞顶 $θ = π / 2$ 处所产生的影响也更为明显。

图 7 不同边界条件下超孔隙水压力分布和消散规律

Figure 7. Distribution and dissipation of excess pore-water pressure under different boundary conditions

下载: 全尺寸图片幻灯片

4. 结论

本文基于分数阶导数理论,借助保角变换、拉普拉斯变换及逆变换方法,推导了分数阶Merchant模型的柔度函数,建立了分数阶黏弹性地基中洞周超孔隙水压力的解答及其计算方法,分析了分数阶阶次、模量比、黏滞系数以及边界条件对超孔隙水压力消散特性的影响,取得以下4点结论。

（1）分数阶阶次和黏滞系数对超孔隙水压力消散特性的影响均呈现两个不同的阶段：消散初期,分数阶阶次和黏滞系数越大,超孔隙水压力消散越快；消散后期,分数阶阶次和黏滞系数越大,超孔隙水压力则消散越慢。

（2）模量比越大即饱和软黏土层越软,超孔隙水压力消散越慢,且模量比的影响在超孔隙水压力消散中后期更为明显。

（3）洞周允许排水时,超孔隙水压力沿径向呈先增加后减小的分布规律；洞周不允许排水时,其沿径向呈逐渐减小的分布规律。消散初期,边界条件对超孔隙水压力消散的影响主要体现在靠近洞周一侧,之后,其影响逐渐向远离洞周一侧延伸。

（4）将本文解答退化为线弹性和整数阶黏弹性地基的情况,并与已有解答进行对比,验证了本文解答的可靠性。同时,本文解答将洞周超孔隙水压力消散问题延伸至分数阶导数层次,更具一般性,可为相应的工程实例分析提供理论支撑。

图 1 体外排水方式及其渗流路径

Figure 1. External drainage method and its seepage path

下载: 全尺寸图片幻灯片

图 2 渗流解析模型及参数设定

Figure 2. Analytical seepage model and setting of parameters

下载: 全尺寸图片幻灯片

图 3 渗流计算模型分区

Figure 3. Zoning of seepage model

下载: 全尺寸图片幻灯片

图 4 各区模型计算参数

Figure 4. Parameters for various zone models

下载: 全尺寸图片幻灯片

图 5 镜像法示意图

Figure 5. Sketch of mirror image method

下载: 全尺寸图片幻灯片

图 6 数值模型基本尺寸及边界条件

Figure 6. Dimensions and boundary conditions of numerical models

下载: 全尺寸图片幻灯片

图 7 隧道涌水量验证情况

Figure 7. Verification of tunnel water inflow

下载: 全尺寸图片幻灯片

图 8 注浆圈4 m时隧道结构外水压力情况

Figure 8. Water pressures outside tunnel (grouting ring of 4 m)

下载: 全尺寸图片幻灯片

图 9 注浆圈5 m时隧道结构外水压力情况

Figure 9. Water pressures outside tunnel (grouting ring of 5 m)

下载: 全尺寸图片幻灯片

图 10 注浆圈6 m时隧道结构外水压力情况

Figure 10. Water pressures outside tunnel (grouting ring of 6 m)

下载: 全尺寸图片幻灯片

图 11 各工况下典型位置外水压力变化情况

Figure 11. Variation of water pressure in typical location of tunnel

下载: 全尺寸图片幻灯片

图 12 各工况下隧道渗流特征参数情况汇总

Figure 12. Summary of seepage characteristic parameters under different conditions

下载: 全尺寸图片幻灯片

表 1 分析计算工况

Table 1 Analytical and computational working conditions

工况编号	注浆圈厚度/m	注浆圈渗透系数/(m·s^-1)	注浆前后渗透系数比
1（未注浆）	0	1×10^-6	1
2—1	4	1×10^-7	10
2—2		5×10^-8	20
2—3		2×10^-8	50
2—4		1×10^-8	100
3—1	5	1×10^-7	10
3—2		5×10^-8	20
3—3		2×10^-8	50
3—4		1×10^-8	100
4—1	6	1×10^-7	10
4—2		5×10^-8	20
4—3		2×10^-8	50
4—4		1×10^-8	100

下载: 导出CSV

参考文献(21)

[1]	代鸿明. 运营铁路隧道水害引发的仰拱起鼓及衬砌开裂防治技术研究[J]. 现代隧道技术, 2016, 53(3): 202-206. DAI Hong-ming. Prevention and treatment of invert heaving and lining cracking induced by water disasters in operating railway tunnels[J]. Modern Tunnelling Technology, 2016, 53(3): 202-206. (in Chinese)
[2]	郑波, 吴剑, 吴晓龙. 水压力作用下隧道底部结构裂损机理及其防治[J]. 铁道工程学报, 2017, 34(1): 91-96. doi: 10.3969/j.issn.1006-2106.2017.01.017 ZHENG Bo, WU Jian, WU Xiao-long. Research on the cracking mechanism and treatment measures of tunnel invert filling structure under the action of water pressure[J]. Journal of Railway Engineering Society, 2017, 34(1): 91-96. (in Chinese) doi: 10.3969/j.issn.1006-2106.2017.01.017
[3]	杜明庆, 张顶立, 张素磊, 等. 高速铁路隧道仰拱结构受力现场实测分析[J]. 中国铁道科学, 2017(5): 53-61. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201705010.htm DU Ming-qing, ZHANG Ding-li, ZHANG Su-lei, et al. Field test and analysis of mechanical characteristics of tunnel invert structure for high-speed railway[J]. China Railway Science, 2017(5): 53-61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201705010.htm
[4]	肖广智, 薛斌. 向莆铁路隧道道床积水、轨道隆起病害整治技术[J]. 现代隧道技术, 2015, 52(3): 200-204. XIAO Guang-zhi, XUE Bin. Treatment of bed waterlogging and track heaving in tunnels on the Xiangtang-Putian Railway[J]. Modern Tunnelling Technology, 2015, 52(3): 200-204. (in Chinese)
[5]	李林毅, 阳军生, 麻彦娜, 等. 体外排水方式在隧道工程中的研究与应用[J]. 铁道学报.(已录用). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB202010017.htm LI Lin-yi, YANG Jun-sheng, MA Yan-na, et al. Research and application of extracorporeal drainage method in tunnel project[J]. Journal of the China Railway Society. (accepted) (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB202010017.htm
[6]	李林毅, 阳军生, 张峥, 等. 深埋式中心水沟排水隧道渗流场解析研究[J]. 浙江大学学报(工学版), 2018, 52(11): 2050-2057. doi: 10.3785/j.issn.1008-973X.2018.11.002 LI Lin-yi, YANG Jun-sheng, ZHANG Zheng, et al. Analytical study of seepage field of deep-buried central ditch drainage tunnel[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(11): 2050-2057. (in Chinese) doi: 10.3785/j.issn.1008-973X.2018.11.002
[7]	NAM S W, BOBET A. Liner stresses in deep tunnels below the water table[J]. Tunnelling and Underground Space Technology, 2006, 21(6): 626-635. doi: 10.1016/j.tust.2005.11.004
[8]	ARJNOI P, JEONG J H, KIM C Y, et al. Effect of drainage conditions on porewater pressure distributions and lining stresses in drained tunnels[J]. Tunnelling and Underground Space Technology, 2009, 24(4): 376-389. doi: 10.1016/j.tust.2008.10.006
[9]	樊祥喜, 阳军生, 麻彦娜, 等. 不同防排水方式下富水隧道受列车振动荷载动力影响分析[J]. 铁道科学与工程学报, 2018, 15(11): 2901-2908. FAN Xiang-xi, YANG Jun-sheng, MA Yan-na, et al. Analysis of dynamic influence of train vibration load on water rich tunnel under different water proof and drainage ways[J]. Journal of Railway Science and Engineering, 2018, 15(11): 2901-2908. (in Chinese)
[10]	李洪涛. 排水模式对高速铁路隧道仰拱变形影响研究[D]. 成都: 西南交通大学, 2018. LI Hong-tao. Study on the Influence of Drainage Mode on the Deformation of Inverted Arch of High Speed Railway Tunnels[D]. Chengdu: Southwest Jiaotong University, 2018. (in Chinese)
[11]	LI P F, LIU H L, ZHAO Y, et al. A bottom-to-up drainage and water pressure reduction system for railway tunnels[J]. Tunnelling and Underground Space Technology, 2018, 81: 296-305.
[12]	姚希磊. 隧道深埋式中心水沟施工技术研究[J]. 铁道建筑技术, 2017(6): 97-99. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJS201706023.htm YAO Xi-lei. Research on the construction technology for deep-buried ditch in tunnel[J]. Railway Construction Technology, 2017(6): 97-99. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJS201706023.htm
[13]	赵乐. 基于堵水限排高压富水区山岭隧道防排水技术研究[D]. 成都: 西南交通大学, 2017. ZHAO Le. Study on Waterproof and Drainage Technology of Mountain Tunnel in High Pressure and Rich Water Area Based on Blocking Groundwater and Limiting Discharge[D]. Chengdu: Southwest Jiaotong University, 2017. (in Chinese)
[14]	黄锋, 魏源泉, 蒋树屏, 等. 高压富水区限排隧道围岩与衬砌水压力场研究[J]. 地下空间与工程学报, 2017, 13(1): 146-152. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201701021.htm HUANG Feng, WEI Yuan-quan, JIANG Shu-ping, et al. Water pressure field study of surrounding rock and lining of controlling emission tunnel in high-pressure and water-rich zone[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(1): 146-152. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201701021.htm
[15]	马青, 罗禄森, 阳军生, 等. 岩溶富水区深埋水沟排水隧道注浆圈参数研究[J]. 隧道建设, 2018, 38(11): 1793-1799. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201811009.htm MA Qing, LUO Lu-sen, YANG Jun-sheng, et al. Study of parameters of grouting circle for deep-ditch drainage tunnel in water-rich karst area[J]. Tunnel Construction, 2018, 38(11): 1793-1799. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201811009.htm
[16]	邹育麟, 何川, 胡雄玉, 等. 富水区隧道合理防排水型式及注浆加固参数研究[J]. 防灾减灾工程学报, 2014, 34(4): 485-491. ZOU Yu-lin, HE Chuan, HU Xiong-yu, et al. Study on reasonable waterproof and drainage pattern and grouting parameter of rich water tunnel[J]. Journal of Disaster Prevention and Mitigation Engineering, 2014, 34(4): 485-491. (in Chinese)
[17]	应宏伟, 朱成伟, 龚晓南. 考虑注浆圈作用水下隧道渗流场解析解[J]. 浙江大学学报(工学版), 2016, 50(6): 1018-1023. YING Hong-wei, ZHU Cheng-wei, GONG Xiao-nan. Analytic solution on seepage field of underwater tunnel considering grouting circle[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(6): 1018-1023. (in Chinese)
[18]	翟云芳. 渗流力学[M]. 北京: 北京石油工业出版社, 2009: 25-27. ZHAI Yun-fang. Seepage Mechanics[M]. Beijing: Petroleum Industry Press, 2009: 25-27. (in Chinese)
[19]	Itasca . FLAC^3D version 5.0 User's Manual[M]. Minnesota: Mineapolis ICG, 2012.
[20]	王一鸣. 高水压岩溶隧道衬砌结构受力特征和防排水设计研究[D]. 长沙: 中南大学, 2014. WANG Yi-ming. Research on Mechanical Characters and Drainage of Karst Tunnel with High Water Pressure[D]. Changsha: Central South University, 2014. (in Chinese)
[21]	程盼. 基于生态平衡的隧道地下水渗控方法及限排水标准研究[D]. 长沙: 中南大学, 2014. CHENG Pan. Groundwater Seepage and Control Method for Tunnel and Limit Drainage Criterion Based on Ecological Balance[D]. Changsha: Central South University, 2014. (in Chinese)

施引文献(13)

期刊类型引用(8)

1.	龚昭祺，林廷松，李文乾，胡安峰. 考虑渗透各向异性的隧道周围饱和软土固结特性分析. 地基处理. 2024(01): 16-22 . 百度学术
2.	谢森林，胡安峰，肖志荣，汪美慧，胡训健，陈俞超. 基于广义Voigt模型的半渗透边界隧道周围饱和软土固结分析. 岩土力学. 2024(07): 2024-2036 . 百度学术
3.	谢森林，胡安峰，肖志荣，陈缘，汪美慧. 渗漏病害加剧影响下隧道周围土体流变固结分析. 岩石力学与工程学报. 2024(10): 2570-2580 . 百度学术
4.	仉文岗，唐学成，刘汉龙，杨文钰，刘智成，王鲁琦，李红蕊. 静-动荷载作用下欠固结软土盾构隧道长期沉降与最优埋深计算方法. 隧道建设(中英文). 2024(09): 1829-1840 . 百度学术
5.	丁峰，程扬，钱春宇，宋春雨，陈龙珠. 双洞隧道地铁运行引起的软土地基振动及孔压研究. 土木工程与管理学报. 2024(05): 71-77 . 百度学术
6.	胡安峰，姜浩，肖志荣，谢森林，龚昭祺，李文乾. 基于分数阶模型的隧道周围土体非线性流变固结分析. 浙江大学学报(工学版). 2023(11): 2227-2234 . 百度学术
7.	张思峰，任子夤，郑帅，张驰. 黄河冲积平原区静压管桩超静孔隙水压力时空效应试验研究. 路基工程. 2022(01): 53-57 . 百度学术
8.	杨光，顾昊，刘尚蔚，包腾飞，孙锦，栾博文. 基于分数阶模式的高拱坝变形安全监控研究构想. 水利水电科技进展. 2022(05): 85-93+120 . 百度学术