马蹄形隧道拱脚裂纹对围岩稳定性的影响

周磊; 朱哲明; 刘邦; 邱豪; 董玉清

doi:10.11779/CJGE202001010

马蹄形隧道拱脚裂纹对围岩稳定性的影响 English Version

四川大学建筑与环境学院深地科学与工程教育部重点实验室,四川　成都610065

基金项目:

国家自然科学基金项目 11672194

四川省安全监管局安全生产科技项目 aj20170515161307

四川省科技计划项目 2018JZ0036

详细信息

作者简介:
周磊（1990— ）,男,博士,助理研究员,主要从事岩石断裂力学的研究工作。E-mail：zhouleittkx@126.com

通讯作者:
朱哲明, E-mail：zhemingzhu@hotmail.com

中图分类号: TU45;U45
计量
- 文章访问数: 0227
- HTML全文浏览量: 0
- PDF下载量: 0217
出版历程
- 收稿日期: 2019-04-03
- 网络出版日期: 2022-12-07
- 刊出日期: 2019-12-31

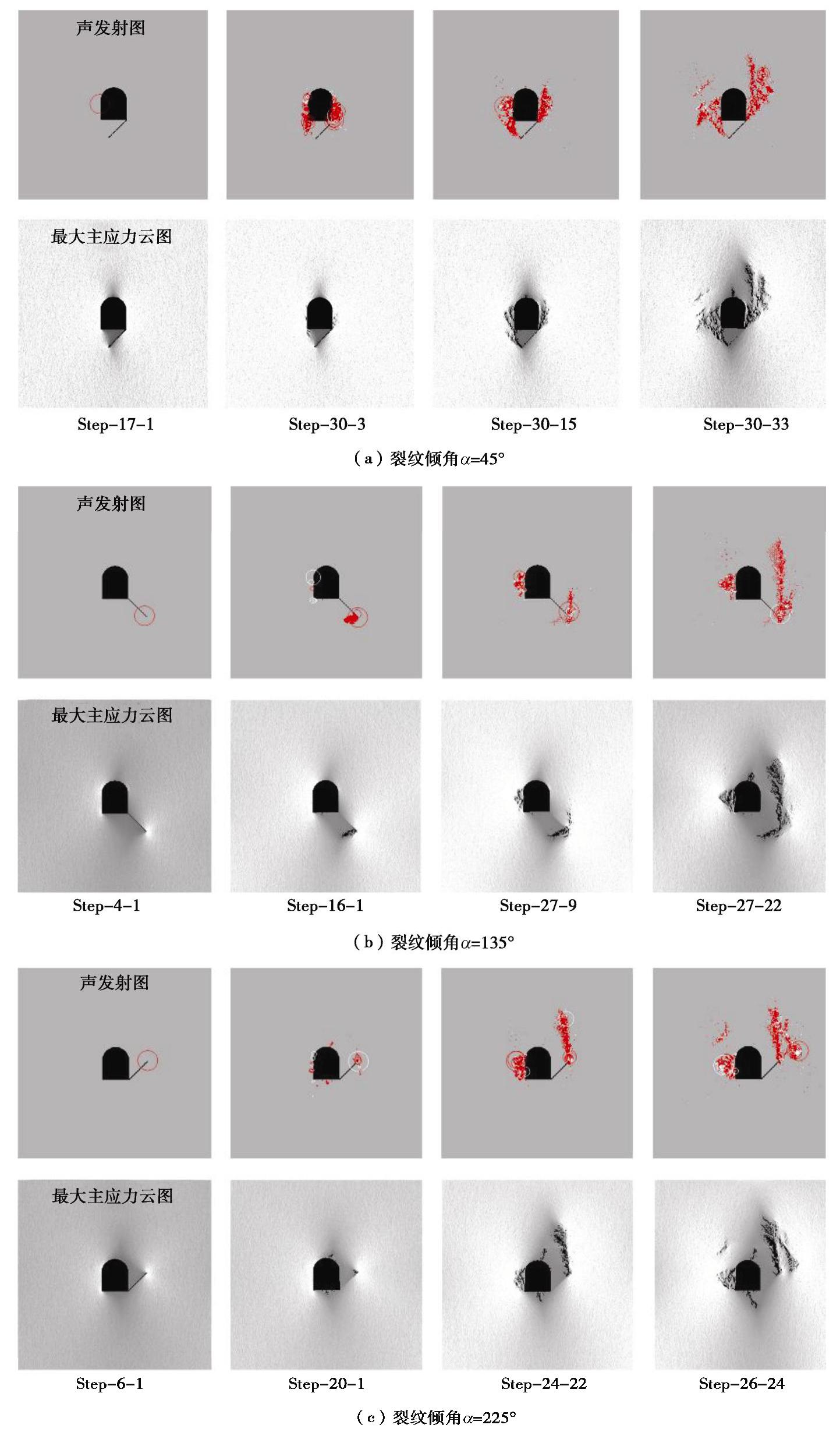
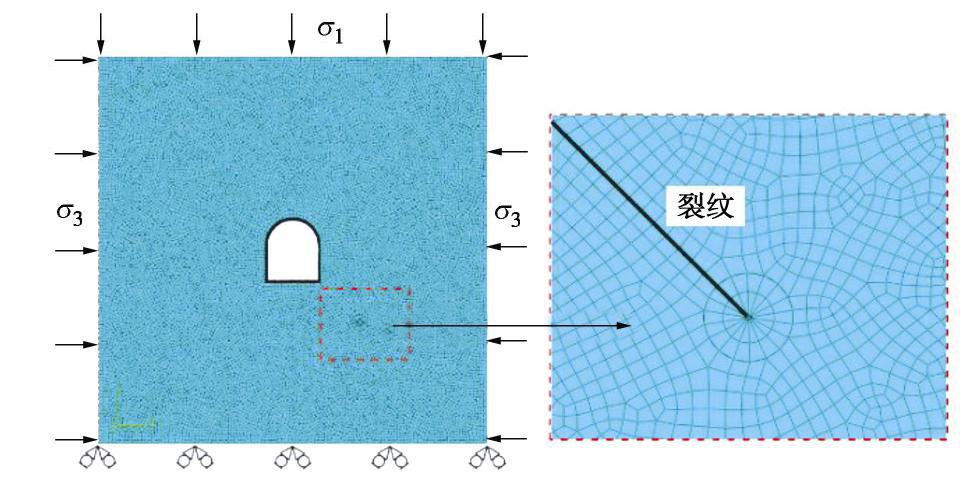
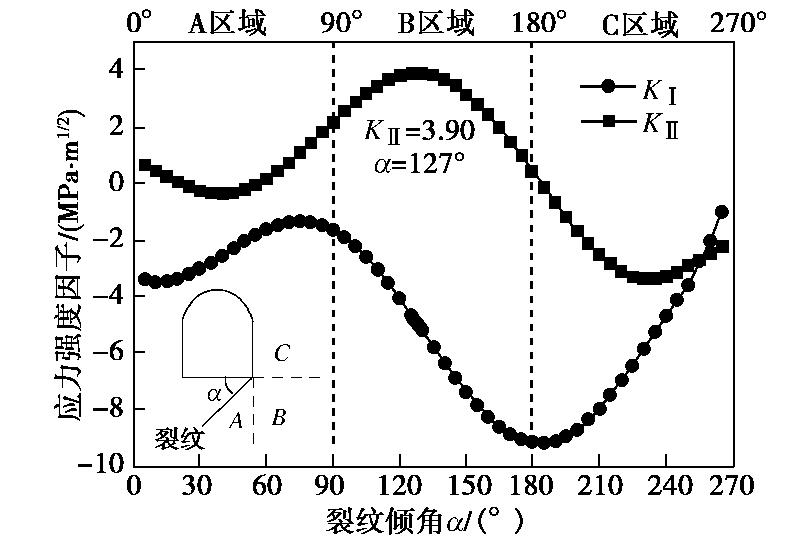
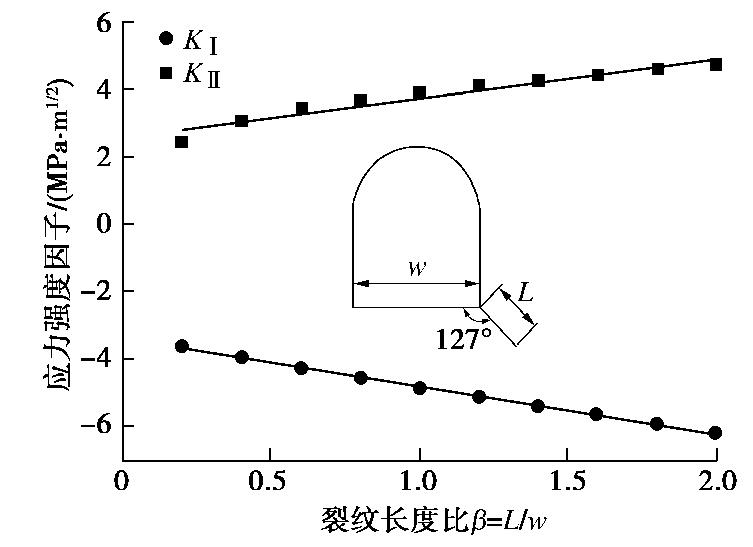
Influence of arch foot crack on stability of surrounding rock mass in horseshoe-shaped tunnels

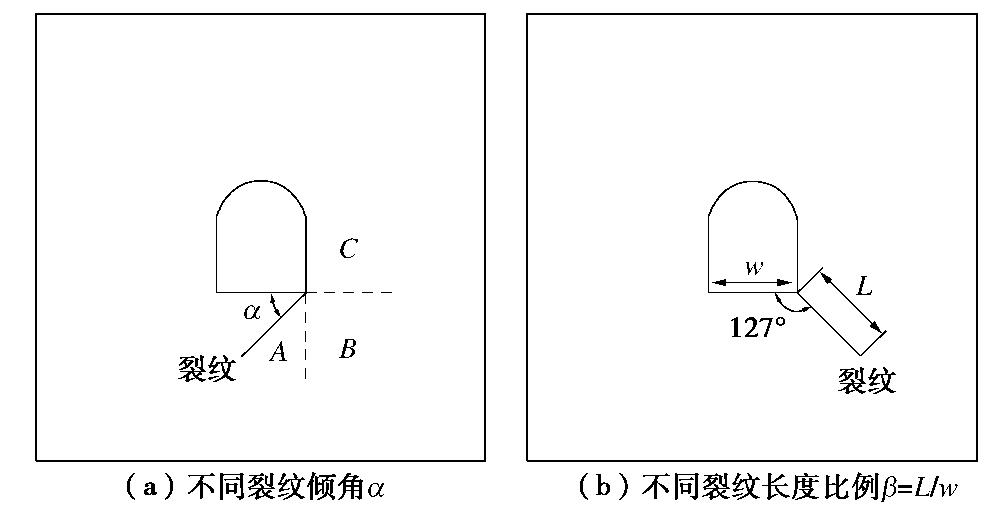
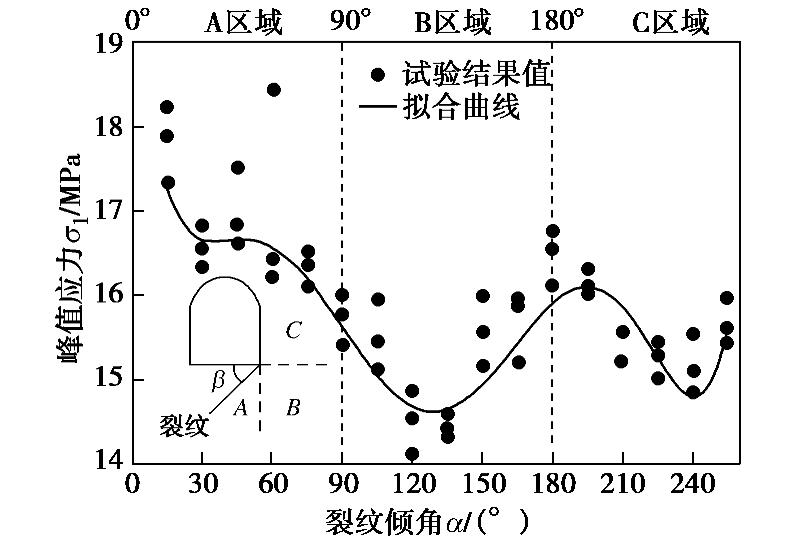
MOE Key Laboratory of Deep Underground Science and Engineering, College of Architecture and Environment, Sichuan University, Chengdu 610065, China

摘要

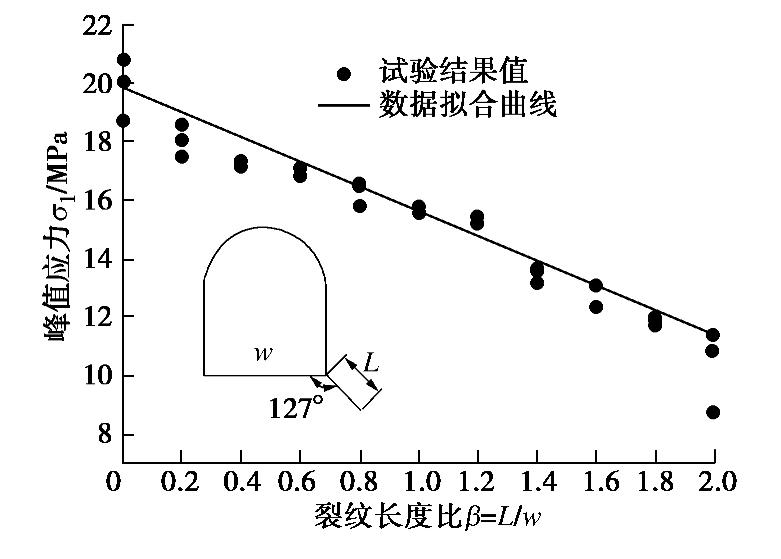
摘要: 详细研究了隧道拱脚处裂纹对围岩稳定性及破坏模式的影响,裂纹分两组进行设置：一是裂纹以拱脚交界点为圆心逆时针方向分布在A(0°< $α$ $α$ ≤90°),B(90°< $α$ $α$ ≤180°)及C(180°< $α$ $α$ ≤270°)区域,且与隧道底板面成夹角 $α$ $α$ ；二是裂纹倾角 $α$ $α$ 为127°,与隧道跨度成不同裂纹长度比β。采用物理模型试验和数值模拟对比分析拱脚裂纹的不利因素,随后选择砂岩材料制作隧道模型试件进行室内试验,得到裂纹因素对围岩强度的影响。数值模拟采用有限元程序分别计算裂纹尖端的应力强度因子与围岩损伤演化云图。通过两者对比论证可以得到如下结论：①裂纹在隧道拱脚位置处成不同倾角 $α$ $α$ 时,裂纹分布区域的危害程度可依次排列为B>C>A；②裂纹倾角 $α$ $α$ 在120°～135°时,裂纹对隧道整体的稳定性影响最大；③在双轴压缩载荷作用下,围岩的破坏行为主要是裂纹尖端与边墙的拉剪破坏及局部的拉伸破坏；④裂纹长度比β对围岩整体稳定性影响表征为线性反比例函数关系。
- 隧道 /
- 裂纹倾角 /
- 数值模拟 /
- 拱脚裂纹 /
- 围岩
Abstract: In order to clearly investigate the effect of a crack at the tunnel arch foot on the stability and failure patterns of horseshoe-shaped tunnels, the cracks are classified into two categories: one is that the cracks are distributed counterclockwise in the areas of A(0°< $α$ $α$ ≤90°), B(90°< $α$ $α$ ≤180°) and C(180°< $α$ $α$ ≤270°) with the arch foot junction as the center, and the other is that the crack dip angle α is fixed as 127° between the tunnel bottom and the crack, and the ratio of crack length β is different. The disadvantageous factors of the arch foot crack are analyzed by comparing the laboratory test results with the numerical simulation ones, and then green sandstone is chosen to make tunnel model samples to obtain the effect of crack on the stability of the surrounding rock mass. The stress intensity factor at crack tip and the damage evolution nephogram of the surrounding rock mass are calculated by finite element program. The following significant conclusions are drawn: (1) When a crack is located at the tunnel arch foot with different angles of $α$ $α$ , the damage degrees of the tunnel model failure distribution zones can be arranged in a sequence: B>C>A. (2) As the dip angle α ranges from 120°~135°, the stability of the tunnel is the weakest. (3) For a tunnel model sample under biaxial compression loading, the failure modes are mainly the tensile and shear failures at the crack tip and sidewall as well as the tensile failure at vault. (4) The influences of crack on tunnel stability are inversely proportional to the crack length ratio β.
- tunnel /
- crack dip angle /
- numerical simulation /
- arch foot crack /
- surrounding rock mass

HTML全文

0. 引言

软弱层带是在构造作用下形成的较周围岩体显著软弱的断裂构造。其厚度可以是几厘米到几十厘米,延伸长度几十米到几公里不等。由于软弱层带的存在,使得岩体易沿其发生滑动,从而导致岩体的大规模破坏,危及工程建设。因此工程建设过程中,对软弱层带的研究就显得十分重要。国内外已有不少专家学者对层间错动带分布规律、渗透特征及力学性质等进行了深入的研究,并编制了一些技术文件用于指导工程应用^[1-2]。自然界中的软弱层带的起伏程度和粗糙程度可以明显地影响节理的变形和强度特征^[3-4],而且,它们的影响方式和程度还与受力状态密切相关^[5]。同时,含水率对层间错动带也有较大的影响^[6-7],以及伴随有组合体结构效应、弱胶结效应等^[8-9]。在剪切试验方面,蒋宇静讨论了不同边界条件剪切作用下岩石节理力学性能与分形维数变化的关系^[10],巴顿在大量剪切试验的基础上提出JRC-JCS模型^[14]。层间错动带的尺寸效应也是经典难题之一,通过试验方式来研究尺寸效应是最直接最有效的方式之一^[11-15]。然而,对于类似白鹤滩工程的长大层间错动带,起伏波长3～4 m,起伏高度15～20 cm,目前无法开展大尺寸的剪切试验,且原位试验设备复杂、成本昂贵、耗时费力,存在一定的局限性。随着计算机技术的发展,应用数值方法进行尺寸效应的研究应属当下最为可行的方案。

本文研究成果以世界规模最大的金沙江白鹤滩水电站地下洞室群工程为背景,这些广泛分布的软弱层间错动带问题是制约地下洞室群的关键技术问题。针对层间错动带力学参数的取值开展了系统性的研究工作。基于大规模现场和室内试验,获取层间错动带的力学参数,同时引入数字近景摄影测量技术获取层间错动带面壁起伏特征,结合颗粒流法,克服了传统经验方法确定层间错动带力学参数时,无法定量考虑层间错动带粗糙度、软弱充填物厚度和尺寸效应的影响,建立了模拟层间错动带剪切试验模型,获得了粗糙度、软弱充填厚度、尺寸效应的变化导致层间错动带力学参数变化的规律。工程中,层间错动带研究成果用于⑦号尾水调压室的穹顶体形优化。

1. 白鹤滩层间错动带概况

1.1 工程背景

白鹤滩坝区中的许多结构面具有程度不同的起伏特征,根据结构面的规模、性状特征及工程地质意义,参考有关规范,将结构面划分为四级,其中Ⅱ、Ⅲ级又分别划分为两个亚级。其中最典型为层间错动带为Ⅱ₁级（图1）。层间错动带（以“C”表示）是在坝区峨眉山组玄武岩岩流层之间发育的缓倾角构造错动带,自第二岩流层到第十一岩流层共发育11条。其形成为玄武岩岩流层顶部较为软弱的凝灰岩在构造改造过程中发生破碎的凝灰质破碎夹层。由于凝灰质成分对水的敏感性,在地下水的作用下易于软化甚至泥化,其空间展布与岩流层产状近于一致。

图 1 白鹤滩右岸层间错动带分布概况

Figure 1. Distribution of bedding fault zone in Baihetan Hydropower Station

下载: 全尺寸图片幻灯片

层间错动带常分布于每个岩流层的中下部致密玄武岩内,主要走向北东,倾向南东,少量为北西走向,倾角在10°～30°。自预可研勘察以来,经地质测绘、平洞、钻孔揭露,层间错动带有11条,层内错动带有170条。各级错动带均表现为多期活动特征。

早期错动即在燕山期与区域性近南北向褶皱同期形成,显示上盘向上的反向滑动,晚期为上盘向下的正向滑动。在早期区域褶皱过程中,当上覆微晶玄武岩与下伏凝灰岩发生剪切时,最先产生了错动带上下边缘的劈理化带（图2中A处）,指示了错动带早期反向滑移运动；继之产生的是错动带中间的碎裂构造岩（图2中B处）；最后产生的是斜向贯通错动带顶、底界面发育,反映晚期正向滑移运动的断层泥砾或含砾碎粉岩带（图2中C处）。层间错动带的产状平缓,是边坡、坝肩抗力体及地下洞室围岩稳定的控制性结构面^[16],对层间错动带力学特性的研究具有重要意义。

图 2 层间错动带构造岩发育特征示意图^[17]

Figure 2. Development characteristics of structural mineral rock in bedding fault zone^[17]

下载: 全尺寸图片幻灯片

1.2 物理力学试验

对坝区各勘探点及露头的错动带进行了详细的调查、取样和分析工作,对主要的缓倾角错动带进行室内及现场的多种方法测试。白鹤滩坝区共进行现场试验有抗剪试验34组、蠕变试验1组、变形试验水平铅直各9组,渗透试验2组。室内试验有颗粒分析697组,直剪试验223组,物理性质试验273组,渗透试验156组等。现场剪切试验过程遵循《工程岩体试验方法标准》^[19]。

根据室内颗粒分析试验成果统计,坝区层间错动带以岩屑夹泥型最多（如C2、C4）,其次是岩块岩屑型和泥夹岩屑型。根据刚性承压板变形试验统计结果看,无充填型错动带的变形模量相对较高,为4.14 GPa,岩块岩屑型、岩屑夹泥型及泥夹岩屑型错动带变形模量较低,分别为0.24,0.14,0.08 GPa。常规抗剪试验由于每块试件接触面的凸凹情况不同,导致抗剪试验曲线略有差异,为了降低数据离散性对反演分析的影响,选择接触面起伏不大、且抗剪试验曲线理想的试件作为研究对象,以试验屈服强度平均值作为标准值,从统计结果看,Ⅱ₁级和Ⅲ₁级错动带总体上均表现出随性状变好参数提高的趋势,同类型Ⅱ₁级和Ⅲ₁级错动带抗剪强度较接近。由于该强度参数是基于现场剪切试验的成果,是国内规范常用的结构面参数取值方法,但该方法的现场试验尺寸是0.5 m×0.5 m,对于白鹤滩规模巨大的层间错动带,无法考虑其整体波长起伏带来的影响,因此,需结合数值方法进一步对层间错动带的强度参数进行尺寸效应研究。

2. 层间错动带面壁特征统计

手工测量是岩体结构面信息采集较为传统的方法,本文利用数字近景摄影测量技术对层间错动带进行有效信息提取。基于空间射影理论的直接线性变换算法,利用数字化的三维照片,便可以获得结构面的位置、产状、长度和空间分布。通过演绎共线条件方程式,建立像点坐标系与相应空间坐标之间直接的线性关系,方程如下：

$\begin{array}{l} x - x_{0} + Δ x + f \frac{a_{1} (X - X_{s}) + b_{1} (Y - Y_{s}) + c_{1} (Z - Z_{s})}{a_{3} (X - X_{s}) + b_{3} (Y - Y_{s}) + c_{3} (Z - Z_{s})} = 0, \\ y - y_{0} + Δ y + f \frac{a_{2} (X - X_{s}) + b_{2} (Y - Y_{s}) + c_{2} (Z - Z_{s})}{a_{3} (X - X_{s}) + b_{3} (Y - Y_{s}) + c_{3} (Z - Z_{s})} = 0, \end{array}}$

(1)

式中 $Δ x$ , $Δ y$ 为像点坐标纠正值； $a_{i}, b_{i}, c_{i} (i = 1, 2, 3)$ 为像空间坐标系相对此空间坐标系的方向余弦；X,Y,Z为目标点空间坐标；X_s,Y_s,Z_s为摄站点的空间坐标。

由共线方程可得到待定点的误差方程式：

$V = [A : B] [\begin{matrix} t \\ X \end{matrix}] - L$ 。

(2)

用矩阵表示的某一像点的误差方程为

$[\begin{matrix} V_{1} \\ V_{2} \end{matrix}] = [\begin{matrix} A_{1} & 0 & B_{1} \\ 0 & A_{2} & B_{2} \end{matrix}] [\begin{matrix} t_{1} \\ t_{2} \\ X \end{matrix}] - [\begin{matrix} l_{1} \\ l_{2} \end{matrix}]$ 。

(3)

某一像对上的同名点的误差方程为

$V_{1} = {[\begin{matrix} v_{x 1} & v_{y 1} \end{matrix}]}^{T}$ ,

(4)

式中,x,y为以像主点为原点的像点坐标,X,Y,Z为相应的地面点坐标,f为像片主距, $X_{s}, Y_{s},$ $Z_{s}, ϕ, ω, κ$ 为外方位元素。通过绝对控制点或者相对控制点代入共线方程式（通常包括12个数据）,求出像片的外方位元素和所求点的坐标。通过三维网格将这些像点串联起来,形成三维数据化地形模型（即DTM模型）,便可以通过解译提取选区内所需要的相关数据。

2.1 面壁三维信息整体解决方案

通过对现场的多次查勘,由于C4延伸范围较大,选择了典型特征露头区域（图3）,开展三维数码拍摄工作。为获得较好的解译精度,现场对所选区域内部的水进行处理和杂草进行了铲除,同时架设了一个约2 m高的台架进行拍摄工作,每个区域同时布置3个站点,成果选取匹配度较好的两站进行模型生成并解译。

图 3 层间错动带C4典型露头区摄影取样（24 mm镜头成像）

Figure 3. Photographic sampling of typical outcrop area A2 in bedding fault zone C4

下载: 全尺寸图片幻灯片

工作所选区域生成的模型精度（即均方差）较高,达到毫米级,可以用于结构面起伏度的测量工作。根据各区域内包体分布情况,考虑剖面分布尽量通过最多的包体顶点,剖面还分别从两个不同方向进行切割,保证能够量测到各区域内最大起伏高度值,量测时均在三维模型空间下操作,为此,实际量测的长度和高度均为实际值。

2.2 面壁起伏特征统计

综合典型露头区域测量统计结果,区域包体间起伏波长长度主要分布在2.0～3.0 m（图4）,起伏波长长度应用时可取其平均值2.5 m；区域包体间起伏高度应用时可考虑选取10～25 cm（图5）3个统计分段平均值的加权平均值,即17.05 cm,而全部起伏高度平均值为17.54 cm,分段平均值的加权平均值可作为可靠的统计应用结果。

图 4 C4统计区结构面起伏波长分布统计

Figure 4. Statistics of fluctuation wavelength distribution of structural plane in C4

下载: 全尺寸图片幻灯片

图 5 C4统计区结构面起伏高度分布统计

Figure 5. Statistics of undulation height distribution of structural plane in C4

下载: 全尺寸图片幻灯片

3. 基于PFC层间错动带数值试验

无论是试验方法还是经验方法,均难以定量获得层间错动带力学性质随着考察尺寸增大的变化特征,本节采用数值方法针对层间错动带开展数值试验研究。根据现场试验所获得的层间错动带充填物的岩体力学参数,采用颗粒流方法根据现场数码照相技术获得的层间错动带面壁起伏特征开展层间错动带中粗糙度、软弱充填物厚度、及尺寸因素对错动带力学参数的定量影响。

3.1 相关影响因素敏感性分析

本节在参考Cundall^[20]研究方法与成果的基础上,采用CPM模型进行岩石结构面剪切力学行为的颗粒流数值模拟研究^[21]。模型介质重现岩土材料的宏观力学响应并不容易,其中的PFC细观参数标定过程需要进行一系列与室内试验或现场条件类似的模型试验,并将模型试件的宏观力学响应与室内试验或原位测试结果进行对比,通过试错法反复矫正^[22],直到模型介质的宏观力学响应满足要求为止,该标定工作不在本文赘述。粗糙度敏感性分析以层间错动带反演分析为基础,分别考虑4组不同的粗糙度系数（JRC）,即JRC=2～4,8～10,10～12,18～20,以此来研究不同粗糙度系数对C4层间错动带强度参数的影响。针对不同的粗糙度需要单独建立相应的模型,以实施剪切试验。图6是不同粗糙度系数所对应的层间错动带参数统计,综合计算结果可以发现,即便层间错动带的充填厚度达到20 cm,粗糙度仍然对力学参数具有一定的影响,从定性角度：①层间错动带摩擦角随着粗糙度系数的增大而呈现增大趋势；②层间错动带黏聚力随着粗糙度系数的增大而呈现减小趋势。针对C4的数码照相成果可以知道,层间错动带的粗糙度一般在8～12变化,因此可以认为对于C4这一类泥夹岩屑型的层间错带动带,粗糙度的变化可以导致摩擦角发生27%左右的变化,黏聚力发生11%左右的变化。

图 6 不同粗糙度系数的层间错动带强度参数影响

Figure 6. Influences of strength parameters in bedding fault zone with different roughness coefficients

下载: 全尺寸图片幻灯片

针对层间错动带充填厚度,分别对10,15,20 cm的厚度开展数值分析工作,3种不同粗糙度条件下,针对JRC=8～10,10～12,18～20这3种粗糙度情形,开展法向压力为0.6,0.9,1.2,1.5 MPa条件下的直剪试验。所对应的充填厚敏感性分析的计算模型图7所示。

图 7 不同层间错动带厚度的数值模型（JRC=10~12）

Figure 7. Numerical model for thickness of different bedding fault zone (JRC=10~12)

下载: 全尺寸图片幻灯片

表1为不同粗糙度系数及不同充填厚度所对应的层间错动带参数统计,当错动带物质的软弱充填厚度超过10 cm后,随着充填厚度的增大,摩擦角普遍呈降低趋势,而黏聚力变化不大。以结构面粗糙度系数JRC=10～12的数值试验结果为例,当层间错动带结构面厚度分别取10,15,20 cm时,层间错动带结构面摩擦角分别为20.32°,18.34°,15.21°,而层间错动带结构面黏聚力分别为0.051,0.052,0.056 MPa。对于C4这种泥夹岩屑型的层间错动带来说,随着厚度的增加,摩擦系数迅速降低,而黏聚力逐渐上升,但黏聚力的影响甚微。

表 1 不同充填物厚度强度参数值计算结果

Table 1. Calculated results of strength parameters in numerical tests with different filling thicknesses

粗糙度系数	层间错动带厚度/cm	摩擦角/(°)	黏聚力/MPa
8~10	10	19.29	0.054
	15	17.74	0.060
	20	14.80	0.062
10~12	10	20.32	0.051
	15	18.34	0.052
	20	15.21	0.056
18~20	10	22.08	0.050
	15	20.42	0.052
	20	16.84	0.054

下载: 导出CSV

| 显示表格

3.2 层间错动带尺寸效应研究

同样,对于尺寸效应对力学参数的影响研究,根据三维数码照相的成果,采用离散元颗粒流法生成不同尺寸直剪试验试样,试样尺寸涵盖0.5 m×0.5 m,1.0 m×1.0 m,2.0 m×2.0 m,4.0 m×4.0 m,8.0 m×8.0 m这5组不同尺度,在相同粗糙度系数JRC和相同软弱充填厚度的前提下,模拟不同法向压力条件下的剪切试验,法向压力包括4个等级,即0.6,0.9,1.2,1.5 MPa,如图8所示。

图 8 不同几何尺寸的错动带抗剪数值试验模型

Figure 8. Numerical shear test models with different geometrical sizes

下载: 全尺寸图片幻灯片

总体上,随着试验尺寸的增大,黏聚力和摩擦角呈降低趋势,并趋于平稳。当层间错动带的试验尺寸在2 m以内时,黏聚力和摩擦角的变化比较明显,当层间错动带的试验尺寸达到4 m时,黏聚力和摩擦角趋于稳定,可以认为泥夹岩屑型层间错动带代表REV尺寸为4 m；引入考虑尺寸效应后,当试验尺寸由0.5 m增大至8 m时,摩擦角由14.88°降低为12.56°,降低幅度15.6%；黏聚力由0.062 MPa降低至0.030 MPa,降低幅度51.6%,相关拟合公式分别如图9,10所示。

图 9 不同试件尺寸与摩擦角影响

Figure 9. Influences of friction angle with different specimen sizes

下载: 全尺寸图片幻灯片

图 10 不同试件尺寸与黏聚力影响

Figure 10. Influences of cohesion with different specimen sizes

下载: 全尺寸图片幻灯片

4. 层间错动带研究成果应用

白鹤滩坝址区及地下洞室群共发育11条大规模的层间错动带,作为主体工程的坝基边坡、地下厂房都不同程度受到层间错动带的影响,对于地下厂房洞室群而言,可以说层间错动带制约着厂房围岩稳定和破坏。尾水调压室穹顶开挖体形变化对枢纽布置、开挖工程量、水力条件等影响甚小,不同体形的尾水调压室穹顶施工方案无本质区别,因此围岩稳定条件是局部体形选择最为关键的控制性因素。推荐采用圆筒形方案,其穹顶具备“双向”成拱的特征,可以显著改善长廊形尾调室顶拱受力条件和边墙变形状态。

在白鹤滩特定的地应力场和岩体结构条件下,圆筒形尾调穹顶围岩仍然受到高应力和不利构造（如层间带和柱状节理等）的作用,加之尾调室本身规模宏大（开挖跨度达50 m）,所以,尾调室穹顶稳定仍然是白鹤滩地下工程建设面临的挑战之一。通过尾调室体形方案比选后,针对层间错动带C4斜切⑦号尾调室穹顶侧翼部位,其穹顶稳定性受层间错动带C4影响非常之大,需调整合适的形状来满足工程安全开挖的需求。图11为⑦号尾调室3种顶拱优化比选。从应力分布来看,半圆形、椭圆形穹顶应力集中程度基本相当,相比圆弧形增大2～3 MPa。从变形来看,3种体形穹顶变形量值和差异均不大,两翼变形较大,相比圆弧形和半圆形体形,椭圆形穹顶南侧侧翼C4下盘岩体变形较大,增大约30%～110%。从塑性区深度看,圆弧形、半圆形和椭圆形体形的穹顶塑性区深度总体相差不大,但在层间错动带C4切割S侧部位的塑性区深度有一定差异。相关优化参数对比如表2所示。因此,由于层间错动带的影响,曲率较大的椭圆形体形不利于控制两翼的松弛问题,圆弧形、半圆形体形总体差异不大。综合穹顶围压及拱肩部位体形过渡考虑,⑦号尾水调压室穹顶采用半圆形体形。

图 11 ⑦号尾调室顶拱方案比选

Figure 11. Comparison of dome shapes of No.7 tailrace surge chamber

下载: 全尺寸图片幻灯片

表 2 ⑦号尾水调压室不同体形开挖响应特征汇总表

Table 2. Summary of excavation response characteristics of No. 7 tailrace surge chamber with different dome shapes

定量指标	部位		圆弧形	半圆形	椭圆形
最大变形量级/mm	穹顶位移		16~18	13~15	11~14
	C4上盘	E/W侧翼	14~21	13~22	13~21
	C4上盘	N/S侧翼	25~30	16~28	15~28
	C4下盘	E/W侧翼	40~83	40~75	41~81
	C4下盘	N/S侧翼	33~76	34~121	39~159
应力分布 $σ_{1}$ /MPa	穹顶应力集中		34.1	36.4	36.8
	C4下盘	E/W侧翼松弛	18.7	15.7	15.5
	C4下盘	N/S侧翼松弛	15.8	12.6	10.3
$σ_{3}$ /MPa	C4下盘拉应力		+0.17	+0.19	+0.26
塑性区深度/m		C4下盘	5.6	6.2	9.2

下载: 导出CSV

| 显示表格

5. 结论

本文对白鹤滩层间错动带力学参数的取值开展了系统性的研究工作,通过引入数字近景摄影测量技术结合颗粒流数值方法对层间错动带进行尺寸效应分析,研究成果应用于工程实际。

（1）白鹤滩坝区自第二岩流层到第十一岩流层共发育11条层间错动带,具有规模大、贯穿性强等特点,在围岩稳定中起关键控制性作用。结合现场试验,初步得到层间错动带C4的力学强度参数。

（2）引入数字近景摄影测量技术对层间错动带C4典型露头进行统计测量,相比传统经验估值,较为精准地获取层间错动带C4的面壁起伏特征。

（3）结合获取的面壁起伏特征,采用颗粒流对层间错动带进行相关敏感性分析：层间错动带摩擦角随着粗糙度系数的增大而呈现增大趋势；层间错动带黏聚力随着粗糙度系数的增大而呈现减小趋势；同时受填充厚度影响,当层间错动带的充填厚度超过10 cm后,随着充填厚度的增大,摩擦角普遍呈降低趋势,而黏聚力变化不大；引入尺寸效应后,摩擦角和黏聚力均随着尺度增大而相应减小,并趋于平稳。

（4）白鹤滩地下厂房洞室群开挖过程中,结合前期层间错动带研究成果。对处于层间错动带C4的⑦号尾水调压室穹顶进行体形优化,由此证明半圆形穹顶体形更适应于开挖应力成拱条件,且有利于侧翼应力平顺过渡,同时针对性地评估了层间错动带对影响部位的围岩稳定,并为后续开挖方案决策提供了技术支撑。

图 1 裂纹分布示意图

Figure 1. Sketch map of crack distribution

下载: 全尺寸图片幻灯片

图 2 隧道模型试样

Figure 2. Tunnel model specimens

下载: 全尺寸图片幻灯片

图 3 试验模型加载设备

Figure 3. Model test loading devices

下载: 全尺寸图片幻灯片

图 4 模型试件加载的应力-应变时程曲线

Figure 4. Stress-strain curves of cracked tunnel specimens

下载: 全尺寸图片幻灯片

图 5 裂纹倾角 $α$ $α$ 与试件峰值应力的变化趋势线

Figure 5. Strength history of the tunnel model specimens with crack dip angle $α$ $α$

下载: 全尺寸图片幻灯片

图 6 裂纹长度比 $β$ $β$ 与试件峰值应力的变化趋势线

Figure 6. Variation of strength of tunnel model specimens with crack length ratio $β$ $β$

下载: 全尺寸图片幻灯片

图 7 裂纹倾斜角 $α$ $α$ 下的声发射图与最大主应力云图

Figure 7. Diagrams of acoustic emission and clouds of shear stress of crack dip angle $α$ $α$

下载: 全尺寸图片幻灯片

图 8 隧道试件有限元模型

Figure 8. Finite element model for tunnel specimen

下载: 全尺寸图片幻灯片

图 9 隧道模型的最大主应力云图、试验照片及数值损伤分布图

Figure 9. Clouds and test photos of maximum principal stress and distribution map of numerical damage

下载: 全尺寸图片幻灯片

图 10 K_I、K_II值随裂纹倾角 $α$ $α$ 变化趋势线

Figure 10. Trendline of stress intensity factor with crack angle $α$ $α$

下载: 全尺寸图片幻灯片

图 11 K_I、K_II值随裂纹长度比 $β$ $β$ 变化趋势线

Figure 11. Variation of stress intensity factor with crack length ratio $β$ $β$

下载: 全尺寸图片幻灯片

参考文献(32)

[1]	CHU B L, HSU S C, CHANG Y L, et al. Mechanical behavior of a twin-tunnel in multi-layered formations[J]. Tunnelling and Underground Space Technology, 2007, 22(3): 351-362. doi: 10.1016/j.tust.2006.06.003
[2]	WANG S Y, SLOAN S W, SHENG D C, et al. Numerical study of failure behaviour of pre-cracked rock specimens under conventional triaxial compression[J]. International Journal of Solids and Structures, 2014, 51(5): 1132-1148. doi: 10.1016/j.ijsolstr.2013.12.012
[3]	ZHOU X, QIAN Q, YANG H. Rock burst of deep circular tunnels surrounded by weakened rock mass with cracks[J]. Theoretical and Applied Fracture Mechanics, 2011, 56(2): 79-88. doi: 10.1016/j.tafmec.2011.10.003
[4]	郭东明, 闫鹏洋, 杨仁树, 等. 爆破开挖中巷道围岩缺陷扩展的动焦散模型试验研究[J]. 采矿与安全工程学报, 2015, 32(5): 728-734. doi: 10.13545/j.cnki.jmse.2015.05.005 GUO Dong-ming, YAN Peng-yang, YANG Ren-shu, et al. Dynamic caustics model experimental study on the defects extension of roadway surrounding rock when blasting excavation[J]. Journal of Mining and Safety Engineering, 2015, 32(5): 728-734. (in Chinese) doi: 10.13545/j.cnki.jmse.2015.05.005
[5]	杨忠民, 高永涛, 吴顺川, 等. 节理岩体中纵向间距对连拱隧道稳定性的影响[J]. 中国公路学报, 2018, 31(10): 167-176. doi: 10.3969/j.issn.1001-7372.2018.10.016 YANG Zhong-min, GAO Yong-tao, WU Shun-chuan, et al. Influence of longitudinal spacing of double-arch tunnel on tunnel stability in jointed rock mass[J]. China Journal of Highway and Transport, 2018, 31(10): 167-176. (in Chinese) doi: 10.3969/j.issn.1001-7372.2018.10.016
[6]	JIA P, TANG C. Numerical study on failure mechanism of tunnel in jointed rock mass[J]. Tunnelling and Underground Space Technology, 2008, 23(5): 500-507. doi: 10.1016/j.tust.2007.09.001
[7]	LI X, LEI W. Numerical investigation on fracturing behaviors of deep-buried opening under dynamic disturbance[J]. Tunnelling and Underground Space Technology, 2016, 54: 61-72. doi: 10.1016/j.tust.2016.01.028
[8]	ZHU Z, LI Y, XIE J, et al. The effect of principal stress orientation on tunnel stability[J]. Tunnelling and Underground Space Technology, 2015, 49: 279-286. doi: 10.1016/j.tust.2015.05.009
[9]	LIU J P, LI Y H, XU S D, et al. Cracking mechanisms in granite rocks subjected to uniaxial compression by moment tensor analysis of acoustic emission[J]. Theoretical and Applied Fracture Mechanics, 2015, 75(6): 151-159.
[10]	CHEN S Z. The application of fracture mechanics in highway tunnel lining cracking[J]. Applied Mechanics and Materials, 2014, 580: 1377-1381.
[11]	PARK S W, PARK S S, HWANG I B, et al. A case study on cause analysis for longitudinal crack of duct slab in tunnel[J]. Journal of the Korea institute for structural maintenance and inspection, 2012, 16(5): 19-28. doi: 10.11112/jksmi.2012.16.5.019
[12]	SUN X, QIANG Y, ZHAO M J, et al. Research on fractal crack propagation mechanism of hydraulic tunnel concrete lining[J]. Applied Mechanics and Materials, 2013, 353: 1704-1708.
[13]	WANG N, CHEN P H, WANG J C, et al. Crack propagation detection and simulation research of Jiulong tunnel[J]. Advanced Materials Research, 2012,446: 2256-2261.
[14]	ZHU Z, WANG L, MOHANTY B, et al. Stress intensity factor for a cracked specimen under compression[J]. Engineering Fracture Mechanics, 2006, 73(4): 482-489. doi: 10.1016/j.engfracmech.2005.08.008
[15]	HAERI H, MARJI M F, SHAHRIAR K. Simulating the effect of disc erosion in TBM disc cutters by a semi-infinite DDM[J]. Arabian Journal of Geosciences, 2015, 8(6): 3915-3927. doi: 10.1007/s12517-014-1489-5
[16]	FAN Y, ZHU Z, ZHAO Y, et al. The effects of some parameters on perforation tip initiation pressures in hydraulic fracturing[J]. Journal of Petroleum Science and Engineering, 2019, 176: 1053-1060. doi: 10.1016/j.petrol.2019.02.028
[17]	WANG M, ZHU Z M, LIU J H. The photoelastic analysis of stress intensity factor for cracks around a tunnel[J]. Applied Mechanics and Materials, 2012, 142: 197-200.
[18]	FAN Y, ZHAO Y, ZHU Z, et al. Stress intensity factors for a tunnel containing a radial crack under compression[J]. Advances in Mechanical Engineering, 2017, 9(12): 1-14.
[19]	康勇, 李晓红, 杨春和. 深埋隧道围岩损伤破坏模式的数值试验研究[J]. 岩石力学与工程学报, 2007, 26(增刊1): 3578-3583. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2007S1151.htm KANG Yong, LI Xiao-hong, YANG Chun-he. Numerical tests of damage failure mode of surrounding rock damage in deep tunnels[J]. Journal of Rock Mechanics and Engineering, 2007, 26(S1): 3578-3583. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2007S1151.htm
[20]	李元鑫, 朱哲明, 刘凯, 等. 裂纹方向对隧道稳定性影响规律的研究[J]. 岩土力学, 2014, 35(增刊1): 189-194. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S1026.htm LI Yuan-xin, ZHU Zhe-ming, LIU Kai, et al. Study of effect of cracking orientation on tunnel stability[J]. Rock and Soil Mechanics, 2014, 35(S1): 189-194. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S1026.htm
[21]	周磊, 朱哲明, 刘邦. 隧道周边不同位置径向裂纹对隧道围岩稳定性影响规律的研究[J]. 岩土工程学报, 2016, 38(7): 1230-1237. ZHOU Lei, ZHU Zheming, LIU Bang. Influence of radial cracks on stability of surrounding rocks at different locations around tunnel[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1230-1237. (in Chinese)
[22]	ZHANG L F, YI Z L, DENG Y J. The crack limit analysis based on the fracture mechanics of the main arch of the stone arch bridge[J]. Applied Mechanics and Materials, 2013, 361: 1155-1159.
[23]	ZHOU L, ZHU Z, LIU B, et al. The effect of radial cracks on tunnel stability[J]. Geomechanics and Engineering, 2018, 15(2): 721-728.
[24]	周磊, 朱哲明, 刘邦. 裂纹对直墙拱形隧道围岩损伤破坏模式的影响规律研究[J]. 岩土力学, 2017, 38(12): 3688-3697. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201712038.htm ZHOU Lei, ZHU Zhe-ming, LIU Bang. Influence of cracks on surrounding rock damage-failure mode of straight wall arch tunnel[J]. Rock and Soil Mechanics, 2017, 38(12): 3688-3697. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201712038.htm
[25]	徐志英. 岩石力学[M]. 3版.北京: 中国水利电力出版社, 2007. XU Zhi-ying. Rock Mechanics[M]. 3rd ed. Beijing: China Water Power Press, 2007. (in Chinese)
[26]	NIU L, ZHU W, ZHEN C, et al. Numerical simulation on excavation-induced damage of rock under quasi-static unloading and dynamic disturbance[J]. Environmental Earth Sciences, 2017,76(17): 1-14.
[27]	WANG Q, ZHU W, XU T, et al. Numerical simulation of rock creep behavior with a damage-based constitutive law[J]. International Journal of Geomechanics, 2016, 17(1): 1-14.
[28]	ZUO Y, ZHANG Q, XU T, et al. Numerical tests on failure process of rock particle under impact loading[J]. Shock and Vibration, 2015: 1-12.
[29]	WANG Q Z, YANG J R, ZHANG C G, et al. Sequential determination of dynamic initiation and propagation toughness of rock using an experimental-numerical-analytical method[J]. Engineering Fracture Mechanics, 2015, 141: 78-94.
[30]	WEN H, DONG S, YANG F, et al. Investigation on the correlation of mode II fracture toughness of sandstone with tensile strength[J]. Engineering Fracture Mechanics, 2017, 184: 249-258.
[31]	XU Y, DAI F, ZHAO T, et al. Fracture toughness determination of cracked chevron notched Brazilian disc rock specimen via griffith energy criterion incorporating realistic fracture profiles[J]. Rock Mechanics and Rock Engineering, 2016, 49(8): 3083-3093.
[32]	李地元, 韩震宇, 孙小磊, 等. 含预制裂隙大理岩SHPB动态力学破坏特性试验研究[J]. 岩石力学与工程学报, 2017, 36(12): 2872-2883. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201712002.htm LI Di-yuan, HAN Zheng-yu, SUN Xiao-lei, et al. Characteristics of dynamic failure of marble with artificial flaws under split Hopkinson pressure bar tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(12): 2872-2883. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201712002.htm

施引文献(3)

期刊类型引用(2)

1.	范雷，余美万，邬爱清，向前. 层间错动带水力耦合抗剪强度特性演化规律研究. 岩土力学. 2023(07): 1959-1970 . 百度学术
2.	武倩宇，韩登林，张吉振，王晨晨，任晓海，林珍珍，苏苗苗，朱亚玲，张娟. 页岩储层中颗粒尺寸效应对微裂缝发育的影响：以威远地区志留系龙马溪组页岩储层为例. 中南大学学报(自然科学版). 2022(09): 3603-3614 . 百度学术

其他类型引用(1)

资源附件(0)

图(11)

计量

文章访问数:
HTML全文浏览量: 0
PDF下载量:
被引次数: 3

0. 引言
1. 白鹤滩层间错动带概况
1.1 工程背景
1.2 物理力学试验
2. 层间错动带面壁特征统计
2.1 面壁三维信息整体解决方案
2.2 面壁起伏特征统计
3. 基于PFC层间错动带数值试验
3.1 相关影响因素敏感性分析
3.2 层间错动带尺寸效应研究
4. 层间错动带研究成果应用
5. 结论

0. 引言
1. 白鹤滩层间错动带概况
1.1 工程背景
1.2 物理力学试验
2. 层间错动带面壁特征统计
2.1 面壁三维信息整体解决方案
2.2 面壁起伏特征统计
3. 基于PFC层间错动带数值试验
3.1 相关影响因素敏感性分析
3.2 层间错动带尺寸效应研究
4. 层间错动带研究成果应用
5. 结论

参考文献(32)

施引文献(3)

资源附件(0)

马蹄形隧道拱脚裂纹对围岩稳定性的影响 English Version

作者简介: 周磊（1990— ）,男,博士,助理研究员,主要从事岩石断裂力学的研究工作。E-mail：zhouleittkx@126.com

通讯作者: 朱哲明, E-mail：zhemingzhu@hotmail.com

计量

出版历程