堆载作用下土体分层特性对地铁隧道纵向变形的影响研究

梁发云; 袁强; 李家平; 张少夏

doi:10.11779/CJGE202001007

堆载作用下土体分层特性对地铁隧道纵向变形的影响研究 English Version

1.
同济大学地下建筑与工程系,上海200092
2.
上海申通地铁集团有限公司,上海200070

基金项目:

上海申通地铁集团有限公司科研计划项目 JS-KY18R022-3

详细信息

作者简介:
梁发云（1976— ）,男,博士,教授,主要从事土力学与基础工程的教学科研工作。E-mail：fyliang@tongji.edu.cn

中图分类号: TU473
计量
- 文章访问数: 427
- HTML全文浏览量: 32
- PDF下载量: 327
出版历程
- 收稿日期: 2019-05-08
- 网络出版日期: 2022-12-07
- 刊出日期: 2019-12-31

Influences of soil characteristics on longitudinal deformation of shield tunnels induced by surface surcharge

1.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
2.
Shanghai Shentong Metro Group, Shanghai 200070, China

摘要

摘要: 随着城市化进程的不断推进,地铁隧道附近可能会出现不同形式的地表堆载,将对地铁隧道的健康状态产生不利影响。现有的方法多是基于Boussinesq解求解地表堆载引起的附加应力,无法考虑土体的分层特性。首先采用Fourier积分变换得到了直角坐标系中竖向荷载作用下层状地基附加应力的基本解；然后将下卧隧道视为Timoshenko梁,基于Winkler地基模型和两阶段法求得隧道纵向位移和内力。为考察地基土成层性对既有隧道性状的影响,对上软下硬、上硬下软两种典型层状地基中的隧道进行了参数分析。结果表明：地基土成层特性对隧道形状影响比较大,相比而言,隧道下卧土层控制沉降的效果要优于隧道上覆土层。
- 地表堆载 /
- 层状地基 /
- 地铁隧道 /
- 隧道变形 /
- 两阶段法
Abstract: With the development of urbanization in China, it is common to find the surface surcharge in a large scale around the metro tunnels, which will seriously threaten the safety of the lining structures and their service capability. To obtain the additional stress on the axis of shield tunnels caused by the surface surcharge, the Boussinesq’s solution is widely adopted, whereas it cannot be applied in multi-layered soils. In this study, firstly, the additional stress in multi-layered soils is obtained by using the Fourier integral transformation. Secondly, the existing tunnel is regarded as the Timoshenko beam, and the displacements and internal forces exerted on the shield tunnel are obtained based on the two-stage method. From the proposed method, it can be found that the underlying layer has larger influences on the settlement of shield tunnels than those by the overlying soils.
- surface surcharge /
- multi-layered soil /
- shield tunnel /
- deformation of tunnel /
- two-stage method

HTML全文

0. 引言

近年来,城市轨道交通以其便捷快速的优点在许多城市得到快速的发展。然而随着城市化进程的不断推进,许多已建成的地铁隧道附近不可避免地受到外部工程活动扰动影响,其中突发地表堆载引发的隧道变形事故日益突出^[1],如为便于上海嘉闵高架的施工将河道作为堆放材料场地引起地铁9号线产生较大的不均匀沉降^[2]以及违规弃土引起的地铁正上方堆载导致隧道的横向变形^[3-4]等。地表堆土荷载作用引起的附加应力,会破坏盾构结构原有的平衡状态,引起隧道应力重分布,产生一定的纵向和横向变形,一旦结构内力超过混凝土和螺栓容许应力,会引发管片压损或开裂等^[5],对地铁安全造成严重影响。因此研究地表堆载对临近运营地铁盾构隧道的影响具有重要意义。

目前,已有学者对地表堆载荷载作用下盾构隧道的纵向变形进行了研究。戴宏伟等^[6]利用Boussinesq解和分层总和法计算自由场的位移,基于Euler-Bernoulli梁模型研究了地表施工荷载对临近地铁隧道的影响,但未考虑土体成层特性和隧道自身的结构特性；魏新江等^[7]、魏纲等^[8]基于变分法研究了堆载对下卧隧道错台变形的影响,康成等^[9]采用Timoshenko梁模型研究了不同堆载形式对隧道纵向变形的影响,高继锦等^[10]研究了堆载对下卧交叉隧道竖向位移的影响,但是他们的研究忽略了土体的成层特性；李俊昱等^[11]根据层状弹性半空间理论计算了高填方堆载对地埋管线受力和变形的影响,研究成果虽然涉及到土体的成层特性但没有考虑管线接头的影响。综上,这些研究成果或考虑的土层单一,不能分析土层特性对隧道变形的影响；或忽略了隧道接头引起的隧道整体刚度的弱化,无法准确反映分层地基中堆载对隧道纵向变形的影响。黄大维等^[3]、张明告等^[12]、Zhang等^[13]、张治国等^[14]研究表明当土层性质差别比较大时,不能简单地将分层地基等效为均值地基,关于这一点,康成等^[9]也明确指出。

在实际工程中,由于土是长期自然沉积形成的,因此天然地基并非是均质的弹性体,而是层状分布。基于层状弹性半空间理论^[15-16],本文建立了层状地基中地表堆载对既有隧道影响的弹性分析方法。利用Fourier变换,首先推导了直角坐标系下非均质土体中堆载引起的附加应力；基于两阶段法^[17],采用Timoshenko梁模型和Winkker地基模型,计算地表堆载下隧道的响应；进一步分析上覆土层和下卧土层对隧道内力和变形的影响。与已有的研究成果相比,本文的计算模型可以同时考虑土体的分层特性及隧道的结构特性,通用性更强。

1. 计算模型

1.1 直角坐标系下弹性层状半空间体系基本解

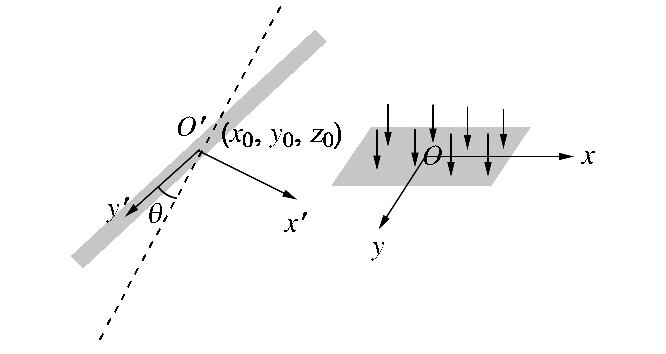
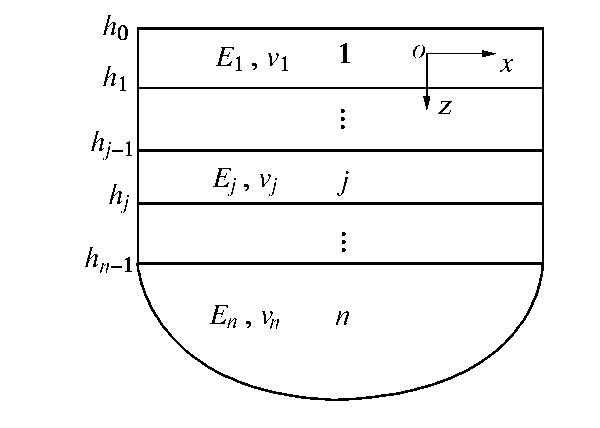
地表堆载作用下将在地层中产生附加应力,从而引起已有地铁隧道产生沉降变形,甚至影响隧道的正常运营。为简化计算,得到堆载下分层地基中的基本解,本文计算模型做如下假定：①地基由多个具有有限厚度的水平层以及半无限空间体组成,每层都是均匀、连续、各向同性的弹性体（如图1所示）；②各层之间弹性接触,且不发生相对滑动；③不考虑土体固结和蠕变以及地表堆载随时间的变化,且堆载前隧道变形已经稳定。

图 1 层状地基示意图

Figure 1. Cross section of multi-layered soils

下载: 全尺寸图片幻灯片

从弹性力学中不计体力的平衡微分方程、几何方程和物理方程构造如下控制方程^[18]：

(1)

式中, $σ_{z}$ , $τ_{z x}$ , $τ_{y z}$ 分别为竖向应力和剪应力, $u_{x}$ , $u_{y}$ , $u_{z}$ 分别为3个方向的位移。

为推导方便,采用如下变换：

\begin{matrix} χ_{1} = \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y}, Γ_{1} = \frac{\partial u_{x}}{\partial x} + \frac{\partial u_{y}}{\partial y}, χ_{2} = \frac{\partial τ_{x z}}{\partial y} - \frac{\partial τ_{y z}}{\partial x}, \\ Γ_{2} = \frac{\partial u_{x}}{\partial y} - \frac{\partial u_{y}}{\partial x} 。 \end{matrix}

(2)

双重Fourier变换与逆变换采用如下形式进行：

\begin{matrix} ({\tilde{χ}}_{1}, {\tilde{Γ}}_{1}, {\tilde{σ}}_{z}, {\tilde{u}}_{z}, {\tilde{χ}}_{2}, {\tilde{Γ}}_{2}) = \frac{1}{4 π^{2}} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} (χ_{1}, Γ_{1}, σ_{z}, u_{z}, χ_{2}, Γ_{2}) \cdot \\ e^{- i (f_{x} x + f_{y} y)} d x d y, \end{matrix}

(3a)

\begin{matrix} (χ_{1}, Γ_{1}, σ_{z}, u_{z}, χ_{2}, Γ_{2}) = \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} ({\tilde{χ}}_{1}, {\tilde{Γ}}_{1}, {\tilde{σ}}_{z}, {\tilde{u}}_{z}, {\tilde{χ}}_{2}, {\tilde{Γ}}_{2}) \cdot \\ e^{i (f_{x} x + f_{y} y)} d f_{x} d f_{y} 。 \end{matrix}

(3b)

$f_{x}$ 和 $f_{y}$ 分别对应于时域中的x和y坐标。结合式（2）,对控制方程（1）进行双重Fourier变换,并写成矩阵形式,有

\frac{d {\tilde{U}}_{I 1}}{d z} = A_{I 1} {\tilde{U}}_{I 1}

(4a)

\frac{d {\tilde{U}}_{I 2}}{d z} = A_{I 2} {\tilde{U}}_{I 2}

(4b)

式中, $f = \sqrt{f_{x}^{2} + f_{y}^{2}}$ , ${\tilde{U}}_{I 1} = {[\begin{matrix} {\tilde{Γ}}_{1} & {\tilde{u}}_{z} & {\tilde{χ}}_{1} & {\tilde{σ}}_{z} \end{matrix}]}^{T}$ ,

\begin{array}{l} {\tilde{U}}_{I 2} = {[\begin{matrix} {\tilde{Γ}}_{2} & {\tilde{χ}}_{2} \end{matrix}]}^{T} \\ A_{I 1} = [\begin{matrix} 0 & f^{2} & \frac{2 (1 + μ)}{E} & 0 \\ - \frac{μ}{1 - μ} & 0 & 0 & \frac{(1 + μ) (1 - 2 μ)}{(1 - μ) E} \\ \frac{E}{1 - μ^{2}} f^{2} & 0 & 0 & \frac{1}{1 - μ^{2}} f^{2} \\ 0 & 0 & - 1 & 0 \end{matrix}], \\ A_{I 2} = [\begin{matrix} 0 & \frac{2 (1 + μ)}{E} \\ \frac{E}{2 (1 + μ)} f^{2} \end{matrix}] 。 \end{array}

依据Cayley-Hamilton定理,对矩阵方程式（4a）,（4b）进行求解可以得到单层地基中应力和位移的传递函数,传递函数的具体表达形式参见文献[18],由于篇幅限制,本文不再赘述。采用与文献[16]相似的处理方式,就可以得到堆载作用下层状土体的应力位移关系：

(5)

基于文献[19]的方法,对式（5）进行双重Fourier逆变换,可以得到真实空间域中地表堆载引起的附加应力数值解。

对于如图2所示的地面偏心堆载,采用如式（6）的坐标变换,并代入式（5）中,即可以得到偏心荷载下分层地基中应力和位移的响应。

\begin{array}{l} x = x^{'} \cos θ - y^{'} \sin θ + x_{0}, \\ y = x^{'} \sin θ + y^{'} \cos θ + y_{0}, \\ z = z_{0} 。 \end{array}}

(6)

图 2 偏心堆载

Figure 2. Eccentric surcharge

下载: 全尺寸图片幻灯片

1.2 地表荷载作用下盾构隧道变形计算

通过1.1节可以得到地表堆载下分层地基中任一深度处附加应力的计算结果,接下来采用两阶段法^[17],计算地铁隧道与土体的相互作用,分析地表堆载下隧道的纵向变形响应。

（1）土体模型

在结构与土体的相互作用计算中,通常采用Winkler地基模型^{[17, 20]}、Pasternak地基模型^[21]、连续弹性体模型来模拟软土^[13]。Liang等^[21-22]分析了基坑开挖对下卧地铁的影响,土体分别采用Winkler地基模型和Pasternak地基模型进行模拟,研究表明两种地基模型下得到的隧道隆起量差别不大,但Winkler地基模型更方便于工程应用。因此,本文土体模型采用Winkler地基模型。关于地基反力系数,Vesic基于地表弹性地基梁,给出了确定地基反力系数的经验公式。由于没有考虑土层埋深对土层刚度的影响,Vesic经验公式会高估了隧道的变形。为了更好地反映埋深对土层刚度的影响,Liang等^[21]提出了基于埋深修正的Vesic地基反力系数经验公式：

k = \frac{1.3 E_{s}}{η B (1 - μ^{2})} \sqrt[12]{\frac{E_{s} B^{4}}{E I}},

(7)

式中, $η = 1 + \frac{1}{1.7 z_{0} / B}$ ^[20], $E_{s}$ , $μ$ 分别为隧道周围土体变形模量和泊松比,B为隧道外径, $E I$ 取隧道等效抗弯刚度 $E I_{eq}$ 。

（2）隧道模型

城市地铁隧道通常由预制管片组成,管片与管片之间通过高强螺栓连成一个整体。毫无疑问,管片接头的存在会削弱盾构隧道的整体刚度。大量监测数据表明,隧道沿轴线方向的变形可以分解为两部分：①弯曲引发管片的弯曲变形,造成管片的张开；②不均匀沉降诱发的剪切应力引发管片之间的错台变形^[23-24]。戴宏伟等^[6]、李俊昱等^[11]采用Euler-Bernoulli梁分别计算了隧道和管线的纵向变形,但Euler-Bernoulli梁只能考虑弯曲变形,无法得到管片之间的错台量大小,因此本文采用Timoshenko梁来模拟盾构隧道。

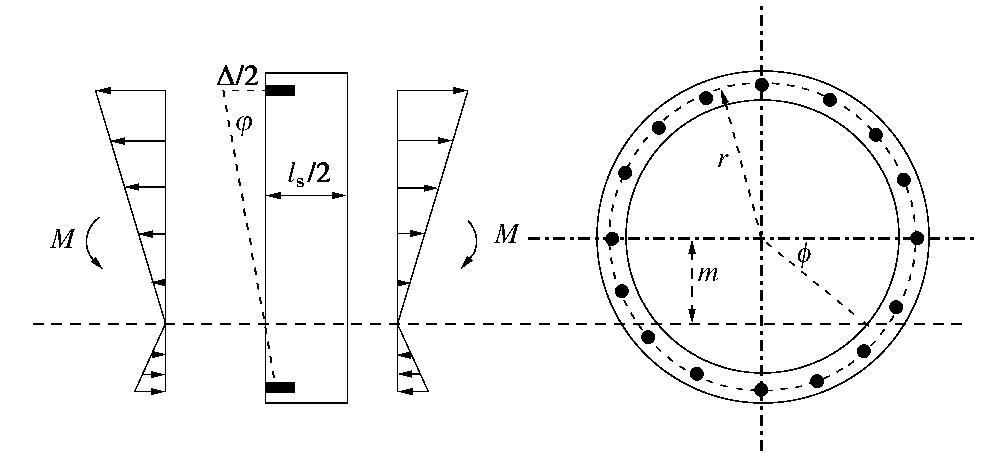
为了考虑管片之间接头的存在引起隧道纵向刚度的衰减,大量学者进行了研究^[25-26],其中日本学者Shiba提出的刚度等效方法在工程中得到了大量应用,本文同样也采用该方法。图3为隧道变形示意图,通过变形协调条件,可以得到隧道等效抗弯刚度、等效抗剪刚度、张开量和错台量。

图 3 管片受力和变形示意图

Figure 3. Deformation and stress of linings

下载: 全尺寸图片幻灯片

a）等效抗弯刚度和张开量

\begin{array}{l} ϕ + \cot ϕ = π (0.5 + \frac{N k_{b} l_{s}}{E_{c} A_{c}}), \\ φ = \frac{l_{s}}{E_{c} I_{c}} \frac{\cos ϕ + (ϕ + π / 2) \sin ϕ}{\cos^{3} ϕ} M, \\ E I_{eq} = \frac{\cos^{3} ϕ}{\cos ϕ + (ϕ + π / 2) \sin ϕ} E_{c} I_{c} 。 \end{array}}

(8)

式中,N为纵向螺栓的数量, $k_{b}$ 为螺栓的刚度： $k_{b} =$ $E_{b} A_{b} / l_{b}$ , $l_{s}$ 和 $l_{b}$ 分别为管片和螺栓的长度, $E_{c}$ 和 $I_{c}$ 分别为管片的弹性模量和隧道的惯性矩。

由弯矩引起管片之间最大张开量可以表示为

Δ = φ (r + m) = \frac{M}{E I_{eq}} (r + r \sin ϕ) l_{b} 。

(9)

b）等效剪切刚度和错台量

基于Timoshenko梁理论和变形协调条件,隧道的等效剪切刚度可以表示为

G_{e q} = ζ \frac{l_{s}}{\frac{l_{b}}{N κ_{b} G_{b} A_{b}} + \frac{l_{s}}{κ_{c} G_{c} A_{c}}},

(10)

式中 $ζ$ 为考虑影响隧道刚度相关因素的修正参数,一般取1； $κ_{b}$ 和 $κ_{c}$ 为Timoshenko梁和管片的剪切刚度修正系数,分别取0.9和0.5； $G_{b}$ 和 $G_{c}$ 分别为螺栓和隧道的剪切模量； $A_{b}$ 和 $A_{c}$ 分别为螺栓和隧道的横截面积。

由剪切引起管片之间的错台量可以表示为

δ = l_{s} \frac{Q}{G_{eq}} 。

(11)

（3）隧道变形计算模型

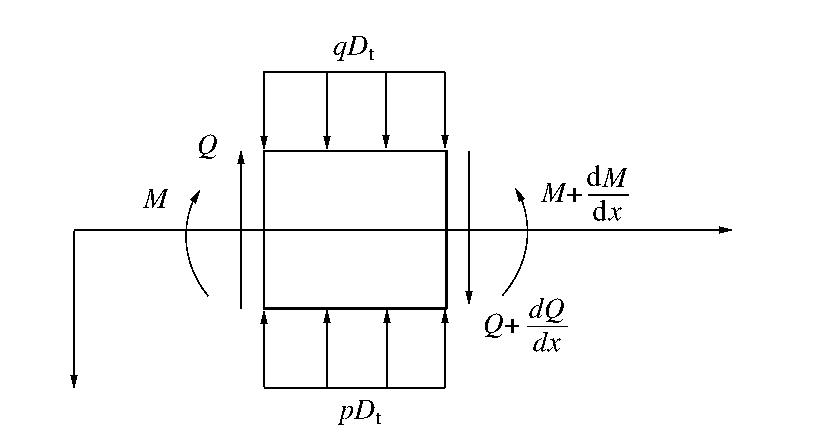
为简化计算,假设地表荷载作用前隧道变形已经稳定、隧道与周围土体始终保持接触,并且不考虑土体固结、蠕变以及荷载随时间的变化。取隧道微元体单元进行受力分析（如图4所示）,可以得到如下两个平衡方程：

图 4 隧道单元受力分析图

Figure 4. Force analysis of element

下载: 全尺寸图片幻灯片

Q + p D_{t} d x = q D_{t} d x + Q + d Q / d x （ 力 平 衡 方 程 ）,

(12a)

\begin{matrix} - M - Q d x - p D_{t} d x d x / 2 + q D_{t} d x d x / 2 + M + d M / d x = 0 \\ （ 力 矩 平 衡 方 程 ） 。 \end{matrix}

(12b)

式中 $Q$ 和 $M$ 分别为作用在隧道上的剪力和弯矩； $q$ 为堆载引起的附加应力； $D_{t}$ 为隧道外径； $p$ 为地基反力,根据Winkler地基模型, $p = k w (x)$ , $k$ 为地基反力系数,由式（7）确定, $w (x)$ 为堆载引起的隧道沉降。

根据Timoshenko梁理论,内力与变形之间的关系为

M = - E I_{eq} \frac{d θ}{d x}, Q = G_{eq} (\frac{d w}{d x} - θ),

(13)

式中, $θ$ 为梁截面中性面的转动角度。

联立式（12a）,（12b）,（13）,可以得到地表竖向荷载下盾构隧道竖向位移w(x)的微分控制方程：

\frac{d^{4} w (x)}{d x^{4}} + α \frac{d^{2} w (x)}{d x^{2}} + β w (x) = α_{1} \frac{d^{2} q (x)}{d x^{2}} + β_{1} q (x),

(14)

式中, $α = - \frac{k D_{t}}{G_{eq}}$ , $β = \frac{k D_{t}}{E I_{eq}}$ , $α_{1} = - \frac{D_{t}}{G_{eq}}$ , $β_{1} = \frac{D_{t}}{E I_{eq}}$ 。

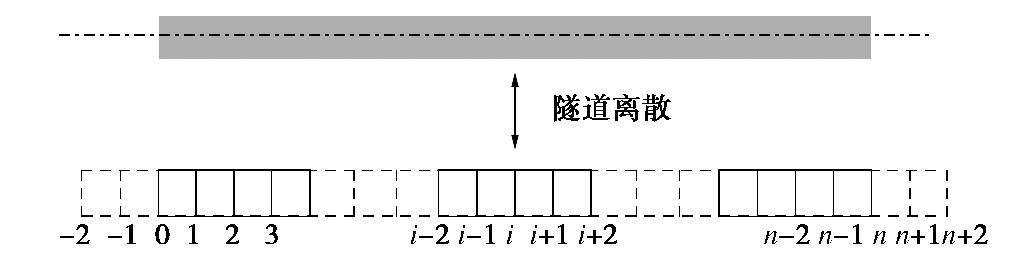
式（14）为4阶常微分方程,很难直接得到其显式解析解,故采用有限差分法将微分方程转换为代数形式的差分方程,通过编程求其数值解。先将隧道离散成n+5个微单元体,每个单元体的长度为l,如图5所示,-2,-1,n+1和n+2均为虚节点。假设隧道两端均自由,即无弯矩和剪力作用。因此,对于0节点和n节点,分别满足边界条件： $Q_{0} = Q_{n} = 0$ , $M_{0} =$ $M_{n} = 0$ 。根据差分原理,结合边界条件,式（14）可以改写为以挠度w(x)为未知数的矩阵表达式：

图 5 隧道离散分析

Figure 5. Discretization of tunnel

下载: 全尺寸图片幻灯片

K W = D S,

(15)

式中, $W = {[w_{0} w_{1} \dots w_{n - 1} w_{n}]}^{T}$ , $S =$ ${[q_{0} q_{1} \dots q_{n - 1} q_{n}]}^{T}$ ,可以通过式（5）求得,K和D的表示形式见附录。求解式（15）就可以得到地表荷载作用下隧道的纵向变形,然后联立式（9）～（13）,进一步可以得到隧道承受的弯矩、剪力、张开量和错台量。

1.3 算例验证

（1）与Boussinesq解比较

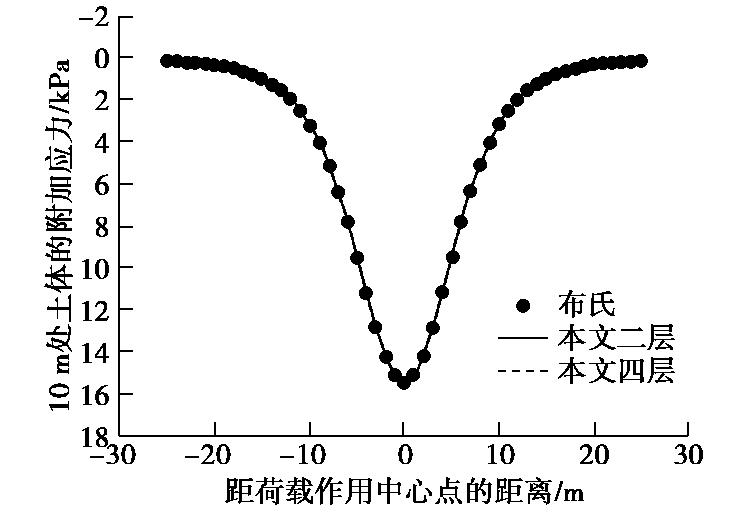
基于式（5）,采用双重Fourier逆变换和高斯积分法,可以得到分层地基中地表堆载引起的附加应力,通过与经典的Boussinesq解进行对比,来验证分层地基应力计算模型以及数值变换的正确性。假设地表作用100 kN的荷载,荷载作用范围为4×10 m,地基土为弹性半空间无限体,弹性模量为10 MPa,泊松比为0.33。分别采用Boussinesq解和本文解（其中土体分层数取为2层和4层）计算10 m处的附加应力,计算结果如图6所示,对比结果表明,本文计算结果与Boussinesq解基本一致,从而验证了本文分层土体附加应力计算模型的可靠性。

图 6 附加应力计算结果对比

Figure 6. Comparison of additional stress

下载: 全尺寸图片幻灯片

（2）与已有文献比较

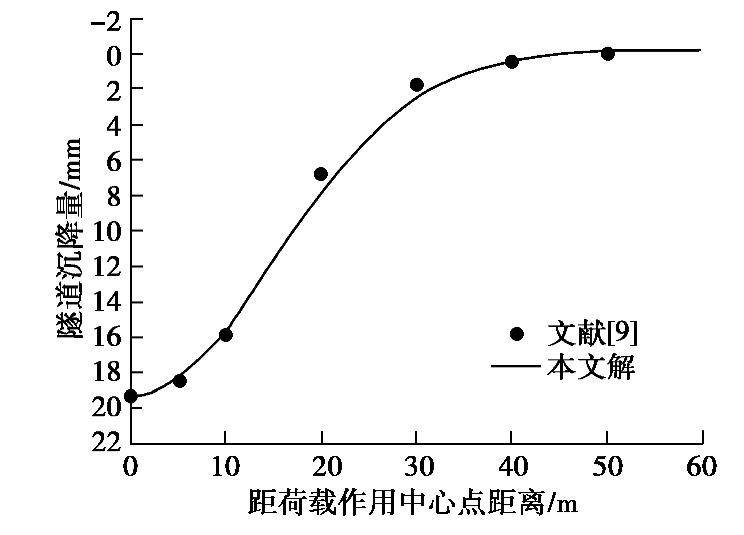
文献[9]以上海典型隧道为研究背景,分析了均质土体中地表堆载对隧道纵向变形的影响。采用本文的计算结果与文献的结果如图7所示,进一步验证了本文计算模型的正确性。

图 7 均质地基中堆载引起的隧道沉降

Figure 7. Comparison of settlement

下载: 全尺寸图片幻灯片

2. 影响参数分析

假定在隧道轴线正上方地表进行工程堆土,堆土重度为18 kN/m³,堆土高度为4 m,地表附加荷载作用范围为2a×2b=20 m×40 m,隧道轴线埋深为15 m。隧道为上海典型地铁隧道,管片内外径分别为5.5 m和6.2 m,环宽为1.2 m,弹性模量为3.45×10⁷ kPa。螺栓为17个,直径为0.03 m,长度为0.4 m,弹性模量为2.06×10⁸ kPa。在下面分析中,若无特别说明,隧道所取参数不变。

2.1 上覆土体模量

为了便于分析,假设第一层层厚10 m,弹性模量变化范围为5～40 MPa,泊松比为0.35,第二层为半无限空间体,弹性模量为10 MPa,泊松比为0.35。

隧道正上方堆载情况下,上覆土体模量对隧道纵向变形影响如图8（a）所示。隧道竖向沉降最大值出现在荷载作用中心处,随着上覆土体模量越大隧道纵向变形越小；当上覆土体模量从5 MPa增大到40 MPa时,隧道最大沉降从16 mm减小为12 mm,最大沉降幅度减小了25%。这主要是因为上覆土体模量越大,土体强度越高,应力扩散效应越明显,作用在隧道上的附加应力也就越小,从而引起隧道的沉降量也就越小。距堆载中心40 m附近,隧道沉降几乎为零,因此隧道沉降槽宽度约为80 m,是荷载作用宽度（沿隧道轴线方向）的4倍,且沉降槽宽度几乎不受上覆土体模量的影响。

图 8 上覆土体模量对隧道内力和变形的影响

Figure 8. Effects of modulus of overlying soil on tunnel deformation and internal forces

下载: 全尺寸图片幻灯片

图8（b）,（c）分别为隧道所受弯矩和张开量随上覆土层模量的变化情况。由图可知,堆载作用下隧道弯矩和张开量沿隧道纵向的分布一致,最大值均出现在荷载作用中心点处,此处即为隧道最危险截面,隧道管片可能因为过大的压应力或拉应力导致破损或产生裂缝,从而引发隧道渗水,影响隧道安全运营。地表堆载下,隧道受到的最大剪力和错台量出现在荷载作用边缘处,如图8（d）,（e）所示,这表明在这些隧道截面处,螺栓承受的剪应力最大,因而最容易发生破坏。

综上,在堆载中心处和边缘处,隧道会因承受较大的弯矩和剪力而出现较大的张开量和错台量,情况严重时甚至导致隧道出现道床脱落管片混凝土挤碎、螺栓剪断、渗漏水以及纵缝张开等^[1]病害,影响隧道的安全运营。所以,一旦隧道正上方出现堆载,需要加强这些隧道截面的监测工作或提前采取保护措施,预防隧道病害的产生。

2.2 下卧土体模量

为了便于分析,假设第一层层厚20 m,弹性模量为10 MPa,泊松比为0.35,第二层为半无限空间体,弹性模量变化范围为5～40 MPa,泊松比为0.35。

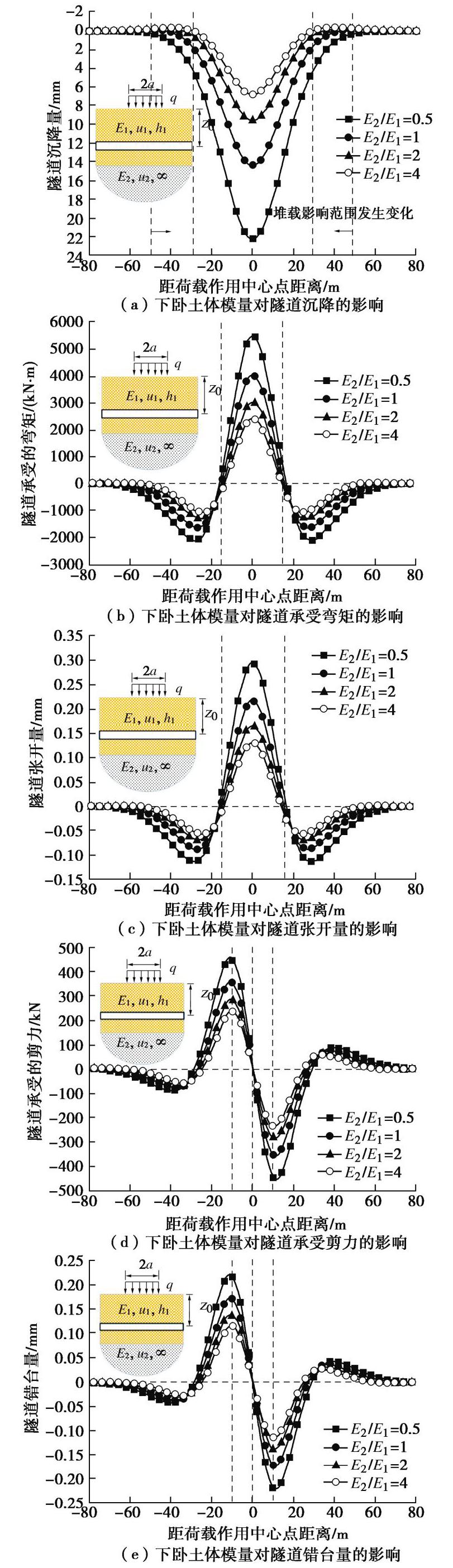
隧道正上方地表堆载作用下,隧道下卧土体模量对隧道内力和变形的影响如图9所示。由图9（a）可知,下卧土体模量越大,地表荷载作用下隧道沉降越小；当下卧土体模量从5 MPa增大到40 MPa时,隧道最大沉降从22 mm减小为7 mm,最大沉降幅度减小了68%。这主要是因为下卧土体模量越大,土体刚度也就越大,对上覆土体的约束作用也随之增加；当下卧土体的模量趋于无穷大时,下卧土层可以等效为刚性边界,即上覆土体底部的竖向位移完全被约束,此种情况下隧道的纵向变形完全取决于上层土体的性质。此外,与图9（a）比较,隧道沉降范围随着下卧土体模量的增大明显缩小,从5倍加载宽度减小为3倍。

图 9 下卧土体模量对隧道内力和变形的影响

Figure 9. Effects of modulus of underlying soil on tunnel deformation and internal forces

下载: 全尺寸图片幻灯片

下卧土体模量对隧道承受的弯矩、张开量、剪力以及错台量的影响分别如图9（b）～（e）所示,随着下卧土体模量的增加,隧道内力和变形随之减小,变化趋势与上层土体一致,此处不再赘述。

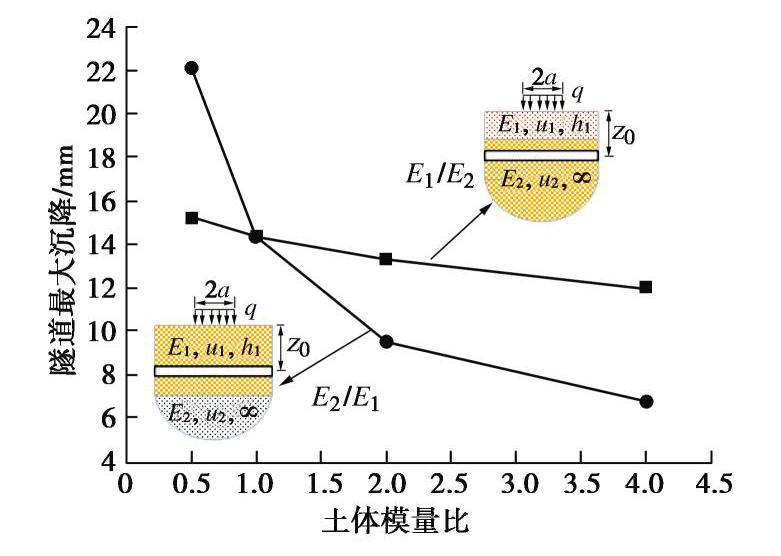
两层土体情况下,隧道最大沉降随土体模量比变化的计算结果如图10所示。由图10可知,在地表堆载作用下,无论是上覆土体模量增加,还是下卧土体模量增加,隧道竖向最大沉降均会降低,相比而言下卧土层的影响更为明显,说明下卧土层控制隧道沉降的效果要优于硬表层地基的情况。另一方面,当下卧土层模量小于隧道所处土层的模量时（即下卧软土层）,隧道沉降急剧增大。因此,若隧道下卧软土层,需要引起重视,不宜进行堆土工程,避免隧道因堆载出现过大的变形。

图 10 最大沉降随土体模量比的变化趋势

Figure 10. Effects of relative soil modulus on maximum tunnel settlement

下载: 全尺寸图片幻灯片

3. 结论

地表堆载会改变隧道原有的平衡状态,引起隧道结构产生过大变形,诱发一系列的隧道病害。基于层状弹性半空间理论,本文建立了层状地基中地表堆载对既有隧道影响的弹性分析方法,分析了土体分层特性对隧道结构响应的影响,得到以下3点结论。

（1）本文采用弹性层状半空间地基模型,建立了能够考虑非均质土体条件的地表大面积荷载对临近既有隧道影响的弹性分析方法,并编写了层状地基中隧道性状的分析程序,方便求解出地表堆载作用下土体特性对既有盾构隧道的内力和变形响应。通过与已有文献数据的对比,验证了本文模型的合理性。

（2）本文方法具有较强的通用性,不仅可以解答均质地基的情况,还可以解答非均质地基的情况,继而可以反映土体分层特性对隧道的影响。对上海典型地铁隧道性状进行参数分析,结果表明上覆土层和下卧土层的弹性模量对隧道沉降和受力具有较为明显的影响,其中增大下卧层土体弹性模量可以显著减小隧道沉降。

（3）当隧道下卧软土层时,地表堆载作用下隧道更容易发生变形,为了保证隧道的安全运营,应该严格评估隧道地表堆载的影响。

此外,限于篇幅,本文仅考虑了隧道正上方大面积堆载引发的隧道纵向变形响应,未涉及到隧道堆载（尤其是偏载）对隧道侧向变形的影响,因此在后续的研究中也可以进行具体分析。

附录

图 1 层状地基示意图

Figure 1. Cross section of multi-layered soils

下载: 全尺寸图片幻灯片

图 2 偏心堆载

Figure 2. Eccentric surcharge

下载: 全尺寸图片幻灯片

图 3 管片受力和变形示意图

Figure 3. Deformation and stress of linings

下载: 全尺寸图片幻灯片

图 4 隧道单元受力分析图

Figure 4. Force analysis of element

下载: 全尺寸图片幻灯片

图 5 隧道离散分析

Figure 5. Discretization of tunnel

下载: 全尺寸图片幻灯片

图 6 附加应力计算结果对比

Figure 6. Comparison of additional stress

下载: 全尺寸图片幻灯片

图 7 均质地基中堆载引起的隧道沉降

Figure 7. Comparison of settlement

下载: 全尺寸图片幻灯片

图 8 上覆土体模量对隧道内力和变形的影响

Figure 8. Effects of modulus of overlying soil on tunnel deformation and internal forces

下载: 全尺寸图片幻灯片

图 9 下卧土体模量对隧道内力和变形的影响

Figure 9. Effects of modulus of underlying soil on tunnel deformation and internal forces

下载: 全尺寸图片幻灯片

图 10 最大沉降随土体模量比的变化趋势

Figure 10. Effects of relative soil modulus on maximum tunnel settlement

下载: 全尺寸图片幻灯片

参考文献(26)

[1]	邵华, 黄宏伟, 张东明, 等. 突发堆载引起软土地铁盾构隧道大变形整治研究[J]. 岩土工程学报, 2016, 38(6): 1036-1043. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201606009.htm SHAO Hua, HUANG Hong-wei, ZHANG Dong-ming, et al. Case study on repair work for excessively deformed shield tunnel under accidental surface surcharge in soft clay[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 1036-1043. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201606009.htm
[2]	范垚垚, 郭晓航, 邓指军, 等. 正上方加卸载对盾构隧道变形的影响分析[J]. 施工技术, 2014, 43(7): 107-109. https://www.cnki.com.cn/Article/CJFDTOTAL-SGJS201407032.htm FAN Yao-yao, GUO Xiao-hang, DENG Zhi-jun, et al. Deformation analysis of shield tunnel with loading and unloading above[J]. Construction Technology, 2014, 43(7): 107-109. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SGJS201407032.htm
[3]	黄大维, 周顺华, 赖国泉, 等. 地表超载作用下盾构隧道劣化机理与特性[J]. 岩土工程学报, 2017, 39(7): 1173-1181. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201707003.htm HUANG Da-wei, ZHOU Shun-hua, LAI Guo-quan, et al. Mechanisms and characteristics for deterioration of shield tunnels under surface surcharge[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(7): 1173-1181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201707003.htm
[4]	HUANG H, ZHANG D. Resilience analysis of shield tunnel lining under extreme surcharge: characterization and field application[J]. Tunnelling and Underground Space Technology, 2016, 51: 301-312. doi: 10.1016/j.tust.2015.10.044
[5]	王如路, 张冬梅. 超载作用下软土盾构隧道横向变形机理及控制指标研究[J]. 岩土工程学报, 2013, 35(6): 1092-1101. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201306016.htm WANG Ru-lu, ZHANG Dong-mei. Mechanism of transverse deformation and assessment index for shield tunnels in soft clay under surface surcharge[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1092-1101. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201306016.htm
[6]	戴宏伟, 陈仁朋, 陈云敏. 地面新施工荷载对临近地铁隧道纵向变形的影响分析研究[J]. 岩土工程学报, 2006. 28(3): 312-316. doi: 10.3321/j.issn:1000-4548.2006.03.006 DAI Hong-wei, CHEN Ren-peng, CHEN Yun-min. Study on effect of construction loads on longitudinal deformation of adjacent metro tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 312-316. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.03.006
[7]	魏新江, 洪文强, 魏纲, 等. 堆载引起临近地铁隧道的转动与错台变形计算[J]. 岩石力学与工程学报, 2018, 37(5): 1281-1289. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201805022.htm WEI Xin-jiang, HONG Wen-qiang, WEI Gang, et al. Rotation and shearing dislocation deformation of subway tunnels due to adjacent ground stack load[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(5): 1281-1289. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201805022.htm
[8]	魏纲, 俞国骅, 洪文强. 地面堆载引起下卧盾构隧道剪切错台变形计算研究[J]. 中南大学学报(自然科学版), 2018, 49(7): 1775-1783. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201807026.htm WEI Gang, YU Guo-hua, HONG Wen-qiang. Study on calculation of shield tunnel shearing dislocation platform deformation due to adjacent ground stacked load[J]. Journal of Central South University (Science and Technology), 2018, 37(5): 1281-1289. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201807026.htm
[9]	康成, 梅国雄, 梁荣柱, 等. 地表临时堆载诱发下既有盾构隧道纵向变形分析[J]. 岩土力学, 2018, 39(12): 4605-4616. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201812037.htm KANG Cheng, MEI Guo-xiong, LIANG Rong-zhu, et al. Analysis on the longitudinal deformation of existing shield tunnel induced by temporary surface surcharge[J]. Rock and Soil Mechanics, 2018, 39(12): 4605-4616. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201812037.htm
[10]	高继锦, 黄彪, 张威, 等. 地面堆载条件下交叉穿越隧道的竖向位移计算方法研究[J]. 隧道建设, 2018, 38(5): 818-823. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201805017.htm GAO Ji-jin, HUANG Biao, ZHANG Wei, et al. Study of calculation method for vertical displacement of crossed tunnels under surface surcharge loading[J]. Tunnel Construction, 2018, 38(5): 818-823. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201805017.htm
[11]	李俊昱, 钱建固, 茹治敏, 等. 高填方对分层地基地埋管线影响的三维分析方法[J]. 岩土工程学报, 2015, 37(增刊2): 65-69. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S2015.htm LI Jun-yu, QIAN Jian-gu, RU Zhi-min, et al. Three-dimensional method for response of embedded pipelines to earthfill load[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S2): 65-69. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S2015.htm
[12]	张明告, 周顺华, 黄大维, 等. 地表超载对地铁盾构隧道的影响分析[J]. 岩土力学, 2016, 37(8): 2271-2278. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201608019.htm ZHANG Ming-gao, ZHOU Shun-hua, HUANG Da-wei, et al. Analysis of influence of surface surcharge on subway shield tunnel under[J]. Rock and Soil Mechanics, 2016, 37(8): 2271-2278. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201608019.htm
[13]	ZHANG Z, HUANG M, ZHANG M. Deformation analysis of tunnel excavation below existing pipelines in multi-layered soils based on displacement controlled coupling numerical method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(11): 1440-1460.
[14]	张治国, 黄茂松, 王卫东. 层状地基中隧道开挖对临近既有隧道的影响分析[J]. 岩土工程学报, 2009, 31(4): 600-608. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200904023.htm ZHANG Zhi-guo, HUANG Mao-song, WANG Wei-dong. Analysis on response of existing tunnels due to adjacent tunneling in multi-layered soils[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 600-608. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200904023.htm
[15]	钟阳. 多层弹性半空间问题解的精确刚度矩阵法[J]. 应用力学学报, 2008, 25(2): 316-319. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX200802031.htm ZHONG Yang. Explicit solution of multilayered elastic half space by exact stifness matrix method[J]. Chinese Journal of Applied Mechanics, 2008, 25(2): 316-319. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX200802031.htm
[16]	艾智勇, 吴超. 三维直角坐标系下分层地基的传递矩阵解[J]. 重庆建筑大学学报, 2008, 30(2): 43-46. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN200802008.htm AI Zhi-yong, WU Chao. Transfer matrix solutions for multi-layered soils in rectangular coordinate system[J]. Journal of Chongqing Jianzhu University, 2008, 30(2): 43-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN200802008.htm
[17]	HUANG M, ZHANG C, LI Z. A simplified analysis method for the influence of tunneling on grouped piles[J]. Tunnelling and Underground Space Technology, 2009, 24(4): 410-422.
[18]	钟阳, 殷建华. 弹性层状体的求解方法[M]. 北京: 科学出版社, 2007. ZHONG Yang, YIN Jian-hua. Methods for Layered Elastomer[M]. Beijing: Science Press, 2007. (in Chinese)
[19]	BOOKER J, SMALL J. Finite layer analysis of consolidation I[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1982(6): 151-171.
[20]	YU J, ZHANG C, HUANG M. Soil-pipe interaction due to tunnelling: assessment of Winkler modulus for underground pipelines[J]. Computers and Geotechnics, 2013, 50: 17-28.
[21]	LIANG R, XIA T, HUANG M, et al. Simplified analytical method for evaluating the effects of adjacent excavation on shield tunnel considering the shearing effect[J]. Computers and Geotechnics, 2017, 81: 167-187.
[22]	LIANG R, WU W, YU F, et al. Simplified method for evaluating shield tunnel deformation due to adjacent excavation[J]. Tunnelling and Underground Space Technology, 2018, 71: 94-105.
[23]	SHEN S, WU H, CUI Y, et al. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai[J]. Tunnelling and Underground Space Technology, 2014, 40: 309-323.
[24]	DI H, ZHOU S, XIAO J, et al. Investigation of the long-term settlement of a cut-and-cover metro tunnel in a soft deposit[J]. Engineering Geology, 2016, 204: 33-40.
[25]	叶飞, 何川, 朱合华, 等. 考虑横向性能的盾构隧道纵向等效刚度分析[J]. 岩土工程学报, 2011, 33(12): 1870-1876. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201112010.htm YE Fei, HE Chuan, ZHU He-hua, et al. Longitudinal equivalent rigidity analysis of shield tunnel considering transverse characteristics[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1870-1876. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201112010.htm
[26]	叶飞, 杨鹏博, 毛家骅, 等. 基于模型试验的盾构隧道纵向刚度分析[J]. 岩土工程学报, 2015, 37(1): 83-90. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201501011.htm YE Fei, YANG Peng-bo, MAO Jia-hua, et al. Longitudinal rigidity of shield tunnels based on model tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 83-90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201501011.htm

施引文献(38)

期刊类型引用(28)

1.	曹仲科. 盾构隧道渗漏水原因及防治探究. 甘肃科技. 2024(08): 9-12 . 百度学术
2.	项阳，赵昊磊. 上方堆载引起既有隧道变形效应数值试验分析. 安徽建筑. 2024(10): 162-163 . 百度学术
3.	王虎，叶胜，罗天霖，宋敦安，李栋. 深厚软土区地表附加荷载对顶管隧道变形的影响分析. 现代隧道技术. 2024(S1): 1011-1017 . 百度学术
4.	汤友生，佘剑波，鲜少华. 地面堆载对输水隧道变形及保护措施研究. 工程建设. 2024(12): 50-56 . 百度学术
5.	王如路，袁强，梁发云，王鲁杰. 道路填土引发软土地铁盾构隧道变形案例及整治技术. 岩土工程学报. 2023(01): 112-121 . 本站查看
6.	李创，陈德刚，周明，张素磊，张坤鹏. 堆载作用下土岩复合地层隧道坍塌特征及演变规律研究. 青岛理工大学学报. 2023(01): 1-10 . 百度学术
7.	刘喜东. 宁波软土地区双线隧道上穿施工对既有隧道变形性状的影响. 结构工程师. 2023(01): 161-168 . 百度学术
8.	张芳，王露露，朱云桂，黄磊，禹姿含，丁爽. 地面堆载作用下盾构隧道结构变形分析. 科学技术与工程. 2023(08): 3474-3481 . 百度学术
9.	梁荣柱，王理想，李忠超，康成，高坤，柯宅邦. 地表堆载对既有盾构隧道纵向变形影响. 建筑科学与工程学报. 2023(03): 130-141 . 百度学术
10.	王露露，丁爽，黄磊，王亚哲，赵怡琳，张芳. 地面堆载作用下既有隧道的工作状态. 科学技术与工程. 2023(13): 5764-5769 . 百度学术
11.	黄大维，徐长节，罗文俊，姜浩，刘家璇，李庆. 土压平衡盾构施工模块化分步缩尺模型试验设计与应用. 交通运输工程学报. 2023(04): 248-257 . 百度学术
12.	曾超峰，蔡钢，朱龙，张祖浩，陈宏波，薛秀丽，龙四春，罗桂军. 考虑既有地铁车站阻隔效应的基坑抽水致沉模型试验研究. 岩石力学与工程学报. 2023(10): 2566-2577 . 百度学术
13.	曹小林，周凤玺，戴国亮. 水平荷载作用下饱和土与单桩的相互作用动力响应分析. 岩土工程学报. 2023(S2): 73-78 . 本站查看
14.	赵星星. 盾构隧道下穿九圩港河纵向稳定性研究. 建筑机械化. 2022(04): 49-52 . 百度学术
15.	刘谨豪，严远忠，张琪，卞荣，贺雷，叶冠林. 地面堆载对既有隧道影响离心试验和数值分析. 上海交通大学学报. 2022(07): 886-896 . 百度学术
16.	魏纲，张书鸣，余剑英，丁智，崔允亮. 地面堆载对盾构隧道围压影响的模型试验与理论分析. 岩土工程学报. 2022(10): 1789-1798 . 本站查看
17.	魏纲，张书鸣. 地面堆载对临近地铁盾构隧道影响的研究综述. 低温建筑技术. 2021(01): 92-97 . 百度学术
18.	梁发云，方衍其，袁强，李家平. 软、硬地层中局部堆载对隧道横向变形影响的试验研究. 同济大学学报(自然科学版). 2021(03): 322-331+430 . 百度学术
19.	刘谨豪，严远忠，张琪. 地面超载对地下管道影响的HSS模型数值模拟. 徐州工程学院学报(自然科学版). 2021(01): 38-45 . 百度学术
20.	江杰，龙逸航，邢轩伟，王顺苇. 富水圆砾地层盾构下穿既有地铁隧道掘进参数研究. 铁道科学与工程学报. 2021(07): 1828-1836 . 百度学术
21.	刘元鹏，黄志坚. 泥沙搬运对盾构掌子面稳定性影响研究. 低温建筑技术. 2021(08): 123-126+130 . 百度学术
22.	王明俊，王朋，柯树炜. 基础沉降对钢型井架承载力及稳定性的影响规律研究. 城市住宅. 2021(09): 193-195+198 . 百度学术
23.	颉永斌，董建华. 断层破碎带内隧道纵向受荷特征和变形分析. 中国公路学报. 2021(11): 211-224 . 百度学术
24.	王敏，甘晓露，杜巍，俞建霖，龚晓南. 考虑土体刚度衰减的地面堆载对既有隧道影响. 地下空间与工程学报. 2021(06): 1965-1971+1979 . 百度学术
25.	李磊. 地铁隧道纵向变形影响因素与控制对策研究. 工程技术研究. 2020(04): 170-171 . 百度学术
26.	王彦峰，刘庭金，余克鹏，郭金根，梁爱武. 地表超卸载对高压电缆盾构隧道变形影响数值分析. 广东土木与建筑. 2020(07): 46-49+54 . 百度学术
27.	陈家康. 基坑开挖和堆载对邻近建筑物基础的影响模拟. 山西建筑. 2020(21): 57-60 . 百度学术
28.	杨威，方衍其，梁发云. 大规模群桩基础对邻近轨道交通影响的简化分析方法. 结构工程师. 2020(05): 145-152 . 百度学术

其他类型引用(10)

资源附件(0)

图(10)

计量

文章访问数: 427
HTML全文浏览量: 32
PDF下载量: 327
被引次数: 38

0. 引言
1. 计算模型
1.1 直角坐标系下弹性层状半空间体系基本解
1.2 地表荷载作用下盾构隧道变形计算
1.3 算例验证
2. 影响参数分析
2.1 上覆土体模量
2.2 下卧土体模量
3. 结论
附录

堆载作用下土体分层特性对地铁隧道纵向变形的影响研究 English Version

作者简介: 梁发云（1976— ）,男,博士,教授,主要从事土力学与基础工程的教学科研工作。E-mail：fyliang@tongji.edu.cn

计量

出版历程